高屋建瓴应悟道 柳暗花明又一解——以2018年浙江卷17题为例

广东省广州市从化区第四中学 黄 强

数学学科核心素养是数学课程目标的集中体现，是在数学学习和应用的过程中逐步形成和发展的。数学学科核心素养的本质反映了数学思维品质，其关键是能从数学的角度思考问题。 发散性思维又称辐射思维，是根据已有的信息，从不同的角度思考，寻求多样性答案的思维活动。在解决问题中表现了根据已知条件，能从不同的角度进行思考，探究多种不同的解决办法的思维活动，其具有思考角度多变、解决方法灵活的特点，是思维灵活性的表现。在解题活动中，教师常用典例多解的教学形式来培养学生的发散性思维。笔者认为引导学生不囿于一个角度或一种思路去探究解法，关键是不但要渗透数学思想，更要揭示数学思想在思考过程中的运用，从而使学生认识到思考角度的多变源于数学思想，解决方法的灵活生于数学思想。 因此，为了培养学生的发散性思维能力，通过典例多解和数学思想的揭示，这不仅促进学生知识网络的形成，而且更重要的是促使学生对数学思想的感悟，提高解题能力和发散思维能力，提升数学思维品质。本文以2018年浙江高考的一道试题为例，以期抛砖引玉。

例题：（2018年浙江卷17题）已知点P(0,1)，椭圆上两点A，B满足则当m=_________时，点B横坐标的绝对值最大。

一、运用方程思想探解

运用方程思想，就是通过分析问题中已知与未知的等量关系，建立方程（组），运用方程的性质分析转化问题，从而使问题得到解决的思维过程。相应方程思想下的常见方法有点差法、韦达定理、判别式等等。揭示方程思想在解题中的运用，使学生认识到解法并非无中生有，其根源在于数学思想给我们提供一个思考角度。

因为A，B点在椭圆上，所以两式相减有代入椭圆方程并化简得：m＞1，易知当m=5时的最大值为4，即

评析：本解法运用方程思想作为思考角度。为了探求等量关系，先“固定m”， 再通过平面共线向量抓住关键点B，这样处理不但减少了变量数对思维的影响，更重要的是突出了关键的未知量，即减少是为了突出。由两个动点A，B在椭圆上这个几何特征建立方程尤为重要，其数学思想是由形转数，从而建立了点B的坐标与m的等量关系，然后把坐标的最值转化为二次函数最值问题。整个解决过程清晰明快，一气呵成！

运用直线的参数方程，也是解析几何常用的方法，其思维的关键包括：一是理解参数方程既表示直线方程，同时也表示点，是两者更抽象的形式；二是理解参数在问题中的几何意义。用参数方程表示点，其作用相当于减少变量数，同样，利用点在椭圆这个几何特征上建立方程，利用参数的几何意义和方程性质解决问题。

解法二：设直线AB的参数方程为其中t为参数，θ为直线AB的倾斜角。因为直线AB与椭圆相交，把直线AB的参数方程代入椭圆方程，得由韦达定理可知

二、运用函数思想探解

客观世界的事物是运动变化的，事物间既有联系，也有制约，这种关系在数学中以函数来刻画。运用函数思想探求问题的解决，其思维过程是通过挖掘变量间的关系构造函数，利用函数的性质解决问题。考虑到A，P，B三点共线，点P为定点，当直线AB绕点P旋转时，点B的坐标也随之变化，既然是动点，就需要知道按照什么规律运动，因此，挖掘点B的横坐标与直线AB斜率之间的函数关系为思考提供一个角度。

解法三：设直线AB的方程为y=kx+1，因为直线AB与椭圆相交两点，故联立方程并消元得由韦达定理可知：

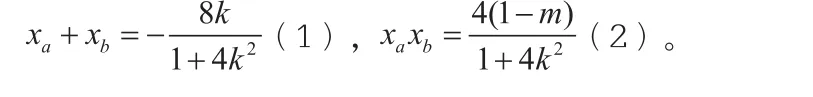
由椭圆对称性，不妨设xb＞0，由得xa=-2xb，代入（1）式，得由基本不等式得当且仅当xb取最大值2，此时由（2）式可知m=5。

评析：本解法综合运用数形结合、方程思想和函数思想，其思维过程通过形转数建立方程，利用方程性质挖掘函数关系，最后利用函数性质解决问题，但也看到如消去k，而不是消去m，虽然可以解决问题，但运算量陡增，学生就陷入复杂的运算中，因而抓牢函数思想，优化思考过程，从而解决问题。

三、运用变换思想探解

在人教版选修1-1的35页（或选修2-1的41页）中，设置了一个探究椭圆与圆之间关系的思考问题。通过探究，在伸缩变换下，有下列结论（在此证略）：（1）直线依然变换为直线；（2）椭圆变换为圆，圆变换为椭圆；（3）线段比不变；（4）直线与椭圆的交点对应直线与圆的交点。 把直线与椭圆的位置关系转换为直线与圆的位置关系。这是从变换几何思想的角度思考解法，其思维过程是把椭圆类比圆，把直线与椭圆问题转换为直线与圆的问题，利用圆的性质解决问题，这又为寻求新的解法提供了一个思考角度。

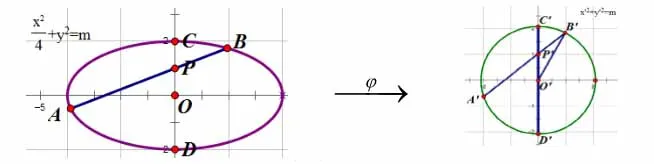
图1

设∠XO'B'=θ，点B'(x'b，y'b)，由余弦定理，得：化简得：

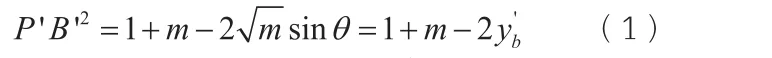
因为A'P'=2P'B'，并由相交弦定理C'P'·D'P'=P'B'·A'P'，得把（2）代入（1）并消去P'B'2，得即代入椭圆方程并化简，得易知当m=5时的最大值为4，即|xb|=2。

评析：本解法是通过对教材中的问题进行探究所获得的解法，因此重视教材中的探究问题，不但能培养学生的探究能力，往往还能获得新颖别致的解法，有利于拓宽学生思考角度，培养创新意识。

四、 运用特殊与一般探解

现实世界中，事物的特殊性中存在普遍性，个性中存在着共性，这在数学中就表现为特殊与一般的辩证关系，是重要的数学思想。其思维过程是以问题为起点，抛开其特殊性，探究更具一般形式的性质或规律，从而找到思考的角度，这对提升学生数学能力有积极的意义。在本题中，对于椭圆E1中的△ABO，有什么性质？能否对探究解法提供不同的思考角度？通过探究点P关于点A的对称点B的轨迹，如图2所示，我们有下面结论：

性质1：设椭圆曲线E1的方程为定点P(0,p)关于E1上的动点A的对称点B的轨迹为椭圆E2，椭圆方程为

略证：设点B(x,y)，因为点A(xa,ya)为线段PB的中点，所以有点A在E1上，代入E1的方程并化简，易得

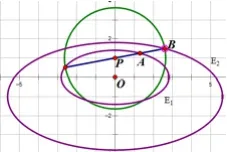
图2

而且通过探究，我们又发现以下性质：

证明：设直线AB的方程为y=kx+p，A(xA,yA)，B(xB,yB)，直线AB的方程与椭圆方程联立、消元并化简，得：

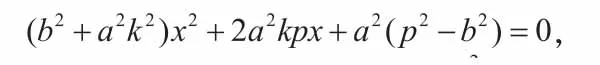
如图3所示，通过探究△ABO的AB边中点G的轨迹，有以下性质：

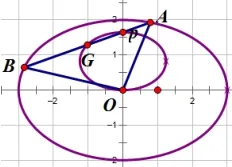
图3

证明：设直线AB的方程为y=kx+p，A(xA,yA)，B(xB,yB)，G(x,y)。联立直线AB方程与椭圆方程消元并化简，得（b2+a2k2）由韦达定理得x=两边平方并化简，得

从性质3可以获得下面推论：

利用性质1，我们可以得到下面解法：

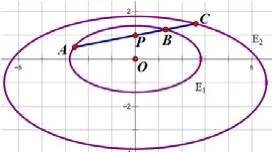
图4

利用性质2，我们又可以得到下面解法：

解法六：设A(xa，ya)，B(xb，yb)，由可知xa=-2xb，ya=-2yb+3。

直线AB,BO,AO的斜率分别为kAB、kOA和kOB，由性质2可知，即把xa=-2xb，ya=-2yb+3代入并化简，得代入椭圆方程并化简，得易知当m=5时的最大值为4，即|xb|=2。

数学学习离不开解题活动，在解题活动中，通过探究典例多解，可以培养学生发散思维，这是共识。如何培养学生找到解决问题的更多的思考角度，其关键在于揭示数学思想在解题中的运用，使学生对数学思想和方法有更深的感受。 如通过突出已知和未知，抓住几何特征建立方程，并运用方程的性质解决问题；如通过挖掘变量间的函数关系构造函数，并运用函数性质解决问题等等，但同时也要看到以下几点：（1）数学思想方法不但为解题找到思考角度，也自始至终贯穿整个解决过程；（2）在解题过程中往往由单一数学思想运用为开端，但思维过程又是多种思想方法的共同运用；（3）数学思想方法应该要揭示，因为数学思想是内隐，通过揭示其运用和提炼，使学生加深对数学思想的领悟，没有这一点，多解就变成一个技巧，不会真正内化学生的思维中。总之，跳出单纯的题海训练，鼓励独立思考，产生想法，大胆探索新思路，这不仅有助于学生进一步巩固、深化和拓展所学的知识，而且对提高自主学习能力和培育创新意识，提升科学探索素养，具有积极的促进作用。