“将军饮马”的前世今生
万红 杨文


摘要:利用“将军饮马”的数学问题模型,解决轴对称路径最短问题是数学问题解次中的一种重要思想,通过探究“将军饮马”模型的直线“前世”,拓展至曲线“今生”,试图妙用、巧用和活用思想,促进学生的思维多元发展和数学核心素养的培养.
关键词:将军饮马;对称;路径最短
1 提出问题
题目 已知F是双曲线等x2/4-y2/12 =1的左焦点,定点A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为_____.
此题是求两条线段之和最小值.如果仅仅从双曲线的定义和性质去解决问题,未免有些单一.为了与初中数学内容衔接,为了活用数学知识和培养拓展能力,解决该问题,可以追溯到初中学习的“将军饮马”模型.以下将从“将军饮马”模型的前世今生,详细阐述这类问题解决的关键.
2 解析“将军饮马”模型
“将军饮马”模型在古罗马时代就有了.传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?
从此,这个被称为“将军饮马”的问题广泛流传.
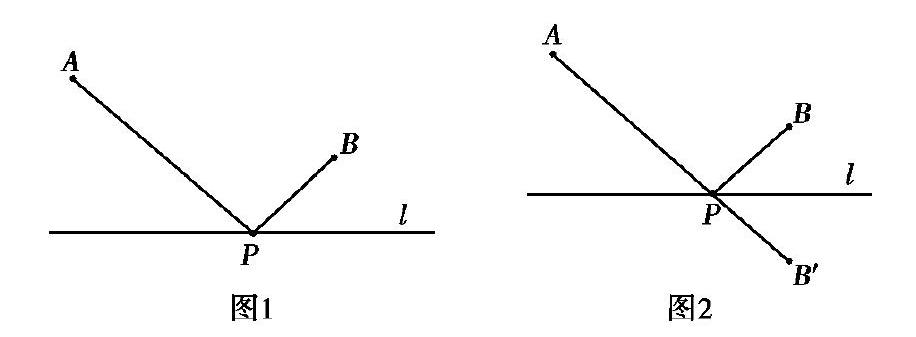
抽象为数学问题为:如图1,A,B两点为直线Z同侧的两点,点P为直线l上一动点,求点P位置使得AP+ PB最短.
解决该问题的做法为:如图2,作点B关于直线2对称的点B,连接AB交直线l于点P,则点P为所求点.
证明连接PB,由对称的性质可知PB= PB,则AP +PB =AP+ PB=AB.根据两点之间线段最短可得此时AP+ PB的长度最短.
3“将军饮马”模型在直线型条件的拓展
拓展1(一點两线)如图3,点A为∠BOC内部一点,M,N分别为OB,OC边上动点,求△AMN周长最小值.
拓展2(两点两线)如图4,点A、B为∠BOC内部两点,点M,N分别为OD,OC边上动点,求四边形ABMN周长最小值.
这两类拓展均为分别作两边的对称点,根据两点之间线段最短即可解决.(如图5,图6所示)
通过以上几种情况,可以发现,解决“将军饮马”模型的关键在“两点之间线段最短”.但是被我们忽略的问题是:对称的目的是什么?其实对称的目的是进行线段转化,在直线型的条件下,如果将点进行对称变换,则很容易将线段AP与PB从直线Z的同侧转化为异侧,通过“两点之间线段最短”即可证明.
4 解决上述问题
在提出的问题中,点A与点P是两个定点,点p为双曲线上一动点,符合“将军饮马”中“两点一线”的描述.但问题是:直线变成了曲线,对称还有用吗?其实此时再抓住对称这样的做法显然不能解决问题,但如果抓住解决“将军饮马”问题时对称目的是为了进行线段转化,将直线同侧两条线段转化为异侧两条线段,那问题就可以解决了.
6 小结
“将军饮马”模型常常以角、三角形、四边形、圆、坐标轴和抛物线为载体进行演绎,主要考查学生的综合实践能力、空间想象能力和判断推理能力[1].以上研究,一是促进初中数学知识与思想和高中数学知识与思想的衔接.许多初中知识在高中阶段发挥着极其重要的作用,在高中讲解时,由于没有联系初中已有的知识与经验,导致学生没有搞清楚问题的来龙去脉,使得学生不能在一个问题上举一反三;二是体现新课程实施的目标和要求在“经典”问题上开辟新的东西,找准“经典”问题生长的源泉和动力[2'.通过上述问题的发现、提出、分析与解决,希望对模型思想有更加深刻的认识.理解“知其然”,还要“知其所以然”和“知何由以知其所以然”[3].
参考文献:
[1]张进,唐芬,谈“将军饮马”问题—一以2015年全国各地中考试题为例[J].中国数学教育,2016(7 -8):110 -113.
[2]李克民.从经典模型的改造谈数学试题的命制——以“将军饮马”问题为例[J].教育研究与评论,2016(1):41 -45.
[3]荣贺,曲艺.与阿氏圆有关的广义将军饮马问题[J].数学通报,2018,57(8):48 -52.

