基于双边滤波-距离正则化水平集演化算法的甲状腺超声图像分割*

冉冬梅，严加勇，崔崤峣，于振坤

（1.上海理工大学医疗器械与食品学院，上海200093；2.上海健康医学院医疗器械学院，上海201318；3.中科院苏州生物医学工程技术研究所，苏州215163；4.南京同仁医院，南京211102）

1 引 言

近年来，甲状腺癌发病率在世界范围内逐年快速上升，早期发现、早期诊断是其治疗关键。目前，临床上广泛使用B超来实现对甲状腺相关疾病的筛查[1-2]。但是，传统的二维超声无法直接描述甲状腺病变的精准位置。因此，准确分割甲状腺具有重要临床意义。

受超声成像原理影响，甲状腺图像易产生斑点噪声，灰度对比度低、边缘模糊。传统的图像分割算法如边缘检测、阈值分割等[3-4]，都难以达到甲状腺分割要求。临床医师手动分割结果虽较为准确，但费时费力，分割结果往往还带有主观因素。

为实现甲状腺有效分割，国内外学者做了很多关于分割甲状腺超声图像的研究。Chang等[5]在2010年提出使用径向基函数（radial basis function，RBF）神经网络自动分割甲状腺的方案；2013年，Kaur等[6]分析了三种用于甲状腺分割的方法，即无边缘的活动轮廓、基于局部区域的活动轮廓和距离正则化水平集；同年，翟建敏等[7]提出采用手动绘图进行甲状腺微小结节的定位；2016年，Poudel等[8]提出先使用活动轮廓分割超声图像中的甲状腺，然后借助三维重建工具，获取甲状腺的三维模型。为提高分割精度，2017年Poudel等[9]通过添加均方误差比和直方图之间的相关性这两个区域相似性指标，将分割精度提高到86.7%。这些算法虽然能分割出甲状腺，但普遍计算复杂、耗时且分割效率低。

目前，图像分割领域一大研究热点是几何活动轮廓模型。根据处理图像的不同特征，分为基于图像区域[10-12]和边缘信息的几何活动轮廓模型[13-15]。其中，Li等[16]提出的基于边缘的无需初始化变分水平集方法受到广泛关注。该方法无需重新初始化，极大提高了分割效率，被称为距离正则化水平集演化，即DRLSE模型。

本研究针对甲状腺超声图像的特点，通过双边滤波来增强图像对比度、抑制噪声并保留图像边缘信息，降低原始图像复杂度。采用基于目标边界信息的变分水平集方法，即改进边缘指示函数的DRLSE模型，实现对甲状腺超声图像的分割。通过与使用另外两种边缘指示函数[16-17]的DRLSE模型的对比，本研究算法明显减少了迭代次数和运行时间。

2 本研究算法

2.1 BF模型

BF是一种非线性滤波器，最早由 Tomasi[18]提出，该滤波器可以在滤除噪声的同时，保留图像的边缘的信息，降低了图像的复杂度。BF是采用基于高斯分布加权平均的方法，用周边像素亮度值的加权平均代表某个像素的强度。相较于高斯滤波，BF模型增加了对图像边缘的保护。BF组合了空间域和值域核函数，使得输出图像与空间邻近度和像素值相似度均有关，即输出像素不仅与像素空间距离相关，还与像素点的像素差值相关。

BF中，输出像素的值f BF(x，)y依赖于邻域像素值的加权组合，定义为：

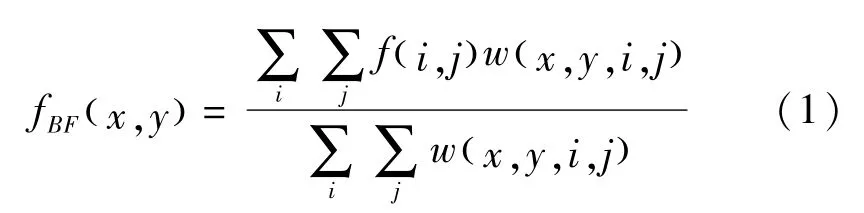
权重系数w(x，y，i，j)（即核函数）取决于空间域和值域，其中，空间域权重因子为：

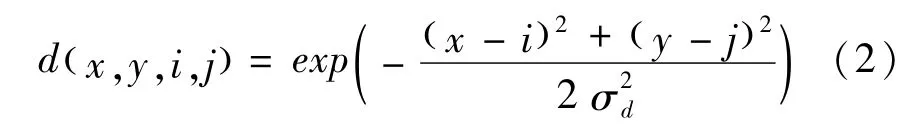
值域权重因子为：

BF的权重w(x，y，i，j)等于空间域权重因子和值域权重因子的乘积：

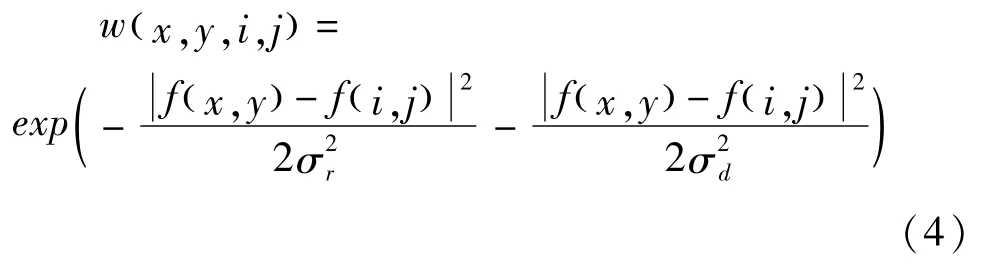
式（2）中，σd是空间域方差。σd越小，图像边缘和细节越清楚，σd越大，图像越模糊。d(x，y，i，j)等同于高斯滤波系数。

式（3）中，σr是值域方差。在图像平滑区域，σr越大，平滑噪声能力越强；而在边缘，σr越小，能保留的边界特征越多。r(x，y，i，j)与空间像素差值相关。

实际应用中，在图像非边缘区域，像素差值较小，σr变大，此时，空间域方差σd起主要作用，等同于普通的高斯滤波，保边性能下降；在图像边缘，像素差值较大，σr变小，w(x，y，i，j)减小，当前像素受到影响就越小，从而保持了边缘信息。

图1是BF模型核函数产生过程，该图是在大小为9×9（由0和1组成）的模板上构造的二值图像，图1（a）、（b）、（c）分别是 BF空间域函数（设 σd=2）、值域函数（σr=0.2）（在边缘（5，5）处）及 BF核函数图像（分别用 D、R、W 函数表示式（2）、（3）、（4）对应函数）。其中，D函数表示区域的位置关系，R函数体现像素的灰度关系。当输入有噪声和边缘的图像，通过核函数W 运算后，就可以得到降低噪声并增强边缘信息的图像。

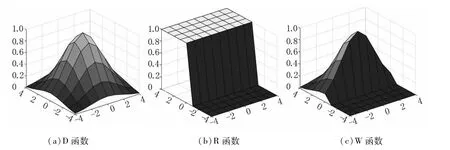
图1 BF模型核函数图像Fig 1 BF model kernel function image

图2是一幅甲状腺超声图像滤波后的图。其中，图2（a）为原图，图2（b）、图2（c）分别对图2（a）进行双边滤波、高斯滤波操作，为消除使用B超测量甲状腺径线，图2（d）在图2（b）基础上增加中值滤波操作。

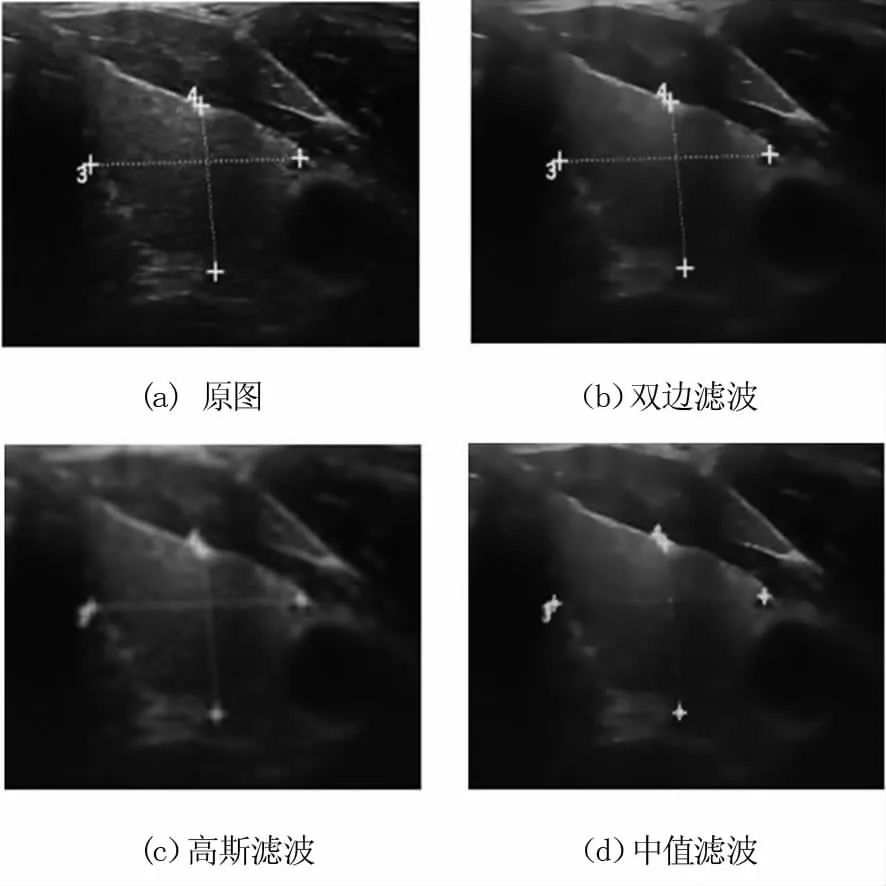
图2 甲状腺超声图像双边滤波结果Fig 2 Bilateral filtering results of thyroid ultrasound images

2.2 DRLSE模型

为解决水平集演化重新初始化问题，Li[19]提出一种增加惩罚项的方法，极大提高了曲线演化速率。但引入的惩罚项会造成扩散率趋于无穷大，导致曲线演化无法到达期望的边界。因此，Li等[16]又在能量函数中添加正则化项，使扩散率保持为一个有界常数，从而实现演化曲线无需重新初始化即能到达目标区域边界，该方法即DRLSE模型。此模型是基于能量泛函的活动轮廓模型。令Ω为图像区域，I（x，y）为Ω→R上的灰度图像，能量函数定义为：

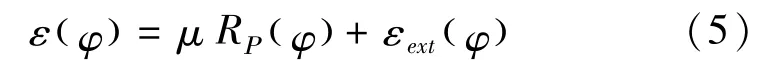
其中，φ（x，y）是定义在域Ω→R上的水平集函数，μ＞0，是正则化项权重参数，Rp(φ)是正则化项，定义为：

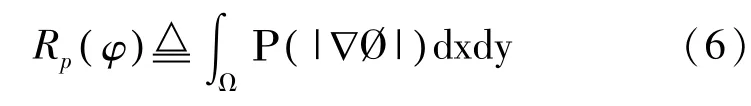
Ρ为势函数，即：

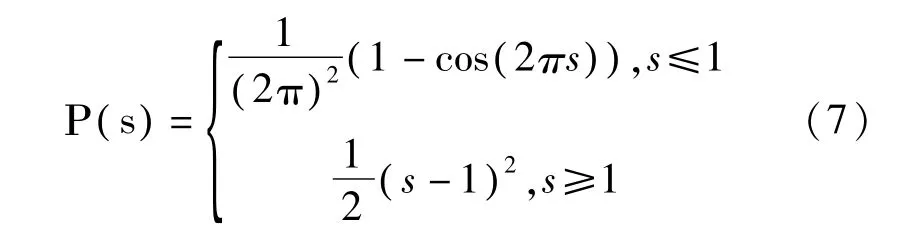
引入Ρ是为了使φ（x，y）在零水平集附近保持符号距离特性，即同时，在远离零水平集的位置，保持εext(φ)为外部能量，定义为：

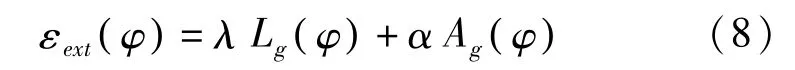
其中，λ＞0，α∈R。Lg(φ)是以g为权重的加权长度项，Ag(φ ) 是以g为权重的加权面积项。Lg(φ)和Ag(φ )分别定义为：

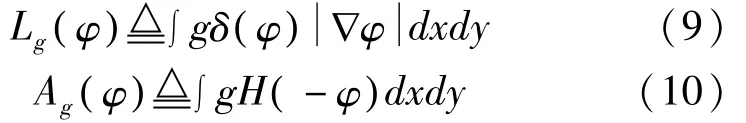
其中，g为边缘指示函数，其作用是使零水平轮廓能停止在目标区域边缘，定义为：

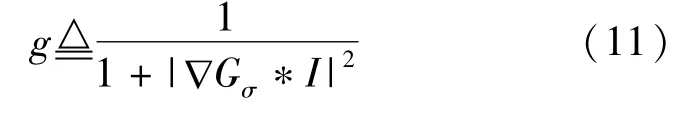
其中，Gσ为标准偏差为σ的Gaussian内核函数。

式（9）、（10）中，δ和H分别是 Dirac函数和Heaviside函数。一般可使用近似的δε和Hε，即：

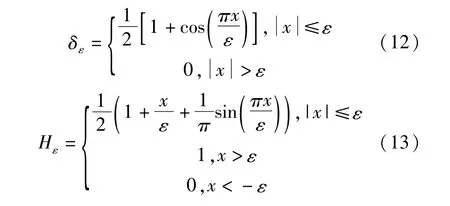
综上，能量泛函为：

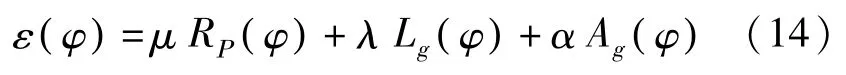
其中，λ＞0，α∈R。

能量泛函的最小化可由以下梯度流来求解：

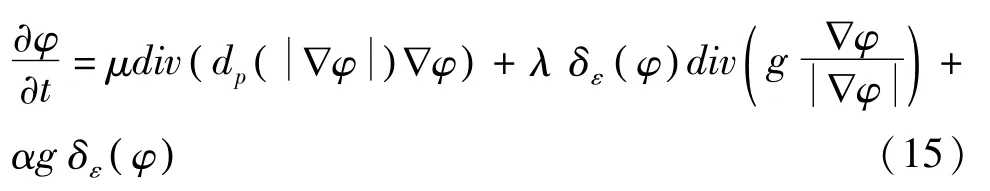
式中第一项对应正则化项。第二项对应加权长度项，用于调整φ的零水平轮廓，驱使曲线按照平均曲率的方式朝目标边界演化。当曲线某一点曲率为正，向内收缩，为负则向外扩张。第三项αgδε(φ)对应加权面积项，用于加快演化曲线运动，当α为正时，轮廓向内收缩，α为负时，轮廓向外扩张，从而驱动零水平集曲线向边界演化。

式（15）中后两项都涉及控制曲线演化位置的边缘指示函数g。由式（11）知，g是严格非负递减函数，它依赖于图像的灰度，通常选高斯平滑后的梯度信息来进行运算，因此g对噪声极其敏感。一般情况下，当演化曲线位于图像中边缘时，灰度变化较大，梯度较大，g近似为0，曲线停止演化；曲线远离边缘时，梯度值相对较小，g不为0，曲线继续演化。但是，超声图像中噪声较大，可能导致曲线演化停留在当前噪声点，而不继续演化，致使曲线无法演化到目标边界。而且，若图像存在弱边缘，曲线演化到边界附近，g的值仍充分大，曲线还有较大演化速度，致使曲线越过边界继续演化，造成边界泄露，定位不准确。故本研究提出一个新的边缘指示函数。

2.3 改进边缘指示函数

鉴于甲状腺超声图像的噪声大且边界模糊，提出综合考虑噪声和边界强弱的边缘指示函数，定义为：

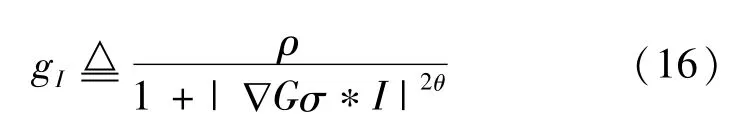
其中，ρ为控制曲线收敛速率的参数，θ为控制噪声敏感度的参数。ρ＞0，θ＞0，且均为常量。经实验分析，分割甲状腺超声图像时，ρ、θ最优取值分别为：ρ取1～100，步长是1；θ取0.1～2，步长0.1。实际应用中，ρ和θ相互作用，具体取值应根据各个图像特征实时调整。

若图像目标边界较强，则取较小ρ值；反之，取较大ρ值，以加快gI收敛到0的速率，使其在弱边界也能快速收敛。

若图像噪声较小，可取较大θ值来加速演化；若图像噪声较大，则取较小θ值，使演化曲线可以跳过噪声点继续演化，直到停止在目标边界。

3 实验结果及分析

本研究分别对六幅受噪声污染程度和边界清晰度均不同的甲状腺超声图像进行分割实验，以验证算法的有效性。实验环境为Intel（R）Core（TM）i7-6700 CPU 3.40 GHz，RAM：8 GB。操作系统：Windows 7，软件环境：MATLAB 2014a。实验图像均来源于南京同仁医院。

六幅实验图均使用三种不同边缘指示函数，并对比迭代次数和运行时间。除改进的gI外，另两种边缘指示函数分别为Li在DRLSE中使用的和刘哲等[17]改进的也依赖于图像灰度信息，对噪声非常敏感。

图3～图8是本实验选用的六幅甲状腺超声图像分割结果。

图3 噪声较大边界不连续的甲状腺超声图像的分割Fig 3 Segmentation of thyroid ultrasound images with large noise and discontinuous boundaries

图4 噪声大边界较模糊的甲状腺超声图像的分割Fig 4 Segmentation of thyroid ultrasound images with large noise and blurred boundaries

图5 噪声较小边界较弱的甲状腺超声图像的分割Fig 5 Segmentation of thyroid ultrasound image with small noise and weak boundary

图6 噪声较小边界较模糊的甲状腺超声图像的分割Fig 6 Segmentation of thyroid ultrasound images with small noise and blurred boundaries

图7 噪声小边界较清晰的甲状腺超声图像的分割Fig 7 Segmentation of thyroid ultrasound images with small noise and clear boundaries

图8 噪声小边界清晰的甲状腺超声图像的分割Fig 8 Segmentation of thyroid ultrasound images with small noise and clear boundary

对比图3～图8中的（a）、（b）图可知，对（a）图进行双边滤波得到（b）图，此过程有效降低了斑点噪声，保护了甲状腺区域的边界信息。

本研究改进gI的参数设置见表1（分别对应图3～图8中（e）图）。其中，图3（a）、图4（a）噪声污染严重、甲状腺边界较强，故实验采用较小θ值（0.8和0.7）和较小的 ρ值（20和23）。图5（a）、图6（a）甲状腺边界较弱、噪声斑点也较弱，故选取了较大ρ值（50和80）和 θ值（1.2和 1.4）。图 7（a）、图 8（a）是本实验中甲状腺边界最强的两幅图，故选用本研究最小ρ值（15和18）。

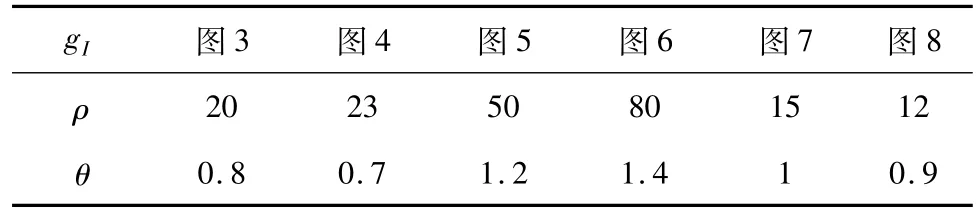
表1 改进边缘指示函数gI参数设置Table 1 Parameter setting of improved edge indicator function gI

在保证其他参数设置均不变的情况下，实验比较了使用g、g I、gL的DRLSE模型在分割甲状腺图像时所需迭代次数和运行时间（对应图3～图8中（c）、（d）、（e）），见表2。

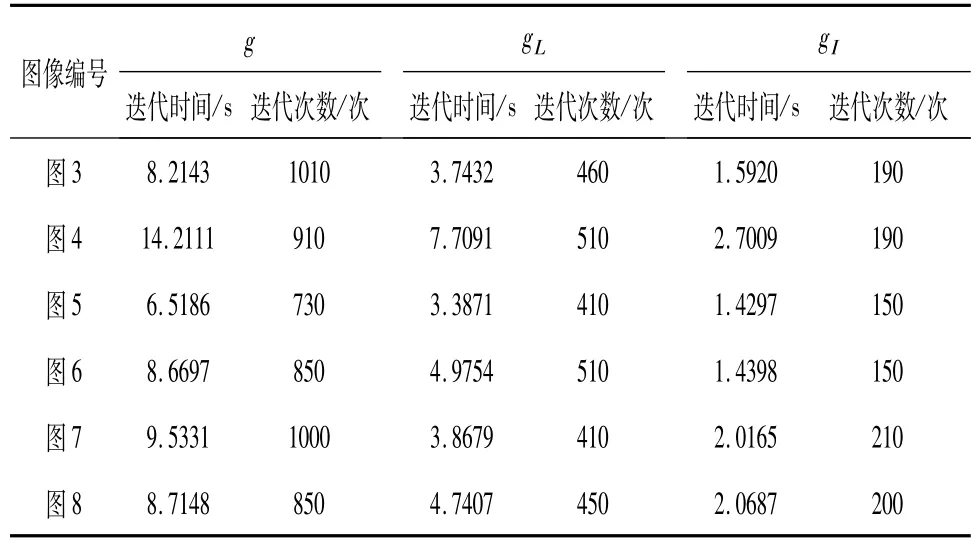
表2 分别使用g、gL和gI函数时的迭代次数和运行时间Table 2 The number of iterations and running time when using g、gL and gI functions respectively

分析表2，使用本研究改进gI的DRLSE模型分割甲状腺，明显减少了曲线演化迭代次数和运行时间，极大提高了曲线演化速率和分割效率。

本研究分割结果的准确性，采用Shattuck等[20]提出的骰子相似系数（dice similarity coefficient，DSC）来表示，其表达式为（SSEG是算法分割结果；SGT是手动分割结果；N(S)表示分割区域的面积）PDSC的数值越接近1，则表示分割精度越高，分割结果越准确。本研究中图3～图 8（c）、（d）、（e）图分割精度见表 3。

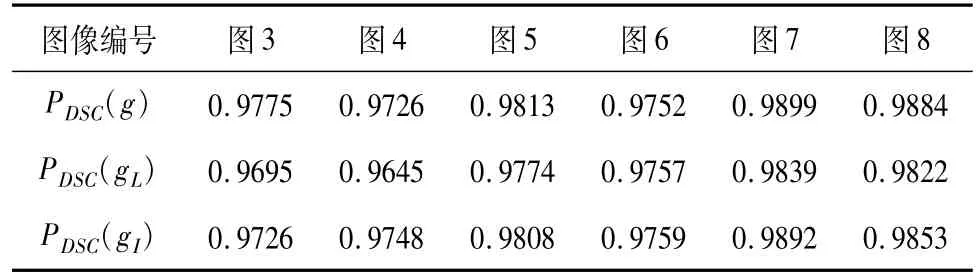
表3 分别使用g、gL和gI函数时的分割精度Table 3 Segmentation accuracy using g，gL and gI functions respectively

由表3知，DRLSE模型分别采用g、gL和gI，均能达到较高分割精度，表明均能大致分割出超声图像中的甲状腺区域。

综上，在保证图像分割精度的同时，使用本研究方法分割超声图像中的甲状腺区域，可以明显减少迭代次数和运行时间，有效地提高了曲线演化速率和分割效率。

4 结论

本研究针对甲状腺超声图像受噪声污染严重等特点，首先使用双边滤波对其进行预处理，降低了甲状腺及其周围组织区域的复杂度。然后对Li提出的DRLSE模型中的边缘指示函数进行了改进，减少了水平集演化过程中的迭代次数和运行时间，在保证分割精度的同时，有效提高了分割效率。

但是，改进边缘指示函数中参数ρ和θ的值需要人为设置，缺乏自适应性，一定程度上影响了甲状腺超声图像分割效率。因此，如何更好的、更合理的设置好参数，提高分割效率，是需要继续研究的课题。