基于自适应响应面法的脂肪组织材料参数反求*

崔世海，段海彤，李海岩，贺丽娟，吕文乐，阮世捷

（天津科技大学机械工程学院，天津300222）

1 引 言

在全球肥胖人群不断增长的趋势下[1-2]，肥胖乘员的乘车安全越来越受到关注。目前肥胖乘员的损伤机理尚不明确，有限元模型[3-5]、尸体样本[6]以及假人模型[7]等是研究乘员损伤机理、评价乘员损伤的常用工具。其中，有限元模型在肥胖乘员损伤机理研究中有着独到的优势，其可以反映身体各部分力学响应情况，且具有可重复性，同时能将混淆的影响因素单独分开。对于肥胖有限元模型，其增加的大量脂肪是影响生物力学响应的重要因素，脂肪组织材料本构的选择及参数的确定是影响其生物仿真度及损伤评价的关键因素。

皮下脂肪组织是一种位于真皮与腱膜和肌肉筋膜之间的结缔组织。脂肪组织占人体总质量的5%～60%，代表新陈代谢相关组织中最具可塑性的器官[8-9]，在吸收与分配机械载荷中起着重要的作用，可以吸收冲击和防止局部应力集中，对人体起到一定的保护作用。就软组织而言，如脑组织[10]、肝[11]与肾[12]等，其材料参数可由实验数据结合有限元仿真拟合曲线求得，但计算结果会受到样本几何形状变化的影响。Chawla等[13]采用遗传算法和有限元相结合的方法，基于冲击实验数据，获得基于Zener模型的被动肌肉组织材料特性。为消除样本几何形状变化带来的影响，Hu等[14]基于特定样本构建几何模型，根据单轴拉伸实验数据，利用遗传算法获得了胎盘组织的材料特性。Untaroiu等[15]对肌肉、脂肪与韧带等进行了拉伸与压缩实验，采用序列响应面法反求得到基于线性粘弹性材料本构的各项材料参数。这些软组织材料参数的成功获取，表明了采用有限元与优化算法相结合反求获得材料参数的可行性。目前国内外关于皮下脂肪组织材料特性的研究相对较少。Zheng等[16]从志愿者压痕实验中提取数据，拟合出准线性粘弹性材料本构的初始模量范围为0.22～58.4 kPa，非线性因子范围为21.7～547 kPa，时间常数范围为0.05～8.93 s，材料常数范围为0.029～0.277。Geerligs等[17]测量出脂肪组织剪切模量为7.5 kPa。Comley等[18]基于猪的皮下脂肪组织进行了全应变率范围的力学实验，拟合出Ogden超弹性材料本构中的Ogden系数为23，低、中和高应变率下的剪切模量分别为0.4、1.7和1120 kPa。Sims等[19]通过核磁共振成像（MRI）结合逆向有限元法获得了脂肪组织Neo Hookean材料本构的初始剪切模量为（0.53±0.31）kPa，单项 Prony级数的常数 α=0.39±0.03，τ=（700±255）s。

现有脂肪组织的材料参数一般直接引用于经典文献，或由力学实验拟合得到，一定程度上受实验测量误差及不确定因素的影响，在仿真中应用这些材料参数，往往难以体现脂肪组织的真实力学响应情况。本研究基于Ogden超弹性材料本构，对其各项材料参数进行筛选试验，选择对力学响应影响显著的材料参数作为反求目标，参考Comely等[18]的中应变率脂肪组织压缩实验，构建脂肪组织有限元模型，通过有限元方法与优化策略相结合实现脂肪组织材料参数的反求，并分析应用反求参数获得的仿真曲线与实验曲线的相关性。

2 材料与方法

2.1 有限元模型构建

交通事故中人体受到的冲击一般在中应变率范围内，参照 Comley等[18]的中应变率（20 s-1）压缩实验进行仿真试验。运用CATIA重构脂肪组织与压板的几何模型，其中脂肪样本直径为10 mm，厚度为3 mm，导入Hypermesh中划分网格，脂肪组织与压板均采用8节点6面体单元模拟，脂肪组织有限元模型共有1 348个单元，1 350个节点，见图1。

图1 中应变率脂肪组织有限元模型Fig 1 Finite element model of medium strain rate adipose tissue

2.2 仿真设置

仿真试验参照压缩实验设置，下压板固定，上压板沿脂肪组织轴向（Z方向）加载。为方便接触计算，在脂肪组织上覆盖一层壳单元并赋予空材料，不会影响刚度计算，与上、下压板设置为面-面接触。脂肪组织与上、下压板间静摩擦系数为0.1，动摩擦系数为0.05，仿真中上、下压板材料参数设为刚体。目前国内外常用于模拟脂肪组织的材料本构模型有线性粘弹性材料本构，Mooney-Rivlin超弹性材料本构和Ogden超弹性材料本构，其中Ogden超弹性材料本构模型是接近不可压缩的超弹性模型，Comley等[18]与 Calvo-Gallego等[20]指出，一阶 Ogden超弹性材料本构能够良好的表现脂肪组织力学性能，因此，本研究采用LS-DYNA材料库中Ogden超弹性材料本构模拟脂肪组织，其应变能密度函数为：

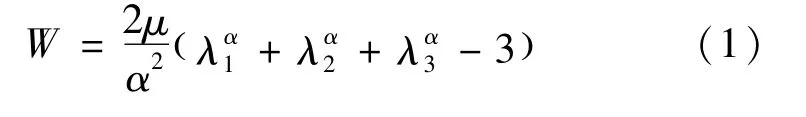
式中，μ为剪切模量，α为Ogden系数。

该模型中粘弹性响应表达形式为：

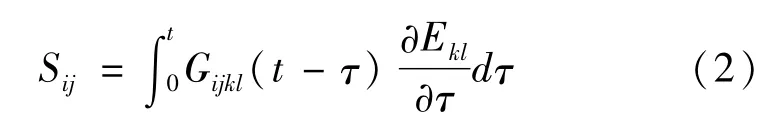
式中，Gijkl为松弛函数。考虑脂肪组织的应变率依赖性，引入由Prony级数中的六个项表示松弛函数，其方程为：

式中，Gi为剪切松弛模量，βi为衰减常数。

2.3 材料参数筛选试验设计

考虑到材料本构中各项参数对目标响应的影响程度不同，对Ogden超弹性材料本构的各项参数进行筛选试验设计，确定各项参数对力学响应的影响程度，忽略对力学响应影响很小的材料参数，仅对力学响应影响较大的材料参数进行反求，以保证在反求结果具有较高精确度下提高计算效率，降低计算成本。

Ogden超弹性材料本构的材料参数包括剪切模量μ、剪切松弛模量Gi、Ogden系数α和衰减常数β 4个因子，各个因子水平设计见表1。

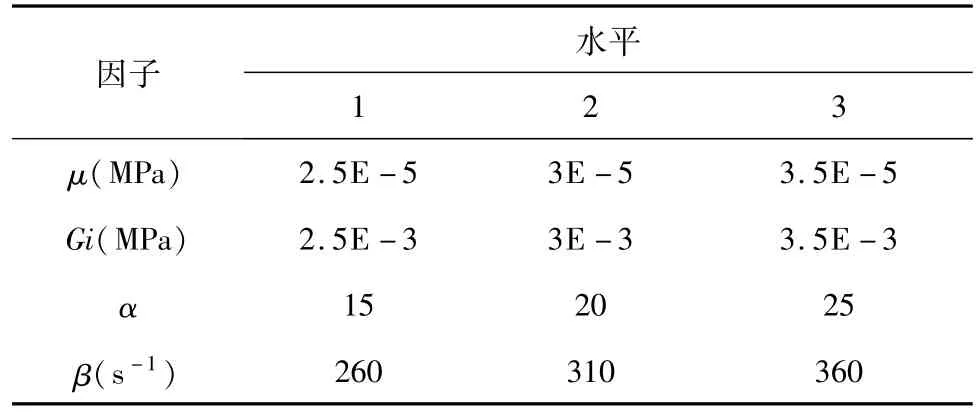
表1 各个因子水平设计Table 1 Design of each factor level

应用Hyperstudy对Ogden超弹性材料本构的各个因子进行筛选试验，Comley等[18]的压缩实验给出了应力-应变实验数据，而仿真中无法直接输出应力-应变数据，但其可由接触力-时间换算得到，接触力-时间曲线呈“J”型具有非线性单一增长趋势，因此，以接触力最大值为目标响应，能够有效地反映各材料参数对力学响应的影响程度。从全因子试验设计中得到各个因子主效应图与回归系数图，见图2。图2（a）为剪切模量μ、剪切松弛模量Gi、Ogden系数α和衰减常数β4个因子对目标响应的主效应图。图2（b）中为各个因子的回归系数，回归系数越大，表示该因子对目标响应的影响越大。

Ogden超弹性材料本构的试验结果表明，剪切松弛模量Gi和Ogden系数α均与目标响应呈正相关，其中，Ogden系数α对最大接触力值影响最显著，而剪切松弛模量Gi对目标响应的影响基本可忽略。剪切模量μ和衰减常数β均与最大接触力呈负相关，对最终目标响应的影响基本可忽略。

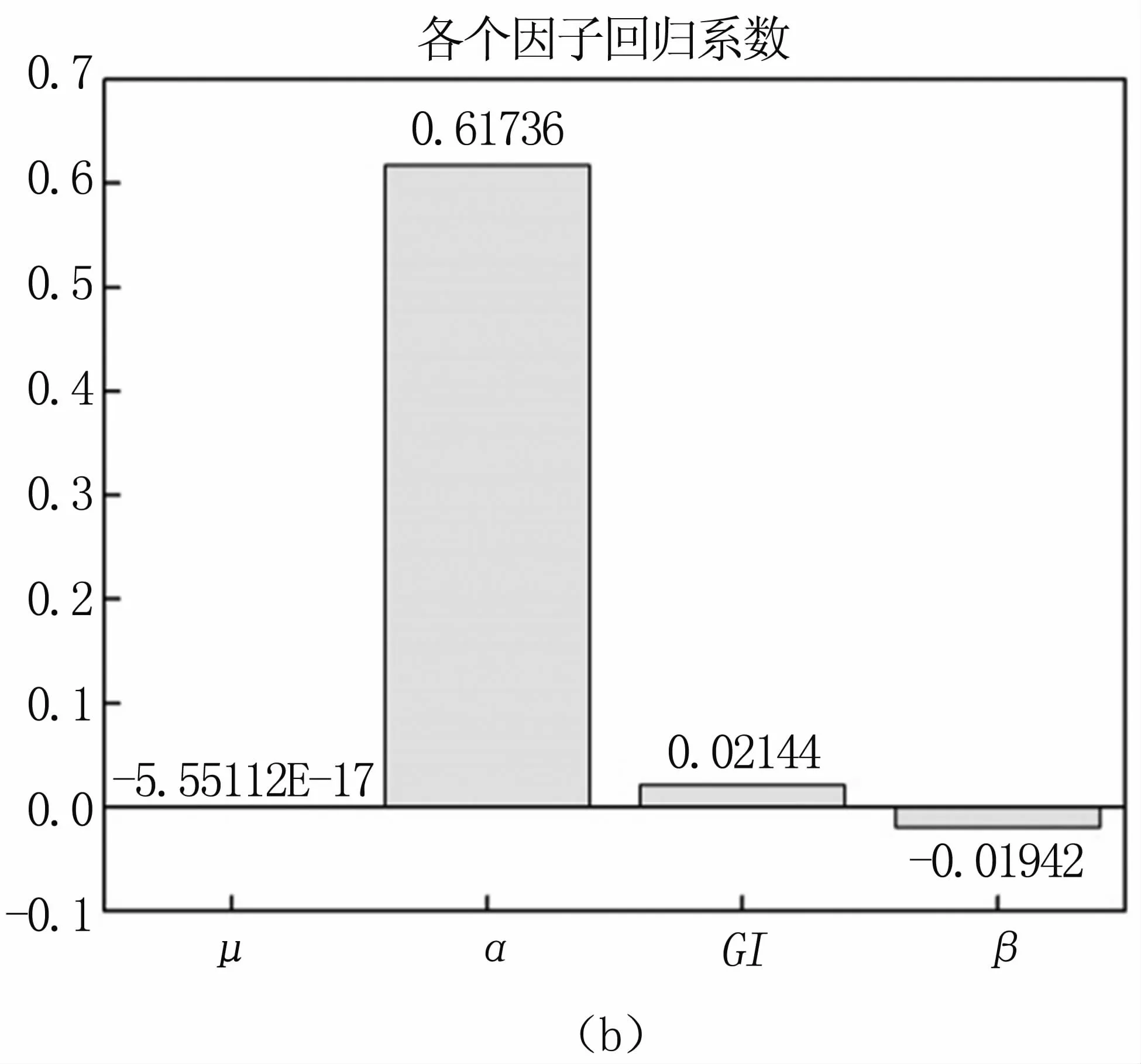
图2 筛选试验设计结果Fig 2 The results of selected experiment design

3 参数反求方法

本研究参数反求通过有限元仿真与优化算法相结合，采用自适应响应面法（ARSM）不断调整设计变量的取值，使目标函数达到最小并输出最终各设计变量的取值，实现材料参数的反求。在ARSM中由二阶多项式拟合得到的目标函数及约束函数为：

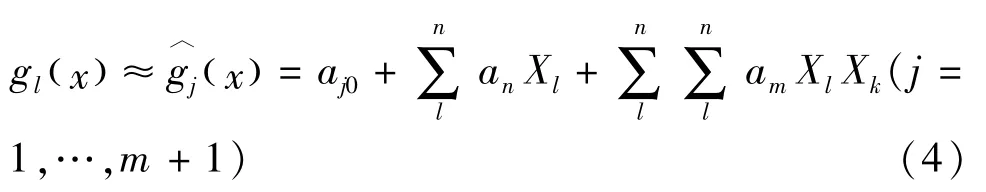
式中，m为约束的个数，n为设计变量的个数，aj0、an、am为二次多项式系数。

ARSM以序列二次规划为核心优化引擎，通过高效算法拟合响应面接近感兴趣设计点，引入移动限制以保证算法的鲁棒性。该优化算法分析初始设计点及由扰动设计变量生成的n个新的设计点，使用最小二乘法确定目标函数的多项式系数，用数学规划法对基于响应面的问题进行优化求解，自动选取最优化方法对模型近似最优点进行分析，若不收敛则继续寻优，直至迭代收敛时停止求解[21]。反求流程见图3。

图3 材料参数反求流程Fig 3 Process of material parameter inversion

根据筛选试验设计结果，选择对力学响应影响最显著的Ogden系数与相对较大的剪切松弛模量作为反求目标材料参数，其材料参数取值范围见表2[18，22-24]。

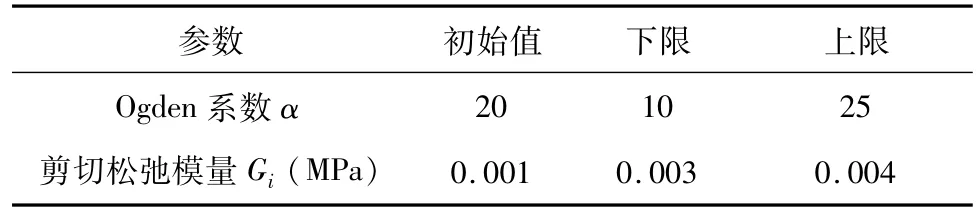
表2 材料参数取值范围Table 2 Range of material parameters

将仿真曲线与实验曲线之间所夹面积的最小值定为优化目标，使仿真曲线与实验曲线尽可能的吻合，将最小化问题转换成一个普通优化问题，其目标函数为：

其中v1x、v1y分别为仿真曲线X轴、Y轴数据，v2x、v2y分别为实验曲线X轴、Y轴数据。

4 反求结果与讨论

反求计算迭代13次达到收敛，见图4。由于Ogden超弹性材料本构能够良好的体现脂肪组织的力学性能，且各项材料参数的初始值选择得当，取值范围变化较小，因此，仿真中初始目标函数与实验结果相差较小，最终收敛值约是目标函数初始值1/3，但使仿真结果极大地逼近了实验结果，表明了反求得到的材料参数具有更高的生物仿真度。

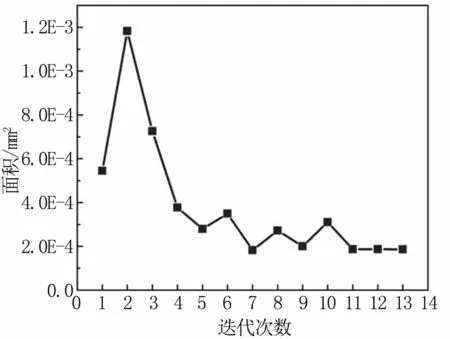
图4 目标函数优化历程Fig 4 The optimization process of the objective function

反求得到Ogden系数α为19.982，剪切松弛模量Gi为 1.703 KPa，Comley等[18]拟合得到的 Ogden系数为23，剪切松弛模量为1.7 KPa。反求与拟合得到的剪切松弛模量大致相同，由于Ogden系数对目标响应影响最显著，虽然反求比拟合得到的Ogden系数约低13%，但能够极大地提高脂肪组织的生物仿真度。初始仿真曲线、反求仿真曲线与实验结果的对比见图5。采用Origin分析反求仿真曲线与实验曲线的相关系数为0.98876，与实验结果吻合良好，证明了采用该反求方法获得的脂肪组织材料参数具有更高的生物仿真度。

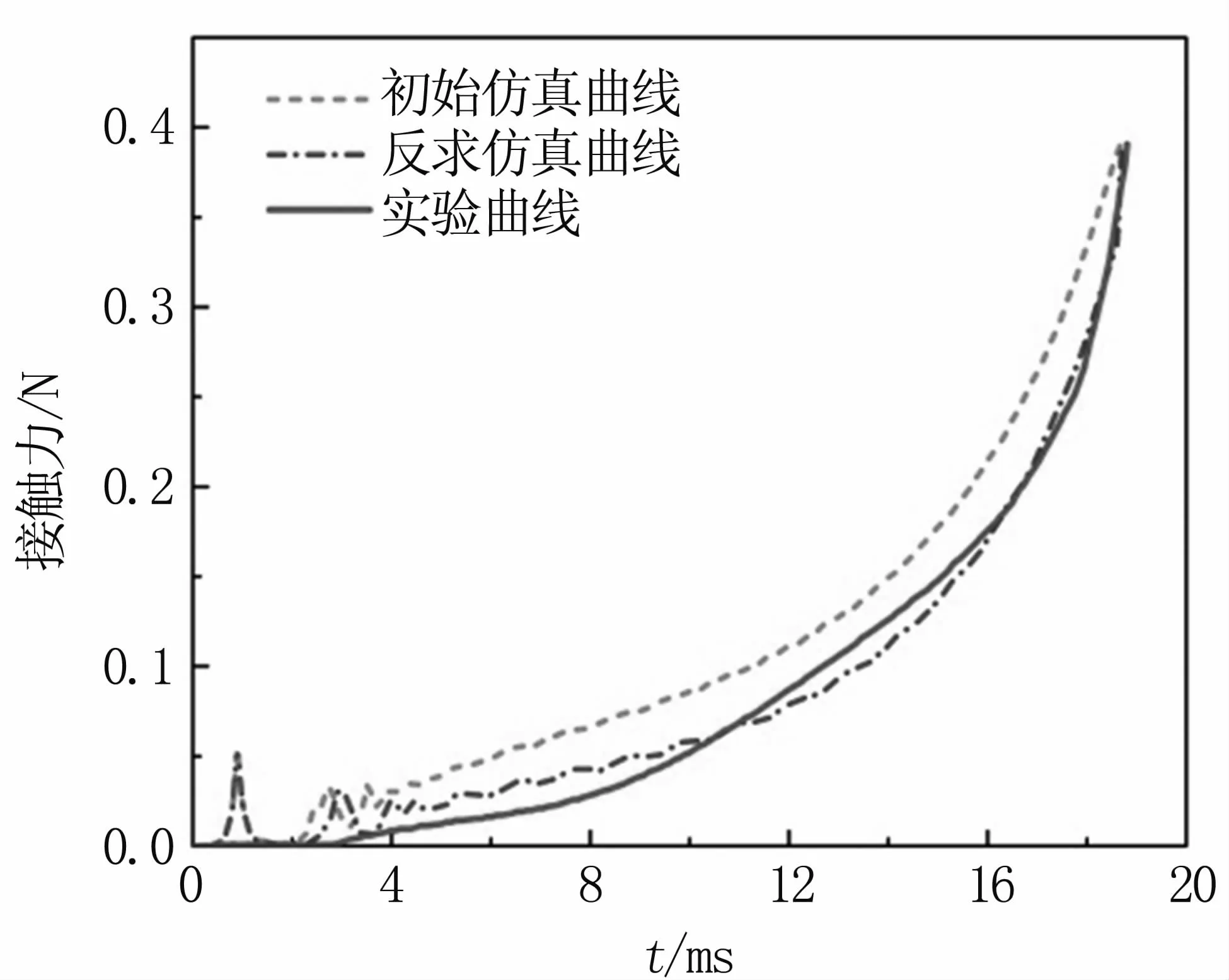
图5 反求与实验结果对比Fig 5 Comparison of result between reverse and experimental

5 结论

本研究参照Comley等[18]的压缩实验数据，采用有限元仿真与优化策略相结合的方法，对Ogden超弹性材料本构中两项对力学响应影响较为显著的材料参数进行反求，得到Ogden系数为19.982，剪切松弛模量为1.703 KPa。应用反求得到的材料参数进行仿真输出的仿真曲线与实验曲线的相关系数为0.98876，与实验结果吻合良好，表明在仿真中采用该反求方法获得的脂肪组织材料参数具有更高的生物仿真度。

本研究所应用的脂肪组织材料参数反求方法能够有效地提高计算效率，降低计算成本，仿真中利用该方法反求获得的脂肪组织材料参数具有更高的生物仿真度，同时这种反求方法也为其他材料参数的获取提供了新思路，具有较高的应用与参考价值。