基于奇异值分解方法的磁感应磁声断层重建算法*
马任,杨铭,张顺起,周晓青,殷涛,刘志朋
(北京协和医学院中国医学科学院生物医学工程研究所,天津300192)
1 引 言
医学相关研究表明,癌症的早期诊断可以提高治愈率[1]。通过医学成像方式,例如X射线断层成像、核磁共振成像(MRI)及正电子发射断层成像(PET),可以进行癌症的诊断,目前X射线断层成像及核磁共振成像的早期诊断精确度不高,PET虽然可以进行癌症的早期诊断,但其具有放射性,且检查价格昂贵,并不适用于癌症早期筛查及诊断。当人体组织发生癌变时,癌变部位的电特性会与其他部位不同,癌变组织和正常组织之间电特性参量也会存在明显差异,科研人员通过离体组织电特性测量实验证明在癌变的早期,癌变组织的电导率约为正常组织的6.4倍,而介电常数约为正常组织的3.8倍,最高可相差高达一个数量级[2]。电特性的差异可以作为成像对比度,从而实现对癌症的早期诊断。目前,可以实现检测这种电特性差异的方法有采用电磁场直接检测方法,包括电阻抗成像[3]及磁感应成像[4]。同时,为了提高成像分辨率,研究人员提出采用电磁场及声场互相耦合的新型电阻抗成像方式,这些方法主要有霍尔效应成像[5-6],磁声成像[7-8]以及磁感应磁声成像[9-10]等。
磁感应磁声成像(magnetoacoustic tomography with magnetic induction,MAT-MI)是将阻抗成像与超声检测相结合,利用超声检测分辨率高的优点,将组织内部电导率通过磁声耦合效应转化为超声信号传出体外并重建组织电导率分布。近年来,由于激励源特性、信号处理方法与重建算法及理论的改进,偶极子源[11],矢量源重建算法[12]及基于真实声换能器特性的重建算法[13-14]相继被应用于磁声成像中,磁声成像的实验仿体也逐渐从高电导率的铜环、石墨等金属扩展到低电导率的类生物组织明胶琼脂仿体,随后离体猪肉,肝脏也可进行粗略成像,电导率图像质量已经能分辨出脂肪和肌肉的边界轮廓,但是目前实验结果尚不能利用检测声信号重建非边界位置的内部电导率信息。为了研究MAT-MI中电导率分布与检测超声信号之间的关联,实现电导率定量重建,本研究基于MAT-MI原理,建立了一个系统矩阵,通过截断奇异值方法(TSVD)对MATMI算法进行仿真研究。
2 理论分析
MAT-MI是从待成像组织的电阻抗分布到检测到的超声信号的转换过程。其基本原理是将待检测组织置于稳恒磁场B中,同时外加相同方向的脉冲变化磁场B1,脉冲磁场在组织内部产生感应电流J,与静磁场B相互作用会产生洛仑兹力,从而激发组织产生同频振动,该振动会向组织外传播包含成像物体电特性的超声信号,通过重建算法即可重建出组织的电导率分布图像。在MAT-MI中,声源振动是由时变洛伦兹力产生,而洛伦兹力与感应电流、静态磁场相关,感应电流又与时变磁场、成像物体的电导率相关,因而,通过声源重建,并建立与成像物体电导率之间的关系,可以得到电阻抗断层图像。MAT-MI声源的对比度和空间分辨率决定了电阻抗图像的质量。
根据上述成像原理,可知MAT-MI是通过采集边界超声信号重建组织内部的电导率分布,其系统模型见图1,包含从电导率分布到产生超声信号过程中的各种物理耦合效应,超声换能器特性及磁感应磁声实验系统的设置等参数。对于固定的实验系统,该系统模型方法可以有效的抑制噪声,提高成像分辨率。因此,MAT-MI的研究就转化为对系统模型特征分析及其逆系统求解的研究。
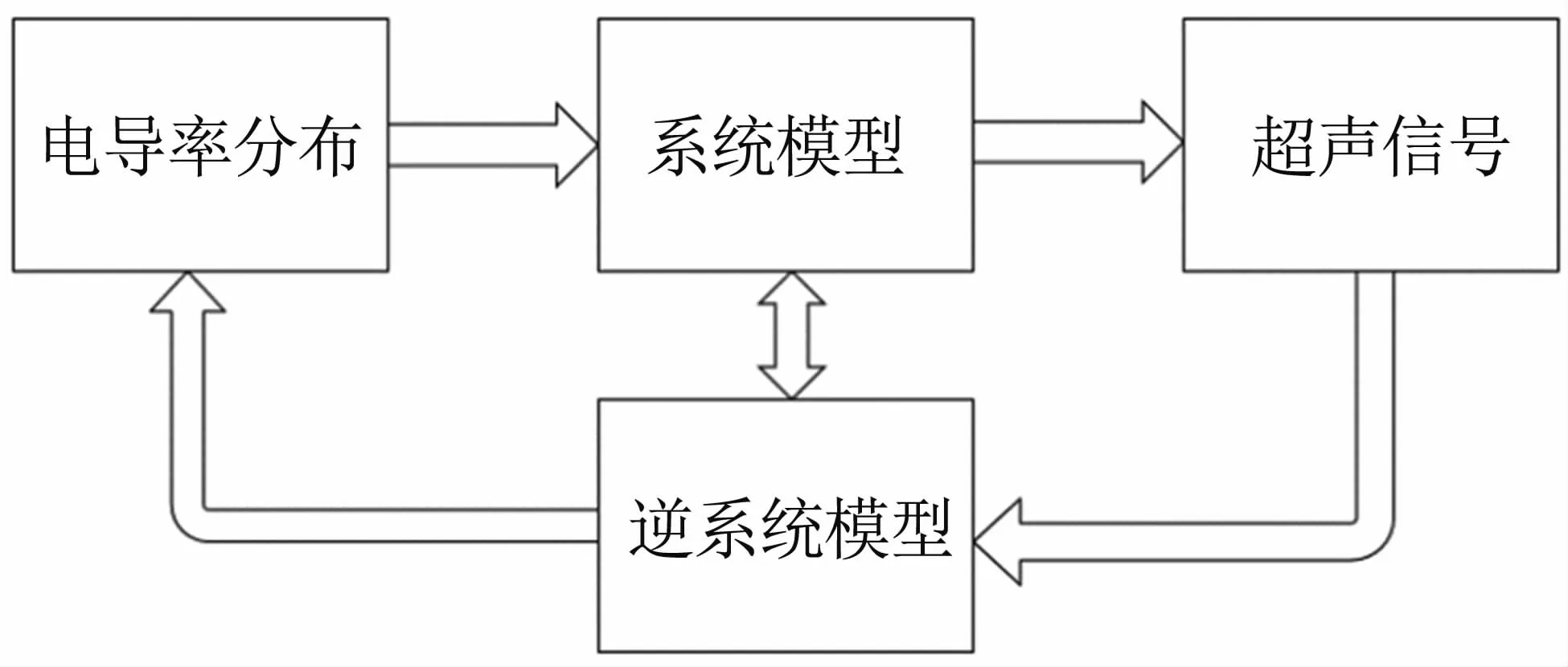
图1 磁感应磁声成像的系统模型Fig 1 The system model of MAT-MI
3 方法
3.1 系统矩阵及其伪逆矩阵
在MAT-MI中,磁场、感应涡电流及声压是时间和空间的函数,根据生物组织中电场磁场声场的机电耦合机制[15],声压分布由以下波动方程表示:
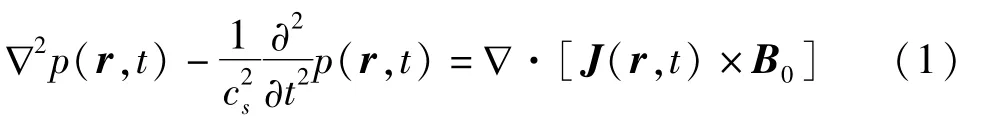
其中cs是声在组织中传播的速度,p(r,t)是声压场的时空分布,J(r,t)是感应涡流密度,r为无界空间中的任一点,∇·[J(r,t)×B0]是声振源。根据矢量分解公式,该声振源可以表示为:
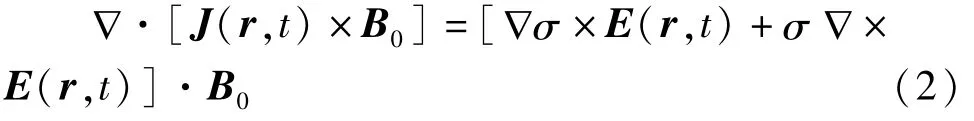
由声场在自由空间中的格林函数公式,求解声压波动方程可得:
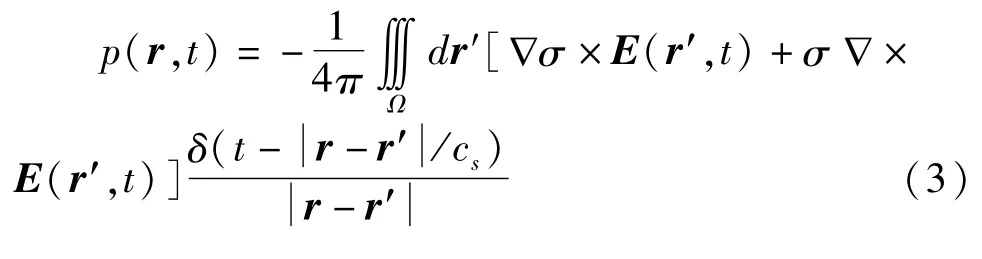
对于电导率均匀变化的组织,上述公式说明电导率与电导率的梯度经过一个系统矩阵可以得到相应的超声信号,式(3)可以抽象为一个积分方程的形式,如下:
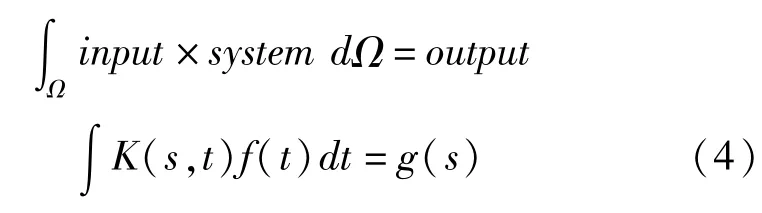
对于n×n的电导率成像区域,检测换能器个数为m,每个换能器的采样点数为k。磁感应磁声成像的系统矩阵模型建立方法见图2,抽象为矩阵形式见式(5),其中A为磁感应磁声成像系统矩阵,其矩阵大小为mk×n2,x反映了待成像区域的电导率分布,b为检测超声信号。

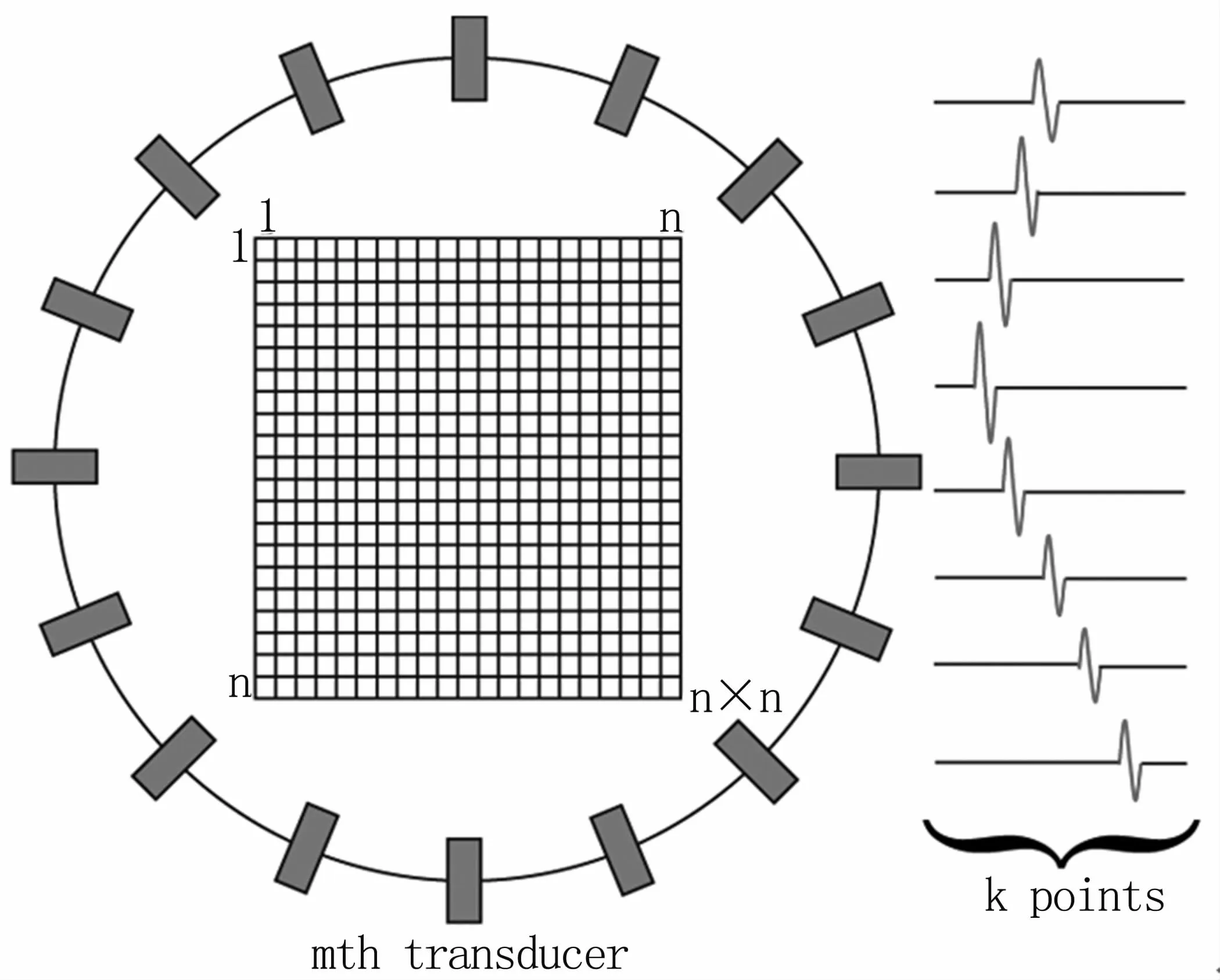
图2 磁感应磁声成像系统矩阵模型的建立Fig 2 The system matrix of MAT-MI
对于该不适定矩阵方程有很多正则化方法求解,本研究采用截断奇异值分解方法(TSVD)[16]进行求解,即将矩阵A分解成特征值与相应的特征向量,具体如下:

其中,U和V为正交矩阵,∑为对角矩阵,其对角线值为系统矩阵的特征值。这些特征值反映了电导率分布与超声声压的线性关系,采用TSVD方法求A的逆矩阵为:

其重建电导率分布可由式(8)给出:

3.2 数值仿真方法
为验证上述算法的有效性,建立一个原始电导率分布模型,模型内部采用不同形状及不同电导率进行区分,外部椭圆结构的电导率设定为0.1 S/m,内部包括一个电导率为0.25 S/m的小椭圆结构,还有电导率为0.35 S/m的一个正方形结构和一个三角形结构,该原始电导率分布见图3。采用的静态磁场强度B0为1 T,为保证脉冲激励的均匀性,激励磁场采用赫姆霍兹线圈产生,该线圈注入电流密度设定为107A。

图3 原始电导率分布仿体模型Fig 3 The phantom of original conductivity distribution
设定求解域为一个50 mm×50 mm的求解空间,将该求解空间分为201×201的正方体网格,使用MATLAB进行有限差分计算,设定采集换能器的个数为60个,采样501个点,中心频率为1 MHz,扫描半径为45 mm,利用上述条件设置可以求解系统矩阵A,可知该系统矩阵A为一欠定矩阵。利用该系统矩阵经过正问题计算可得到检测声压正弦图,通过这些检测到的声压,对A进行SVD分解,按照其噪声级别,便可重建仿体模型的电导率的分布,该数值仿真方法流程图见图4。
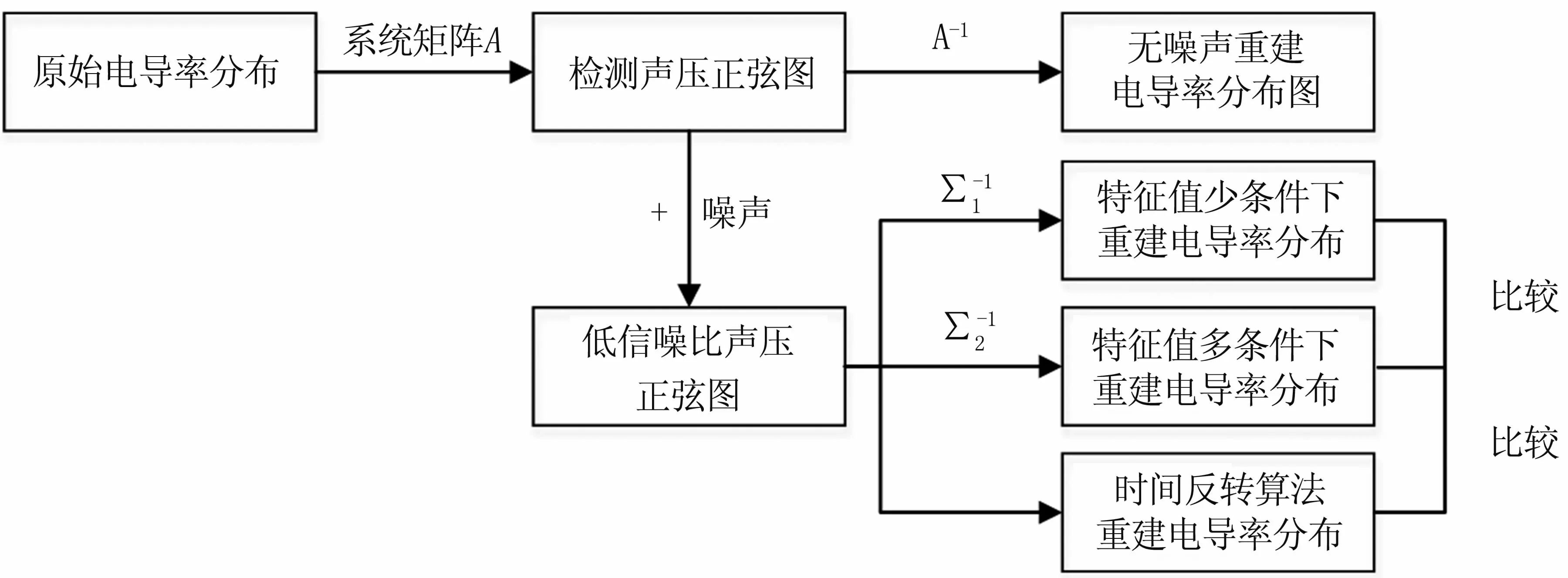
图4 基于系统矩阵重建方法数值仿真示意图Fig 4 Image of simulation based on system matrix method
4 结果
根据上述仿真过程,采用无噪声及信噪比为40 dB的含噪声磁声信号分别重建,图5给出了磁感应磁声系统矩阵A的特征值曲线,可以看出,特征值是不断下降的,且下降的速率很快,最大特征值大约为1.5,最小特征值大约为10-16,因此,在当前实验系统下,我们只能选取部分特征值进行重建,并根据噪声水平可选择截断的位置,随后采用式(8)进行电导率分布重建。
重建结果见图6,当信噪比为40 dB时,图6(a)给出了使用特征值为1 500时的电导率分布重建结果,图6(b)给出了使用特征值为3 500时的电导率分布重建结果,图6(c)给出了使用特征值为7 500的电导率分布重建结果,为无噪声条件下的重建结果,可以得出,使用系统矩阵的特征值越多,重建结果越接近真实电导率分布,由于受到噪声的影响,使用大于7 500个特征值的重建会被噪声完全覆盖。因此,在40 dB的噪声水平下,重建中只能利用7 500个特征值进行电导率重建。为了进一步给出噪声水平与磁感应磁声重建中使用特征值数目之间的关系,算法也对无噪声理想条件下的重建进行了重建算法验证,图6(d)给出了无噪声条件下使用特征值为12 000的电导率重建结果,可以看出在欠定条件下,电导率重建结果中尚存在一些纹波噪声,但电导率重建结果与真实电导率分布基本吻合。
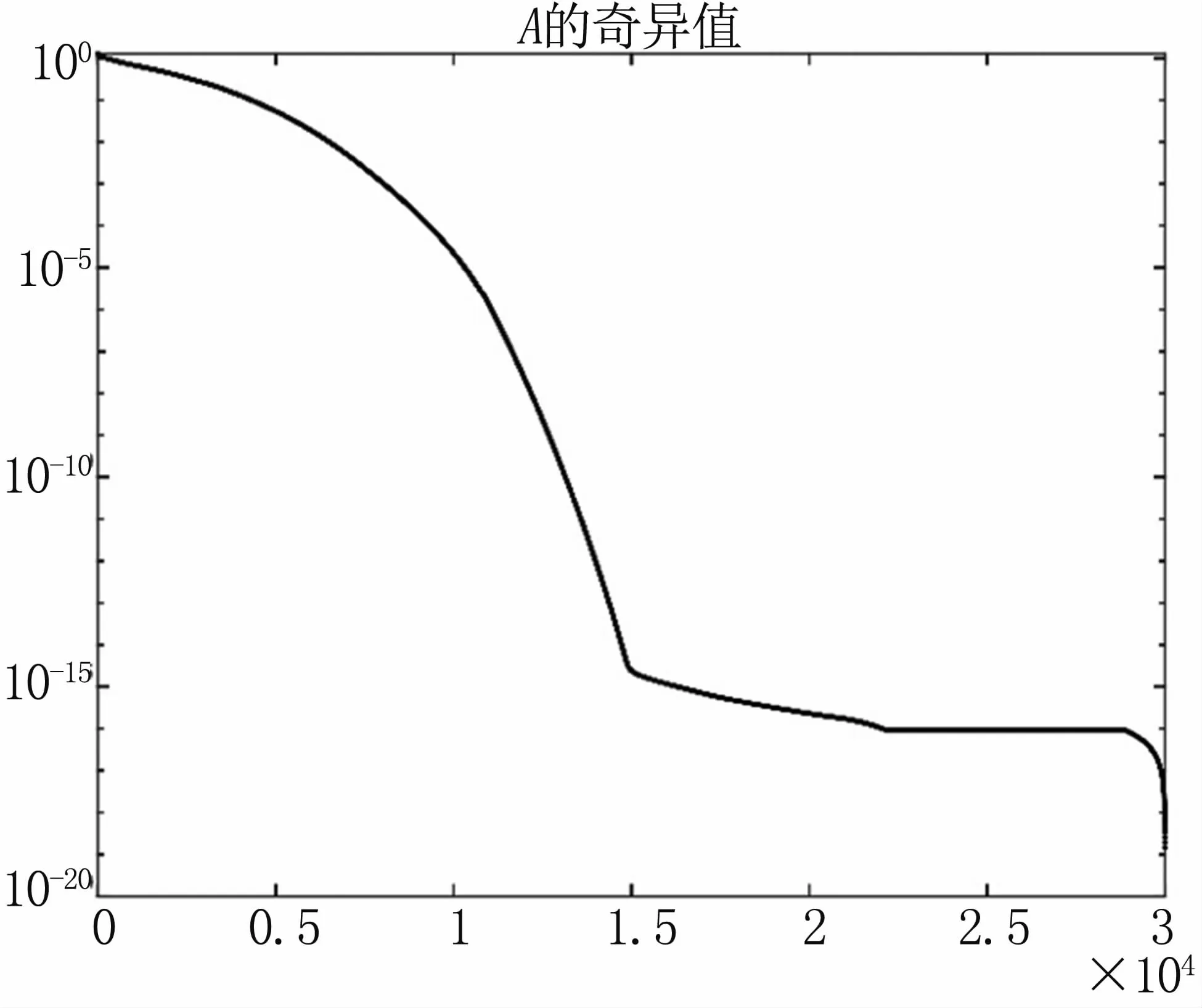
图5 系统矩阵特征值曲线Fig 5 Eigenvalues curve of system matrix

图6 不同条件下重建电导率分布结果Fig 6 Distribution of reconstructive conductivity results with different conditions
由上述结果可以得出,使用系统矩阵方法可以根据实验条件最大限度的利用磁声信号所提供的信息,使重建电导率分布结果最大限度的接近原始电导率分布。为了体现该算法的优势,我们使用相同仿真实验条件,采用磁感应磁声的常用重建算法时间反转方法进行重建,。图7给出了信噪比为40 dB时,采用时间反转方法进行电导率重建的结果。结果表明,使用时间反转算法重建的电导率分布仅有边界,仅相当于使用特征值约为1 500左右的系统矩阵算法的重建结果,其并未充分的利用磁声信号的所包含的信息。因此,通过对比可知,本研究算法的重建结果要优于时间反转方法重建结果。
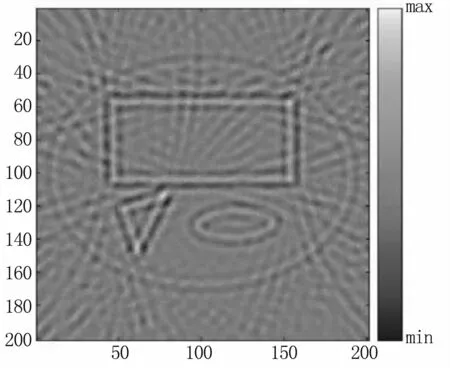
图7 时间反转算法电导率重建结果(SNR =40 d B)Fig 7 Reconstructive conductivity results by using time reversal algorithm(SNR =40 dB)
5 总结
本研究采用系统矩阵方法,对磁感应磁声电导率重建进行了仿真研究,仿真结果证明该方法可以在欠定条件及信噪比大约为40 dB的情况下重建出电导率的分布,在更低信噪比条件下,该算法也可实现电导率边界分布的重建,证明了该算法在MATMI中的适用性。相较其他方法,系统矩阵方法将从电导率分布,到磁感应磁声声源产生,传播和接收等过程精确的集成于一个系统矩阵中,通过分析该矩阵的特征值,给出了MAT-MI电导率分布与磁声信号之间的对应关系,从而最大限度的利用磁声信号中包含的信息进行电导率重建,提高了成像分辨率和精度,为磁声成像检测系统建立和应用提供基础。

