基于等效源法的近场声全息的噪声源识别与定位研究∗

陶文俊 郑明辉

（江苏科技大学 镇江 212003）

1 引言

20 世纪 80 年代，Williams 和 Maynard 等提出了近 场 声 全 息［1～2］（Nearfield Acoustic Holography，NAH）技术在运用基于等效源的近场声全息方法中，求解声源强度是不可避免的。在实际求解声源强度中，由于测量数据不可避免地会引入噪声误差，影响声源强度求解过程的稳定性，使得噪声源的识别与定位精度降低。为了抑制测量噪声的干扰，可以通过正则化方法求解声源强度，提高噪声源的识别与定位精度。但Koopmann 等［3］指出:等效源法NAH 技术要想得到满意的重建精度，传递矩阵还需要满足对角占优和尽量对称两个条件［4］。对于等效源位于声源面的近场声全息来说，由于传递矩阵对于对角占优和尽量对称两个条件的满足度较低，导致用正则化方法求解获得的声源强度并不能很好地匹配真实声场，使得基于等效源的近场声全息方法的噪声源识别与定位精度较低。通过对压缩感知算法的深入研究，发现压缩感知算法可以很好地解决该问题。

压缩感知［5～10］（Compressed Sensing，CS）理论首先是由 Candes 等在 2004 年提出，文献 2006 年才发表，CS 作为一个新的采样理论，通过开发信号的稀疏特性，突破了Nyquist采样定理的限制，其基本思想是，通过直接采集到少数线性观测数据，这些数据包括了信号的全部信息，这样就将信号的采样转化为信息地采样，最后求解一个优化问题，从压缩观测的数据中高概率的恢复原始信号。Simard［11］等将CS 用于噪声源定位识别，并且获得了较好的定位效果。东南大学赵小燕等［12］利用CS算法实现了在高混响、低信噪比环境中对噪声源的准确定位。

本文首先从理论上阐述了基于等效源法的近场声全息的信号模型，建立了声源强度求解公式，然后推导出了基于Tikhonov 正则化和CS 方法的声源强度求解方法，最后从单声源位于全息孔径内外两个角度进行分析，并从数值仿真角度分析了两种方法的噪声源识别与定位精度，结果表明，基于压缩感知和等效源的近场声全息方法具有良好的噪声源识别与定位效果。

2 信号模型

在由N 个频率相同的简单源（单极子声源）qrE（ii=1,…,N ）产生的声场中，其中，rEi为第i 个简单源的坐标，qrEi为第i 个简单源的声源强度，并用M 个离散的传声器阵列测量声场中rHj（ j=1,…,M）处的复声压 p(rHj)。假设所有的简单源分布在声源面上，则第 j 个传声器位置测量得到的复声压为

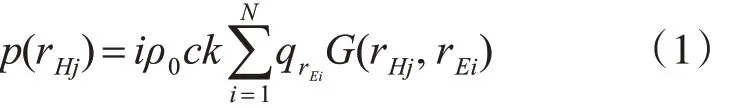
式中，ρ0为介质密度（本文为水），c 为介质中的声速，k 为波数，G(rHj,rEi) 为自由声场中的格林函数，且

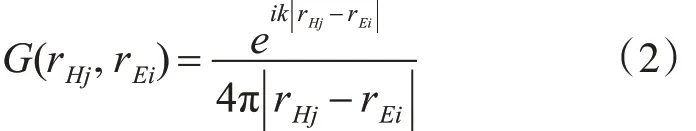
式中， ||rHj-rEi表示全息面上第 j 个传声器位置rHj与声源面上第i 个简单源位置rEi之间的距离。

定义声源面上包含所有简单源的声源强度向量为Q ，将式（1）写成矩阵形式为［8］

式中，p=[p (r),p(r),…,p(r)]T为全息面上HH1H2HM测得的声压列向量；H 为M×N 阶矩阵，是全息面上的声压和简单源声源强度之间的传递矩阵，为

式中，G为自由声场中的格林函数组成的矩阵，为

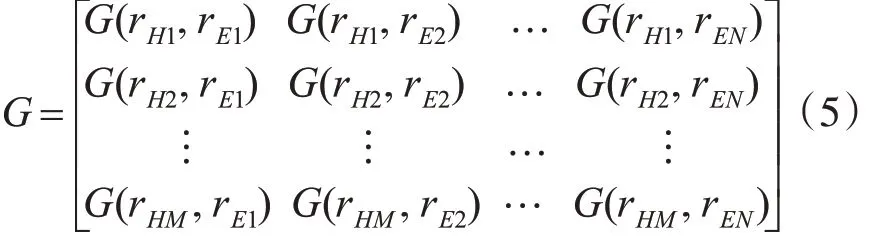
在实际应用中，测量得到的声压数据会受到噪声的影响。设有噪声模型为

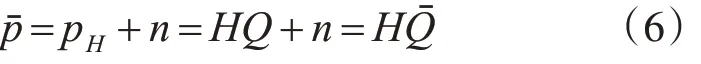
式中 pˉ为受到干扰的声压，n 为噪声向量，Qˉ为受到干扰的声源强度。

3 Tikhonov正则化声源强度估计

求解式（6）中的Qˉ属于数学物理中的反问题，然而反问题和不适定问题的联系主要表现在绝大多数反问题都是不适定的。这种不适定性主要表现在两个方面。一方面，由于客观条件的限制，反问题中的输入数据（即给定解的部分已知信息）往往是欠定的或者是过定的，这就会导致解的不唯一性或者解的不存在性。另一方面，反问题的解对输入数据往往不具有连续依赖性。由于输入数据中不可避免包含测量误差，人们就必须提出由扰动数据求反问题在一定意义下近似解的稳定的正则化方法。Tikhonov 正则化方法正是一种有效的直接正则化方法，式（6）的标准Tikhonov正则化解［13］为

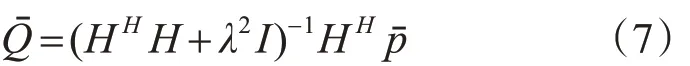
式中上标“ H ”表示共轭转置，λ 为正则化参数（本文采用L 曲线法），I 为单位矩阵，并通过正则化工具箱［14］求解。

4 压缩感知声源强度估计

4.1 压缩感知理论

假设有一个足够稀疏的信号x ∊RN，通常用l0范数表示信号的稀疏度，也就是信号中非零元素的个数满足

假设有一个观测值 y ∊RM，则观测值 y 和稀疏信号x 的关系为

式中，Φ 为一个M×N 的矩阵，通常称为压缩感知矩阵（CS 矩阵）。

假设M ≪N ，所以 y=Φx 是一个严重欠定的问题，而欠定问题在一般情况下没有唯一解，并且在有噪声干扰下，求解过程将会变得不稳定。上述方程可以通过l0范数最小化的方法求解，即

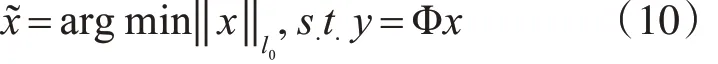
对于式（10），Donoho 和Chen 通过深入研究指出，在一定条件下，可采用lp范数代替l0范数，通常采用l1范数近似地对 x 的稀疏性进行约束［15］，此时式（10）变为

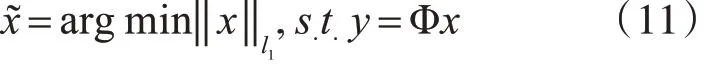
在实际中，观测噪声是不可避免的，需要引入加性噪声，即

由此可将式（11）修正为

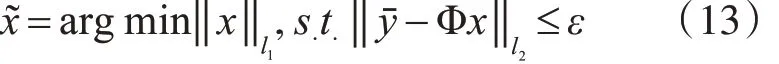
式中，ε 为与噪声有关的常量。

稀疏信号的重建问题是压缩感知的核心问题。目前有基于凸优化类算法、贪婪算法、组合重建算法和贝叶斯方法。本文采用基于凸优化类算法。所以式（13）变为

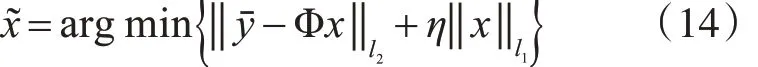
式中，η 为正则化参数，控制着信号x 稀疏度和允许误差之间的平衡。

4.2 基于压缩感知的声源强度描述

式（6）和式（12）具有相同的形式，式（6）的凸优化表达式为

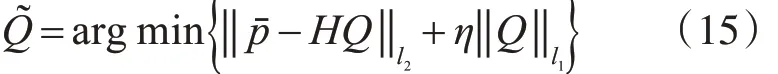
式（15）可以通过凸优化工具箱CVX 进行求解。而正则化参数η 是正确恢复信号的关键，文献［16］中给出了一个正则化参数计算公式为

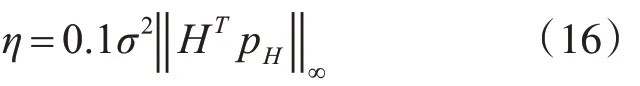
式中，σ2为归一化（信号功率为1）的噪声功率，‖‖HTpH∞为HTpH的无穷范数。

设式（16）中的0.1σ2=τ，则有

本文手动给定τ 的值，然后通过式（17）计算正则化参数η。

5 仿真实验与分析

由于等效源配置在声源面上，所以求得的声源强度就是声源面上每个网格点上实际声源强度的大小，声源强度较大的位置就是声源面上的主要噪声源所在的位置，本文仿真中采用平面传声器阵列接收含加性噪声的声压信号，研究对于声源面为平面且单声源位于全息孔径内外的噪声源分布效果。

5.1 单声源且声源位于全息孔径内

5.1.1 仿真条件

本文采用位于坐标(0,0,0) ，频率为1000Hz的点声源，介质密度为1000kg/m3，介质中的声速为1500m/s，全息面大小为1m×1m ，全息面网格点数为7×7，声源面大小为2m×2m，声源面网格点数为41×41，全息面与声源面之间的距离为0.5m。

5.1.2 仿真结果

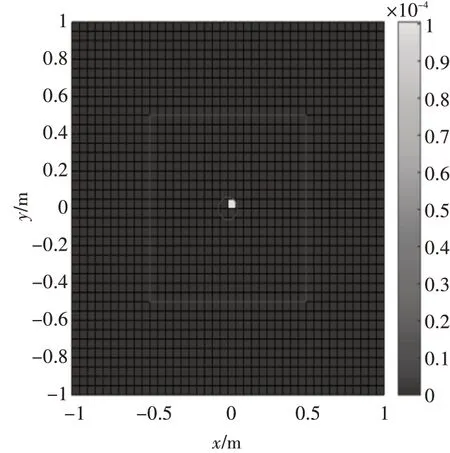
图1 理论噪声源分布

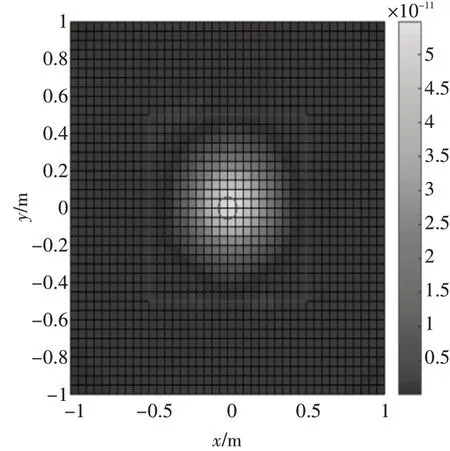
图2 实际噪声源分布（压缩感知，τ=0.01）

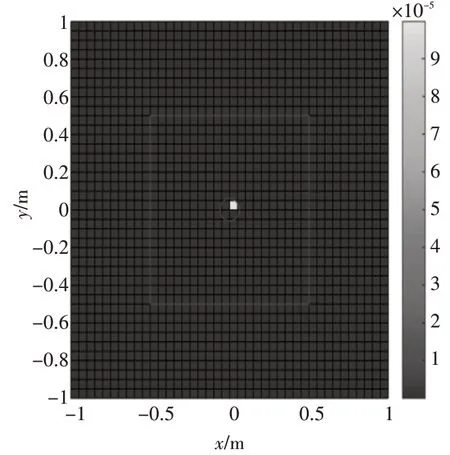
图3 实际噪声源分布（压缩感知，τ=0.001）

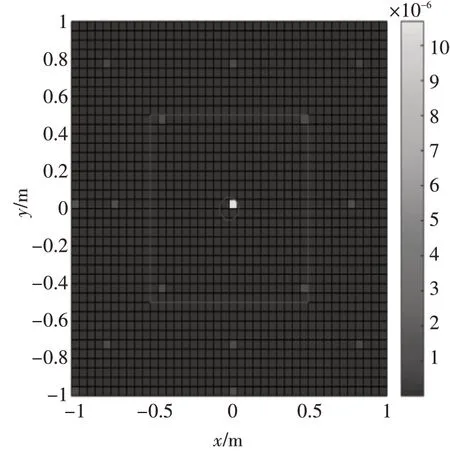
图4 实际噪声源分布（压缩感知，τ=0.00001）

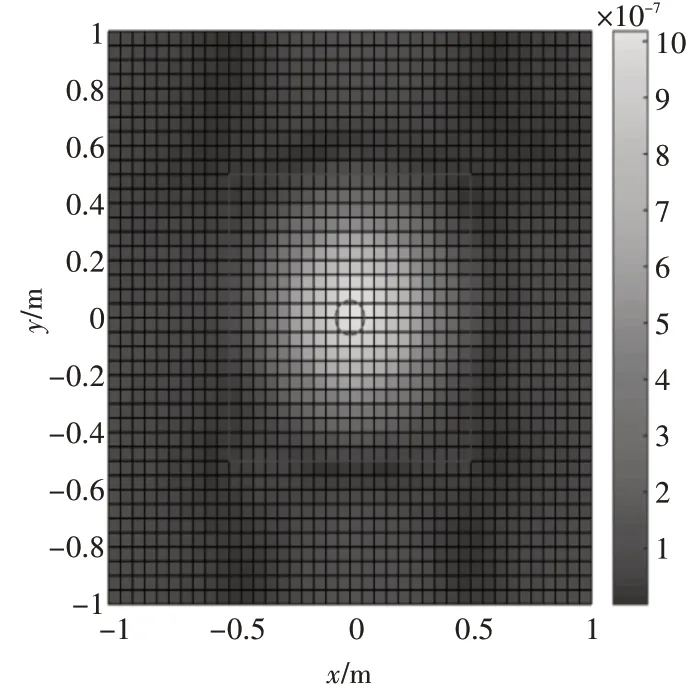
图5 实际噪声源分布（Tikhonov正则化，λ=2170727.2245）

5.1.3 仿真分析

从图2、图3、图4中可以看出，当τ 值取得较小（0.00001）时，由于不能很好地消除噪声的干扰，求解得到的声源强度会有较多的非零值，以致不能够很好地进行声源定位；当τ 值取得较大（0.01）时，虽然可以确定出真实点声源所在区域，但是求解得到的声源强度与真实值相差很大；当τ 取值合理（0.001）时，求解得到的声源强度与理论值才能符合得较好，获得了较好的声源定位效果。说明了对于单个声源且声源位于全息孔径内的共形问题，在τ 取值合理的情况下，即正则化参数取值合理，基于压缩感知的声源强度估计方法与理论值符合的较好，进而获得较好的声源定位效果。

从图3、图5中可以看出，通过压缩感知求解声源强度的方法比基于Tikhonov正则化方法求解声源强度精度高，这是因为传递矩阵对角占优和尽量对称这两个条件满足度较低，导致用正则化方法求解获得的声源强度并不能很好地匹配真实声场，使得基于等效源的近场声全息方法的噪声源识别与定位精度较低。结果表明，在对角占优和尽量对称两个条件满足度较低的情况下，通过运用压缩感知的方法，可以提高声源的分辨率，从而进行有效的声源定位。

5.2 单声源且声源位于全息孔径外

5.2.1 仿真条件

本文采用位于坐标(0.75,0,0)，频率为1000Hz的点声源，介质密度为1000kg/m3，介质中的声速为1500m/s，全息面大小为1m×1m，全息面网格点数为7×7，声源面大小为2m×2m，声源面网格点数为41×41，全息面与声源面之间的距离为0.5m。

5.2.2 仿真结果

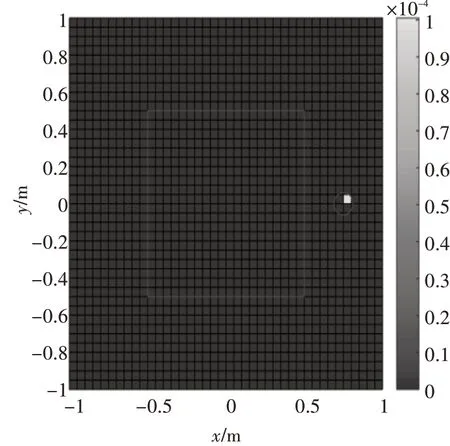
图6 理论噪声源分布

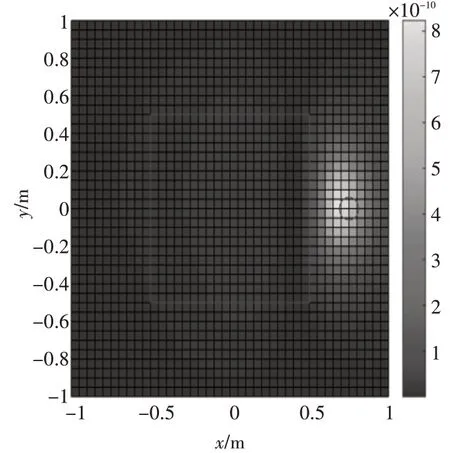
图7 实际噪声源分布（压缩感知，τ=0.01）

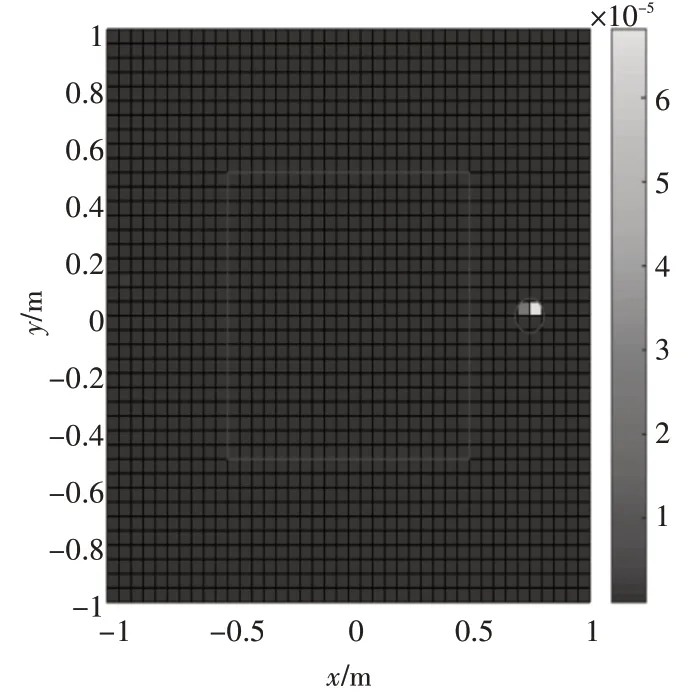
图8 实际噪声源分布（压缩感知，τ=0.001）

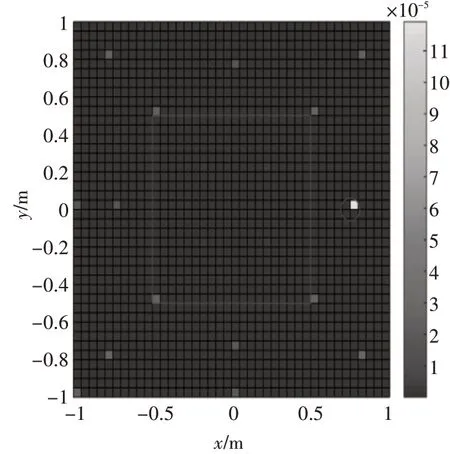
图9 实际噪声源分布（压缩感知，τ=0.00001）

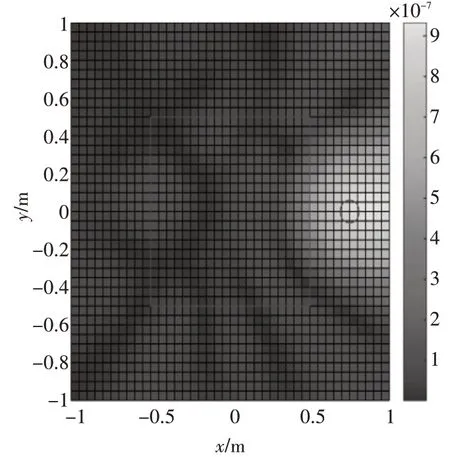
图10 实际噪声源分布（Tikhonov正则化，λ=1301188.0188）

5.2.3 仿真分析

从图7、图8、图9中可以看出，当τ 值取得较小（0.00001）时，不能很好地消除噪声的干扰，求解得到的声源强度有较多的非零值，无法进行声源定位。当τ 值取得较大（0.01）时，求解得到的声源强度与真实值相差很大，也无法进行声源定位。只有当τ 取值合理（0.001）时，求解得到的声源强度才能与理论值符合的较好，进而获得较好的声源定位效果。说明对于全息孔径外的单声源来说，在τ 取值合理时，通过压缩感知求解得到的声源强度与理论值符合的较好，进而获得较好的声源定位效果。

从图8、图10 中可以看出，对于单声源位于全息孔径之外，通过压缩感知求解声源强度的方法比基于Tikhonov正则化方法求解声源强度精度高，这还是因为传递矩阵对于对角占优和尽量对称这两个条件满足度较低，导致用正则化方法求解获得的声源强度并不能很好地匹配真实声场，使得基于等效源的近场声全息方法的噪声源识别与定位精度较低。结果表明，在对角占优和尽量对称两个条件满足度较低的情况下，通过运用压缩感知的方法，可以提高声源的重建精度，从而获得良好的声源定位效果。

从图3、图8中可以看出，单声源位于全息孔径内的噪声源识别与定位比单声源位于全息孔径外的噪声源识别与定位精度高。这是因为单声源位于全息孔径外时，全息面测量得到的声场信息出现“泄露”现象，使得声源识别与定位效果变差，从而导致噪声源的分辨率降低。结果表明，要想获得良好的噪声源识别与定位效果，有较高的声源分辨率，就必须使得噪声源尽量在全息孔径之内。

6 结语

本文提出了一种基于压缩感知和等效源的近场声全息方法的噪声源识别与定位算法。该算法在传递矩阵对角占优和尽量对称满足度较低的情况下，通过把声源强度的求解问题转化为稀疏信号的重建问题，并通过凸优化类算法求得正则化参数，并分析了单声源位于全息孔径内外噪声源识别与定位问题。仿真结果表明，本文的算法比基于Tikhonov 正则化算法重建精度高，并且单声源位于全息孔径内比单声源位于全息孔径外噪声源的分辨率高。从而对于单声源位于全息孔径外，提高噪声源的重建精度还有待进一步研究。