基于诱导有序加权平均算法的风电场短期功率的预测

王硕禾,陈祖成,张国驹2,刘治聪

(1. 石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043；2. 新疆金风科技股份有限公司，新疆 乌鲁木齐 830026)

风电功率预测根据预测物理量可以分为功率直接预测和功率间接预测方法。根据不同的统计模型又可分为持续输出法、支持向量机(support vector machine，SVM)模型[1-2]、自回归滑动平均(auto-regressive and moving average，ARMA)法[3]、卡尔曼滤波法[4]和神经网络法[5-6]等。

近年来，许多学者对风电场功率预测进行了研究，并且取得了一定的成果。文献[7]中采用小波-反向传播(back propagation，BP)神经网络预测模型对风电场功率进行预测，该模型利用小波函数将风速和功率在一定尺度上进行分解，并使用多个BP神经网络对各频率分量进行预测，最后通过重构得到预测结果，从一定程度上提高了预测精度，但是单一预测模型具有一定的局限性，并非现在风电场功率预测的趋势。文献[8]中采用的组合预测方法是基于历史数据的基础上如何选取合适的单一预测模型并进行组合，从而提高预测精度。文献[9]中基于电力消费量的历史数据提出了诱导有序加权平均(induced ordered weighted averaging，IOWA)组合预测算法，从而提高了预测精度，但是该算法在进行组合预测之前并没有对单一预测模型进行冗余性分析，可能造成效率低、结构复杂等问题。文献[10]中采用信息熵原理方法计算单一预测模型的权重系数，进而将单一预测模型进行组合预测，提高了预测精度，但是该方法没有对单一预测模型进行检验和判定其适用性，虽然提高了预测精度，但是仍存在一些缺陷。

文献[11]中提出一种改进的神经网络结构和最佳权重的训练方法，利用可信技术(trust-tech)深度搜索优质子区域，可以得到不同子区域下的最有权重解，进而提高了预测精度。本文中基于IOWA算法对风电场的功率进行预测，该方法通过对优选单一预测模型在样本区间上各个时刻点的预测精度的高低按顺序赋予其权重系数，进而构造拉格朗日乘数法求解出唯一的最优权值向量，然后以误差平方和最小值为目标函数建立组合预测模型，优选单一预测模型的方法是误差信息矩阵法。本文中根据华北某风电场的功率数据和气象数据建立了7种单一预测模型，并从中优选出4种模型，利用IOWA算法进行组合预测，以验证预测结果的准确性。

1 基于诱导有序加权平均算法的组合预测模型

1.1 误差信息矩阵

如果用Yt表示t时刻风电场功率组合模型预测值，wi表示第i个预测模型的权重系数，那么k种预测模型的风电场功率组合预测值为

(1)

预测值相对误差为

et=yt-Yt。

(2)

预测误差平方和为

(3)

(4)

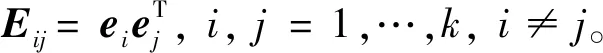
1.2 IOWA算法基本原理

IOWA算法的基本原理是通过每个时刻预测出来的值计算该时刻的精度大小，按照精度从大到小的顺序赋予各个单一模型权重系数，然后以预测值和实际值构造误差平方和函数，以最小值为目标建立组合预测模型。这种方法的特点是得到的权重系数仅仅与各单一模型的预测精度大小有关，而与是何种预测模型无关。

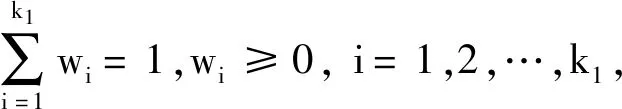
(5)

这里假设第i种模型在第t时刻的预测精度为ait，则有

(6)

式中ait∈(0,1)。

如果把ait作为预测值yit的诱导值，那么k1种单一预测模型在第t时刻的预测精度和预测值构成了k1个二维数组(〈a1t,y1t〉,〈a2t,y2t〉,…,〈ak1t,yk1t〉)。ait是预测值yit排序的诱导值，将k1种单一模型在第t时刻的预测精度a1t,a2t,…,ait,…,ak1t按照从大到小的顺序重新进行排列，那么根据此序列产生的基于IOWA算法的组合预测值表示为

(7)

式中a(it)为第t时刻第i大的预测精度的下标。

式(5)、(7)这2个式子的根本区别是权重系数与单一预测模型的种类无关，而是与单一预测模型在各个时刻预测精度的大小密切相关，这是基于IOWA算法组合预测模型的重要特征。

令ea(it)=yt-ya(it)，那么n时刻总的组合预测误差的平方和为

(8)

那么以误差平方和为目标函数，采用IOWA算法的风电场功率预测组合预测模型的最优化可以表示为

(9)

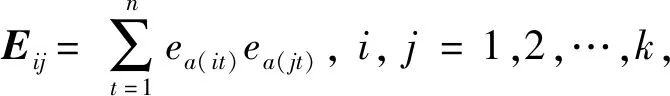
minS(w)=wTEw，

(10)

式中R=(11…1)T是k1×1维列向量。

因为矩阵E是正定矩阵，所以根据正定矩阵的定义，E的逆矩阵E-1存在并且也是正定矩阵，风电功率预测组合预测模型下的权重向量具有非负性，即权重系数大于等于零，则式(10)转换为

minS(w)=wTEw，

(11)

s.t.RTw=1 。

由于误差信息矩阵E和其逆矩阵E-1都是正定矩阵，构造拉格朗日函数为S(w)=wTEw+λ(RTw-1)，λ是拉格朗日乘子。根据极值的必要条件(如果函数S(w)取得极值，则S(w)的偏导数在极值点必然为零)，分别令∂S(w)/∂w=0和∂S(w)/∂λ=0，即有

(12)

可得模型的解为

(13)

因为

(14)

式中λi(i=1,…,k)是误差信息矩阵E的特征值，λi>0，所以E1是正定矩阵，E1>0，则函数S(w)为严格的凸函数[12]。综上，式(13)为函数S(w)的唯一最优解。

虽然通过IOWA算法得到组合预测模型的最优解，但是单一预测模型众多，如果模型选择不合理，可能会降低预测精度。选取合适的单一预测模型是组合预测的关键问题之一，因此应当根据误差信息矩阵原理选取合适的预测模型[13-17]。

2 基于误差信息矩阵的择优方法

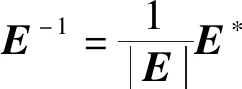
(15)

式中E*是E的伴随矩阵。

因为E和E-1都是正定矩阵，所以伴随矩阵E*也是正定矩阵。对任意的维非零向量R≠0，有f(x)=RTE*R>0，称为f(x)正定二次型，所以E*R>0，即

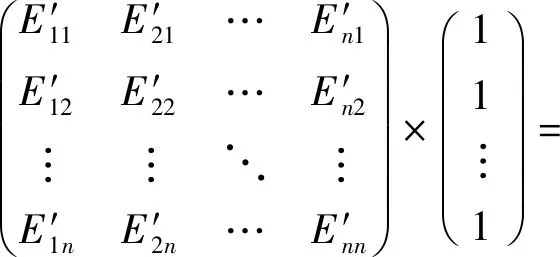
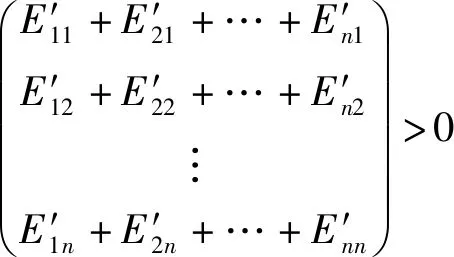
(16)

因为伴随矩阵中的每个元素都是对应该元素的代数余子式，所以只要误差信息矩阵中对应的每列(行)元素的代数余子式之和大于零，那么对应的该单一模型为优选模型。

然而，当参与的优选单一模型种类较多的时候，算法和结构变得复杂，并且计算量加大，计算机运行时间长、效率低，因此，为了提高效率，应进行多模型组合。IOWA算法的求解过程可以采用第3节的方法进行优化，并利用IOWA算法的特征对单一模型进行组合，建立风电场短期功率组合预测模型[18-20]。

3 诱导有序加权平均算法的优化与优化模型的建立

针对该算法可能因单一预测模型种类多而带来的复杂性，利用以下内容对该算法进行优化，以简化该算法，提高运算效率。第一步是构造诱导矩阵Y1=YD,则

(17)

式中：k为预测模型的种类；n为时刻。矩阵中的每一行的元素表示在第t时刻(t=1,2,…,n)每种预测模型的预测精度与相应预测值组成的元素数组。

利用IOWA算法诱导有序的重要特征，对诱导矩阵Y1中的每一行根据诱导值aij按照大到小的顺序重新排列，得到诱导有序矩阵

Y2=YX=

(18)

将YX拆分为矩阵A和矩阵Y′ 2个矩阵，

(19)

式中：A是以排序后的诱导值为元素构成的矩阵；aij表示经过排序后在第i个时刻顺序为j的预测精度(i=1,2,…,n;j=1,2,…,k1)；Y′表示与矩阵A相对应的各个诱导值为元素的预测值矩阵；yij表示根据诱导值重新排列后的第i个时刻顺序为j的预测值。

令y=(y1,y2,…,yn)T，w=(w1,w2,…,wk1)T，那么以预测误差平方和最小目标函数的基于IOWA算法组合预测模型表示为

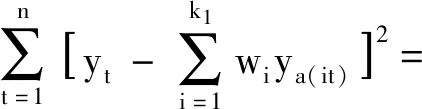
(y-Y′w)T(y-Y′w)。

(20)

由式(20)得最优化模型为

minS(w)=(y-Y′w)T(y-Y′w)，

(21)

当该风电场短期功率组合预测模型的种类比较多时采用MATLAB软件可以相对容易地求解出模型的最优权重系数，即组合权重向量w0。

综上，利用IOWA算法优化求解组合权重的流程如图1所示。

图1 风电场功率组合预测模型流程图

4 风电场功率的组合预测研究

基于以上误差信息矩阵法，本文中采用了BP神经网络、径向基(radial basis function，RBF)神经网络、Elman神经网络、SVM、小波神经网络、小波-SVM模型、粒子群优化(particle swarm optimization，PSO)的SVM模型等7种单一预测模型，数据采用华北某风电场2017-05-01—10-30的历史风电功率数据和对应的数值天气预报的数据(包含风速、风向、温度和湿度)，采集频率为15 min，每天96个点，一共含有17 368个数据点。用2017-05-01—10-28的数据作为训练数据，2017-10-29—30的数据作为预测数据，搭建各个单一预测模型，把采集到的数据经过预处理后作为输入向量输入到各个预测模型中得到预测功率，进而得到预测误差，最终得到误差信息矩阵

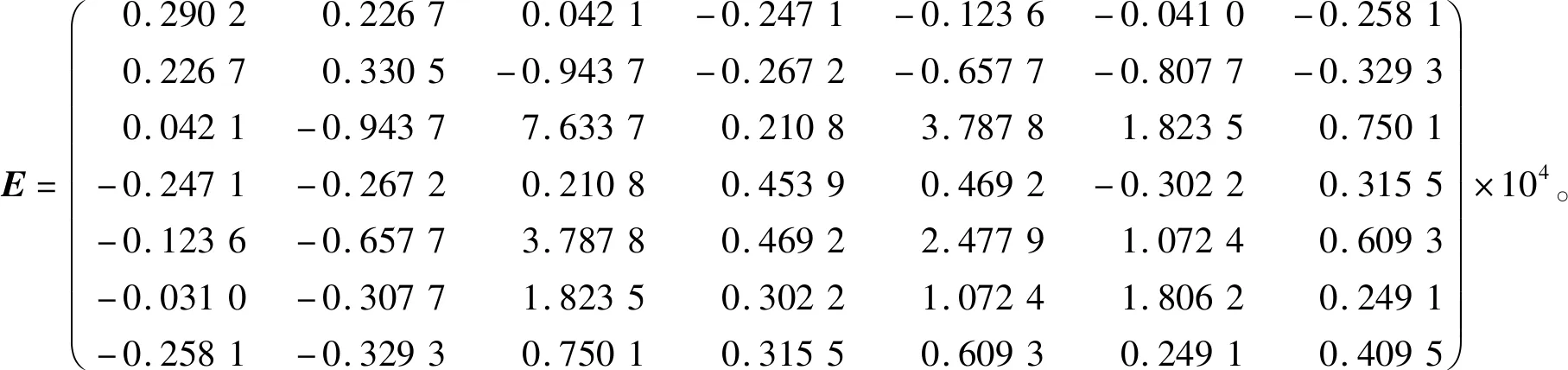
计算上述误差信息矩阵的伴随矩阵，得到

由伴随矩阵的定义

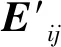
图2 风电场功率组合预测效果

图3 风电场功率组合预测绝对误差

通过对图2、3的分析得知，基于IOWA算法的风电场功率预测的预测值与实际值之间的误差很小，精确度高，原因是IOWA算法的原理与单一预测模型没有关系，而是与各个单一模型在特定时刻的预测精度的大小有关，在特定时刻预测精度越高，权重系数也就越大。为了具体说明该模型的有效性，将去除冗余模型的组合模型与未去除冗余模型的模型进行对比，2种模型的误差评价指标如表1、2所示。

由表中数据可知：1)针对该风电场的历史功率数据和数值天气预报数据，单一预测模型中BP神经网络、Elman网络、SVM和小波-BP模型的预测精度较高，更适用于该风电场功率预测；2)去冗余模型之后的IOWA算法组合模型的预测准确率明显高于单一预测模型，证明该方法的有效性；3)未去冗余模型的IOWA算法组合预测模型的预测精度相对于一部分模型预测精度有所提升，但并不是高于所有单一预测模型，说明并不是单一预测模型种类越多，组合预测模型的预测精度越高，说明组合预测模型对单一预测模型是有选择性的；4)去冗余模型之后的IOWA算法组合预测模型的预测精度要高于未去除冗余模型的组合预测模型，说明去冗余模型之后的IOWA算法组合预测模型的精度高，效果好。此外，单一预测模型减少，使得预测模型结构的复杂性降低，缩短了预测时间，提升了预测效率，这是目前风电场功率预测所要求的。

表1 去冗余模型之后的组合模型的误差评价指标

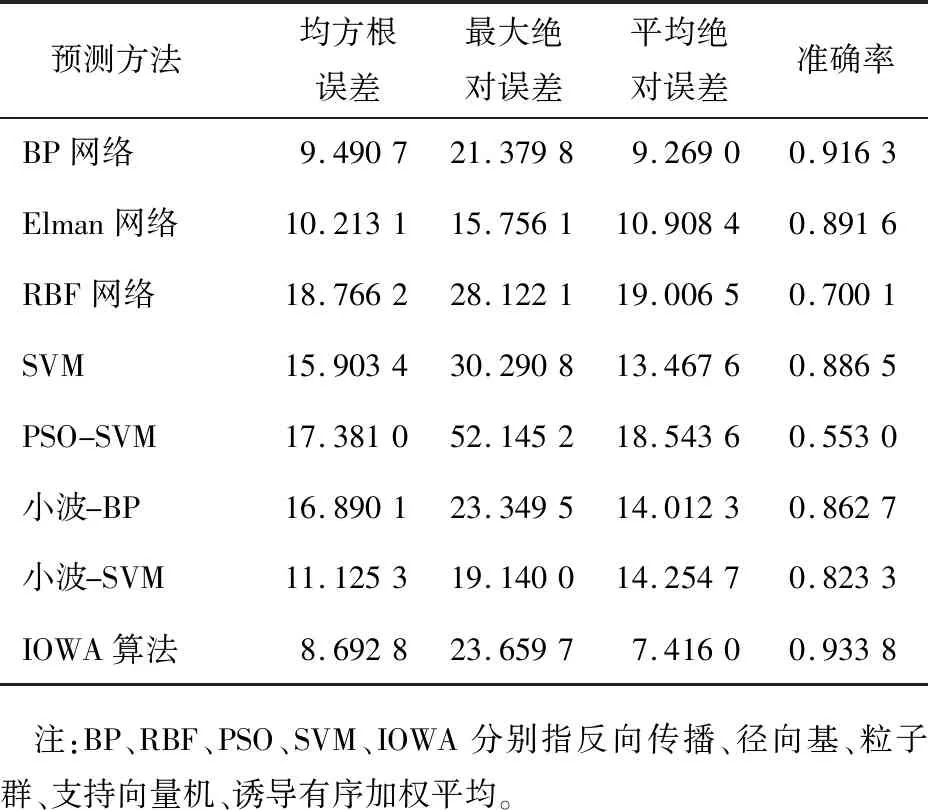
表2 未去冗余模型的组合模型的误差评价指标

5 结语

本文中通过对风电场功率短期预测模型的研究，提出了一种基于IOWA算法风电场功率组合预测模型。为了提高该算法的预测精度和效率，首先对参与预测的单一预测模型进行冗余性分析，剔除掉冗余模型后，以优选模型的预测精度为诱导因子，按照从大到小的顺序进行排序，以排序之后的对应的各个时刻的预测值建立预测误差平方和函数，进而求出权重向量。该方法的优点在于权重系数的选取与模型在各个时刻的预测精度大小密切相关，可以充分利用单一模型的预测结果，优化信息利用率，提高预测精度和效率，具有一定的实用价值。