基于平行竞争PSO算法的土壤水分测量研究

刘云潺，张慧宁

(黄河水利职业技术学院，河南 开封 475004)

在节水灌溉中，需要对农田土壤水分情况进行测量[1]。人工监测，既耗费人力，又不能实时监控，因此通过土壤水分特征曲线描述土壤含水量与吸力之间的关系，对于研究土壤水分特征十分重要[2]。

土壤水分测量与土壤本身的机理无关，最著名的是Van Genuchten模型，模型中参数的物理意义明确且与实测曲线拟合较好[3]，但是Van Genuchten模型属于非线性复杂方程并且参数较多，拟合参数过程属于非线性问题，若使用线性方法和线性拟合会出现较大误差。目前解决方法有：最小二乘法(Least Square Method，LSM)拟合Van Genuchten模型方程参数[4]，能够对参数的求解提供较好的方法，但是会遇到求解停止或参数为负的问题；粒子群算法(Particle Swarm Optimization,PSO)，编程简单[5]，但是在Van Genuchten模型参数寻优后期容易产生停滞现象；差异进化粒子群算法(Differential Evolution PSO,DEPSO)，考虑了多参数间的相关性，能够在一定程度上简化方程参数估计[6]；模拟退火算法(Simulated Annealing,SA)、遗传算法(Genetic Algorithm,GA)，均能够获得参数解[7,8]，但全局收敛性相对较弱。

本文引入平行、竞争策略，提出平行竞争PSO算法(Parallel Competition PSO，PCPSO)，竞争机制通过更新部分粒子来改善群体的多样性同时保持最好的粒子，最差粒子被重置；平行策略通过把粒子群分成若干子群，引入共享因子对子群之间信息共享进行动态调节，实验仿真显示本文算法对测试函数求解具有收敛速度较快、解精度较高的特点，测量粉壤土水分的相对误差相比其他算法都较小。

1 改进PSO算法

1.1 基本PSO算法

粒子群算法(Particle Swarm Optimization，PSO)通过学习因子c1和c2及惯性权重ω进行更新速度vq,h和位置xq,h[9]:

(1)

式中：q=1,2,…，h=1,2,…，t为迭代次数；xq,h(t)为第q个粒子在第t次迭代时第 维的位置；vq,h(t)为第q个粒子在第t次迭代时第 维的速度；pg,h为历史最优值；pq,h为当前最优值；r1∈(0,1)、r2∈(0,1)为相互独立的随机函数。

1.2 基于平行竞争的PSO算法

经典粒子群优化算法存在早熟收敛和停滞现象，因为当评价函数高维或者形状复杂，粒子最终被困在一个局部极小值范围内。

1.2.1 竞争机制

通过更新部分粒子来改善群体的多样性同时保持最好的粒子，最差粒子被重置，以便更好地探索Van Genuchten模型参数[10]。新生成的粒子将试图寻找更好的最优值，这样最好的粒子围绕当前的全局最佳位置保持搜索。如果最新的粒子找到更好的最优值，粒子群就会聚集在全局最佳周围，否则它们将回到当前全局最佳状态，直到再次被重置。只有粒子在检测到早熟收敛时才被触发重置，这样粒子群获得了内部竞争。粒子状态检测到需要重置的方法如下：在第t次迭代时，如果粒子群最大半径值δt小于阈值ε时，竞争才被触发。ε表达式根据经验确定，不但对于控制竞争触发效果要求较高，而且要阻止群体中任何粒子在局部最小值中停滞太久。最终δt与ε设计为：

(2)

式中：‖‖为欧几里得范数；s为粒子总数。

粒子被重置的比例应该随着迭代次数增加而减少，不应该一直以一定的规模被重置，因此通过非线性策略，粒子在迭代t上由Logistic函数σ(t)重新设置比例，σ(t)减少与迭代次数的线性相关性。通过引入一个竞争性参数γ∈[0,2]控制：

(3)

Logistic函数 与不同的 值关系如图1所示。

图1 σ(t)与不同的γ值Fig.1 σ(t)and different γ values

通过图1可以发现，当γ值较大时，有助于增加粒子之间的竞争，但是收敛较慢；当γ值较小时，粒子之间的竞争减弱，但是收敛较快，γ=0时，不存在竞争性。本文令γ=1，这样可以保持竞争性同时加快收敛速度。

1.2.2 平行策略

粒子之间的搜索信息交流采用平行子群方式[11,12]，把粒子群分成若干子群，子群的群平均适应度与原始粒子群平均适应度相差不能小于设定的阈值ζ，每个子群由若干个粒子构成。ζ计算为：

(4)

(5)

(6)

式中：fn为各个子群的适应度值；f为归一化因子，调节ζ大小。

在搜索过程中，为了控制粒子个体之间信息共享的程度，实现子群中较差个体的更新，引入共享因子对子群之间信息共享进行动态调节，任一个子群中的粒子与周围子群信息共享次数为e1∈[1,E]，E为最大共享总次数，共享因子ψ1计算为：

(7)

子群中的粒子与自身子群信息共享次数为e2∈[1,E′]，E′为最大共享总次数，共享因子ψ2计算为：

(8)

(9)

式中：s为sigmoid 型隶属函数。

sigmoid 型隶属函数控制共享过程如图2所示。

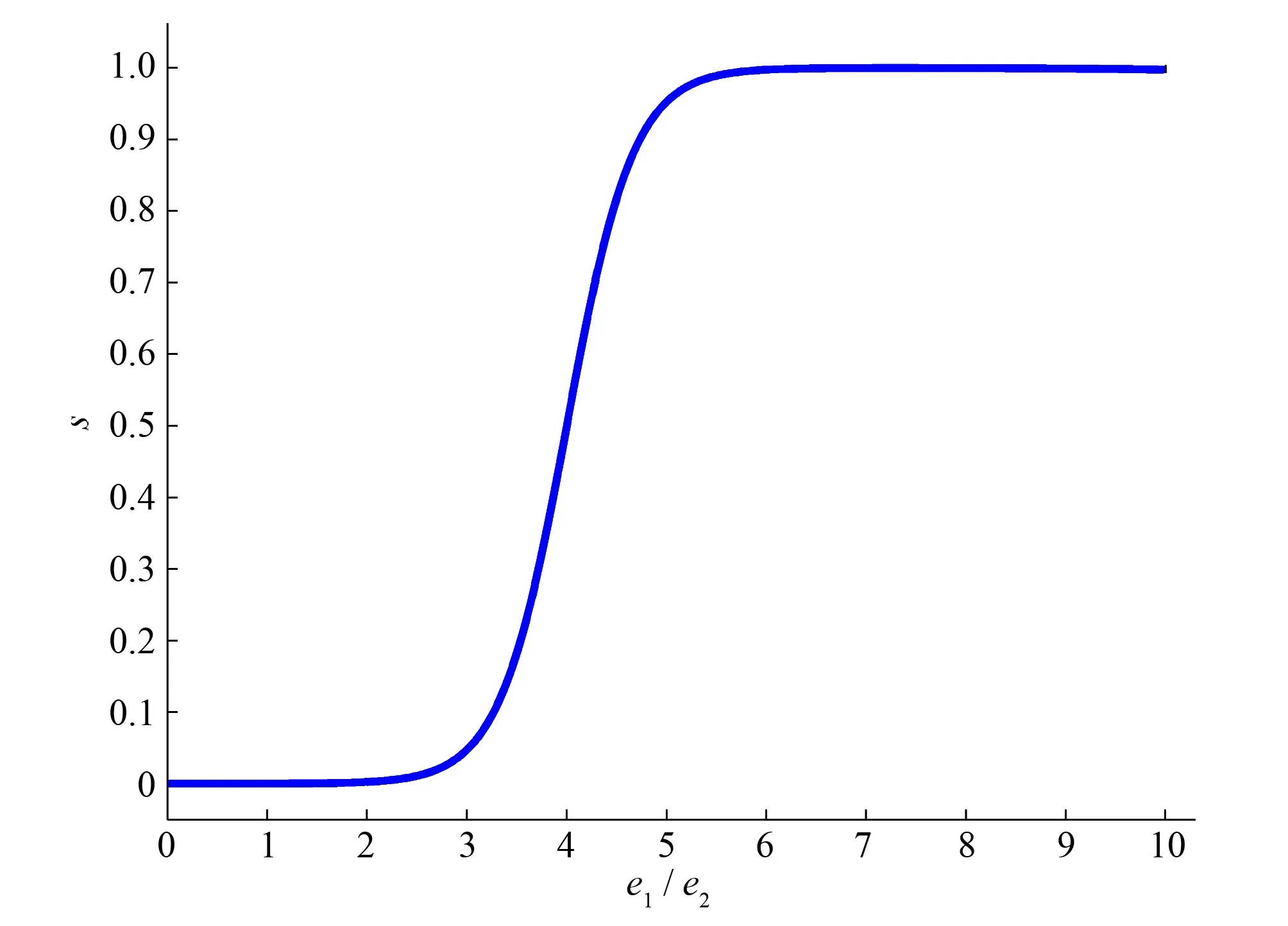
图2 sigmoid 型隶属函数控制共享过程Fig.2 Sigmoid type membership function controls sharing process

从图2可以看出，e1/e2较小时寻优前期共享主要在自身子群中进行；当e1/e2达到一定程度时，s迅速增大，共享寻优主要与周围子群进行，扩大搜索范围，避免局部解。

则粒子更新速度vq,h和位置xq,h为:

(10)

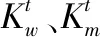
2 土壤水分测量模型

土壤水分特征曲线Van Genuchten模型为：

(11)

式中:θ为土壤体积含水量，cm3/cm3；h为土壤基质势，cm；θr和θs分别为土壤的剩余体积含水量和饱和体积含水量，cm3/cm3；a和n均为经验拟合参数,m=1-1/n。

参数θs、θr、a、n相互独立，确定需要优化变量的取值范围θs∈[0,0.6]、θr∈[0,0.3]、a∈[0,1]、n∈[1,10]。但是由于方程的参数较多，常规的线性处理与线性拟合无法真实实现数据曲线，需要通过非线性拟合方法实现[13-15]。

把均方误差作为Van Genuchten方程曲线拟合度评价标准：

(12)

则粒子群适应度函数f(h)选择为：

(13)

当f(h)获得最小的时候则Van Genuchten方程曲线拟合度较高。

算法流程：①粒子群初始化，产生粒子个体；②计算粒子的适应度；③按照公式(2)、(3)进行竞争操作；④按照公式(7)、(8)进行平行子群操作；⑤按照公式(10)更新粒子群；⑥若满足最大迭代次数或Van Genuchten方程曲线拟合度，精度控制在10-6，满足进行步骤⑦，否则进行步骤②；⑦输出θs、θr、a、n参数值。

3 实验仿真

实验PC配置为CPU3.6GHz、内存8GB，集成显卡，Matlab2014编程实现仿真，粒子群设置为400个，最大迭代次数为300，子群数量最大为20个，c1=c2=2，ω∈(0.2,0.8)。测量土壤水分传感器采用时域反射型，探针长度：8.5 cm，探针直径：3 mm，密封材料：环氧树脂，探针材料：304不锈钢。

3.1 算法性能分析

为了检测PCPSO算法的性能，选择4个复杂函数Sphere function、Rosenbrock function、Rastrigin function、Quartic function进行测试，分别如下：

图3至图6给出了4个测试函数求解过程中平均最优值的变化曲线。

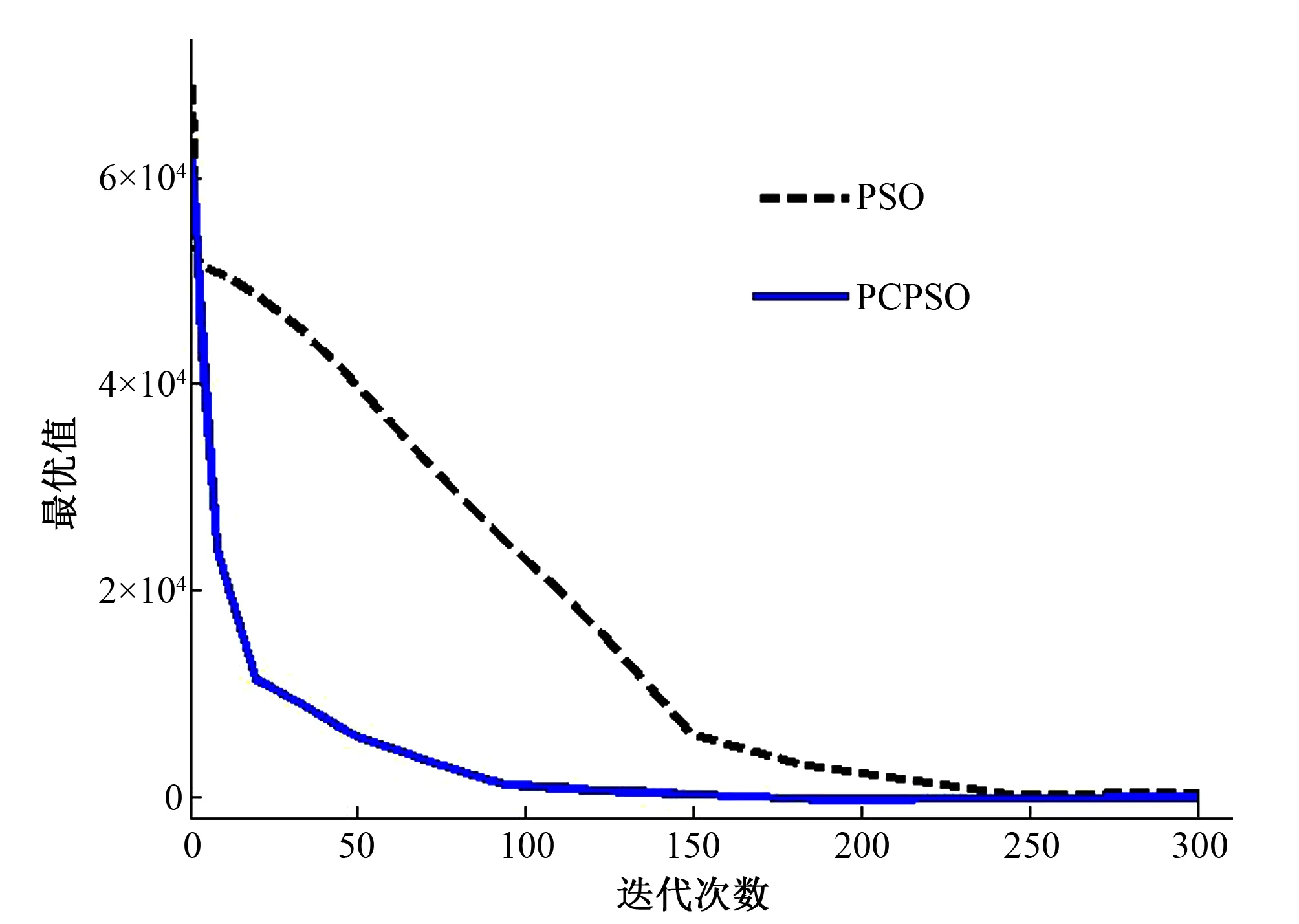
图3 Sphere function 变化曲线Fig.3 Sphere function variation curve

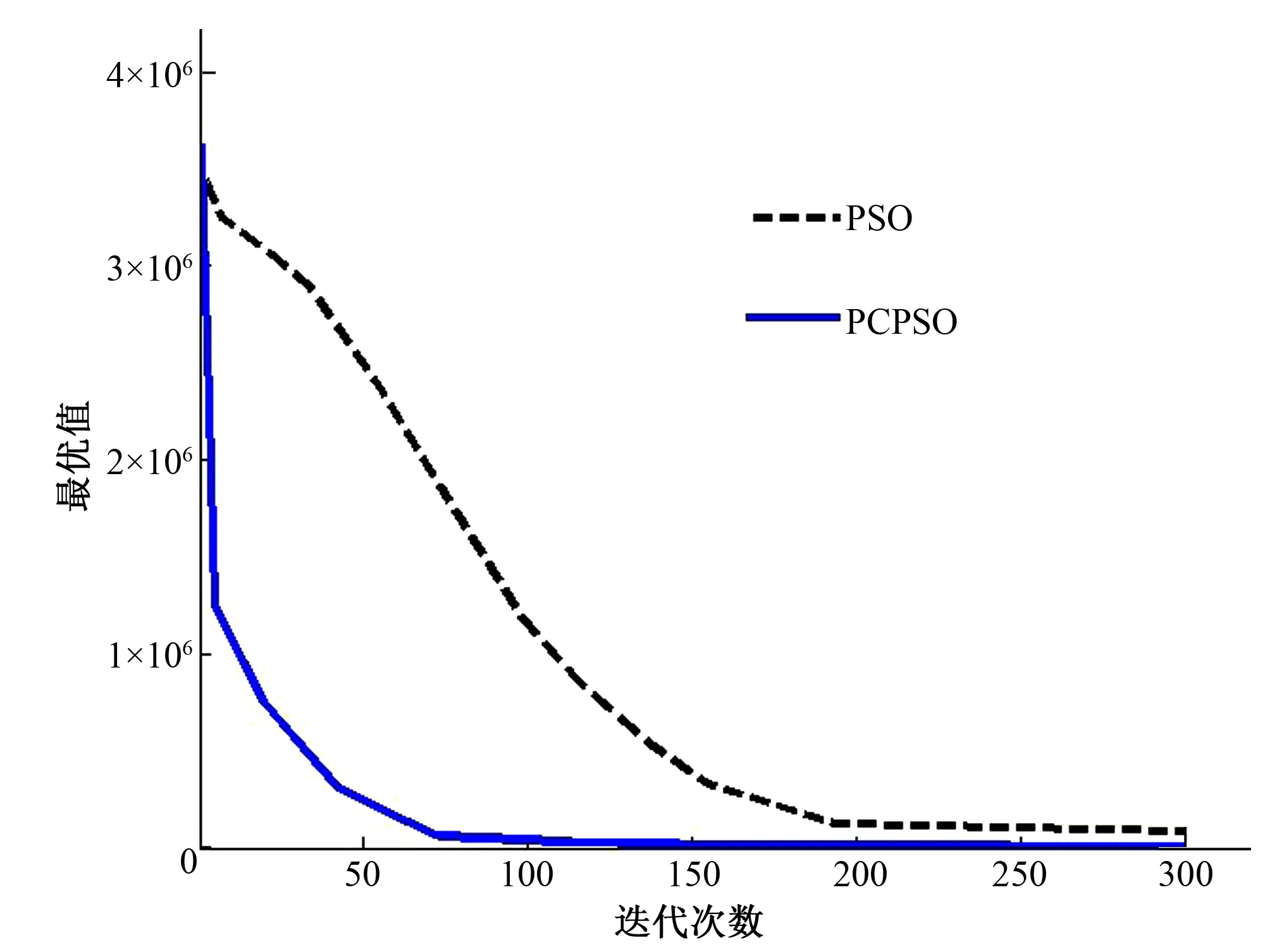
图4 Rosenbrock function变化曲线Fig.4 Rosenbrock function variation curve

图5 Rastrigin function 变化曲线Fig.5 Rastrigin function variation curve

从图3至图6可以看出PCPSO算法仿真实验结果较好,PCPSO算法对测试函数都能搜索到比PSO更优的结果，收敛速度较快，同时解的精度较高。这是因为PCPSO算法在迭代过程中，通过阈值 触发竞争机制保持适应度值较大的粒子优势，避免早熟，平行策略向全局最优位置收敛，进而使得方程解优化达到最优。

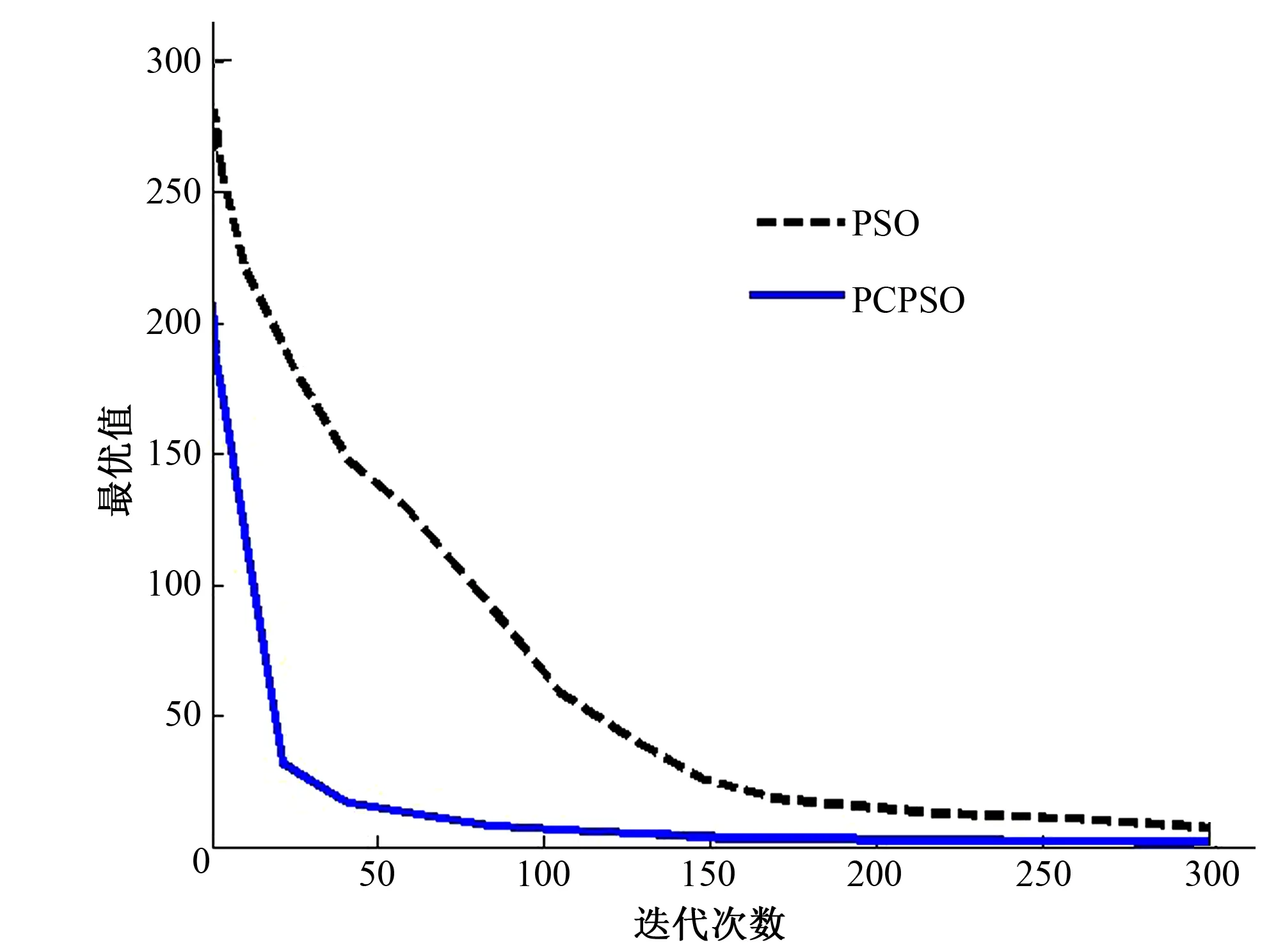
图6 Quartic function 变化曲线Fig.6 Quartic function variation curve

3.2 土壤水分测量分析

在求解粉壤土Van Genuchten模型参数过程中，使用了LSM、PSO、DEPSO、SA 、GA、PCPSO方法，实验中每个算法采用蒙特卡罗方法法独立运行30次，结果取平均值获得参数解如表1所示。

对粉壤土进行不同算法模拟数据与实测数据对比如表2所示。

根据表1获得的θs、θr、a、n参数值，从表2可以看出，本文算法对粉壤土模拟数据接近实测数据。不同方法对粉壤土脱湿、吸湿θ～h实测数据的相对误差比较如图7和图8所示。

表1 不同方法确定粉壤土Van Genuchten模型参数Tab.1 Determination of Van Genuchten model parameters for silt loam by different methods

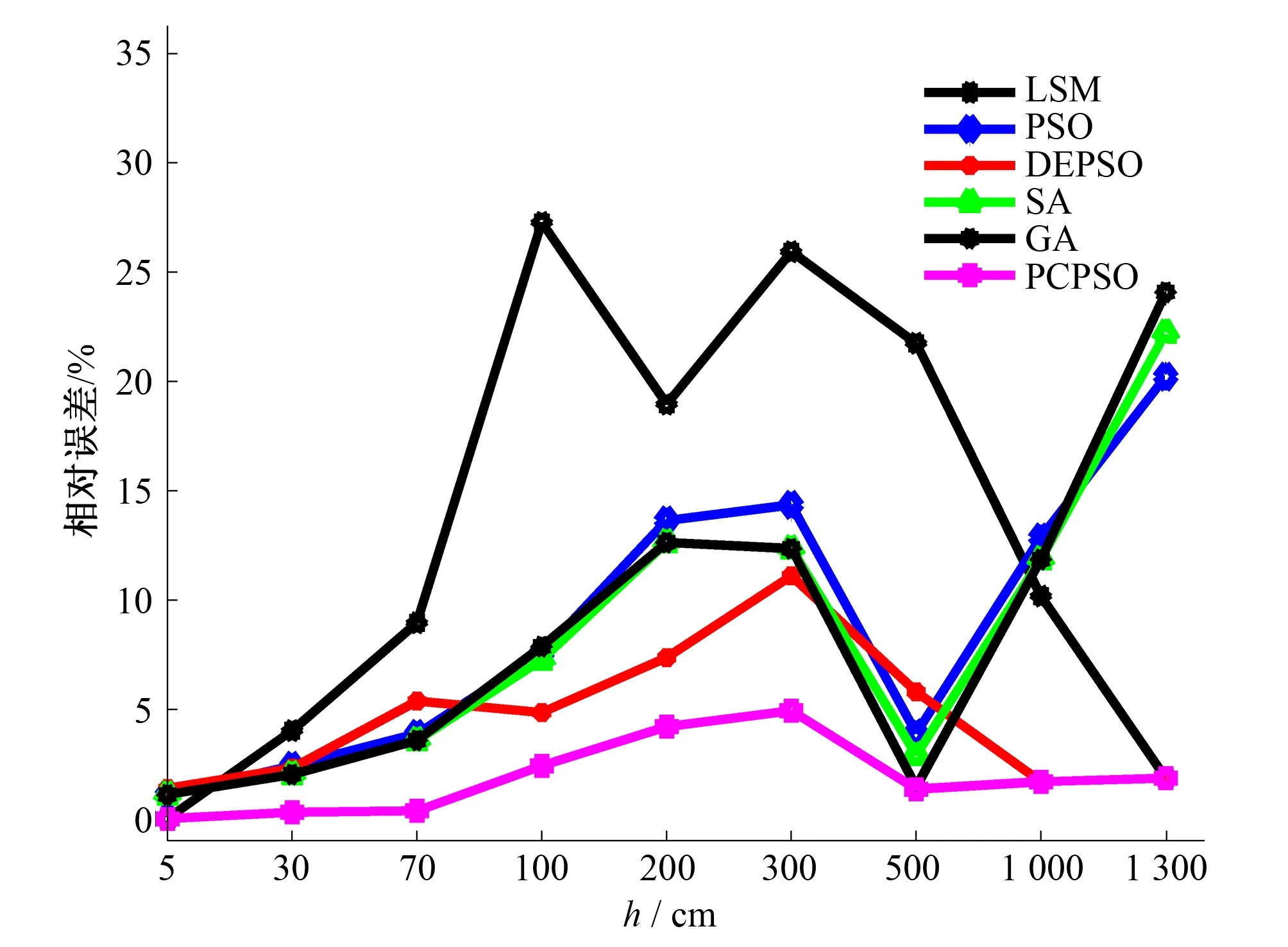
图7 不同方法对粉壤土脱湿θ～h实测数据的相对误差比较Fig.7 Comparison of relative error of θ～h measured by different methods for silt loam dehumidification soil

从图7和图8可以看出，本文PCPSO算法对粉壤土脱湿、吸湿θ～h实测数据相对误差比较小，脱湿实测数据相对误差最大为5%，吸湿实测数据相对误差最大为4%，其他算法都比PCPSO大，从而在实际测试中会导致较大的误差。这是因为PCPSO算法在可行解空间内通过多个子群从多个初始解开始搜索,而竞争策略防止搜索过程收敛于局部最优解，从而获得全局最优解。

表2 不同方法模拟粉壤土θ～h数据与实测数据对比 cmTab.2 Comparison of θ～h data and measured data for different methods of simulating loam soil

图8 不同方法对粉壤土吸湿θ～h实测数据的相对误差比较Fig.8 Comparison of relative error of θ～h measured by different methods for silt loam absorption soil

4 结 语

本文提出平行竞争策略PSO算法，竞争机制更新最差的粒子，平行策略引入共享因子对子群之间信息共享进行动态调节，实验仿真显示本文算法对测试函数求解具有收敛速度较快、解精度较高的特点，模拟测量粉壤土水分的相对误差相比其他算法都较小，因此为测量土壤水分提供了一种新方法。