基于改进的BP神经网络对蓄水坑灌冬季果园土壤温度预测

贺琦琦，郭向红，雷 涛，王晓磊，孙西欢,2，马娟娟，张少文，刘艳武

(1.太原理工大学水利科学与工程学院，太原 030024；2.晋中学院，山西 晋中 030600)

0 引 言

蓄水坑灌法具有节水、保水、抗旱等优点，是一种适合我国北方干旱地区的果林灌水方法，并能有效的缓解水土流失[1,2]。该灌溉方法是在果树树干周围挖取圆柱形小蓄水坑，往坑内注水进行灌溉。采用蓄水坑灌进行灌溉，土壤水分会集中分布于40～160 cm间的土层中，有利于根系吸水[3]。但是，蓄水坑增加了果树根部土壤与空气的接触面积，导致冬季果树根部土壤温度明显降低，对果树的生长发育极为不利。针对这种现状，一些学者针对不同覆盖方式和不同蓄水坑结构研究了蓄水坑灌条件下土壤温度的分布特征[4,5]。但是，这些研究都趋向于对土壤温度定性研究，在定量研究方面还有待加强。

土壤温度的预测预报模型大体可分为机理模型和经验模型。机理模型，也称“白箱模型”，是一种基于平衡方程和定律而建立的精确数学模型，模型需要的数据少，但是数学表达式的建立比较困难，所需的参数较多而且难以确定。经验模型包括传统的统计回归模型和神经网络模型。回归模型是通过对数据的统计分析，找出与数据拟合最好的模型，它的缺点是对于因子的选择和表达不好确定；神经网络模型，又称“黑箱模型”，是根据输入和输出的关系建立起来的模型，不需要考虑中间的过程，而是把实测的与过程有关的数据进行数理统计分析，并根据误差最小的原则总结出变量与参数间的数学表达式。经验模型需要的数据量大，要求具有较高可靠性的输入项，结构较为简单，参数较少，因此得到了广泛的应用，但是不适用于不可测输入的过程。利用黑箱模型对土壤温度变化进行预测的研究在国内外已经有很多的报道，大多集中在分析各个气象因子与土壤温度的显著性关系，并由此建立模型对土壤温度的变化进行预测[6-8]。BP神经网络是当前应用较为广泛的一种黑箱模型，其结构相对简单，王晓磊[9]研究了BP神经网络对蓄水坑灌冬季土壤温度分布的预测，但是BP神经网络生成的初始权值和阈值随机性很强，当网络存在较多极小值时容易达到局部最优，不能取得全局最优解，而且对收敛速度也有很大的影响。而通过遗传算法(GA)和增量逆传播学习算法(IBP)对其权值和阈值进行优化、将其参数进行改进，可以有效降低其不确定性，使其网络输出趋于稳定。因此，本文采用BP神经网络(BP)、遗传算法优化的BP神经网络(GA-BP)和增量逆传播学习算法优化的BP神经网络(IBP-BP)对蓄水坑灌冬季果园土壤温度进行预测，以期为蓄水坑灌冬季果园管理的工作提供理论支持。

1 材料与方法

1.1 试验区概况

本试验区位于山西省太谷县果树所，试验进行时间为2015年11月28日-2016年3月15日和2016年11月28日-2017年3月15日，共计217 d。试验区海拔将近800 m，属暖温带大陆性气候，年平均气温为5～10 ℃。试验采用苹果树品种为红富士矮砧苹果树。

1.2 试验设计及项目测定

本试验主要进行蓄水坑灌条件下冬季土壤温度的动态变化监测研究，以蓄水坑为中心，在相邻两蓄水坑中心连线上距坑壁5、15、25、35 cm处沿垂向每隔10 cm埋设一个温度探头，最大埋设深度80 cm，共32个测点。并在地表距坑壁25 cm处布置一个温度探头，用于监测地表温度。土壤温度监测点布置如图1所示。

图1 温度监测点布置图

试验测定的项目包括蓄水坑内的大气温度、地表温度和各土层土壤的温度。地表温度和各土层土壤温度采用HZR-8T型温度自动测量仪进行测定，数据采集频率为30 min/次，仪器测定精度为0.1 ℃。蓄水坑内的大气温度数据采用Adcon Ws无线自动气象监测站监测的气象资料，数据监测频率为15 min/次。

1.3 数据处理及模型评价

采用Microsoft Office 2013软件对试验测得的原始数据进行整理，并通过MATLAB 2016分别对BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T神经网络模型进行训练和验证。对模型预测性能的评价指标采用平均相对误差MAPE和均方根误差RMSE，计算公式如下：

(1)

(2)

式中:Zy为各神经网络的预测值;Zs为实测值;N为样本数量。

2 模型构建

2.1 BP神经网络模型

BP神经网络是目前应用颇为广泛的一种分层网络，其结构包括输入层、隐含层和输出层[10]。BP神经网络采用的学习过程包括输入层的前向传播以及误差的反向传播，在一定的规则下，样本值由输入层经过隐含层到达输出层如此正向传播，若输出结果未达到预期目标输出值则开始反向传播，将误差信号按原来的方向返回，从输出层依次经各隐含层直至输入层，过程中通过梯度下降法不断修正权值和阈值，不断减小期望输出与实际输出的误差，直到神经网络误差小于给定值时停止训练。

由此可见，BP模型的建立主要是确定输入、输出和隐含层，并通过恰当的优化算法求出权值和阈值。本研究采用地表平均温度、蓄水坑坑内平均温度、沿相邻两蓄水坑中心连线距坑壁的距离和距离蓄水坑壁5 cm处土壤的各土层(8层)最低温度作为模型的输入项，输出项为距蓄水坑坑壁15、25和35 cm处土壤的各土层最低温度。

隐含层节点数目的大小直接影响网络的误差以及训练时间的长短，因此，在模型的建立中准确选择隐含层的节点数目尤其重要。由上文可知BP-WSPI-T神经网络模型输入层和输出层的节点数分别是11和8，将其代入经验公式[11]，可计算出隐含层节点数的大致范围，再结合试算法进行确定，经过大量的试算，最后将模型的隐含层节点数定为14。因此，模型最优的拓扑结构为11-14-8，如图2所示。

图2 BP-WSPI-T神经网络模型结构

(3)

式中：x为模型隐含层节点数；i和j分别为模型的输入和输出层神经元数目；m为经验值，取1～10之间的整数。

试验共测定217 d，每天测得一组数据，共测得217组数据，每组含8个数据。把测得的数据样本按照8∶2的比例随机分为训练组和预测组，则训练组174组数据，预测组43组数据。

2.2 遗传算法优化的BP神经网络模型

在传统的BP神经网络模型中，基于梯度下降法的训练函数，虽然收敛速度快，但求得结果对初始值的依赖比较大，如果初始值取值不恰当，非常容易收敛于局部最小值。

遗传算法最早在1962年被提出，是一种基于自然选择和自然遗传的发展过程而建立的数学模型，是一种随机搜索算法[12]。遗传算法是对样本中的个体一一编码，计算其适应度，然后将个体排序并进行一系列操作(选择、交叉和变异)，从而使获得的下一代具有更好地适应环境的能力。随着遗传算法的不断运行，样本一代代优化，越来越逼近最优解。由此可见，遗传算法的优化结果不依赖参数初值，具有一定的全局优化能力。因此，本文将采用遗传算法对BP模型的权值和阈值进行优化，以期提高模型的预测精度。

通过遗传算法优化权阈值的步骤如下：①将随机赋予神经网络的初始权阈值编码，得到新的种群；②计算种群个体的适应度即实际输出与预测输出误差绝对值之和的倒数，并通过适应度函数值判断权阈值的好坏；③选择最大的适应度函数值所对应的权阈值，遗传给下一代；④进行交叉、变异，获得新的种群；⑤重复第二步到第四步的3个步骤，过程中神经网络的权阈值不断优化，直到训练目标达到要求，将种群解码，获得最优的权阈值，其步骤如图3所示。参数值的设定：交叉概率为0.3，变异概率为0.1，学习速率为0.05，动量因子为0.8，训练精度设为0.001，训练次数设为10 000。

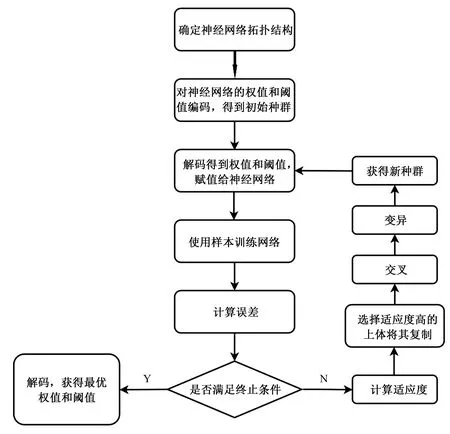
图3 遗传算法优化的BP神经网络流程图

2.3 增量逆传播学习优化算法的BP神经网络模型

IBP网络模型是在BP神经网络模型的基础上，根据增量学习规划在有效区间内对神经网络的权值进行调整，得到的一个优化模型[13]。IBP模型的参数设定：学习率为0.6，动量常数为0.8，其他参数和BP神经网络模型的参数相同。具体数学方法和权值调整区间见下式：

Δωab(k)=s(k)λδb(k)Oa(k)

(4)

(5)

式中：Δωab(k)为节点a和b之间的连接权值；s(k)为比例因子；λ为学习速率；δb(k)为节点b的误差梯度；Oa(k)为节点a的激活水平；n为运行实例的迭代次数；B(p)实例权值的取值范围。

3 结果分析

3.1 训练组结果分析

为比较BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T 3个模型的预测效果，对训练组的实测数据和预测数据之间的一致性进行分析，其线性关系如图4所示。由图4可知，距坑壁15 cm处训练组样本的BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T模型拟合成的直线的斜率分别是0.995、0.998和0.997，拟合度R2分别是0.997、0.998和0.995；距坑壁25 cm处训练组样本的BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T模型拟合成的直线的斜率分别是1.004、1.003和0.998，拟合度R2分别是0.998、0.999和0.998；距坑壁35 cm处训练组样本的BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T模型拟合成的直线的斜率分别是1.003、0.999和0.998，拟合度R2分别是0.998、0.999和0.997。由此可见，3个模型对训练组样本土壤温度的预测效果都比较好，在距离坑壁15、25和35 cm处，GA-WSPI-T模型的预测结果相对最好，斜率最接近1，IBP-WSPI-T模型次之，BP-WSPI-T模型的预测结果相对较差。

图4 训练组样本实测值与预测值的线性拟合

为进一步明确模型的计算精度，对3个模型的平均相对误差(MAPE)和均方根误差(RMSE)进行统计学分析，并通过t检验对训练组实测数据与预测数据的差异性进行分析，其统计学分析结果如表1所示。由表1可知，3个模型的平均相对误差大小(MAPE)表现为GA-WSPI-T

表1 训练组实测值与预测值统计学分析结果

3.2 预测组结果分析

通过训练组174组数据对模型的优化训练，BP-WSPI-T模型、GA-WSPI-T模型和IBP-WSPI-T模型均得到最优的权值和阈值。分别将预测组43组数据代入训练好的3个模型，得到预测组的土壤温度预测值。为比较BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T 3个模型的预测效果，对预测组的实测数据和预测数据之间的一致性进行分析，其线性关系如图5所示。由图5可知，距坑壁15 cm处预测组样本的BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T模型拟合成的直线的斜率分别是1.019、1.003和1.015，拟合度R2分别是0.994、0.998和0.985；距坑壁25 cm处预测组样本的BP-WSPI-T、GA-WSPI-T和IBP-WSPI-T模型拟合成的直线的斜率分别是0.994、0.997和0.994，拟合度R2分别是0.996、0.998和0.995；距坑壁35 cm处预测组样本的BP-WSPI-T、BP-WSPI-T和IBP-WSPI-T模型拟合成的直线的斜率分别是0.995、0.997和0.995，拟合度R2分别是0.997、0.998和0.995。由此可见，3个模型对预测组样本土壤温度的预测效果都比较好，在距离坑壁15、25和35 cm处，GA-WSPI-T模型的预测结果均是最好，斜率最接近1，IBP-WSPI-T模型次之，BP-WSPI-T模型的预测结果最差。

为进一步明确模型的计算精度，对3个模型的平均相对误差(MAPE)和均方根误差(RMSE)进行统计学分析，并通过t检验对预测组实测数据与预测数据的差异性进行分析，其统计学分析结果如表2所示。由表2可知，3个模型的平均相对误差大小(MAPE)表现为GA-WSPI-T

图5 预测组样本实测值与预测值的线性拟合

表2 预测组实测值与预测值统计学分析结果

4 结 语

本文采用传统BP神经网络模型、遗传算法优化的BP神经网络模型和增量逆传播学习算法优化的BP神经网络模型对蓄水坑灌冬季果园土壤温度进行预测。结果表明，与传统的BP神经网络相比，通过遗传算法优化的BP神经网络和增量逆传播学习算法优化的BP神经网络对蓄水坑灌冬季果园土壤温度的预测准确率更高，稳定性更高，收敛速度也相对更快。其中，遗传算法优化的BP神经网络模型预测效果最好，避免了传统BP神经网络的一些缺陷，平均相对误差达到4.4%，可以用来对冬季果园土壤温度进行预测。