钝体逆向喷流减阻降温数值模拟*
王立强,钱勤建
(中国空空导弹研究院, 河南洛阳 471009)
0 引言
高速飞行的飞行器在飞行过程中头部会受到明显的气动加热,因此准确的气动热估算和合适的热防护方法设计尤为重要。
热防护方法有许多种,如采用多层隔热结构[1]、金属热防护[2-4]、安装机械整流锥[5]及注气热防护,其中注气热防护中比较典型的方式是反向喷流[6]。相对于其他热防护方法,反向喷流设计简单且能有效降低驻点附近的气动加热。通过喷射气流阻挡自由来流直接冲击头部形成复杂的干扰流场:包括弓形激波、马赫盘、回流区、桶激波、再附激波等现象,由于弓形激波被推离飞行器头部一定距离,使得头部驻点附近的气动加热得到降低[6]。因此研究将弓形激波有效推离头部是降低头部气动加热的关键所在。
文中采用基于SST湍流模型的N-S方程数值模拟方法,计算并系统分析了质量流量、喷口面积对钝体减阻、降温的影响,并对相关机理进行深入分析。
1 数值方法及验证
1.1 数值方法
文中控制方程采用基于SST湍流模型的N-S方程,在笛卡尔坐标系中,方程的守恒形式为:
(1)
式中:Q为守恒变量;F、G、H为无粘通量;FV、GV、HV为粘性通量。
计算外形采用圆形钝头体(简称钝体),直径50 mm,圆形喷口位于来流正前方,直径默认为4 mm。计算网格见图1。网格采用全结构网格。网格节点数为157(轴向)×151(径向)。
边界条件入口采用inflow-outflow, 出口采用outlet, 对称边界为symmetry。
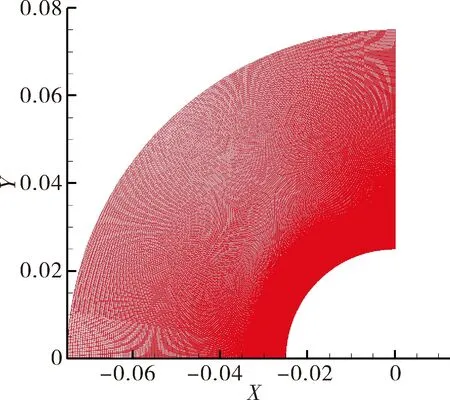
图1 计算网格
1.2 验证计算
计算工况条件如下:
自由来流:马赫数3.98,总压1.37 MPa,总温397 K。
喷流:马赫数1.0,总温300 K。
喷流与自由来流总压分别为P0j、P,其比值定义为总压比,以PR表示,即为了叙述方便,对一些表达式进行了简化,如PR=0.4以PR0.4表示,其他情况以此类推。
流场的密度分布CFD数值计算结果与试验结果[7]比较见图2,由图中可以看出流场中的激波结构比较复杂:逆向喷流在与来流相遇之前先形成一个马赫盘,与来流相遇形成一道强弓形激波,在再附回流区附近还存在再压缩激波等。数值方法都很好的模拟出这些流场特征,而且不同总压比情况下的马赫盘位置与试验结果非常吻合,激波位置一致性良好。

图2 CFD与试验密度曲线对比
图4给出了文中计算与文献[8]计算结果(以Ref表示)的压力曲线对比(其中横轴表示自水平轴线沿钝体壁面的角度,称为周向角,示意图见图3所示),图5给出了计算与文献[7]试验结果(以Exp表示)的压力曲线对比,可以看出文中计算的压力、热流值与文献中的结果吻合良好。

图3 周向角示意图

图4 压力曲线对比
热流曲线中纵轴以斯坦顿数表示热流无量纲值。

图5 壁面热流曲线对比
综上所述,文中计算结果合理准确,说明计算方法是正确的,网格生成是合理的。
2 计算结果与分析
分别从质量流量、总压比、喷口马赫数、喷口面积角度对钝体绕流流场特性及钝体减阻降温进行分析。
2.1 质量流量
固定喷口面积、喷流马赫数、喷流总温,研究改变喷流质量流量对复杂干扰流场特性的影响。
本节通过调整总压比大小可以改变喷流质量流量。
表1、表2分别给出了仿真工况及质量流量值。

表1 仿真工况

表2 质量流量
图6给出了不同喷口压力下的温度场,在不同总压比的作用下,喷流干扰流场可能出现三种流动状态:长射流穿透状态(即LPM)、振荡状态、短射流穿透状态(即SPM)。本仿真条件下,产生长射流的总压比PR为0.15~0.28,产生振荡状态的总压比是PR=0.2,产生短射流总压比为PR≥0.4,分别见图6(a)、(b)、(c)。
长射流模态:其形成是由于喷流出口压力较小,喷口呈现过渡膨胀或充分膨胀状态,穿透能力强,钝体小角度附近的弓形激波被推的距离较远,弓形激波的头部更尖锐。从图6(d)左侧图能清晰地看到流场中由喷流形成了多个射流元。
振荡流模态:在某些条件下,喷流与弓形脱体激波相互作用,产生自激振荡导致流场不稳定,流场一直在做无规则扰动,喷流喷出的气体没有有效地覆盖钝体表面,从而使得斜激波后面的高温气体的热量不断传到钝体壁面,因此可能会导致钝体壁面的温度比无喷流状态下还要高[9],振荡流若干扰动过程见图6(b)。
短射流模态的形成是因为喷流出口压力较大,喷口呈现欠膨胀状态,喷口附近形成马赫盘且流动中仅包含一个射流元被主流弓形激波中止形成马赫盘(图6(d)右侧图),因此喷流与自由来流交界面上形成的激波距离钝体表面较近,此种模式下流场是稳定的。PR为0.4~12.0条件下的流场均为短射流模态。值得注意的是,短射流流场中的喷流穿透距离比长射流的距离要近,尽管其喷流总压比要大于长射流模态的压比。
表3给出了不同质量流量(总压比)情况下计算得到的钝体阻力系数。
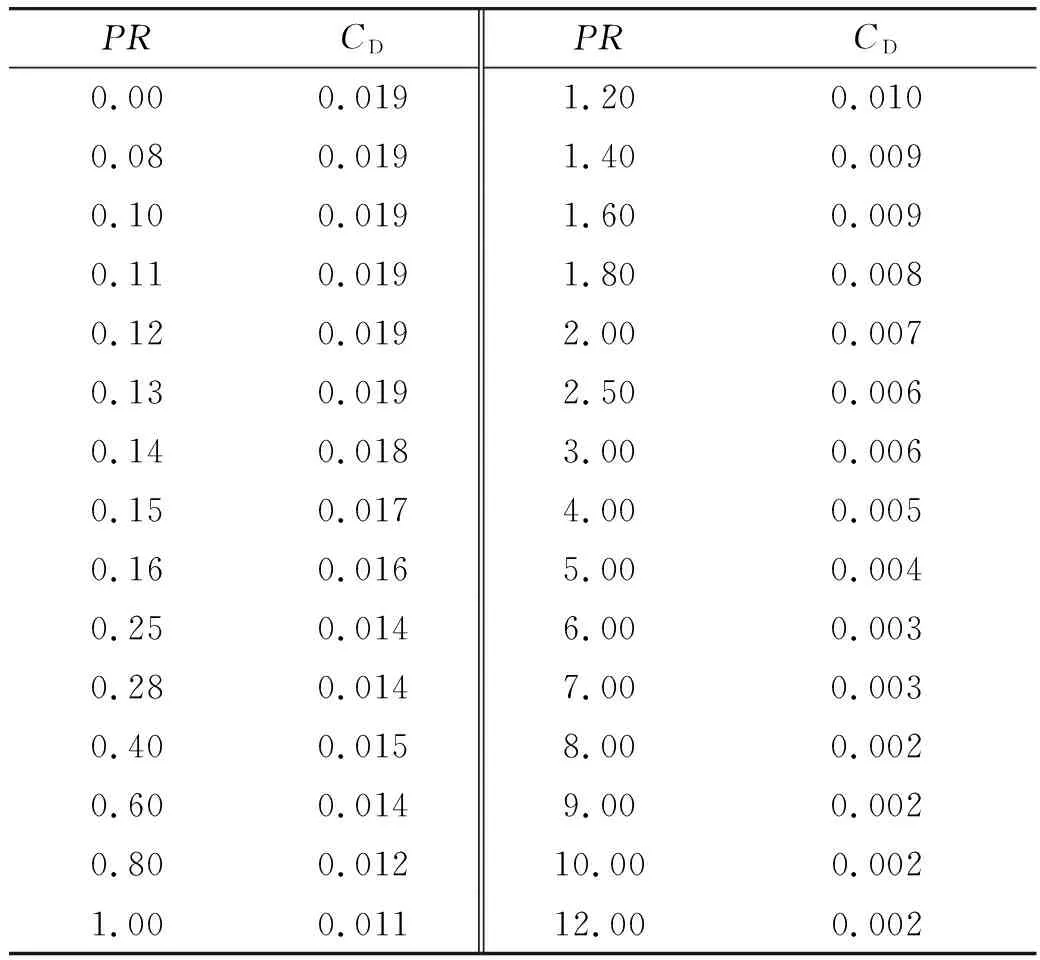
表3 阻力系数
阻力系数曲线见图7。横轴表示总压比,纵轴表示阻力系数。由该图可以直观看出,随着总压比增大,钝体阻力呈单调减小趋势,长射流(LPM)的阻力大于短射流阻力(SPM)。长射流与短射流之间的阻力系数存在一个跳跃的间断,这主要是总压比PR=0.2附近处存在不稳定流场模态导致。

图7 阻力系数
图8给出了质量流量变化时钝体表面压力分布曲线。由此图可以看出,在有喷流情况下,喷流质量流量越大则表面压力越小,短射流比长射流时的表面压力小。压力峰值基本出现在再附激波的再附点位置。此外,长穿透射流的峰值及下游表面压力比无喷流状态的压力还要大。

图8 表面压力曲线
钝体表面热流随总压比变化曲线由图9给出。从图中可以看出,钝体表面热流的分布特点与压力分布特点类似,此外,长射流的热流密度值明显比无喷流及短射流的热流密度值要大。

图9 表面热流曲线对比
2.2 喷口尺寸
固定喷流马赫数Maj、喷流总压P0j、喷流总温T0j。分析喷口直径d的变化对复杂干扰流场特性的影响。
喷口直径d分别为1 cm,4 cm,6 cm三种规格。
数值仿真工况见表4。

表4 仿真工况
数值仿真得到的温度场如图10所示,表面热流如图11所示。
从数值模拟结果可以看出,喷口直径越大防热效果越好,即喷口直径d=1.0 mm的防热效果最差,d=4.0 mm较好,d=6.0 mm最好,主要原因是喷流与激波作用后在钝体前部形成了回流区,回流区角度较小的区域受喷流气体影响,喷流气体温度较低,导致回流区域下方温度较低,而远离喷口区域的回流区受斜激波加热则温度较高。随着喷口尺寸增大,热流峰值位置所在的角度增大,d=1.0 mm时的热流密度的峰值位置在27.5°附近,d=4.0 mm时的热流密度的峰值位置在35°附近,d=6.0 mm时的热流密度的峰值位置在42.5°附近,峰值之后,热流下降比较明显,主要原因是喷口尺寸增大使得弓形激波和再附激波形成的包络外形变大,再附点位置与钝体表面距离增大及弓形激波与钝体表面距离增大有利于减弱气体对壁面的气动加热效果。
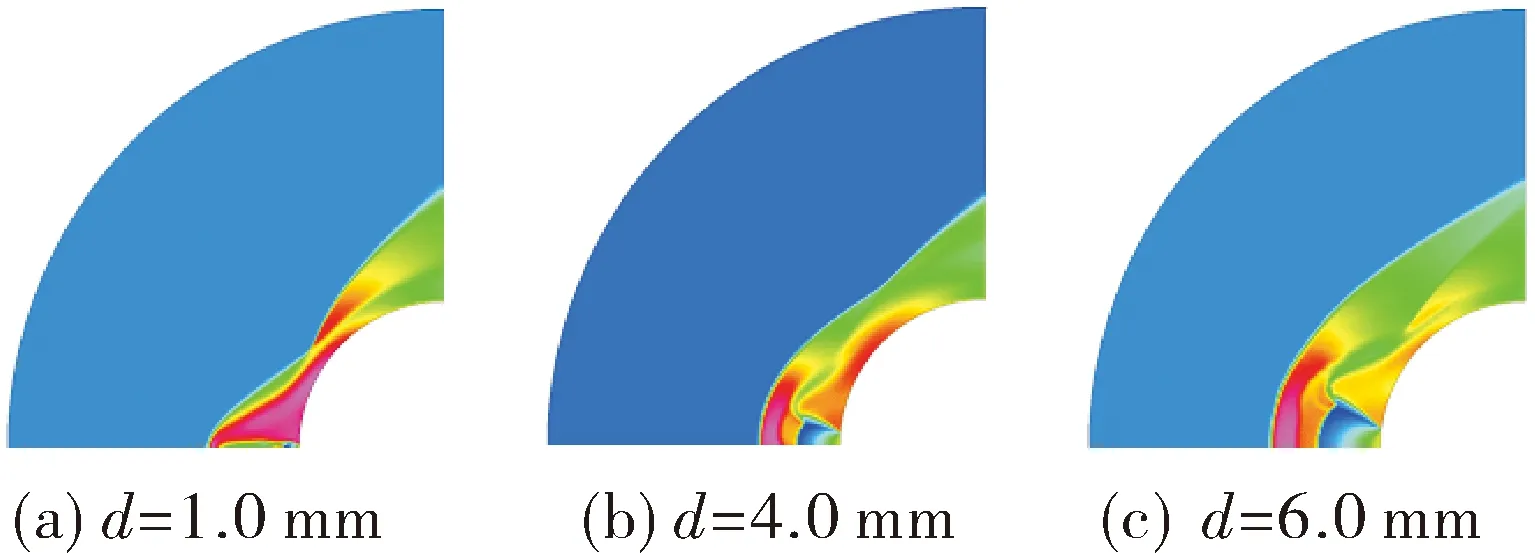
图10 不同喷口直径的温度场

图11 表面热流曲线对比
表5给出了不同喷口直径的阻力系数。

表5 阻力系数
由表中可看出,随着喷口面积增大,阻力系数减小,6 mm口径的阻力比1 mm阻力减小56.8%。
3 结论
文中通过对超声速钝体逆向喷流流场进行数值模拟,研究了质量流量与喷口尺寸对逆向喷流减阻、降温的影响,得出如下结论:
1)文中验证算例中,密度曲线、压力曲线及壁面热流曲线与文献[7]中的试验数据吻合良好,说明数值计算方法是准确的,网格生成是合理的。
2)在某特定流场工况下,喷流流场存在长射流穿透模态、振荡模态和短射流穿透模态。随着质量流量增大,钝体阻力呈逐渐减小趋势(中间可能存在跳跃间断,这是由于振荡模态导致的); 质量流量越大钝体表面热流越小。
3)固定质量流量等相关参数,在此流场工况下,喷口面积越大阻力越小,热流也越小,因此在钝体头部允许情况下可尽量扩大喷口面积以更好的减阻降温。
4)不论在何种工况下,壁面热流的变化基本上都是先增大后减小,最大值处主要是受再附激波影响,热流达到最大。

