基于多属性折中决策的空面制导弹药配置方案评价与优选*

王晓光，何晓夫，武学祺

(中国兵器工业集团公司航空弹药研究院， 哈尔滨 150036)

0 引言

空面制导弹药是指通过轰炸机、战斗机、无人机、飞行器等空中平台发射或投放，对敌方地面与地下目标进行有效、精确打击，以此减少己方伤亡，完成近距空中支援、纵深精确打击等作战任务的武器装备[1]，已经在现代战争中发挥了重要的作用[2-3]。随着科学技术的发展以及新时期作战任务的需求，新型空中平台迅速涌现，与其匹配的新型空面制导弹药成为各国研制的热点。而武器配置方案评价与优选是进行空面制导弹药详细设计的前提与基础，具有重要意义[4]。然而，在配置方案论证阶段的许多评价指标无法量化，如作战能力、效费比等指标值与权重存在大量不确定性；同时，评价指标之间又存在着一定的矛盾性和不可公度性，致使目前配置方案评价主要以定性分析为主。目前，针对空面制导弹药配置方案的评价与优选研究相对较少，尚未有一套科学合理的武器配置方案综合评价方法。基于此文中提出一种空面制导弹药配置方案综合评价方法，并进行实例分析，验证了评价方法的合理性与可行性。

1 基于多属性决策的评价原理

多属性综合评价是采用合适的评价方法对备选方案进行多因素多准则的分析和对比，并获得最优方案为决策人员提供参考意见。

设方案集为A={A1,A2,…,An}，指标集为C={C1,C2,…,Cm}，则多属性决策问题可由以下n×m决策矩阵D来表示：

(1)

其中，yij为方案Ai在指标Cj上的评价值，i∈N,j∈M。

多属性决策问题主要涉及内容为：①决策矩阵的标准化；②评价指标的权重确定；③方案的综合排序。

1.1 决策矩阵的标准化

文中研究对象的属性类型主要为效益型，其属性集用T1表示，采用向量规范化法[5]对属性值进行标准化计算：

(2)

1.2 评价指标权重的确定

文中采用组合赋权法进行指标权重的确定，即采用群组层次分析(AHP)法[6]确定指标主观权重，熵权法[7]确定指标客观权重。

1)基于群组AHP法的主观赋权法

①邀请本领域相关方面的n个专家组成评价小组。

②确定评价指标体系及评价标准，构造比较判断矩阵T=(tij)n×n，其中tij表示因素i和因素j相对于准则Bk的重要程度，判断值参考1～9比率标度进行确定，因素j与i比较的判断值为tij=1/tij。

③计算单一准则下权重向量。

权重向量的计算就是求解上一步骤得到的判断矩阵T的最大特征值λmax对应的特征向量，即TW=λmaxW的特征向量W=(ω1，ω2，…，ωn)T。求解特征向量采用方根法，其计算如下：

(3)

其中特征值计算如下：

(4)

④一致性检验。

为了保证权重计算结果的合理性和可靠性，还需要对判断矩阵进行一致性检验。引入一致性比例CR=CI/RI来检验判断矩阵的一致性，其中CI=(λmax-n)/(n-1)为一致性指标，RI为平均随机一致性指标。当CR<0.1时，认为判断矩阵满足一致性要求。

⑤最终指标权重向量的确定。

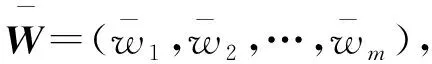
(5)

2)基于熵权法的客观赋权法

①将xij进行正向化处理，并计算第j个指标第i个方案所占的比重pij：

(6)

②计算第j个指标的熵值ej：

(7)

其中k≥0,ej≥0，k=1/log(m)。

③计算第j个指标的差异系数gj：

gj=1-ej

(8)

④计算第j个指标的熵值ωj：

(9)

3)组合赋权法

设主观赋权法获得的指标权重集为ω1j(j=1,2,…,n)，而客观赋权法获得的指标权重集为ω2j(j=1,2,…,n)，则最终的指标权重集由下式确定：

ωj=θω1j+(1-θ)ω2j

(10)

其中，θ为偏好系数，文中取θ为0.5。

1.3 基于多属性折中决策的综合评价方法

为了能够全面、具体、科学的论证空面制导弹药配置方案，文中采用VIKOR法对其进行评价与分析，计算过程如下[8]：

1)决策矩阵标准化

设有m个方案，n个属性，xij表示第i个方案在第j个属性下的评价值，则采用如1.1节所述的计算方式对决策矩阵的元素进行标准化。

(11)

(12)

3)计算各属性的权重值

采用如1.2节确定各个属性的权重值。

4)计算各个方案到理想解的距离

通过加权求和的方法求出最终的距离：

(13)

(14)

其中，Si为第i个方案到正理想解的加权距离，代表最大群效应；Ri为第i个方案到负理想解的加权距离，代表最小后悔值；ωj为第j个属性的权重。

5)计算VIKOR值

(15)

式中：Qi表示第i个备选方案的VIKOR值，其中S*=minSi，S-=maxSi，R*=minRi，R-=maxRi，ν是最大群效应权重，取值0～1。

6)方案排序

基于上述步骤计算得到的Qi值，对所有方案进行排序，Qi值最大的为优选方案。

2 评价与优选流程

基于多属性折中决策的综合评价流程如下：①构建评价指标体系；②构建方案集；③确定决策矩阵与指标权重；④对方案集进行评价；⑤确定排序与优选方案。

3 实例简介

为使某新型飞行平台具备对地作战能力，需研制相匹配的航空制导弹药。在经费有限的条件下，只能优选出一种重量级弹药先进行研发，但首先研制何种重量级的弹药最能满足平台需求，何种重量级弹药对地作战效果最好等这些问题是需要由论证确定。文中以此问题为实例进行分析。

4 评价结果与验证

1)指标体系构建

为了综合客观对比不同重量级航空制导弹药的作战效果，经过专家多次讨论最终确定选取评估指标为：隐身能力C1、飞行能力C2、打击能力C3、效费比C4、平台适应性C5。

2)构建方案集

基于某型飞行平台挂装约束构建4种弹药配置方案：1枚重型航空制导弹药(A1)、2枚中型航空制导弹药(A2)、4枚轻型航空制导弹药(A3)、8枚超轻型航空制导弹药(A4)。其中，假设同一飞行平台在相同投放条件下不同重量级弹药的射程、打击精度相同。

3)指标主观权重计算

邀请航空制导弹药研究领域的5位专家对AHP法构造的判断矩阵进行对比打分，然后通过式(4)和式(6)对权重进行计算，其中比较判断矩阵T结果如下所示：

计算得到的评估指标C1～C5的主观权重分别为：0.104、0.2、0.396、0.086、0.214，即C3>C5>C2>C1>C4。

4)配置方案评分

对配置方案进行评价时采用1～5打分制，分值越高表明该项指标表现越好。为了综合客观的考虑其作战任务的特点，地面目标与地下目标的评分权重取为0.5。具体评分结果如表1所示。

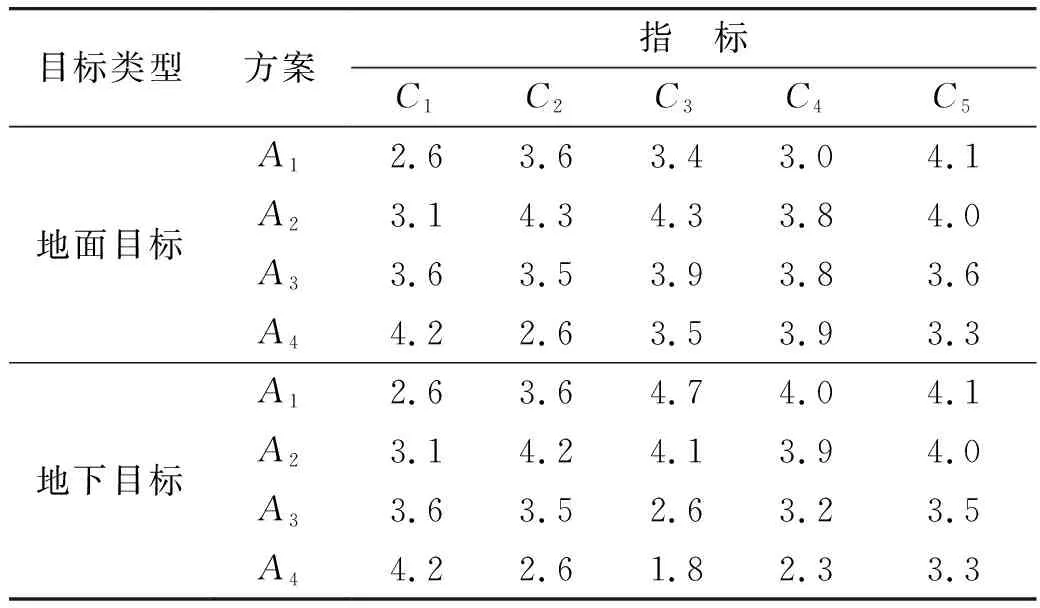
表1 评分决策矩阵

然后，采用组合赋权法对各个指标权重进行计算，结果如表2所示，指标权重排序为：C3>C2>C1>C5>C4，这表明打击能力、飞行能力对配置方案最为关键，其他3个方面可在后续详细方案设计中进行优化改进。

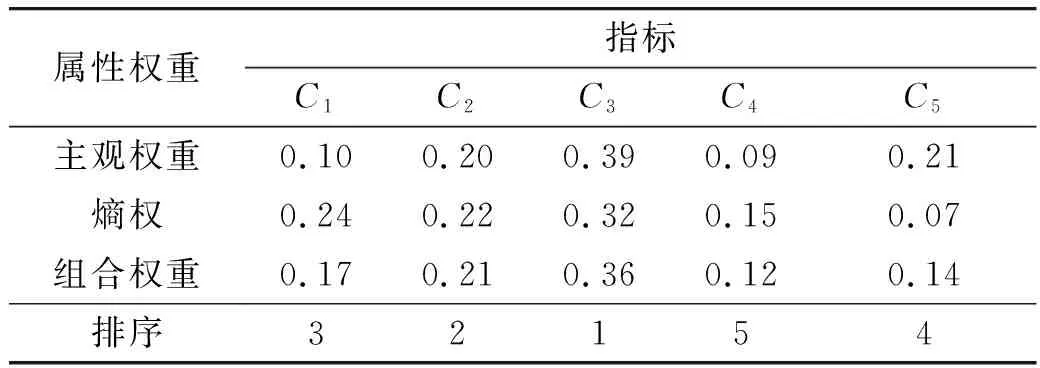
表2 基于组合赋权法获得的属性权重

5)方案评价、优选与验证

根据1.3节步骤计算得到VIKOR值如表3所示。

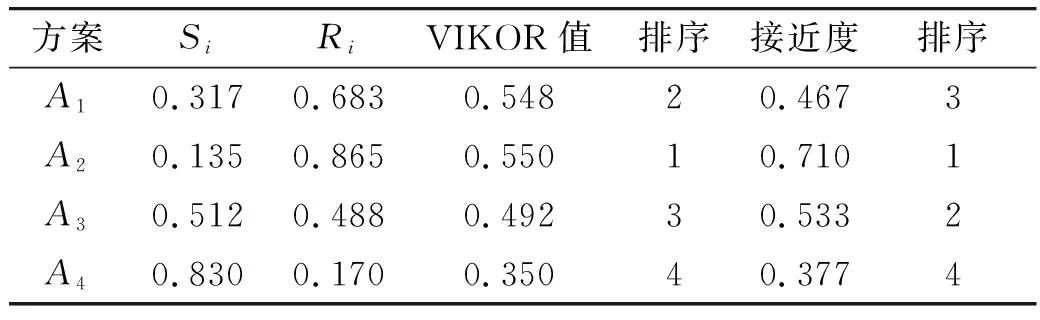
表3 综合评价结果

从表3中计算结果可知，航空制导弹药配置方案的综合排序为：A2>A1>A3>A4。为验证文中方法对方案优选和排序的合理性和可信性，采用TOPSIS方法[8]进行验证，计算得到的配置方案排序：A2>A3>A1>A4。综上可知这两种方法的优选结果相同均为A2方案，最差为A4方案，中间排序不同是由于这两种算法本身的差异造成的，主要原因在于：①TOPSIS法是通过计算备选方案到正负理想点的距离来进行最终决策，但VIKOR法既考虑了群体的意愿，又考虑了个体的意愿并进行折中；②TOPSIS法在计算距离时就引入了权重，而VIKOR法在计算正、负理想解的加权距离时才开始使用权重，减小了权重对评价算法的干扰，增强了最终计算结果的准确性。

5 结论

文中提出了一种基于多属性折中决策的空面制导弹药配置方案综合评价方法，且引入了组群AHP法和熵权法的组合赋权法来确定指标权重，这既能考虑专家的主观经验，又能考虑方案决策自身数据的客观规律，并以某新型飞行平台挂载不同重量级航空制导弹药的配置方案评价为实例，建立了相应的评价指标体系，得到了配置方案的评价结果，且与理想点法(TOPSIS)的评价结果相吻合，验证了其合理性与可行性。