动基座近程主动防护系统目标跟踪算法*

孙金雯，陈 曦，杜忠华，陆 谦，许国杰

(南京理工大学机械工程学院， 南京 210094)

0 引言

近程主动防护系统是一种作用在装甲车辆上的末端防御武器系统，一般由探测模块、控制模块和拦截模块组成[1]。探测模块负责来袭目标探测，获得其距离、速度与方位信息；控制模块负责目标跟踪解算与预测航迹，并提供最佳拦截参数，控制拦截模块动作；拦截模块负责正面迎击来袭目标使其毁伤，从而保护装甲车辆安全[2]。由于近程主动防护系统作用距离很近，其目标跟踪解算时间极短(约几百毫秒)，因此在目标交会拦截时，一般假设装甲车辆静止[3-5]，而探测系统固连于车身，也即忽略了量测坐标系位置变化。但实际装甲车辆运行时速为55～70 km/h，尤其轮式装甲车速度可达100 km/h，在系统跟踪解算时间内，车辆在水平面运行位移近乎装甲车辆车身长度，该水平位移及地面起伏导致的垂直位移对系统目标跟踪及火控解算精度影响很大。为了提高近程主动防护系统拦截精度，需研究车辆运动导致的雷达量测坐标系变化，即动基座下的目标跟踪算法。

无迹卡尔曼滤波(unscented Kalman filtering即UKF)无需计算雅克比矩阵，精度高，稳定性好，对强非线性系统能避免滤波发散，是一种常用的非线性雷达目标跟踪算法[6-7]。但一般雷达目标跟踪算法只考虑位置信息，由于近程主动防护系统中采用连续波雷达，测速精度高，因此，基于UKF算法引入径向速度量测(UKFR算法)，以提高目标跟踪精度[8]。在此基础上，提出基于比例采样的带径向速度量测的UKF算法(SUKFR算法)，采用比例对称采样策略(scale symmetry sampling)，进一步改善滤波效果，提高目标跟踪性能。

文中通过坐标变换进行雷达量测空间配准，建立来袭目标运动模型，进行SUKFR目标跟踪解算。通过Matlab Monte-Carlo仿真，对比UKF、UKFR、SUKFR三种算法跟踪效果，验证了SUKFR算法能显著提高目标跟踪精度与收敛性。

1 雷达量测空间配准

目标跟踪算法要求对目标的多次量测处于同一量测坐标系下[9]，以建立目标运动模型，进行跟踪解算。但装甲车辆的运动会导致雷达量测坐标系也随之变化，因此需结合车辆的运动状态，进行雷达量测空间配准。

1.1 车体坐标系oxcyczc

以车体质心为坐标原点，取车体纵轴车头方向为xc轴正向，垂直于车身对称平面并指向车身右侧方向为yc轴正向，zc轴由右手法则确定，朝向车身上方为正，如图1所示。该坐标系为非惯性坐标系，随装甲车辆的移动而移动。

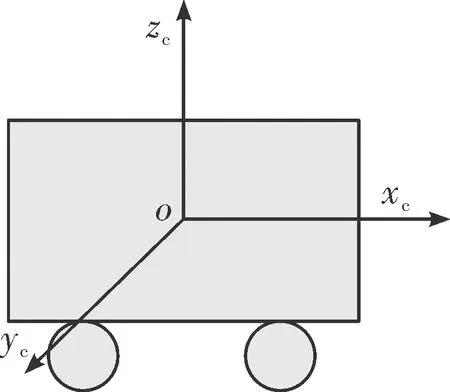
图1 车体坐标系

1.2 雷达量测坐标系oxryrzr

雷达量测是基于雷达量测坐标系，对于近程主动防护系统，雷达固连于装甲车辆车身，因此雷达所测目标运动参数即目标相对车体的运动参数，可认为车体坐标系与雷达量测坐标系一致(或有一个由安装位置决定的转换矩阵)。由于本系统配备的探测雷达位于车辆中心，探测范围为车身360°，因此认为车体坐标系与雷达量测坐标系近似一致。

雷达量测信息通常基于极坐标系，而目标运动模型一般基于直角坐标系，导致目标跟踪的非线性，因此文中采用精度较高的UKF非线性滤波算法。雷达量测信息由极坐标系转换至直角坐标系公式为：

(1)

其中(r,α,β)为雷达量测的径向距离、俯仰角和方位角;(xr,yr,zr)为来袭目标在雷达直角坐标系中位置坐标。

1.3 初始坐标系oxyz

装甲车辆配备GPS与惯导系统，可实时提供可靠的车辆位置、姿态与速度信息。设雷达刚探测到来袭目标瞬间车体坐标系的绝对位置为初始坐标系，该坐标系位置固定，不随车辆运动而改变。由于雷达坐标系的位置与姿态角随车辆运动而变化，此时需将在运动的雷达坐标系下探测到的目标运动参数转换至固定的初始坐标系下，便于解算分析，如图2所示。

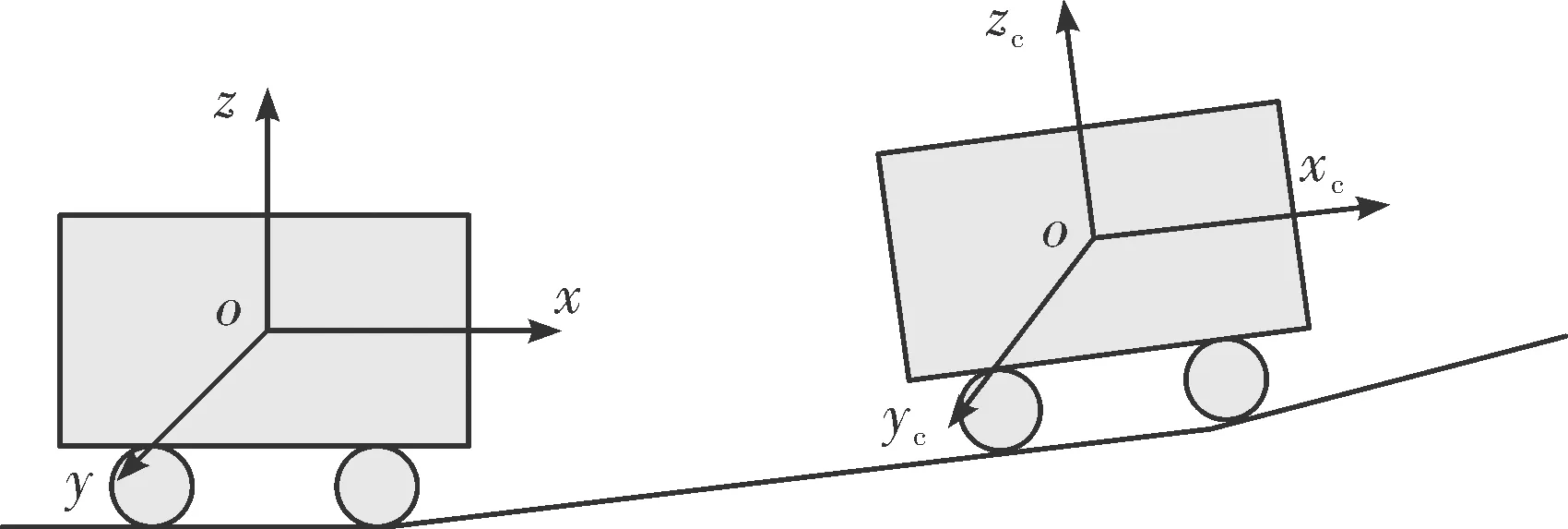
图2 初始坐标系

1.4 量测信息空间配准

假设当前雷达探测数据为(r,α,β)，转换到雷达直角坐标系下为(xr,yr,zr)，车辆当前车体坐标系相对于初始坐标系的位置差为(Δx,Δy,Δz)，欧拉角差为(Δψ,Δθ,Δφ) 。其中ψ为偏航角，即车体坐标系xc轴在水平面投影与初始坐标系x轴间夹角；θ为俯仰角，即车体坐标系xc轴与水平面夹角；φ为横滚角，即车体坐标系zc轴与通过xc轴的铅垂面间夹角。如图3所示。

图3 坐标系欧拉角

可得旋转变换矩阵为：

因此，装甲车辆运动时雷达量测参数转换至初始坐标系下为：

(2)

经过上述坐标转换，动基座下雷达量测参数均处于同一坐标系，可进行目标跟踪解算并预测来袭目标飞行轨迹。

2 目标跟踪算法

2.1 运动方程

近程主动防护系统为末端防御武器系统，工作时来袭弹已飞至弹道末端，工作过程极短，可认为该时间内来袭目标弹体姿态不变，弹道固定，近似匀速直线运动，弹丸推力不规则或外界气流等较小运动状态干扰可视为量测噪声处理。因此文中选用三维CV模型来描述目标运动状态。笛卡尔坐标系下，来袭目标离散状态方程为：

(3)

式中：σ2为可调节参数；T0为雷达采样周期。

2.2 量测方程

常规三坐标雷达只测量距离、方位角与俯仰角[10]，本系统探测雷达还可提供精确的速度信息。雷达径向速度量测也会随着雷达坐标系的运动而产生偏差，不过偏差较小，可视为径向速度量测误差处理。

雷达量测基于极坐标系，量测参数有径向距离 、俯仰角 、方位角和径向速度。文中假定来袭目标位置与速度信息噪声为独立高斯白噪声，因此速度与位置量测误差统计独立。雷达量测方程如下：

Zk=h(Xk)+Vk

(4)

2.3 SUKFR算法

一般雷达量测信息均有随机误差，直接使用量测信息解算拦截参数会导致较大误差。因此需对雷达量测信息滤波处理，以提高拦截精度。UKF算法基于线性Kalman滤波，使用无迹变换处理非线性传递的均值与协方差，通过选取特定样本逼近状态后验概率密度，没有忽略高阶项[11]，因此滤波精度高，稳定性好。

传统UKF算法不能自适应调整Sigma点与原均值点间距离，该距离会随状态向量维数增大而增大，从而导致非局部采样现象[12]，尤其对强非线性函数，会导致滤波精度降低。由于本系统状态向量维数较高，量测方程非线性较强，因此考虑基于UKFR算法采用比例对称采样策略[12]对原Sigma点集采样点间距进行比例修正，以消除“非局部效应”，提高目标跟踪性能，即SUKFR算法，其基本计算步骤如下：

1)计算Sigma采样点集及其权值

采样点:

(5)

(6)

式中:下标m表示均值，c表示协方差；参数λ=α2(n+κ)-n为缩放比例参数，用以降低预测误差；参数α决定采样点散布状态，取值范围为0.000 1～1；参数κ为冗余值，常取0；参数β为权系数，与状态量先验分布有关，取值非负；n为状态向量维数。

2)比例修正原Sigma点集得到新点集S

X(i)(k|k)=X(0)+a(X(i)-X(0)),i=0～2n

(7)

其中，a为比例参数，取值范围为0～1。

3)计算新S点集的一步预测

X(i)(k+1|k)=AX(i)(k|k)

(8)

4)计算状态量一步预测及协方差矩阵

(9)

(10)

5)根据一步预测，再次使用UT变换，产生新Sigma的点集

(11)

6)计算新Sigma点集的预测观测量

(12)

7)加权求和得系统预测均值与协方差

(13)

(14)

(15)

8)计算Kalman增益矩阵

K(k+1)=PXkZkPZkZk-1

(16)

9)计算系统状态更新和协方差更新

(17)

(18)

3 仿真与分析

3.1 仿真条件设置

使用Matlab对SUKFR算法进行50次Monte-Carlo仿真，以检验SUKFR算法跟踪性能，并与UKF、UKFR算法进行对比分析。

设来袭弹进入雷达探测范围时初始距离70 m，俯仰角20°，方位角30°，速度-260 m/s；初始协方差阵P=1 000 eye(6)；过程噪声调节参数σ2=1；雷达量测距离、俯仰角、方位角与速度标准差为σr=0.1 m、σα=5.5 mrad、σβ=5.5 mrad、σr=0.3 m/s；采样周期T=0.001 s；观测时间0.23 s；无迹变换参数α=0.01，β=2，κ=0，状态向量维数n=6，比例修正参数a=0.1。

3.2 仿真结果分析

Monte-Carlo仿真结果如图4～图6及表1，表2所示。

图4 目标运动航迹

图5 位置均方根误差

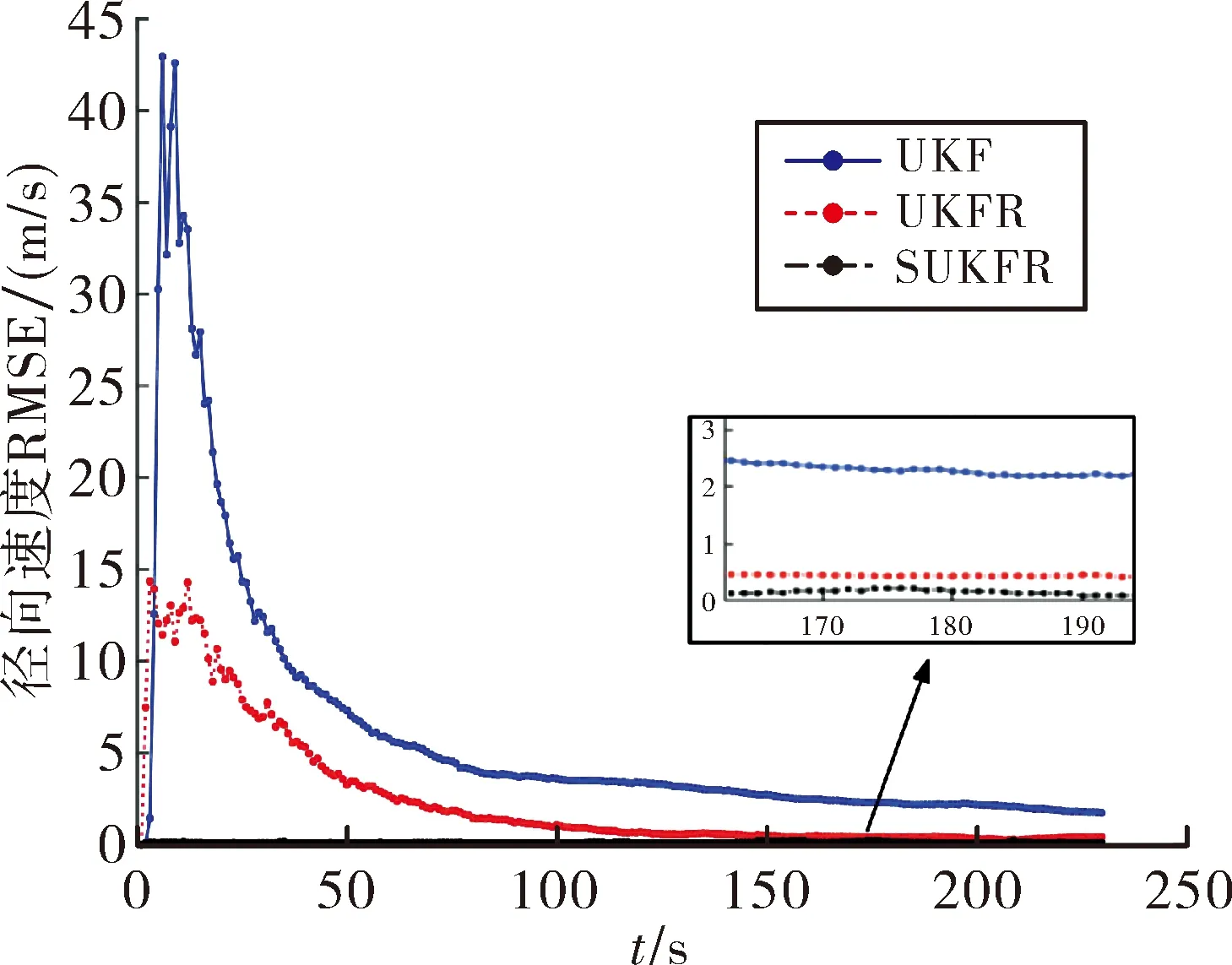
图6 速度均方根误差

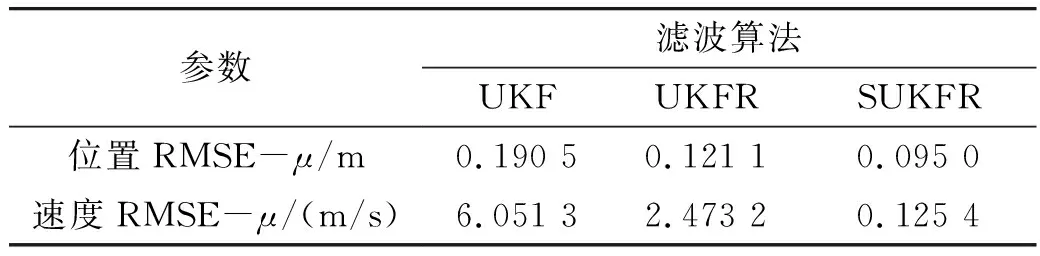
参数滤波算法UKFUKFRSUKFR位置RMSE-μ/m0.190 50.121 10.095 0速度RMSE-μ/(m/s)6.051 32.473 20.125 4

表2 50次Monte-Carlo仿真RMSE均方差值

文中采用均方根误差(RMSE)为目标跟踪算法评价准则，通过RMSE曲线收敛程度与RMSE均值、协方差等参数判断滤波算法性能。

由图4可见，3种算法均能较好抑制量测噪声，使预测轨迹逼近真实轨迹，说明UKF算法精度较高，适用于本系统。

由图5，对于距离RMSE，3种算法收敛速度均较快，且收敛后误差均较小。其中，SUKFR算法初始误差远小于UKF与UKFR算法，且精度也较高。因此可见雷达径向速度量测的引入与比例对称采样策略的采用使得来袭目标位置参数目标跟踪效果有所改善。

由图6，对于速度RMSE，UKF算法由于不包含径向速度量测信息，无法及时修正所估计的径向速度，导致速度预测误差较大，收敛也较慢。UKFR算法较UKF算法径向速度预测的收敛速度与精度大大提高，可见径向速度量测数据的引入能显著改善速度参数滤波性能。而SUKFR算法较UKFR算法的收敛性与精度又大幅提升，可得对于误差较大的速度滤波，比例对称采样策略的引入可较好的消除UKF算法采样“非局部效应”，显著改善目标跟踪算法性能。

表1与表2通过50次Monte-Carlo仿真运算得到距离与速度的RMSE均值与均方差值，更直接的展示了图4到图6得出的结论。SUKFR算法较其余两种算法位置与速度参数的误差均值与均方差值均有所减小，表明SUKFR目标跟踪算法收敛最快、误差最小、精度最高，引入径向速度量测信息与采用比例对称采样策略提升了目标跟踪性能，特别是速度参数的预测精度。

4 结论

文中针对装甲车辆近程主动防护系统的目标跟踪关键技术，研究了车辆运动对其影响，并通过建立相应坐标系，对雷达量测进行坐标转换至同一坐标系，以修正车辆运动的影响。而后进行目标跟踪解算，基于UKF算法引入径向速度量测信息与比例对称采样策略以优化目标跟踪算法性能。通过Monte-Carlo仿真，对比了3种目标跟踪算法的跟踪效果，验证了文中所提出的两种优化策略能够改善目标跟踪算法的精度、收敛性与稳定性，尤其对误差较大的径向速度量测参数，滤波精度显著提升，可见对于近程主动防护系统，SUKFR目标跟踪算法能满足其性能需求。