基于极化敏感阵列的空频域导航抗干扰方法*
杨美娟,李 肖,郑 娇,吴 梦,杨 琨,袁渊明
(1 山东航天电子技术研究所西安分部, 西安 710119; 2 西安交通大学电子与信息工程学院, 西安 710049)
0 引言
随着北斗卫星导航系统的日趋成熟,其在军事、民用的各个领域应用越来越广泛[1]。鉴于电磁环境的日益复杂,特别是军事对抗强度的增大,卫星导航亟需抗干扰技术以弥补其脆弱性[2]。
目前导航信号抗干扰技术的研究侧重于普通标量天线,主要方法包括时域滤波、频域滤波和空域滤波。然而普通标量天线仅考虑了信号的空域信息,对信号的极化特性不敏感,只能获取其中某一维分量。相比前者,由完备电磁矢量传感器组成的极化敏感阵列可以获取至少两维电磁分量,在其基础上增加通道数,提高阵列天线自由度。此外,极化阵列可以利用干扰信号与期望信号在空域和极化域的特征差异,实现空间-极化联合域抑制干扰、增强信号[3-4]。
联合极化域的抗干扰技术大多围绕空域算法展开[5-7]。为进一步提高算法性能,常常将多种抗干扰技术组合使用,如极化空域联合抗干扰算法、极化空时抗干扰算法[8]。为便于工程实现,采用计算量较小的空频自适应算法达到同样的抗干扰性能。
因此,文中将极化阵列和空频自适应抗干扰算法相结合,研究如何在阵列孔径不变的前提下,发挥二者优势,提高抗干扰自由度,在抑制干扰的同时保持期望信号的增益。
1 极化敏感阵列信号模型
假设空间中P个远场信号入射到N元极化敏感阵列,则接收信号模型可以表示为:
x(t)=As(t)+n(t)
(1)
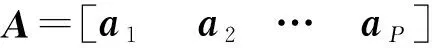
极化敏感阵列的联合导向矢量为:
ai=asi⊗api
(2)
其中:⊗表示Kronecker积;asi为空域导向矢量;api为极化域导向矢量。
(3)
(4)
这里,λ表示载波波长;(xn,yn)分别表示第n个极化敏感阵元的空间位置坐标;(θi,φi)分别表示第i个信号的俯仰角和方位角,俯仰角定义为信号来向与z轴的夹角,方位角定义为信号来向在xoy面的投影与x轴的夹角;(γi,ηi)分别表示第i个信号的极化辅助角和极化相位角,极化辅助角描述了y方向电场幅度与x方向电场幅度的比值,极化相位角描述了y方向电场和x方向电场的相位差。从式(4)可以看出,极化域导向矢量不仅与信号的极化域参数有关,也耦合了信号的空域参数。
为简化起见,选取双正交电偶极子为天线阵元,分别接收Ex和Ey电场分量,所有阵元在空间上按一定规律放置,如均匀线阵、均匀圆阵、矩形阵等。那么,极化域导向矢量简化为水平和垂直两个通道的电场信号,即
2 极化-空频算法简介
在利用极化敏感阵列的基础上,为了进一步提高抗干扰算法性能,文中提出了一种联合极化域的空频域导航抗干扰方法,以下简称“极化-空频算法”。该算法能够有效提高阵列自由度,抑制多个功率较强的压制式干扰。
算法基本思想是,将极化敏感阵列接收信号通过傅里叶变换分解成若干个频带,然后在每个频带上进行空域自适应滤波抗干扰处理。具体实现流程如图1所示。

图1 算法流程图
设天线阵列由N个双正交极化阵元构成,则通道数为2N,按照图1所示流程,对各通道接收的M个数据进行M点的离散傅里叶变换,将信号分割成M个频带,令第n个通道第m个频带的值为Xn(m),则第m个频带进行空域抗干扰处理的输入数据为:
(5)
为了使协方差矩阵的估计值更准确,采用多段数据协方差矩阵求平均值的方法,获取其最大似然无偏估计。令该通道从第1到第M时刻所接收的输入信号为第一个数据块,则第n个通道的第l个数据块为:
(6)
设第n个通道用第l个数据块做FFT后得到的第m个频带的值为Xn(m,l),则此时第m个频带值的输入数据可以表示为:
(7)
若共有L个数据块,则协方差矩阵的估计值为:
(8)
再结合空域抗干扰方法,这里选取经典的功率倒置算法,该算法无需导航信号的先验知识。权值计算公式为:
(9)

对各个频带的协方差矩阵分别求逆,代入式(9)求权值,即可得到极化-空频域算法的抗干扰权值。
算法具体步骤如下:
1)按照式(7)求第l段数据第m个频带值X(m,l);
4)将逆矩阵代入式(9)中即可得到对应频带的极化-空频抗干扰权值wopt(fm)。
需要说明的是,对接收数据求FFT时,均为每个通道独立进行;空域抗干扰处理是针对每个频带独立进行的,最终得到的权值矢量在每个频带都各不相同。
3 仿真验证
以宽带干扰设置典型场景,通过仿真实验对比传统空频算法与极化-空频算法的抗干扰性能。
针对北斗B3频点信号,分别采用普通4元矩形阵和双正交4元矩形阵,阵元间距均为半波长,采样频率为62 MHz。固定导航信号和干扰信号的极化方式均为右旋圆极化,干扰带宽覆盖导航信号带宽。
3.1 单个宽带干扰的抑制情况
设置干扰方位角为135°,俯仰角为84°,干噪比为60 dB,频域每段数据为1 024点。
对比图2(a)和图2(b),两种阵列均可以对干扰达到抑制效果。普通标量阵列在干扰位置处形成的零陷区域较大,且出现一个伪零陷(图2(a));极化敏感阵列在干扰位置处形成一个较尖的零陷,深度为-78.34 dB(图2(b))。

图2 单干扰空域方向图
图3为固定干扰的空域参数后导航信号的极化域方向图,图4为固定导航信号的空域参数后干扰的极化域方向图。对比两图可以发现,导航信号在极化域损失很小,并未形成零陷(图3);而干扰在极化域形成较深零陷(图4),说明极化敏感阵列引入极化信息后,仍能在极化域对干扰形成零陷,而导航信号损失较小。在下面两个场景中,极化域方向图类似,故不再一一列出。

图3 信号极化域方向图

图4 干扰极化域方向图
3.2 三个宽带干扰的抑制情况
在单干扰基础上,增加2个宽带干扰,方位角分别为180°、225°,对应俯仰角均为84°,干噪比为50 dB。
对比图5(a)和图5(b),两种阵列在三干扰情况下均能够抑制干扰。普通标量阵列除了在干扰位置处形成的零陷外,在其余非干扰位置处也出现带状零陷(图5(a)),对于处在该区域的导航信号接收极为不利;极化敏感阵列在各个干扰位置处形成较深的零陷(图5(b))。

图5 三干扰空域方向图
3.3 六个宽带干扰的抑制情况
在三干扰基础上,增加3个宽带干扰,方位角分别为90°、0°、315°,对应俯仰角均为84°,干噪比为40 dB。
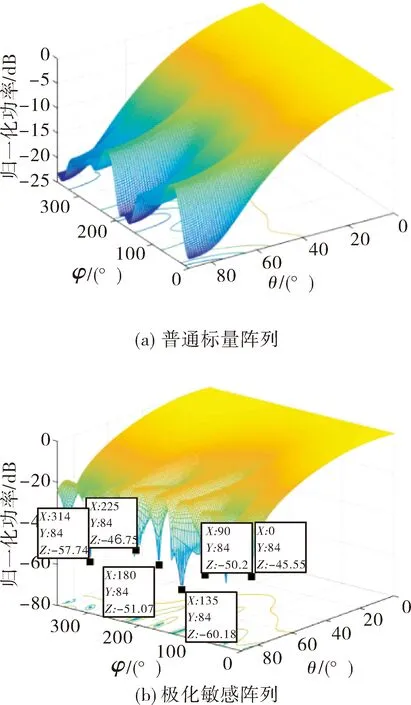
图6 六干扰空域方向图
从图6可以看出,在六干扰场景下,普通的空频域算法没有形成零陷,在干扰空间位置处出现较大区域的凹陷(图6(a));文中算法在各个干扰空间位置处均能够形成边缘陡峭的零陷(图6(b))。
综上,在多干扰场景下,采用普通标量阵列对非干扰区域影响较大,而采用极化敏感阵列均能在干扰位置处形成较深零陷,且保证期望信号增益损失较小。
4 结论
针对卫星导航系统面临干扰愈加复杂且多样化的现状,单维域抗干扰算法难以满足性能需求,文中提出了一种基于极化敏感阵列的空频域导航抗干扰方法。该方法在阵列孔径不变的前提下,利用信号极化域信息,有效提高抗干扰自由度。仿真验证了方法的有效性与优势,对工程实现有一定的理论指导意义。

