基于正常域的无故障数据条件下轴承隐患监测

张 媛1,，杜艳平1，高振清1，秦 勇，魏秀琨

(1. 北京印刷学院 机电工程学院，北京 102600；2. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

滚动轴承作为各种复杂机电系统的核心部件，其服役状态的监测一直备受学界和工业领域重视。在实际应用场景下，滚动轴承的故障虽然多表现为突发，但是实际上，其服役性能的劣化却是渐变的[1-2]。目前广泛采用的温度检测等传统故障诊断手段通常只能在严重劣化甚至已有故障时才能有效[2]。作为故障率最高的核心关键部件，如果只能做到故障后的诊断处理而不进行实时隐患监测以及相应的预警预防，可能会造成整机瘫痪、机毁人亡等无法估量的严重后果，因此，对大型机电装备的滚动轴承服役状态进行实时监测，进而准确识别隐患状态，是保证系统整体安全、高效运行的必要条件，精确的隐患监测具有重大的理论和实际意义。

在隐患监测方面，很多学者已经开展了广泛、深入的研究，尤其是在轴承早期故障诊断方面已有丰富的研究成果[3-7]。Zhang等[3]提出采用混合差分进化和生物地理学优化的方法提高轴承故障诊断的适用性和精确性，通过与神经网络辨识方法的对比验证了方法性能。Jiang等[4]提出基于l0范数嵌入最小熵卷积的方法提高轴承早期故障的特征提取有效性，进而提高诊断准确率。Antonino-Daviu等[5]采用改进的传统电流特性判别方法进行电机轴承的早期故障诊断。Abdelkader等[6]改进了基于经验模式分解的信号消噪方法，并采用包络谱分析进行故障的早期检测和定位。Yu等[7]针对强背景噪声中的微弱故障信号，提出基于固有时间尺度分解的稀疏编码收缩方法进行微弱故障信号的描述，并通过微弱故障仿真实验进行了验证。

在滚动轴承早期故障诊断的研究中，有相当大一部分是在已有的故障和正常数据样本的基础上进行的，或者采用仿真方法搭建故障模型，以获取故障仿真数据来进行方法有效性验证。在实际应用环境和现场工况下，多数复杂机电系统发生故障的频率很小，故障数据样本的积累数量十分有限，甚至对于较新的或使用年限较短的设备，完全没有故障数据样本，这将导致上述很多研究成果无法适用。虽然可以通过破坏性试验和模拟仿真等手段收集故障状态样本，但是前者通常面临高昂的费用，可行性不强，而后者仿真出的样本数据常与真实情况有差别，导致实际应用时效果不佳。

鉴于以上情况，张媛[8]在进行安全域研究的基础上进一步延伸，针对实际现场工况，为了解决故障数据缺乏的问题，提出正常域估计(normal region estimation,NRE)方法，以期能够在仅有正常状态样本的情况下，对滚动轴承的运行状态进行实时监测和判断。本文中首先给出正常域的概念、内涵及其形式化描述，然后提出基于凸包快速生成的正常域边界估计方法，梳理基于正常域估计的隐患监测具体实施步骤，并通过滚动轴承实验数据进行实验并分析结果。

1 正常域理论

1.1 正常域的概念

为了更清晰地阐述正常域理论和方法，首先给出正常状态的定义。正常状态是指不存在可能导致非安全事件发生的隐患或故障的状态。基于此，给出正常域的如下描述。正常域是针对具体的研究对象(如滚动轴承)，在研究对象的运行状态相关变量空间内，包含且仅包含正常状态数据的特征点的区域。

直观来说，正常域由其边界确定，其边界可理解为能够包住所有正常运行状态点的最小的闭合几何形状，即：在二维安全相关变量空间内，正常域为能够包围所有正常状态点的最小闭合曲线；在三维安全相关变量空间内，正常域为能够包住所有正常状态点的最小闭合曲面；在更高维空间内，正常域则为能够包住所有正常状态点的最小超平面。图1所示为二维空间内的正常域，其中x1和x2分别为2个状态特征变量，其中能包围住所有正常状态点的最小闭合曲线即为正常域边界。

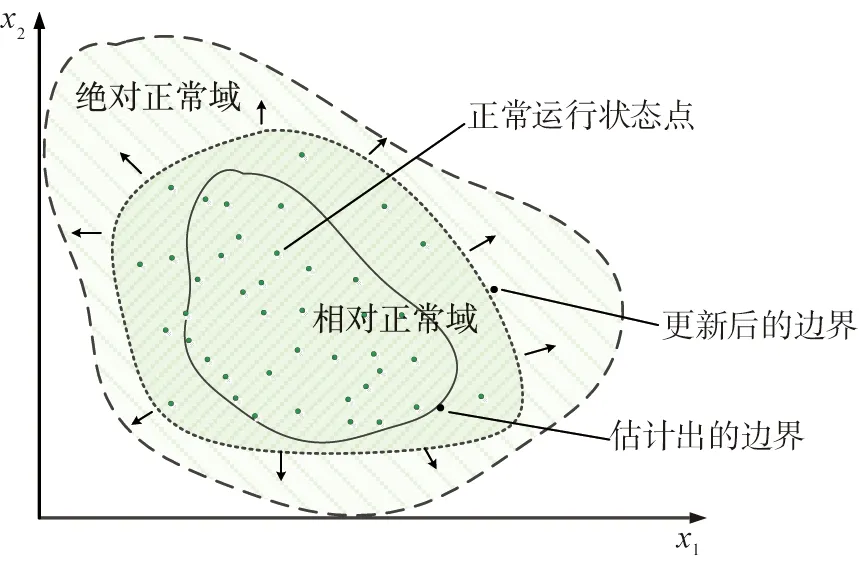
x1、x2—平面坐标下状态特征的第一、二维变量。图1 二维空间内的正常域

从理论上讲，正常运行状态点是无法被全部发现的，因此，本文中引申出绝对正常域的概念。在实际工程中，估计出的某时刻的未包含全部正常状态点的正常域边界称为相对正常域。相对正常域包含在绝对正常域内，从集合的角度来看，相对正常域是绝对正常域的子集，即在实际工程应用中，估计出的正常域边界均为相对正常域边界，而随着正常状态点的不断积累，相对正常域边界可不断更新，这可理解为相对正常域向绝对正常域的逼近。本文中所讨论的正常域边界均指相对正常域边界，简称正常域边界。

正常域边界的最主要功能是用于将状态空间划分为正常域和异常域(非正常域)，正常域边界可用分类决策函数描述为

f(X)=sign[g(X)]，

(1)

式中：X=(x1,x2,…,xn)∈n为运行状态相关变量空间中的状态特征向量，n为状态特征向量的维数；g(X)为划分2个不同区域的边界函数，即用于划分2个区域的边界方程可用g(X)=c来描述，c为常数。

1.2 基于正常域估计的隐患监测方法

针对具体的研究对象，从正常域估计的角度出发，完成其隐患监测需要2个步骤。

1)估计研究对象的正常域边界，确定运行状态正常域和异常域空间。主要包括采集研究对象的原始状态数据、原始数据的预处理、状态特征提取等必要的基础工作，然后基于所提取的正常状态特征点集，进行正常域边界的估计和更新。

2)基于正常域边界和安全裕度进行隐患监测。基于上一步中已经确定的正常域边界、正常域和异常域空间，首先由对象运行状态特征点所处位置，判断当前运行状态是否位于正常域内。如果位于正常域内，则计算当前状态特征点的安全裕度；如果当前状态处于异常域内，则立即给出报警信息。本文中将安全裕度定义为状态特征点到正常域边界的最小欧式距离，安全裕度越大，表明当前运行状态越不易发生异常。

简而言之，基于正常域估计的隐患监测方法的核心为正常域边界的估计，最终的定量化隐患监测结果依据安全裕度的计算给出。图2所示为基于正常域估计的隐患监测示例，其中状态特征变量有3个，即状态特征空间维数为3，正常域边界为超曲面。图中下方的状态特征点位于正常域内，通过计算该点到超曲面g(X)=c的最小欧式距离，可获得安全裕度[8]，从而给出定量化隐患监测结果。

需要说明的是，步骤1)可离线进行，待积累相对丰富的正常状态点并且正常域边界更新稳定后，再对其进行在线使用；步骤2)可在线实时进行。此外，随着正常状态数据的不断积累，在线使用过程中应注意定期进行更新，以保证隐患监测的准确性。

x1、x2、x3—状态特征的第一、二、三维变量；g(X)—正常域边界函数；c—常数。图2 基于正常域估计的隐患监测示例

2 基于快速凸包生成的边界估计方法

正常域边界的估计是进行隐患监测的核心和关键。凸包的概念与正常域的形式化描述有较大一致性，基于对正常域的直观理解，本文中提出利用求解能够包围某点集的最小凸包的方法进行正常域边界估计。

凸包问题是计算几何的基本问题之一，也是最基本和普遍的一种结构，在计算几何中占有重要地位。凸包是物体形状描述和特征抽取的重要工具，在故障诊断[9-10]、信息安全[11]、模式识别[12-13]、电力电子[14]等工程领域有广泛应用。

为了更形象地说明凸包与正常域的一致性，给出平面点集的凸包，如图3所示。平面点集的凸包是指包含平面点集内所有点，并且顶点属于平面点集的最小简单凸多边形，可形象地将其想象为一条刚好包围所有点的橡皮圈。

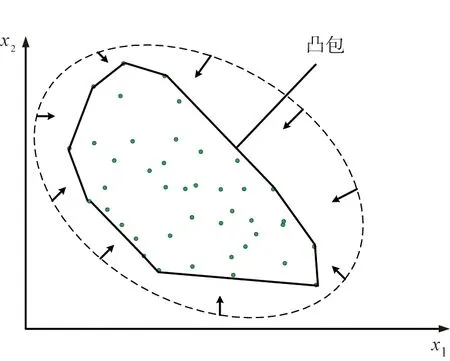
x1、x2—平面坐标下状态特征的第一、二维变量。图3 平面点集的凸包

凸包的计算方法有很多种，其中比较经典的有增量法、Graham扫描法、Jarvis步进法、分治法和快包法(Akl-Toussaint启发式方法)等。本文中综合考虑计算效率、速度和计算量，选用快包法进行凸包计算。

快包法首先选择最左、最右、最上、最下的点，这些点组成一个凸四边形(或三角形)，该四边形内的点必定不在凸包上，然后将其余点按最接近的边分成4个部分，重复进行。考虑到在大多数情况下，凸包仅由点集中的部分点构成，其余点则存在于凸包内部，快包法通过检测一些特殊点(如最远点)，不断产生不需要研究的区域，从而可以通过排除非凸包顶点、减少分析的点数来提高效率，因此，计算复杂度较低[15-16]。

3 实验与结果分析

为了验证正常域估计方法的有效性，采用文献[17]中的滚动轴承振动加速度数据实验，其数据采集实验台照片如图4所示。整套实验数据包含正常、滚动体故障、内圈故障、外圈故障4种轴承状态的振动数据，其中后3种故障状态的数据还分别包括不同故障程度时的数据。故障轴承包括SFK和NTN这2种品牌的轴承，轴承的各种故障均采用电火花加工，故障深度为0.279 4～1.270 mm，故障直径为0.177 8～0.533 4 mm。驱动电机采用功率为1.5 kW的Reliance品牌的电机，电机负载为0～2.25 kW (电机转速为1 797～1 720 r/min)。采用16通道数据采集设备，2种采样频率为12、48 kHz，采样时间10 s。

图4 轴承故障诊断实验台[17]

为了更严格地验证方法的有效性，选用故障直径最小、深度最小并且低转速、低采样频率情况下的3种故障状态数据与正常状态数据的结果进行对比，即本实验中所用的振动数据来自205-2RS JEM SKF型的深沟球轴承，故障直径为0.177 8 mm，故障深度为0.279 4 mm，电机转速约为1 730 r/min(约28.8 r/s)，采样频率为12 kHz。

在已有原始状态数据的基础上，按2节中所述，需要进行原始状态数据的预处理以提取有效状态特征。本实验中采用文献[8]中所提出的局部均值分解-能量矩的方法，提取能够灵敏表征状态变化的七维状态特征变量，具体可参见文献[8]中的第三章相关内容。由于七维数据无法直观展示，因此，取第一至三维数据进行图示。图5所示为正常和故障状态下的状态特征点分布情况。集中在图5(a)中最下方较集中的绿色数据点为正常状态数据，散布在其他区域的红色数据点为故障数据。可见，本文中选取的状态特征量能够较清晰地分离不同状态的数据。如图5(a)所示，正常状态特征点的分布相对比较集中，分布范围较小；而故障状态特征点的分布相对分散，分布范围也较大。该不同状态下的状态特征点分布情况也从侧面说明本文中提出的划分出仅包含正常状态特征点的正常域估计方法在进行隐患监测时可以有效区分正常和异常状态。同时，为了更清晰地展示本节中重点讨论的正常状态下数据点，从而为正常域曲面估计奠定基础，将图5(a)中下部的绿色数据点区域进行放大，结果如图5(b)所示，图中可明显观察到正常数据点的分布情况。

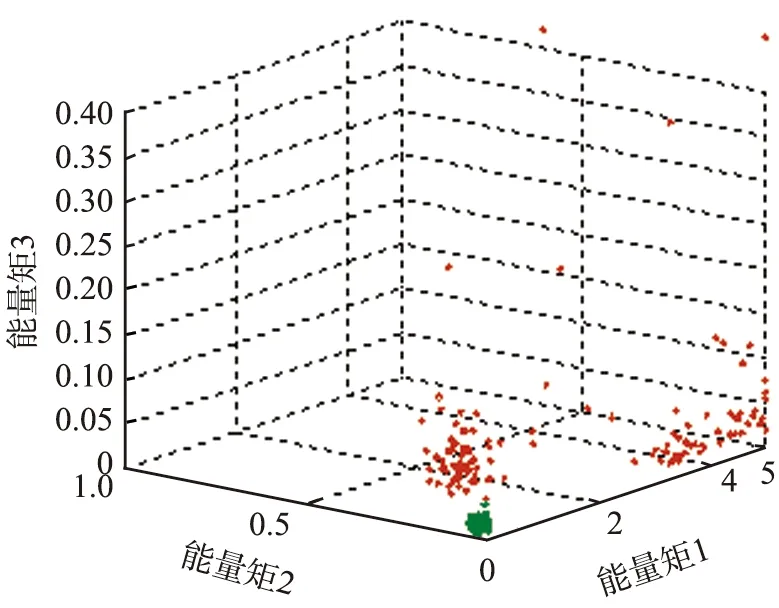
(a)正常和故障状态下的状态特征

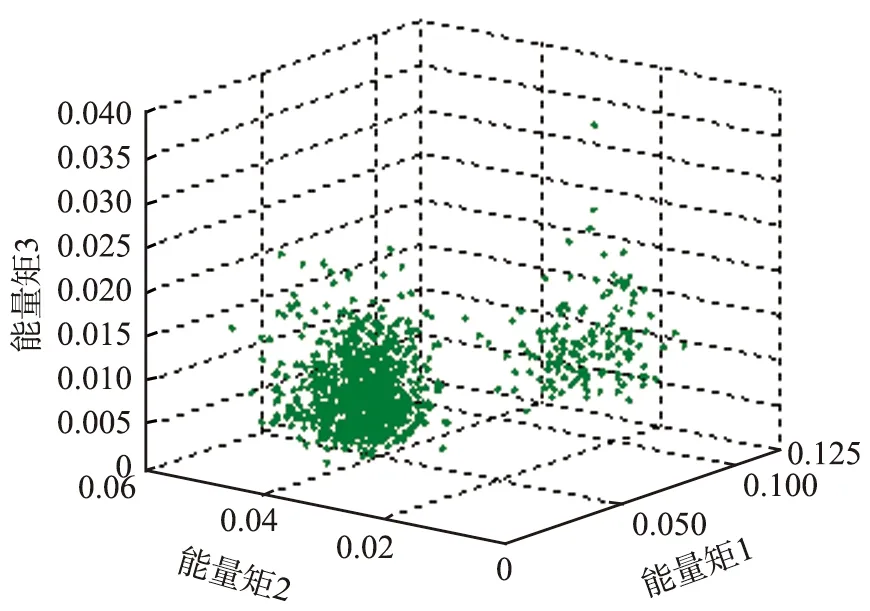
(b)正常状态下特征点的分布图5 正常状态下能量矩特征第一至三维数据点

在获取状态特征点后，采用快包法进行正常域边界估计。图6所示为由快包法生成的正常域曲面，该曲面能够将图5所示的所有正常状态数据点包含在曲面内部，并且曲面由多个三角形平面构成，这与快包法的计算原理相一致。同时，正是因为该正常域曲面的顶点均由正常状态数据点集中的数据点组成，所以该曲面可以有效地隔离故障状态数据点与正常状态。

图6 快包法生成的正常域边界曲面

为了直观展示图6中曲面在各维度上的形状，将该曲面分别向xy、yz、xz共3个二维坐标上进行投影，投影所得的各面上的二维闭合曲线如图7所示。其中绿色点为投影到二维平面上的正常状态能量矩特征，多段蓝色直线所构成的闭合曲线为投影到二维平面上的正常域边界。

为了考察快包法的计算效率，通过随机删减正常状态特征点集中个别数据的方法，统计多次使用快包法估计不同正常状态特征点集的正常域边界时的计算时间。在2.3 GHz主频CPU、8 GB内存的运算环境下，经过20次统计平均得到快包法的平均运行时间为0.016 3 s。

综上，快包法能够快速、有效地利用正常状态特征点完成正常域边界曲面的构造，能够划分正常域和异常域，并且计算很快，效率较高。

为了进一步验证正常域方法在进行轴承隐患监测时的可行性，在实验数据集中随机选取1组未用于正常域边界估计训练的正常状态数据，进行状态特征提取后在其中随机抽取1个能量矩状态特征点，坐标为(0.101 1,0.040 4,0.015 1)，如图8中的红色◎所示。观察该点与正常域边界曲面的相对位置可知，该点位于正常域边界曲面内部，被曲面所包含，可判定该点为正常状态点，与实际情况相符。判定完成后，按1.2节中所述进行该点的安全裕度计算。计算该点到凸包曲面上的最小欧式距离，可得该点到曲面上点(0.064 3,0.041 9,0.279 6)的欧式距离为最小，最小欧式距离为0.264 8，即该点的安全裕度为0.264 8。

由实验结果可知，虽然该方法计算效率高，有利于进行在线的实时更新和异常状态超快速识别，但是必须说明的是，该方法仅当正常状态和异常状态的状态特征分布区域的划分十分明显时，才能取得较高的辨识正确率，如本实验中的辨识准确率为100%，不存在将故障状态特征点包含在正常域曲面内的情况，但是当状态特征提取时对各状态的灵敏度不高时，采用该方法将会出现正常状态点与异常状态点的分布区域混叠的现象，此时所获得的正常域边界将会包含部分异常状态特征点，从而直接导致辨识准确率的下降。也正是因此，该方法所估计出的正常域边界大都偏保守，需要在使用过程中不断进行动态更新或积累足够丰富的正常状态数据，才能进一步扩大正常域范围，进而保证在实际工程应用时的误报率处于较低水平。

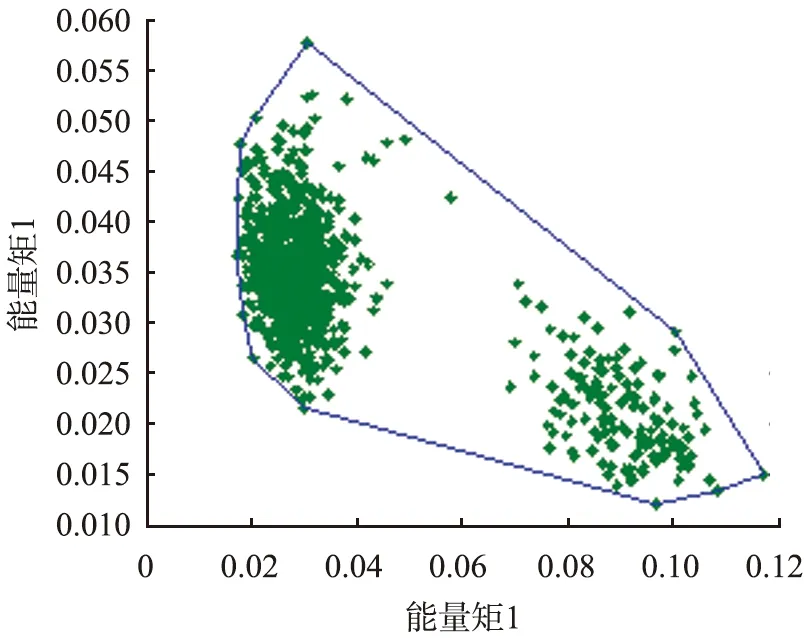
(a)xy投影面

(b)yz投影面

(c)xz投影面图7 基于快包法的正常域边界曲面投影

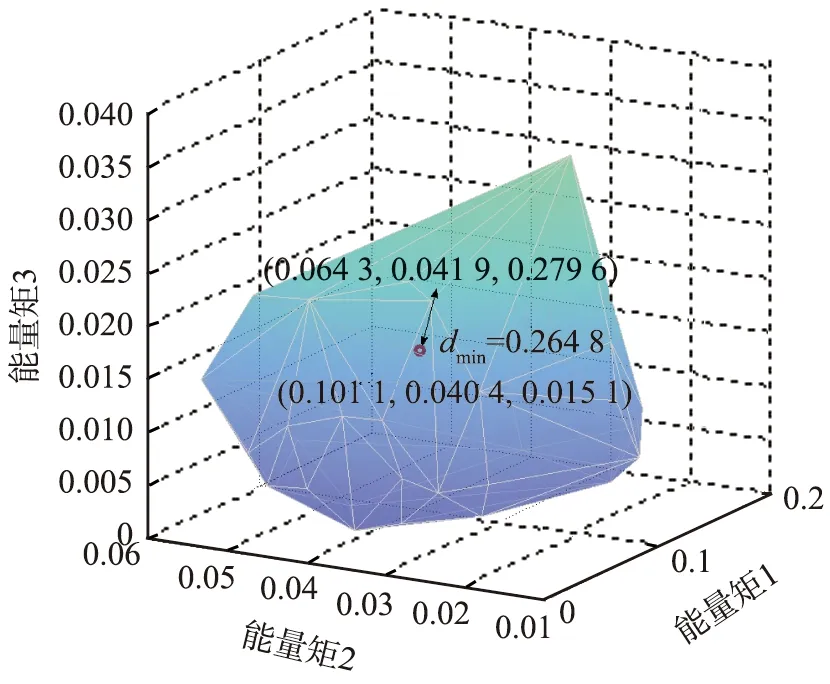
dmin—能量矩状态特征点(0.101 1,0.040 4,0.015 1)到凸包曲面上的最小欧式距离。图8 监测和安全裕度计算实例

4 结论

本文中针对实际工况下常出现的无故障数据情况，创新性地将正常域理论引入滚动轴承的隐患监测中，详细阐述了正常域的概念及其形式化表达，并分步骤给出了基于正常域估计的隐患监测实现方法。为了解决其中最关键的正常域边界估计问题，基于计算几何中的凸包理论，提出采用快包法估计正常域边界，并通过滚动轴承及其振动加速度数据进行了边界估计实验，结果表明，基于快包法的正常域估计方法高效并且可行，十分有利于边界的在线实时更新。

在后续研究中，将针对快包法生成的边界偏保守的问题进行改进，尝试在保证计算效率的同时增加边界弹性，提升其适应性。同时，也将针对边界更新策略展开研究。