四种地下结构抗震设计简化分析方法对比1

徐琨鹏 景立平 宾 佳

四种地下结构抗震设计简化分析方法对比1

徐琨鹏1）景立平1）宾 佳2）

1）中国地震局工程力学研究所，中国地震局地震工程与工程振动重点实验室，哈尔滨 150080 2）湖南工业大学，土木工程学院，湖南株洲 412000

在地下结构抗震设计简化分析方法中，强制反应位移法将土层变形施加在有限元模型侧边界模拟地震作用，反应加速度法将土层加速度施加到整个有限元模型上模拟地震作用，此外还有仅将土层加速度施加到土层模型上模拟地震作用的方法。上述方法均规避了反应位移法中关于弹簧刚度的取值问题，提高了计算效率。本文以1个双跨箱形结构为例，用动力时程分析的计算结果作为校核，分析了强制反应位移法、反应加速度法和仅将土层加速度施加到土体中的简化分析方法在不同侧边距条件下的计算精度，再结合常用的反应位移法，对比分析了4种简化分析方法的误差。分析结果表明：使用强制反应位移法时，侧边距取为1倍结构宽度导致的误差最小，反应加速度法和仅在土体施加加速度的简化方法对侧边距取值不敏感，反应位移法在角点造成的误差最大。

地下结构 拟静力 简化分析方法 侧边距 计算精度

引言

21世纪初以来，伴随着城市化进程的不断加快，城市中可以使用的空间越来越少，通过建设和开发地下空间工程来提高城市空间利用率已经成为世界性的发展趋势。地下工程包括地下综合管廊、地下停车场、轨道交通、地下污水处理厂、地下商业综合体等（钱七虎，2017），其对于解决城市化进程中出现的土地紧张、环境污染、交通拥堵和能源浪费等问题都发挥着积极作用（陈晓强等，2010）。然而，地下结构的地震安全性并没有引起人们的重视，以往学者们普遍认为地下结构完全被土体所包围，地震时地下结构比地面结构安全（陈国兴等，2016），因而地下结构的抗震设计并没有受到充分的重视，这也导致地下结构抗震研究一直停滞不前。在1995年日本阪神大地震中，地下结构发生了严重破坏（Iida等，1996），科研人员才开始真正重视地下结构的抗震问题。

一直以来，中国缺乏专门针对地下结构进行抗震设计的统一规范，各种规范中所考虑的方法与参数各不相同。早期，大部分地下结构抗震设计沿用地面结构的静力设计方法，比如《铁路工程抗震设计规范（GB 50111—2006）》（中华人民共和国建设部，2006），就是用地面结构抗震的思想进行地下结构设计，但地下结构在地震过程中受地基土约束，变形也受土体控制（林皋，1990a，1990b），在抗震原理上与地面结构大不相同（Hashash等，2001）。

美国和日本对地下结构抗震开展研究较早，基于结构变形受土体变形控制这一核心思想，率先提出了很多实用的关于地下结构抗震简化设计方法（权登州等，2015），包括自由场变形法（Wang，1993）、反应位移法（川岛一彦，1994）和柔度系数法（Penzien，2000）。其中以反应位移法推广度最高，但在反应位移法的使用过程中，地基弹簧系数直接决定了计算结果是否合理，弹簧系数的取值需要通过6次有限元计算才能获得，计算过程比较繁琐且不准确。在规避弹簧系数的取值问题上，国内外诸多学者提出了改进方法，如片山幾夫等（1985）提出了反应加速度法；Tateishi（2005）提出了强制反应位移法和改进方法；刘如山等（2007）提出了有限元反应应力法，即将一维土层剪应力沿竖向微分，再将其作为水平体荷载离散到有限元节点上；刘晶波等（2008，2013）提出了地下结构Pushover分析法和整体式反应位移法，前者借鉴地面结构Pushover方法，施加倒三角形荷载同时推动带结构的土体和自由场土体，通过自由场土体变形控制位移，后者直接在挖除结构的土-结构边界上施加位移，再把反力施加到带有结构的土体。这些简化分析方法为地下结构抗震研究提供了思路，但其适用性和精度还有待进一步检验。

本文以有限元软件ABAQUS为计算平台，以1个双跨箱形地下结构为算例，通过反应位移法、强制反应位移法、反应加速度法和仅在土体施加加速度4种方法进行对比计算，再以动力时程分析的结果为参考，分析4种简化分析方法所得弯矩、剪力和相对位移的计算精度，验证4种简化分析方法的适用性与准确性。

1 常用地下结构抗震分析方法

1.1 动力时程分析法

动力时程分析方法以有限元软件为计算平台，建立土-结构相互作用模型。其基本模型是将土分割为二维平面应变有限元，采用梁单元模拟地下结构并与土体连接，仅考虑由场地底部往上传播的剪切波，侧边界采用固定竖向、释放水平向的方式，底边界则固定竖向，再从模型的底部输入地震动，进而分析得到水平地震作用下土-地下结构的地震反应规律，计算模型如图1所示。动力时程分析法是采用逐步积分的方式求解地下结构在地震荷载作用下每一时刻的动力响应，能够较好地考虑材料的非线性、地震动频谱、持时和幅值情况。动力时程分析方法能够较准确地反应地下结构的地震反应，该方法常被作为其它简化分析方法的校核标准，然而其对土体动力本构关系要求较高，计算非线性问题耗时较长，求解难度较大，因而对使用人员的专业知识要求较高，同时还需要具备较好的计算平台，通常只被应用于重大工程项目的抗震分析中。国内地下建筑抗震设计规范《地下铁道建筑结构抗震设计规范（DG/TJ 08-2064-2009）》（同济大学，2009）和《城市轨道交通结构抗震设计规范（GB 50909—2014）》（中华人民共和国住房和城乡建设部，2014）都引入了动力时程分析法。

1.2 反应位移法

反应位移法采用梁-弹簧单元建模（不包含土体），其中梁单元模拟地下结构，弹簧单元（正向和切向）模拟结构和地基土之间的相互作用。首先，计算出结构顶、底板位置处所对应土层最大位移差，再把此时刻对应的位移差施加在弹簧远离结构的一端，同时在自由场计算中提取出该时刻对应的结构惯性力和地层剪应力，并直接施加在梁单元模型上，采用静力的方法计算结构响应，其模型见图2。反应位移法的计算结果依赖于地基弹簧刚度的取值，通过有限元计算弹簧刚度的方法也比较繁琐，且其取值是否合理也有待商榷。同样，《地下铁道建筑结构抗震设计规范（DG/TJ 08-2064-2009）》和《城市轨道交通结构抗震设计规范（GB 50909—2014）》都借鉴了反应位移法。

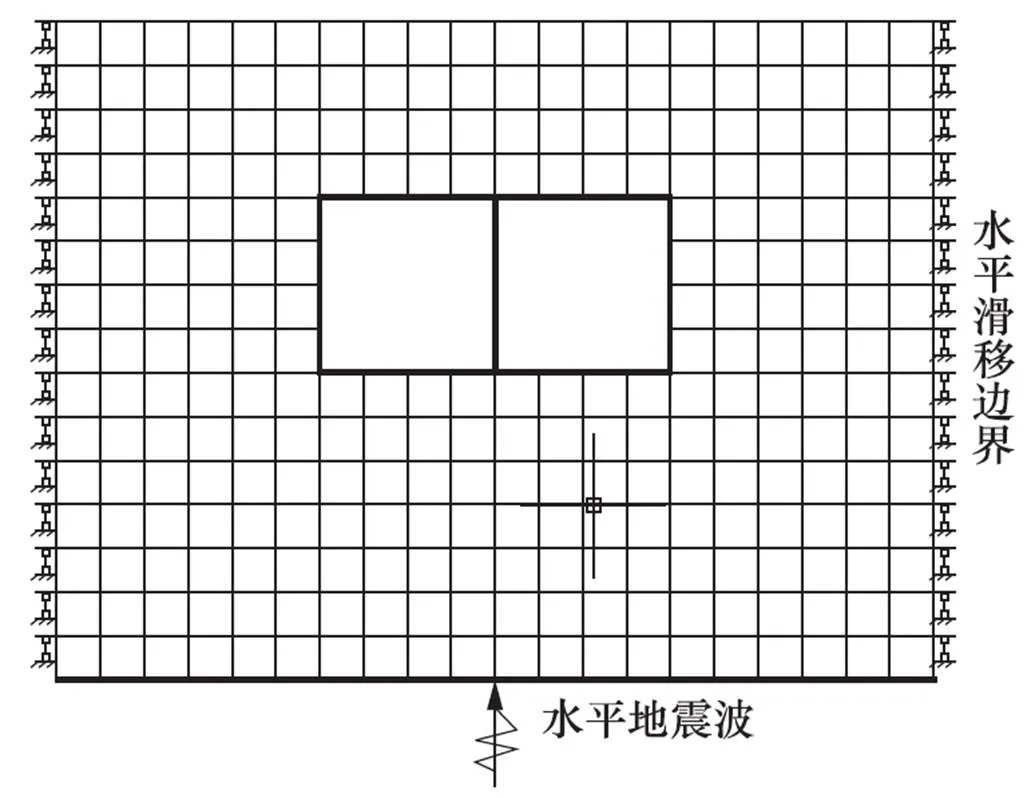
图1 动力时程分析法模型

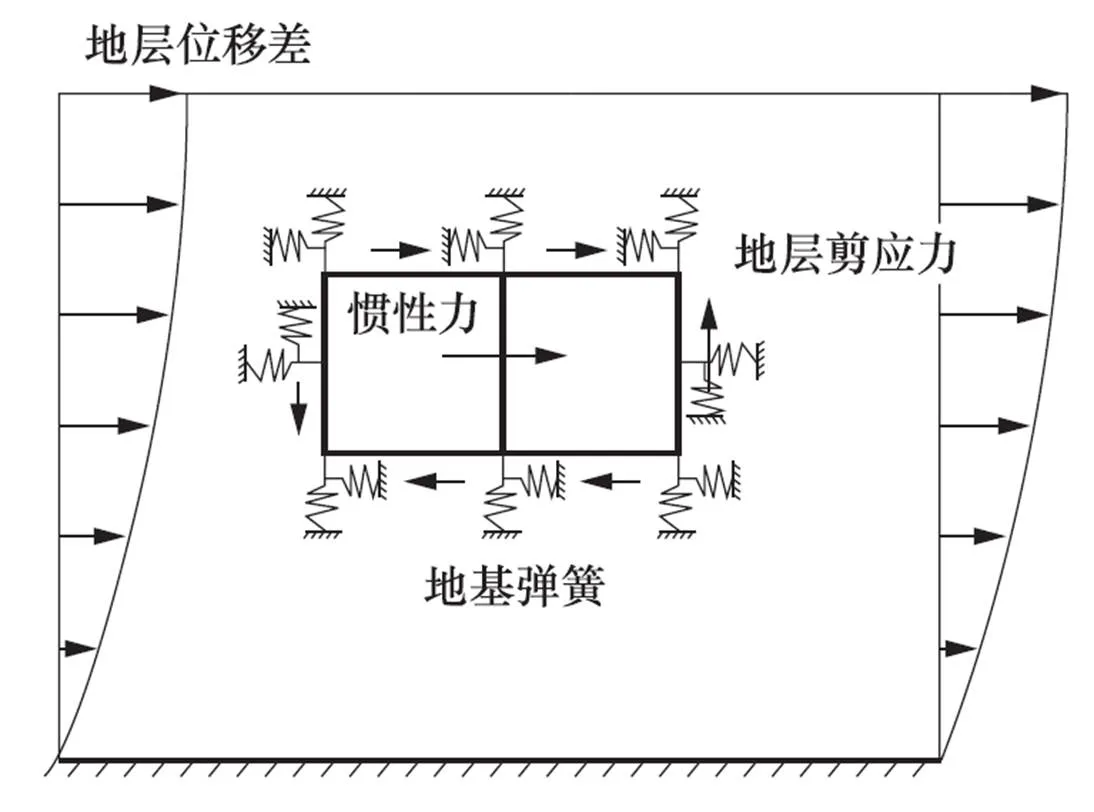
图2 反应位移法模型

1.3 强制反应位移法

土体边界施加强制变形是反应位移法的1种简化形式，进行简化主要是为了规避弹簧刚度的取值问题，计算过程和反应位移法相同。首先，需要通过自由场计算得到地震荷载下结构顶板和底板所处土层的最大位移差，此时结构变形最大，即处于极限响应状态，然后将该时刻自由场计算模型中全部土层的相对位移提取出来，并以强制位移的模式施加在有限元模型侧边界上，将动力问题简化为静力问题，从而得到结构响应，其计算模型如图3所示，其中为地下结构宽度，为地下结构到有限元模型侧边的距离。Tateishi（2005）指出，采用强制反应位移法处理动力作用虽然能够满足自由场应变在静力模型边界及附近准确传递，但远离模型边界处会因为土体阻尼的影响而发生衰减现象，尤以结构周围土层最为明显，应变值可衰减20%—50%。由于地下结构刚度通常大于土体刚度，因而结构变形比自由场变形小，如果选取的侧边距过小，土体阻尼作用将无法得到发挥，则相当于把自由场变形直接施加到了地下结构上，从而导致地下结构响应过大。由此可见，找到合适的侧边距是强制反应位移法准确求解结构响应的关键。

1.4 反应加速度法

反应位移法也可以通过反应加速度法进行简化，与强制反应位移法相同，均是为了规避弹簧刚度取值失真产生较大的计算误差。首先，通过自由场计算给出地震荷载下结构顶板和底板所处土层的最大位移差，然后把该时刻模型中全部土层的加速度取出，最后将该加速度结果通过水平体力的方式赋予整个模型土体和地下结构，通过静力的方法给出结构响应，其计算模型如图4所示。近年来，反应加速度法在国内得以大力推广，《城市轨道交通结构抗震设计规范（GB 50909—2014）》首次引入了反应加速度法。

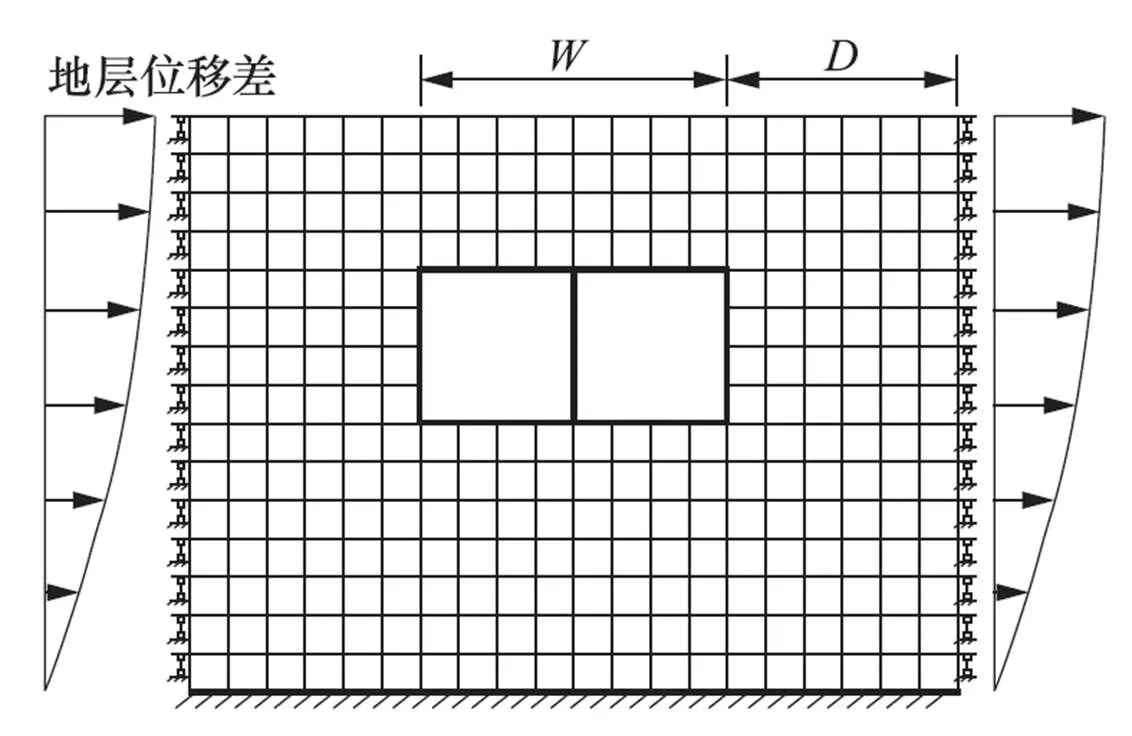
图3 强制反应位移法模型

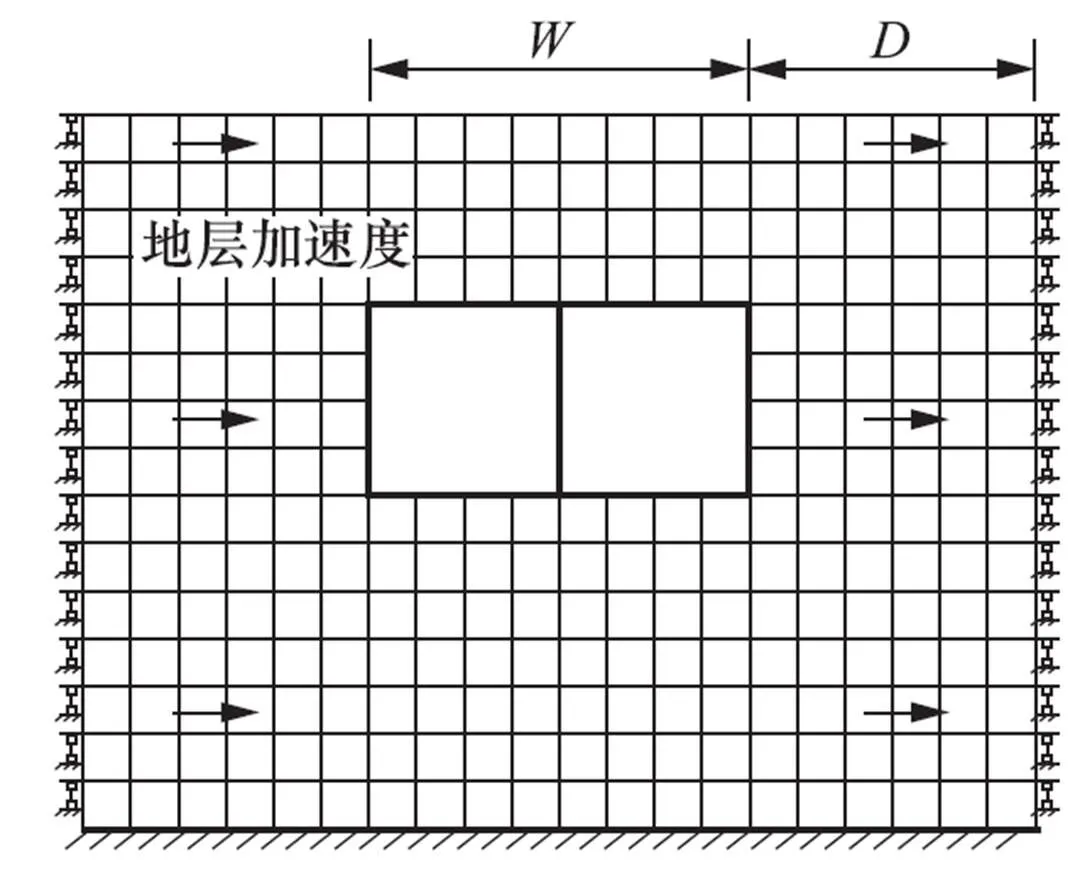
图4 反应加速度法模型

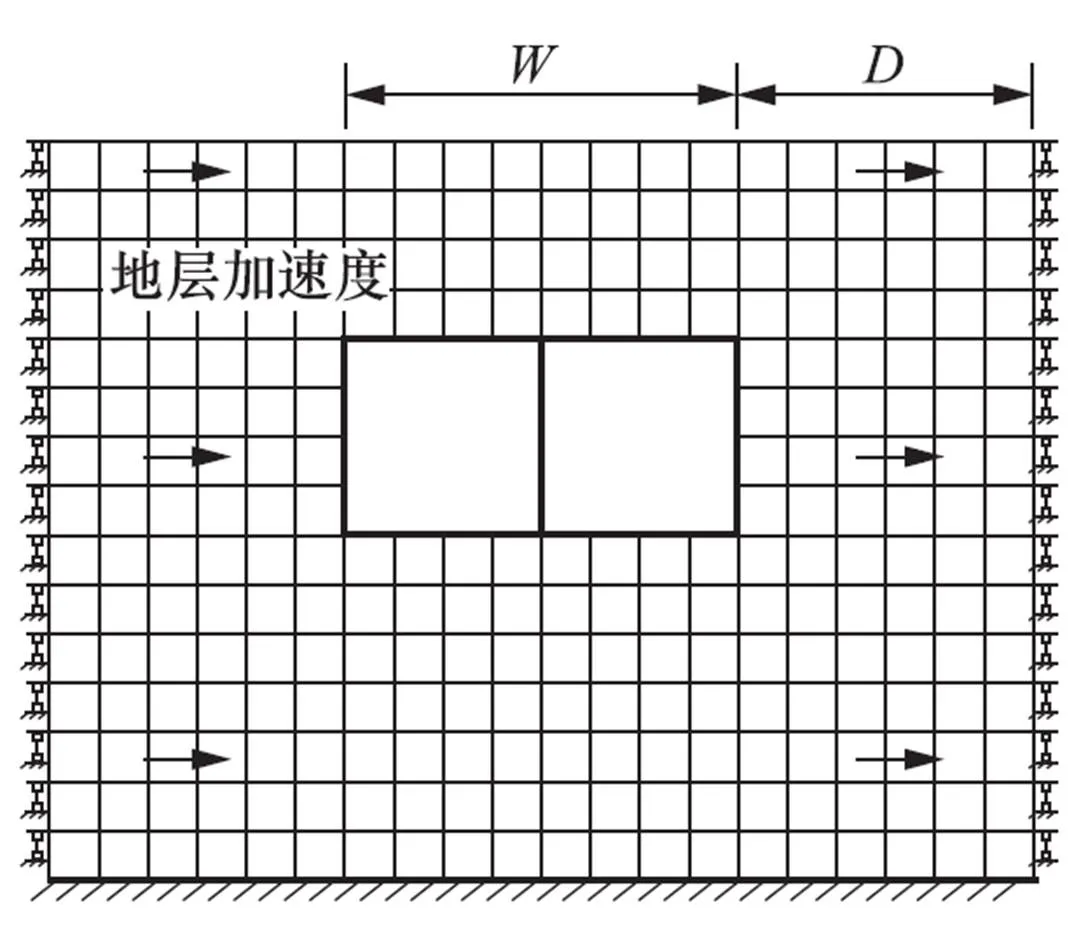
图5 仅在土体施加加速度的简化方法

1.5 仅在土体施加加速度的简化方法

Tateishi（2005）提出了强制反应位移法的改进方法，对整个土层强制施加水平体力从而让土层变形与自由场变形一致，即仅把水平加速度按体力的形式施加到土体上。仅在土体施加水平加速度也是对反应加速度法的进一步简化，计算求解的过程和反应加速度法一致，唯一的区别在于反应加速度法把最大变形状态时的土层加速度以体力的形式施加到土体和结构上，而该方法则进一步简化了这一处理过程，其模型见图5。由于地下结构一般内部挖空，仅有周围一圈衬砌，纵向单位长度的隧道质量远远小于原土体的质量，加速度在结构上产生的体力较小，因此理论上对结构的地震响应影响甚微（杨智勇等，2012）。

2 算例分析

2.1 模型建立

以某单一土层中埋深7m的双跨箱形地下结构为算例，计算其在地震荷载下的响应，该地下结构横截面尺寸为8m×4m，墙厚0.8m，中柱厚0.8m。依次采用动力时程法、反应位移法、强制反应位移法、反应加速度法和仅在土体施加加速度这5种方法计算该地下结构的内力和中柱顶底相对变形。本例中结构的横截面抗震分析可按平面应变问题处理，土-结构接触面采用ABAQUS软件中自带的绑定接触，土体与结构参数见表1。使用实体单元对土体进行建模，地下结构则使用梁单元进行建模并与土体连接，土体选取摩尔-库伦本构模型，结构则取为线弹性本构模型。

表1 土体与结构的物理力学参数

采用动力时程分析法时，分别将结构宽度和高度的4倍取为侧边距和底边距，计算结果用作校核，模型见图6、图7。反应位移法不建立土体，改变模型尺寸进行强制反应位移法、反应加速度法和仅在土体施加加速度方法的试算。

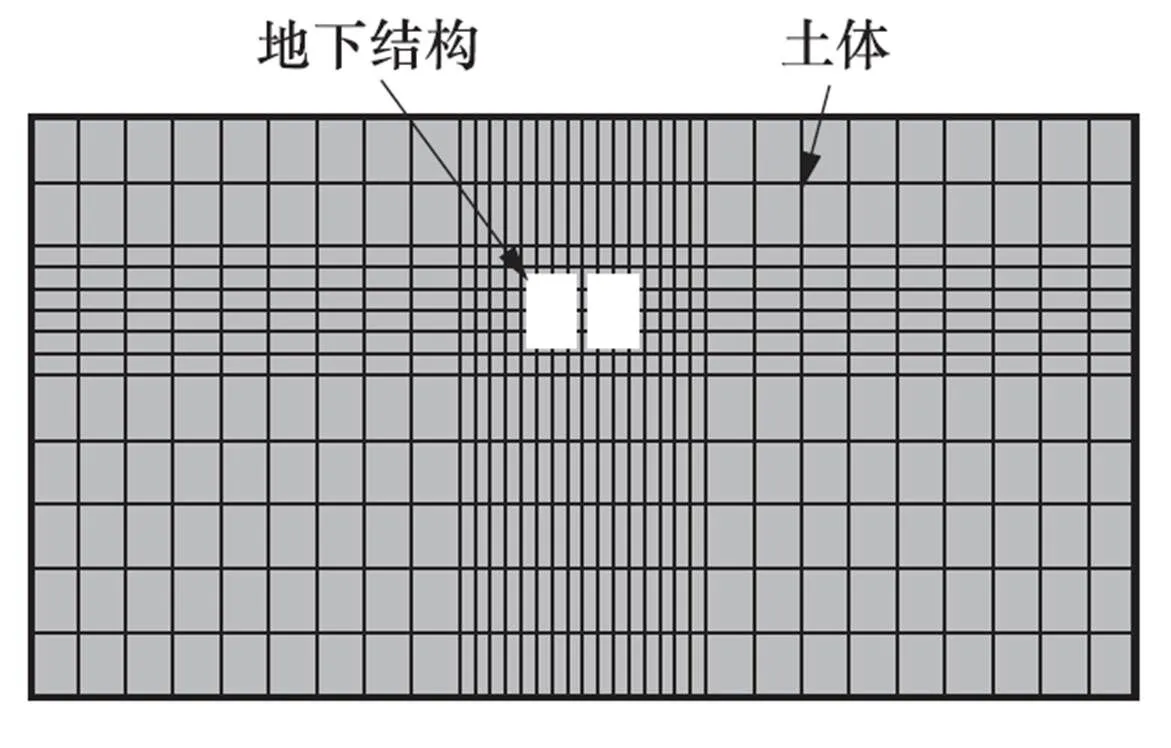
图6 二维土-结构动力时程模型

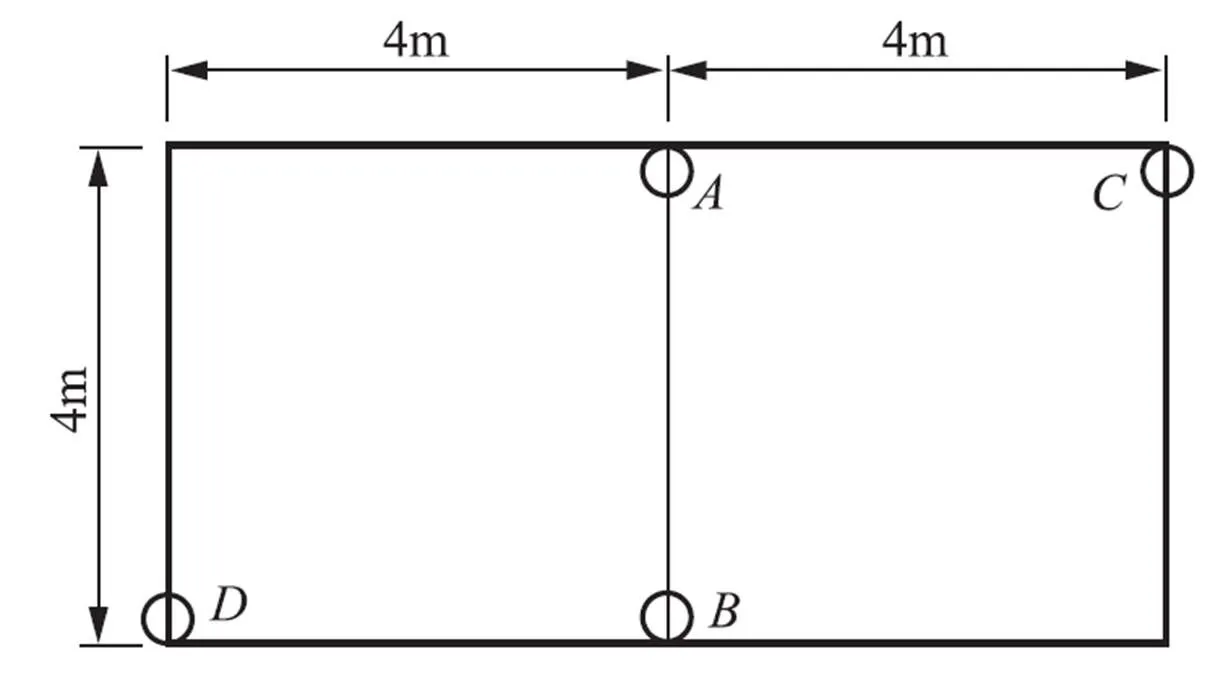
图7 结构尺寸与控制截面

采用动力时程分析法时，侧边界固定竖向、水平向释放，底边界为粘性边界，从模型底部输入峰值加速度为0.2g的El-Centro波，如图8所示。然后，再采用峰值加速度为0.2g的Kobe波（图9）验证分析所得的规律。自由场模型与土-结构动力时程分析模型采用相同的土体本构模型和土体参数，0.2g峰值加速度下土层位移差最大时刻的相对位移分布和加速度分布见图10、图11。

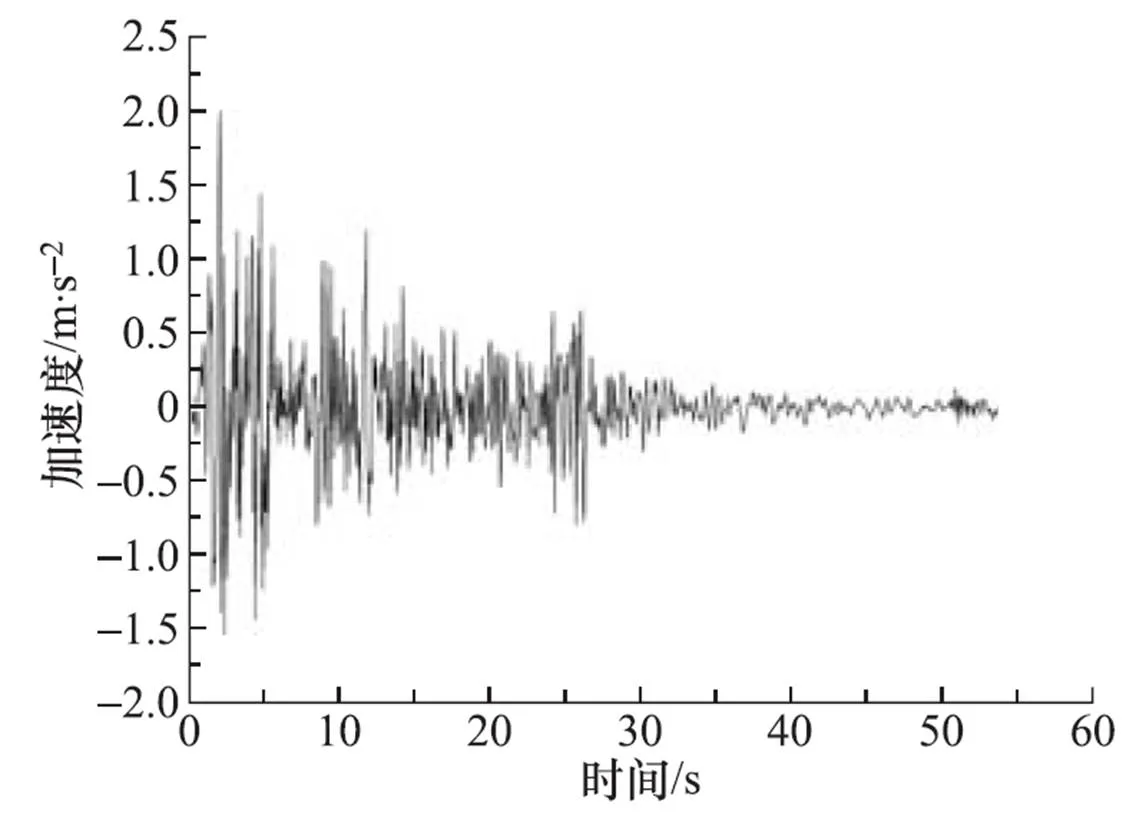
图8 El-Centro地震波

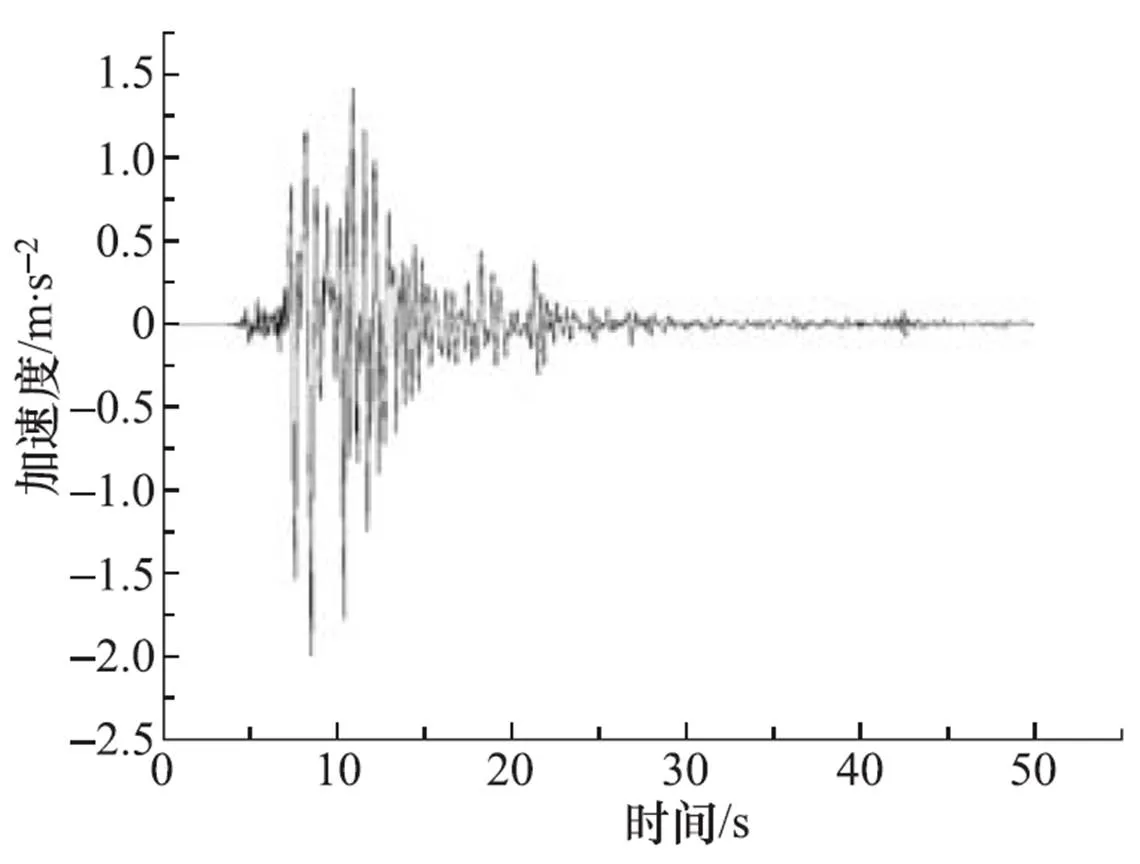
图9 Kobe地震波

2.2 结构响应分析

2.2.1 El-Centro波下不同侧边距结果分析

首先，以计算出1的动力时程分析法结果作为后续简化分析方法的校核标准。根据《城市轨道交通结构抗震设计规范（GB 50909—2014）》要求，动力时程分析的侧边距应大于结构宽度的3倍及以上，本次计算模型侧边距取为结构宽度的4倍；其次，采用反应位移法单独建立梁-弹簧单元对结构响应进行分析；最后，改变模型土体尺寸，用3种需要建立土体的简化分析方法对结构响应进行计算。输入峰值加速度为0.2g的El-Centro波，则控制截面、、、的弯矩、剪力和顶、底相对位移计算结果见表2、表3和表4，地下结构计算误差分析见图12。

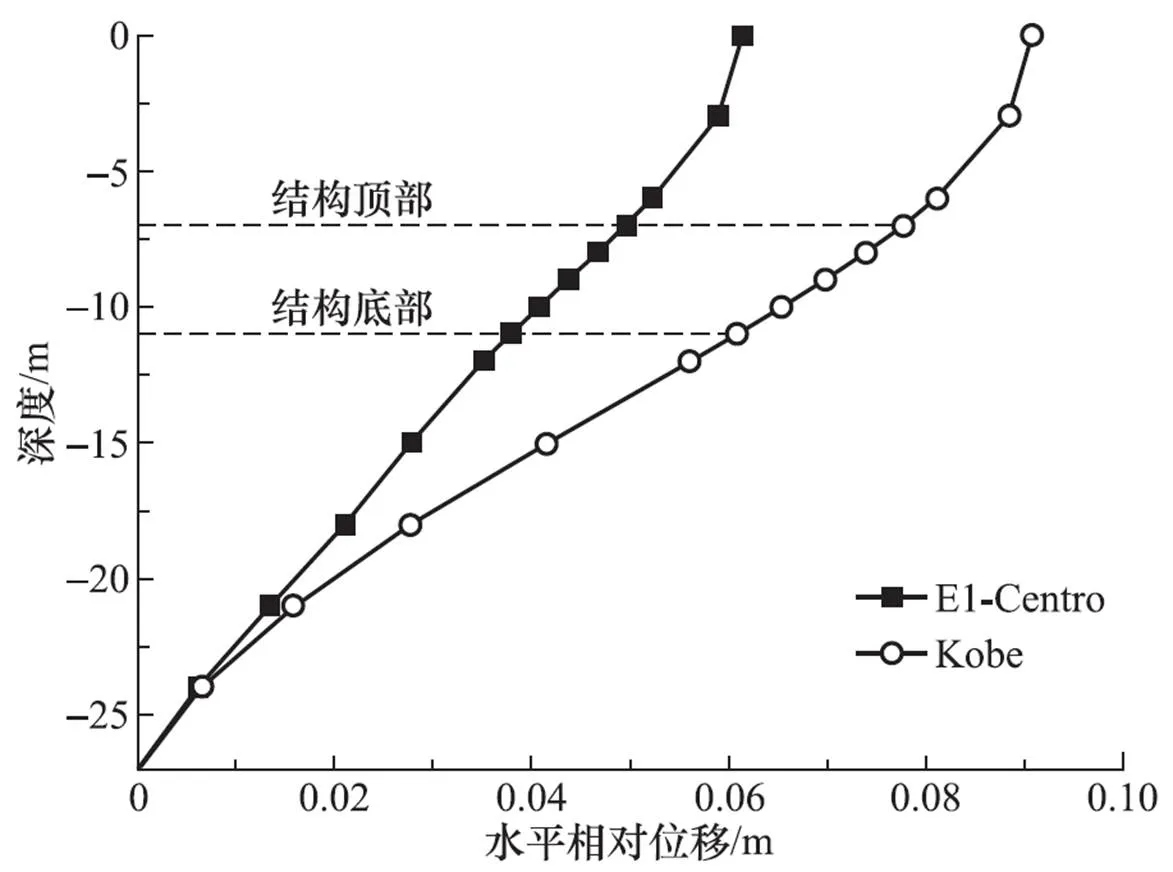
图10 自由场最不利水平相对位移分布

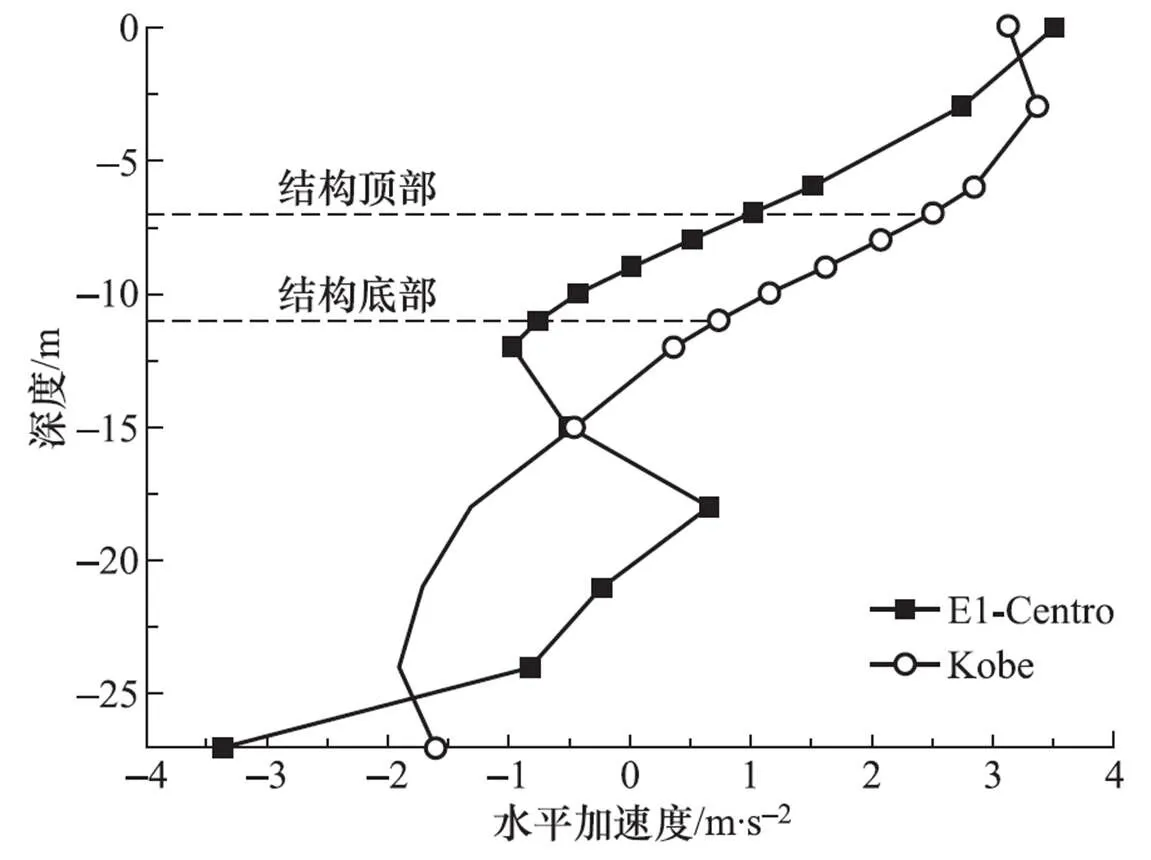
图11 自由场水平加速度分布

在输入0.2g峰值加速度El-Centro波的情况下，反应位移法的计算精度在结构中柱部分较好。对比反应位移法和动力时程分析方法可知，弯矩误差在中柱上端为1.41%，下端最小仅为0.34%，剪力误差在中柱上端最小仅为0.51%，下端为1.32%。但是在结构的角部，计算误差较大，剪力和弯矩计算值都偏小，在截面（右侧墙上端）弯矩误差值达到26.18%，剪力误差值达到45.25%，尤其截面（左侧墙下端），弯矩误差值最大达到42.12%，剪力误差值最大达到60.17%。弯矩平均误差为13.8%，剪力平均误差23.3%。

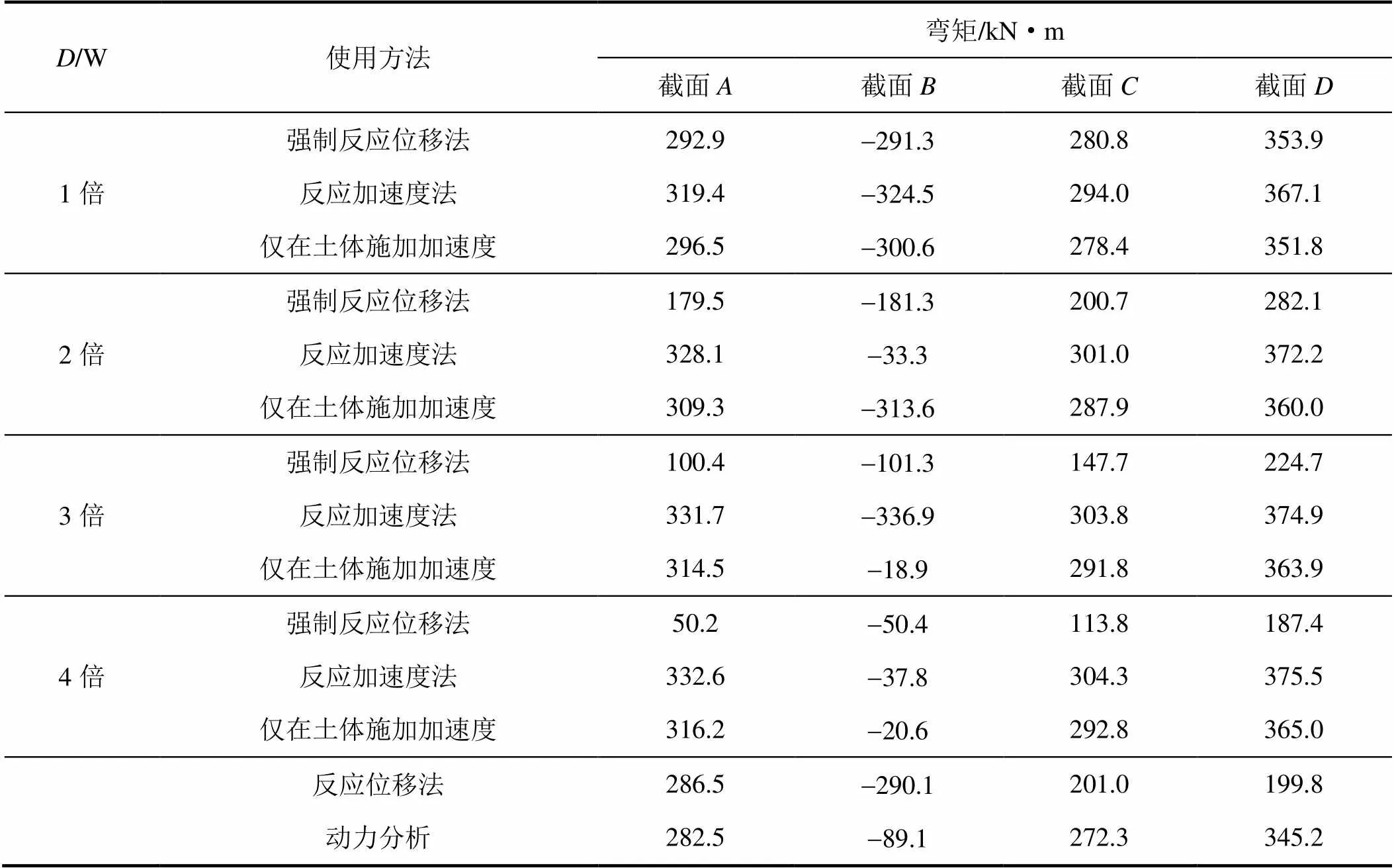
表2 不同侧边距的弯矩计算结果

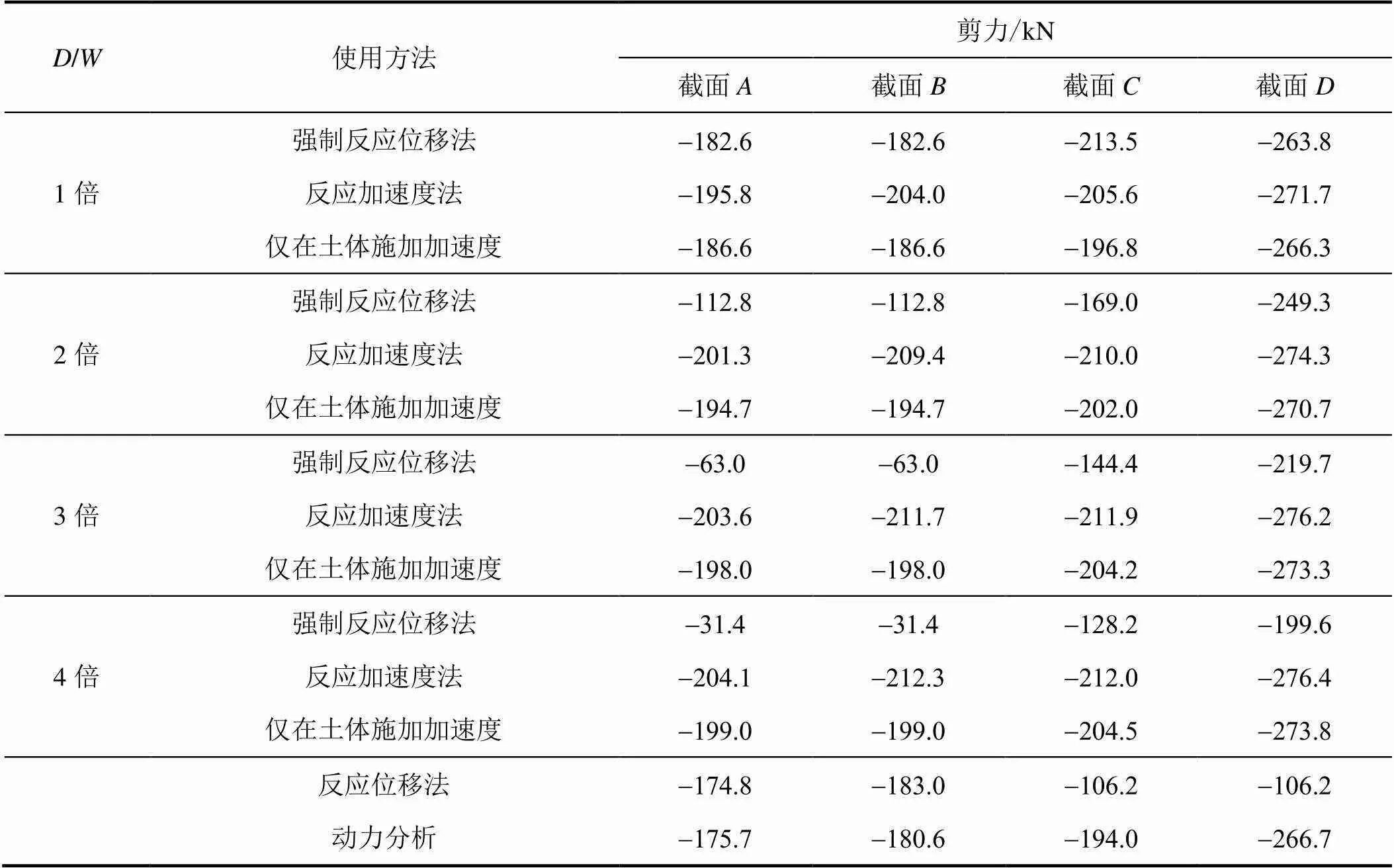
表3 不同侧边距的剪力计算结果

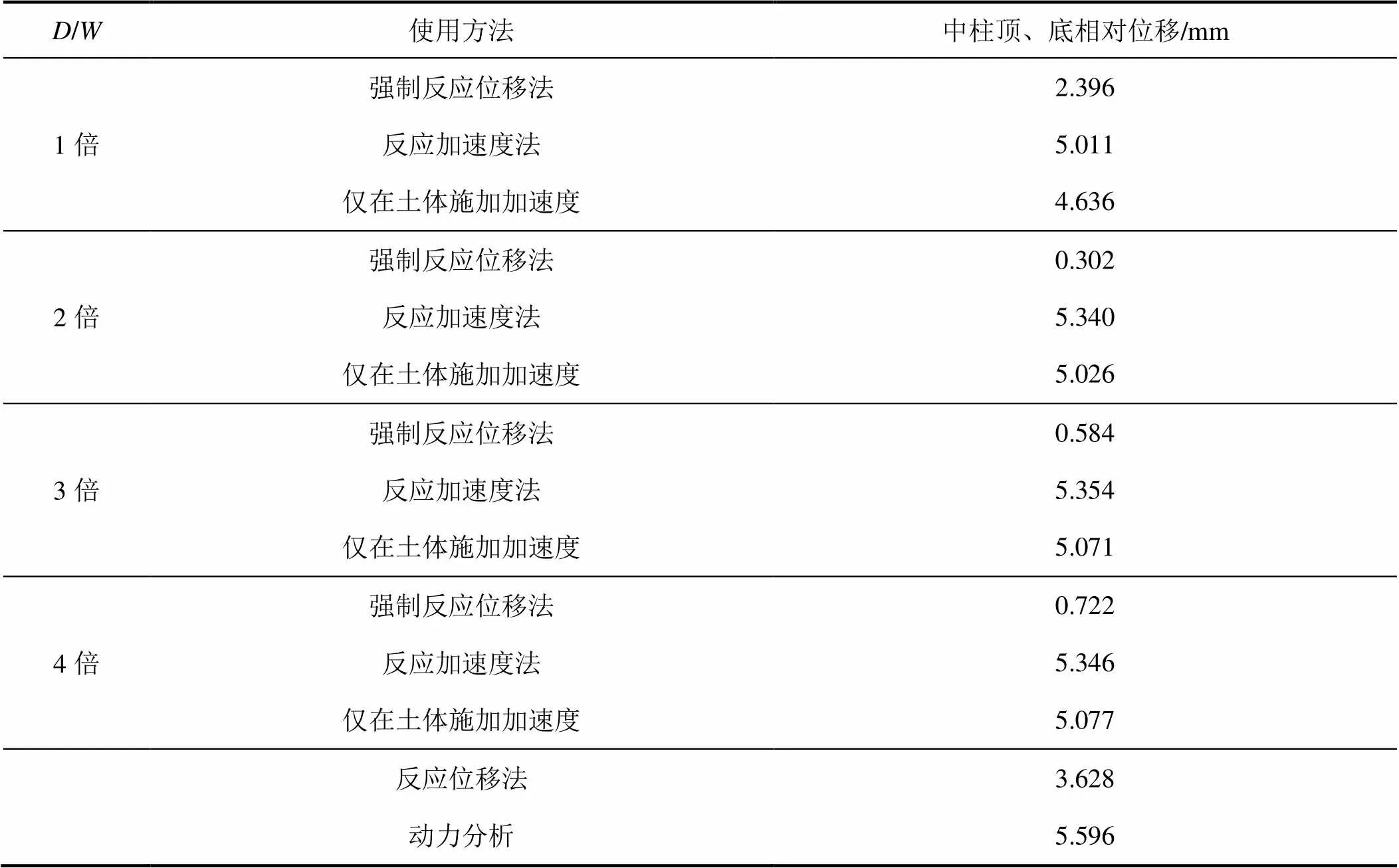
表4 不同侧边距的结构变形计算结果

强制反应位移法的计算精度依赖于静力模型土体侧边距的选取，随着土体侧边距取值的不断增加，地下结构的弯矩、剪力计算误差会相应的增大。当侧边距取为4倍结构宽度时，弯矩平均误差最大达到70.2%，剪力平均误差最大达到58.1%；然而，当侧边距取为1倍结构宽度时，弯矩平均误差仅为2.8%，剪力平均误差为2.5%。当侧边距为1倍结构宽度时，中柱顶、底相对变形误差为57.18%，侧边距为2倍结构宽度时误差最大为94.60%，但随着侧边距的增大，误差有所减小。

反应加速度法与仅在土体施加加速度的简化分析方法计算所得弯矩、剪力和中柱变形随着模型侧边距的增大，计算误差变化幅度很小。当侧边距取为1倍结构宽度时，反应加速度法的弯矩平均误差为10.1%，剪力平均误差为8.7%，中柱变形误差为10.5%，仅在土体施加加速度方法的弯矩平均误差为3.1%，剪力平均误差为2.4%，中柱变形误差为17.2%；当侧边距取为4倍结构宽度时，反应加速度法的弯矩平均误差为14.3%，剪力平均误差为12.7%，中柱变形误差为4.5%，仅在土体施加加速度方法的弯矩平均误差为9.2%，剪力平均误差为7.8%，中柱变形误差为9.3%。由此可见，以加速度模拟地震作用时土体侧边距对计算误差影响较小，2种方法变化趋势基本同步。由于仅在土体施加加速度的简化分析方法忽略了结构加速度，相同工况下该方法的计算数值略小于反应加速度法。施加加速度的2种方法对于结构变形的计算精度均较高，反应位移法次之，强制反应位移法的计算结果较不理想。

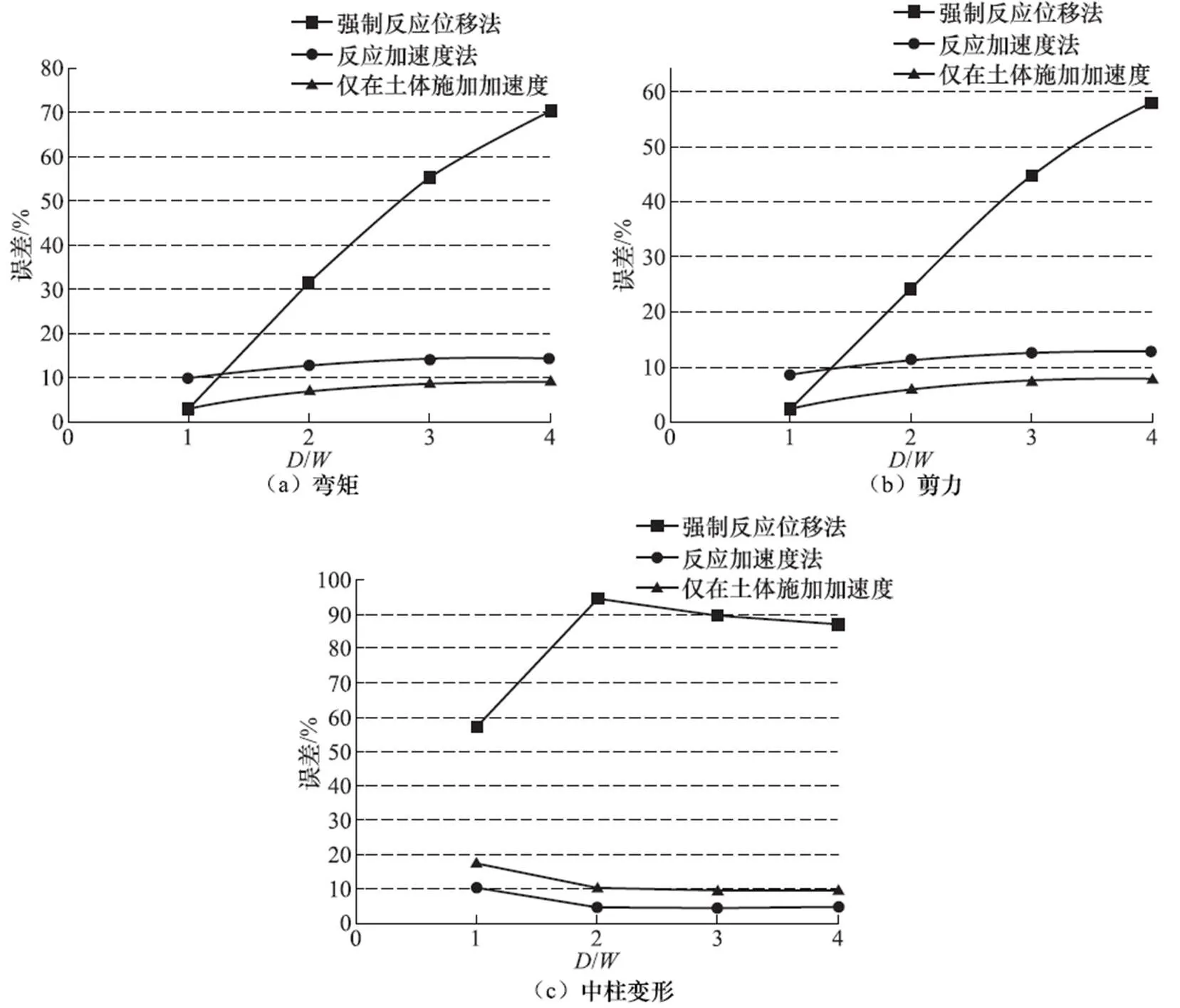
图12 3种带土体简化分析方法的计算误差

2.2.2 Kobe地震波验证分析

为了消除地震动不同带来的偶然性，改用0.2g峰值加速度的Kobe地震波验证上述分析规律。

从前文分析可知，反应位移法在应用过程中不需要建立土体；强制反应位移法在侧边距取为1倍结构宽度时计算误差较小；反应加速度法和仅在土体施加加速度的简化方法对于侧边界取值不敏感。因此，需要建立土体的3种静力模型统一采用1倍结构宽度作为侧边距。弯矩、剪力、中柱变形计算结果见表5、表6、表7。

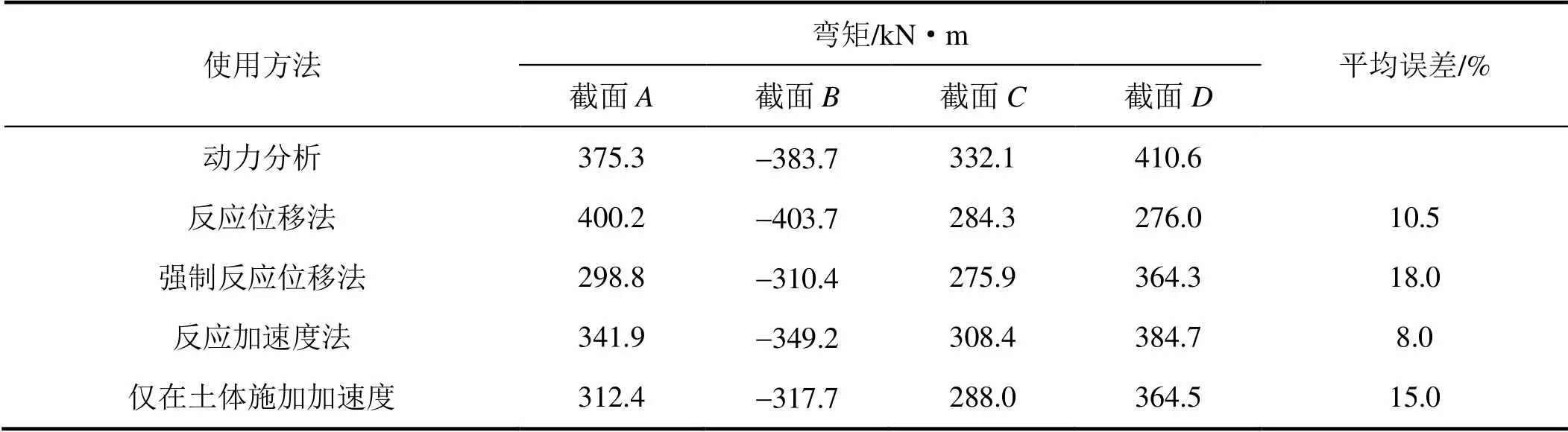
表5 Kobe波下弯矩计算结果

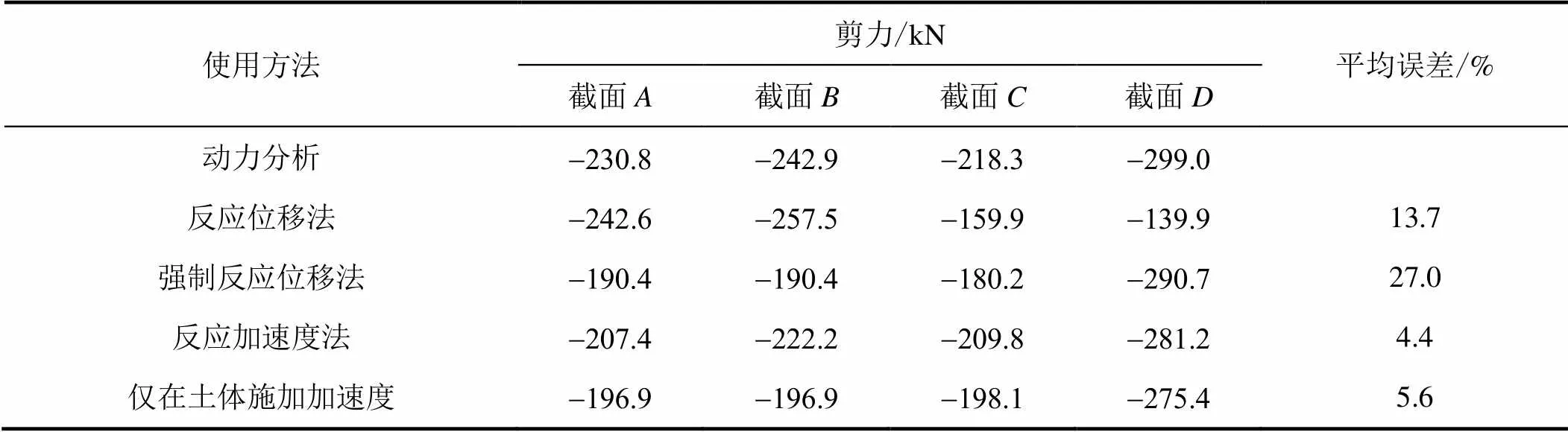
表6 Kobe波下剪力计算结果

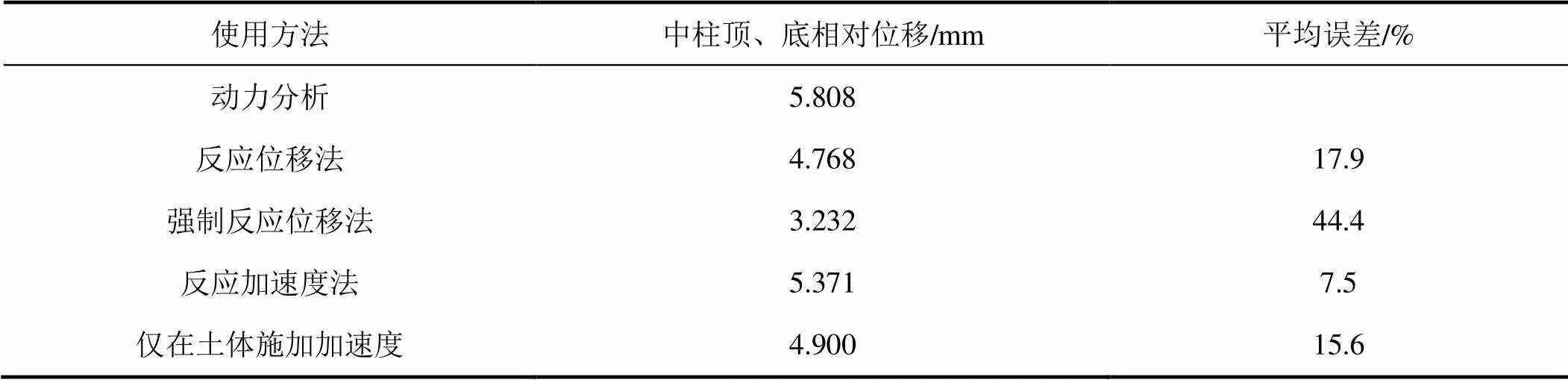
表7 Kobe波下结构变形计算结果

对于不同类型的地震动，4种简化分析方法的计算精度均比较稳定，弯矩误差在10%左右，反应加速度法平均弯矩误差最小，为8.0%，强制反应位移法平均弯矩误差最大，为18.0%；2种施加加速度简化分析方法的剪力误差极小，分别为4.4%和5.6%，强制反应位移法剪力误差最大，仅为27%；强制反应位移法的结构变形误差最大达到44.4%，其余3种方法精度较好，反应加速度法误差最小，仅为7.5%。

3 4种简化分析方法的特点分析

4种简化分析方法的相同点在于脱离了动力分析，能够按静力的方式计算结构响应，使得计算效率大大提高，且在不同地震动输入条件下都能得到较好的精度；另外，4种简化分析方法均需要进行自由场动力时程分析，从而获取地层位移或者地层加速度作为静力计算的地震输入荷载，自由场变形是4种简化分析方法的基础，但是结构存在对自由场的影响却被忽略了。

4种简化分析方法的不同点在于，①采用反应位移法不需要建立模型土体，以弹簧单元模拟土-结构相互作用，但是地基弹簧刚度取值需要进行6次有限元计算，过程比较繁琐。并且，土体弹簧刚度值对结构内力计算有巨大影响，通过有限元计算弹簧刚度的方法无法反应土层自身的相互作用，计算过程中土体的等效弹簧之间是不相关的，造成的结果则是土层对结构特别是角部的约束作用减小，计算所得的角部内力值偏小。②强制反应位移法对静力模型侧边界宽度值的选取非常敏感，侧边距的选取对于结构内力计算精度有重大影响。从计算结果来看，采用1倍结构宽度作为侧边距时结构内力的计算误差最小。但是无论侧边距如何变化，对结构变形的计算误差均较大。在对结构内力进行校核时，采用该方法计算的结果较为可靠。③反应加速度法和仅在土层施加加速度的简化方法对于侧边界的选取不敏感，2种方法对于不同的侧边距得到的计算精度均比较稳定，计算精度随着侧边距的增加仅有轻微的变化，2种方法对结构内力、变形的计算误差均较小。

4 结论

本文通过反应位移法、强制反应位移法、反应加速度法和仅在土体施加加速度4种简化分析方法，分别计算了1个双跨箱形地下结构在0.2g峰值加速度的EL-Centro波和Kobe波作用下的地震响应，再利用时程分析法进行校核，经过对比，得出以下结论：

（1）总体而言，4种简化分析方法计算得到的结构在地震作用下的内力、变形值接近，规律一致，不同类型的地震动作用下均能得到较好的计算精度，能合理地反映地下结构的动力特性。

（2）若要进一步推广使用反应位移法，则须使其基地弹簧系数的取值快捷、可靠。

（3）模拟地震等效荷载的自由场土层位移和土层加速度具有较好的计算精度，且便于施加，但是需要进一步考虑地下结构存在对自由场的影响。

（4）在使用强制反应位移法进行结构内力校核时，侧边距取为1倍结构宽度时效果最好，计算误差最小。而反应加速度法和仅在土体施加加速度的方法对侧边距的选取不敏感。

（5）强制反应位移法、反应加速度法和仅在土体施加加速度3种带土体模型的简化分析方法均省略了反应位移法中地基弹簧刚度系数的取值，同时更加真实地反应了土-结构间的协调作用，使用时比反应位移法更简便。

陈国兴，陈苏，杜修力等，2016．城市地下结构抗震研究进展．防灾减灾工程学报，36（1）：1—23．

陈晓强，钱七虎，2010．我国城市地下空间综合管理的探讨．地下空间与工程学报，6（4）：666—671．

川岛一彦，1994．地下构筑物の耐震设计．日本：鹿岛出版会．

林皋，1990a．地下结构抗震分析综述（上）．世界地震工程，（2）：1—10．

林皋，1990b．地下结构抗震分析综述（下）．世界地震工程，（3）：1—10，42．

刘晶波，刘祥庆，李彬，2008．地下结构抗震分析与设计的Pushover分析方法．土木工程学报，41（4）：73—80．

刘晶波，王文晖，赵冬冬等，2013．地下结构抗震分析的整体式反应位移法．岩石力学与工程学报，32（8）：1618—1624．

刘如山，胡少卿，石宏彬，2007．地下结构抗震计算中拟静力法的地震荷载施加方法研究．岩土工程学报，29（2）：237—242．

片山幾夫，足立正信，嶋田穰等，1985．地下埋設構造物の実用的な準動的解析手法「応答震度法」の提案．土木学会年次学術講演会講演概要集，（40）：737—738.

钱七虎，2017．推进城市地下空间规划建设的思考．城乡建设，（18）：60—65．

权登州，王毅红，井彦林等，2015．黄土地区地铁地下结构抗震研究综述．震灾防御技术，10（3）：565—574．

同济大学，2009．DG/TJ 08-2064-2009地下铁道建筑结构抗震设计规范．上海：上海市建筑建材业市场管理总站.

杨智勇，黄宏伟，张冬梅等，2012．盾构隧道抗震分析的静力推覆方法．岩土力学，33（5）：1381—1388．

中华人民共和国建设部，2006．GB 50111—2006 铁路工程抗震设计规范．北京：中国计划出版社.

中华人民共和国住房和城乡建设部，2014．GB 50909—2014 城市轨道交通结构抗震设计规范．北京：中国计划出版社．

Hashash Y. M. A., Hook J. J., Schmidt B., et al., 2001. Seismic design and analysis of underground structures. Tunnelling and Underground Space Technology, 16(4): 247—293.

Iida H., Hiroto T., Yoshida N., et al., 1996. Damage to daikai subway station. Soils and Foundations, 36(S): 283—300.

Penzien J., 2000. Seismically induced racking of tunnel linings. Earthquake Engineering Structural Dynamics, 29(5): 683—691.

Tateishi A., 2005. A study on seismic analysis methods in the cross section of underground structures using static finite element method. Structural Engineering, 22(1): 41—53.

Wang J. N., 1993. Seismic design of tunnels: a simple state-of-the-art design approach. New York: Parsons Brinckerhoff Quade and Douglas Inc.

Comparison of Four Simplified Analytical Methods for Seismic Design of Underground Structures

Xu Kunpeng1), Jing Liping1)and Bin Jia2)

1) Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China 2) College of Civil Engineering, Hunan University of Technology, Zhuzhou 412000, Hunan, China

The theoretical basis of the simplified analytical method for seismic design of underground structure is that the deformation of underground structure depends on the deformation of foundation soil during earthquake, which fails to reflect the dynamic characteristics of the structure. Based on the most commonly used seismic displacement method, three kinds of simplified analytical methods are discussed in this paper. The forced displacement method is by applying the ground deformation to the boundary of the soil finite element model to simulate seismic load. The response acceleration method is by applying the ground acceleration to the integral finite element model to simulate seismic load. The third method is only by applying the ground acceleration to the soil finite element model to simulate seismic load. The above three simplified analytical methods can avoid calculating the value of the spring stiffness and improve the computational efficiency. Taking a double-span box structure as example, the calculations by applying three kinds of simplified analytical methods above with different lateral margins are carried out, and the analysis results are verified with the results of the dynamic time history method to calculate precisions. Combined with seismic displacement method, the error of four kinds of the simplified analytical methods is compared. The results show that the lateral margin should be equal to structure width when using the forced displacement method, and the response acceleration method and the method with only soil acceleration are not sensitive to the value of the lateral margin, and the error caused by the seismic displacement method reaches the maximum at the corner.

Underground structure; Quasi-static; Simplified analytical method; Lateral margin; Computational precision

10.11899/zzfy20190203

中国地震局工程力学研究所基本科研业务费专项资助项目（2017B10、2017B14），国家重点研发计划（2016YFC0800205），国家自然科学基金（51438004）

2018-10-17

徐琨鹏，男，生于1995年。硕士研究生。主要从事地下工程抗震研究。E-mail：iem_xkp@163.com

景立平，男，生于1963年。研究员。主要从事地下工程抗震研究及教学。E-mail：jing_liping@126.com

徐琨鹏，景立平，宾佳，2019．四种地下结构抗震设计简化分析方法对比．震灾防御技术，14（2）：281—292．