智能RGV的动态调度模型研究

徐晓龙，张商州，黄乐乐

（商洛学院电子信息与电气工程学院，陕西商洛 726000）

RGV（Rail Guided Vehicle）是与地面导向轨道接触式的运输车，根据运动方式的不同，可分为环形轨道式和非环形往复式[1]，根据设计功能的不同，简单的分为装配型和运输型两种。RGV 具有运行速度较快、性能稳定性较好等特点，分别应用于产品部件的装配和工厂中物料的运输，可大大提高运输和装配的能力[2-3]。本文研究的RGV 动态调度系统由8 台CNC（Computerized Numerical Control）、1 辆直线型轨道式自动引导车 RGV、1条RGV 直线轨道、1 条上料传送带、1 条下料传送带等附属设备组成。能够完成上下料及清洗物料等作业任务。针对本问题，有学者以最小化单个周期所用时间为目标，求解较优的调度方案使用Python2.7 实现算法[4]；有学者将问题转化为变相TSP 问题，采用改进的遗传算法进行模型的求解[5]。本研究在限定工作时间（8 h）内，以 CNC 加工一道工序和加工两道工序分别对RGV 的动态调度策略进行研究：加工一道工序以RGV 移动距离最短和加工物料最多为约束，加工两道工序，以加工过程逻辑性为约束，对两种情况分别建立多目标规划模型，求出RGV 的动态调度策略。

1 RGV的工作模式

一道工序的物料加工作业情况，每台CNC安装同样的刀具，物料可以在任一台CNC 上加工完成；两道工序的物料加工作业情况，每个物料的第一道和第二道工序分别由两台不同的CNC 依次加工完成。对一般问题，分别考虑一个班次（8 h）无故障，一道工序的物料加工作业和两道工序的物料加工作业时，两种工作模式下，RGV 的动态调度模型。系统示意图如图1所示，系统作业参数见表1。

2 RGV调度模型的建立

本文建立数学模型中，需要用到的符号见表2所示。

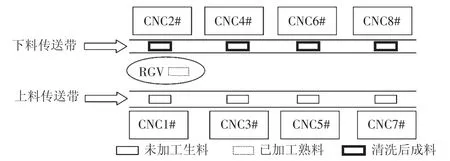
图1 智能加工系统示意图

表1 智能加工系统作业参数

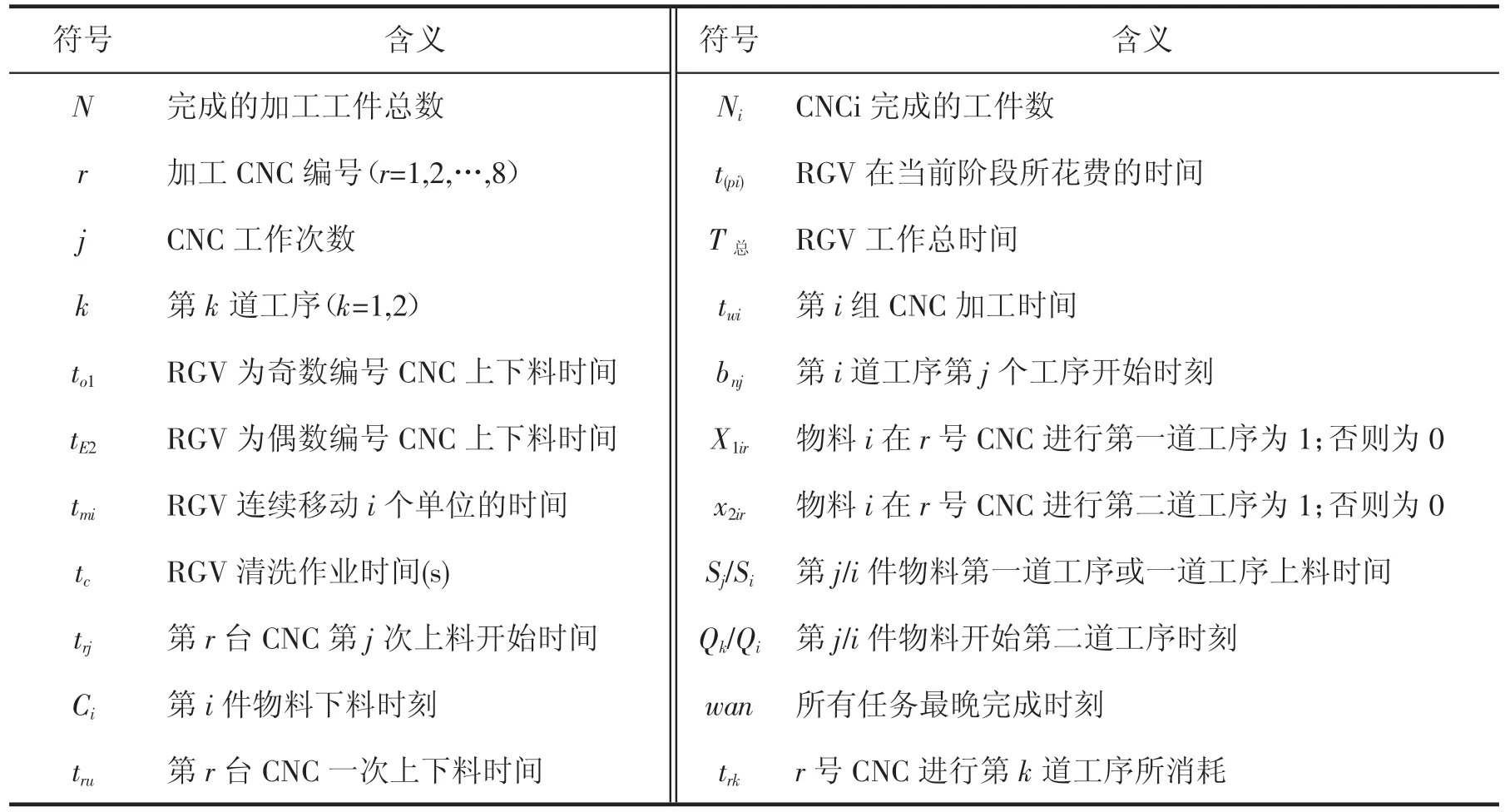
表2 符号说明

假设8 h 连续作业内8 台机器的作业车间调度问题需满足下列约束条件。

1）一个作业由若干道工序构成：移动RGV，上料、加工、下料、清洗等。

2）每道工序必须在指定的CNC 上加工。CNC 的每道工序从开始到结束不会被另外的工序所中断。

3）按照加工工艺的规定，每道工序必须在它前面的工序加工完毕后再加工。

一般性定义如下：

n 个工件的集合{p1，p2，…，pm}，8 台机器的集合为 r={r1，r2，…，r8}，注意 Mi，Mj(i≠j)可能是同一台设备，但所实现的工序内容不同。此处把实现同一功能的一类机器中的多台。

2.1 RGV只进行一道工序的建模

现为只需加工一道工序的物料在8 台CNCi=1～8，一共加工N 件产品，要使RGV 在8 h 内工作效率达到最大，则要求RGV 在此期间内移动最短的距离并且CNC 完成的工件数最多。

由于1#CNC 最先开始工作，即最先完成工作。

第1 台CNC 第j 次开始上料时间：

1）若物料加工时间大于给所有CNC 工作台都完成上下料时间，并且RGV 在加工第j 次前，能返回初始位置：

2）若物料加工时间小于给所有CNC 工作台都完成上下料时间，并且RGV 返回初始位置加工第j 次的时间为：

3）由于偶数和奇数的上下料时间不同且在CNC 第一次开始加工之前不需要清洗，则：

当j=1 时，CNC 上下料时间为：

当 j＞1 时，CNC 上下料时间为：

目标函数为：

(7)式中：TCNC为加工一个物料所需的时间；Mi=1～8为加工工件号；N 为表示完成的加工工件总数；j 为 CNC 工作次数；Ni完成的工件数；tij为第r 台 CNC 第j 次上料开始时间；T总为 RGV 工作总时间（s）；twi为第i 组 CNC 加工时间；t01为 RGV为奇数编号CNC 上下料时间；T(pi)为RGV 在当前阶段所花费的时间；tE2为RGV 为偶数编号CNC上下料时间；tc为RGV 清洗作业时间；tmi为RGV连续移动i 个单位的时间。

2.2 RGV进行两道工序建模

每台机器每次只能处理一个物料这一约束条件可理解为一旦开始顺序确定，则后续仍按原顺序进行。引入0～1 变量表示任意两工件相对生产顺序，对两个加工顺序依次进行比较，根据他们的相对加工顺序求物料加工总工序。

首先每个物料都要按照第一道工序，然后按照第二道工序进行加工。即第一道结束，才能进行第二道工序。

设bnj为第n 道工件第j 个工序开始时刻。每个零件加工顺序不变，即前一个加工结束才能加工下一个。

又由每个机器每次只能加工一个工件，第n+1 个工件必须在第n 个工件的j 工序完成后才能进行j 工序。

同一台CNC 不能进行两道工序。

约束条件，s.t.：

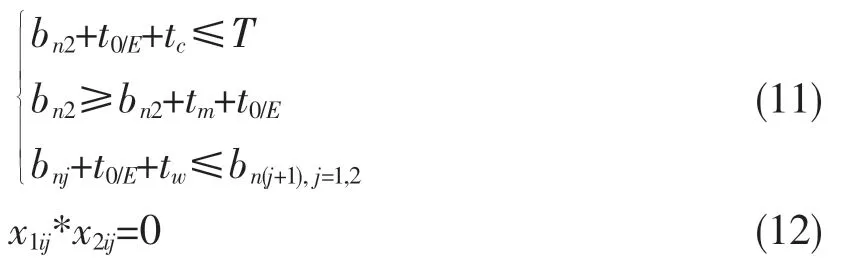
第i 件物料下料时刻需大于第二道工序开始时刻+8 台CNC 第一道工序时间+清理时间+上下料时间。

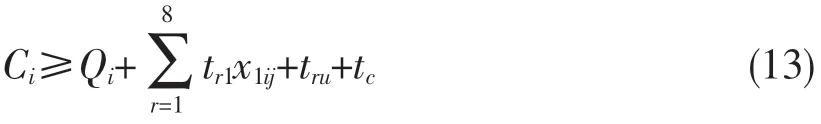
第i 件物料第二道工序开始时刻需大于第一道工序开始时刻+8 台CNC 第一道工序时间+清洗时间+上下料时间。综上可得目标函数：

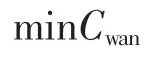
约束条件为：

3 RGV调度模型算法

3.1 RGV进行一道工序

由图1所示的智能加工系统示意图，规划出RGV 最佳路径，需要满足在 8 h 内（28 800 s 内）完成物料加工数最多，且RGV 移动路径最少，移动时间最少。在顺序排队原则的基础上提出了就近算法，结合策略设置方法来优化作业调度，以提高作业效率[6-7]。RGV 初始位置在CNC1#和CNC2#正中间，所以应该先给CNC1#和CNC2#上料，然后再移动RGV 到3，4#CNC，进行上料。再移动到5，6#CNC 进行上料，最后一个到 7，8#CNC 进行上料。假设加工时间远大于移动和上料时间，那么RGV 在完成8 台CNC 上料之后，应该返回初始位置等待CNC1#加工完成并开始CNC1#下料和清洗，以此类推。RGV 最优路径为1→2→3→4→5→6→7→8→1，往复循环。通过式(1)～式(7)，利用 C 语言，MicrosoftVisualC++编写 RGV 调度算法。运行程序，结果如图2所示。

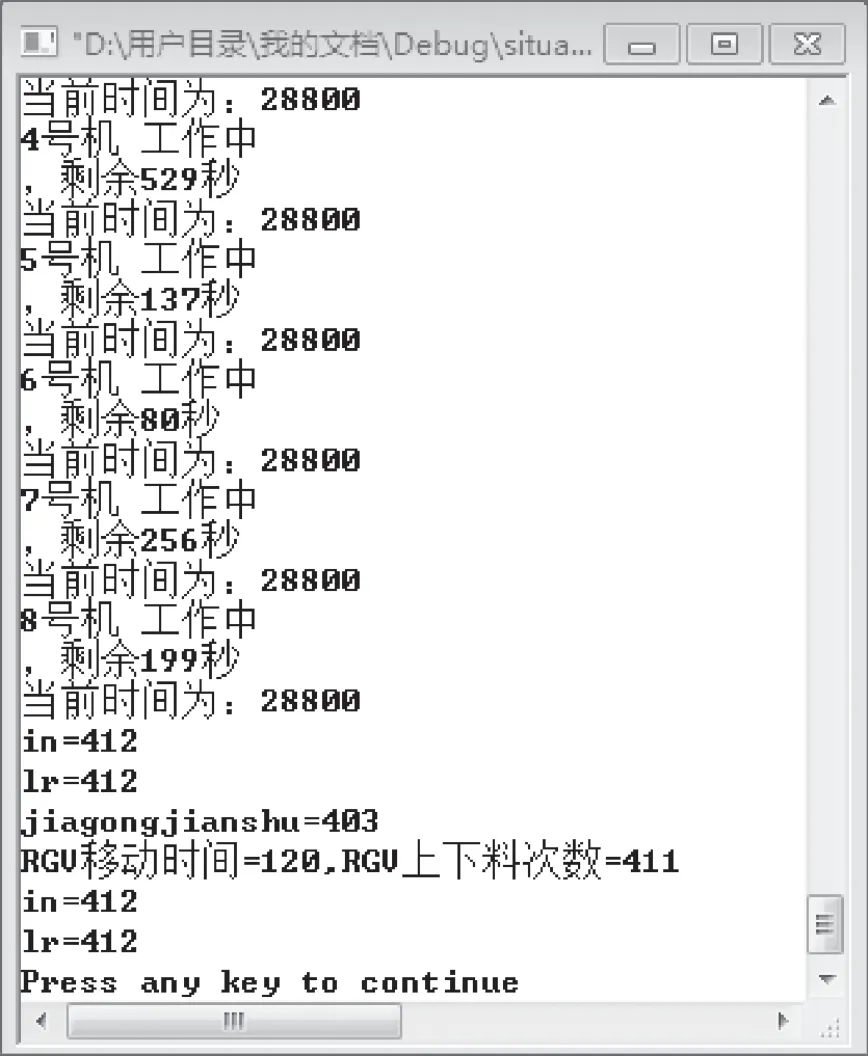
图2 第1 组物料加工程序运行结果

由图2可知8 h 内，RGV 上下料次数为411次，加工工件数为403 件。

3.2 RGV进行两道工序

两道工序的加工，每个CNC 加工过程中不允许换刀，且第二道加工工序需要在第一道工序完成之后进行，根据各工件加工顺序关系，依次用excel 求解各CNC 的上料开始和结束时间。假设奇数号CNC 加工第一道工序，偶数号CNC 加工第二道工序，则RGV 的最优路径为CNC1→3→5→7 上料加工第一工序，再返回依次给CNC2→4→6→8，加工第二工序。加工顺序如图3所示。

图3 两道工序RGV 调度甘特图

4 RGV调度模型的评价

模型的优点： 本研究运用了数学函数求和公式建立模型，模型建立后的求解过程严密，严谨，可信度较高；使用甘特图，使问题更加清晰，各CNC 工作时间，加工进度一目了然；系统的作业效率从整体上评价了不同生产顺序的利弊；这个算法的优点就在于它的思路简单，有效性良好[8-11]。一环套一环，从一道工序到两道工序，只有将第一个模型建立好，才能接下来解决后面的问题，逻辑性强[12]。

模型的缺点：所建立的模型对工件个数少的动态调度比较适用，当工件个数很多很难得到全局最优解；模型没有考虑到成本问题，只考虑到了完成所有的工件所用最短时间。对于加工过程中CNC 出现故障或者增加CNC 数量等复杂情况并未进行考虑。

本研究得出的结论：以RGV 给CNC 上下料问题研究RGV 动态调度，运用多目标优化数学建模方法，以式(6)最多加工物料为目标函数，以式(7)为约束，建立整数规划模型，通过求解得到RGV 最优路径为：1→2→3→4→5→6→7→8→1循环上料、加工、下料、清洗；另一方面：对于加工两道工序的情况，以最多加工物料为目标函数，以式(14)为约束，建立整数规划模型，通过求解得到 RGV 最优路径为：RGV 依次给 CNC，2→4→6→8 上料加工第一工序，再返回依次给CNC，1→3→5→7 加工第二工序，往复循环。本研究可以给RGV 动态调度的研究提供一定参考。