基于STL模型的解析处理和几何特征精度评价研究

徐思远，杨伟群

（北京航空航天大学 机械工程及自动化学院，北京 100191）

0 引言

3D打印技术（3D Printing），也被称为增材制造技术（Addtive Manfacturing，AM）。美国材料与试验协会（ASTM）于2009年成立了3D打印技术委员会（F42委员会），该委员会随后给出了3D打印技术的明确定义：3D打印技术是一种与传统的材料加工方法截然相反，基于三维CAD模型数据，通过增加材料逐层制造的方式。

由于STL模型文件是多数快速原型系统所应用的标准文件类型，在不同平台转换时通用性更高，故对该类型文件的研究显得尤为重要。STL文件格式简单，具有高可重用性，高性能，高移植性，跨平台的优点。但同时也正因为格式简单造成了存储的信息不够，其中的拓扑结构信息、尺寸信息、特征信息都需要利用反向工程求解。本文基于STL模型文件，重建模型拓扑结构、进行模型缺陷检测、提取拟合模型特征并进行公差的计算，并提出一种可以应用于3D打印技术的质量表征技术。

1 重建STL模型拓扑结构

1.1 STL文件介绍

STL（Stereolithography）是由3D Systems公司开发一种文件格式，最早出现在该公司开发的光固化成型技术的CAD软件中。STL格式将零件的表面分解为无数的小三角面片，每个三角面片有三个顶点和一个法向量组成，法向量垂直于三角面片指向零件外侧。如图1所示，图1(a)是三角面片的数据结构：法向量和顶点都是由笛卡尔坐标系中x、y、z三个坐标组成，在三角面片的内部存储中第一个是法向量，随后是三个顶点，顶点的排列顺序没有规定。图1(b)是三角面片的示意图。

图1 STL文件中的三角面片

1.2 重建拓扑结构

由于三角化算法的局限性，导致STL数据模型有以下不足：用小三角形面片近似实体表面降低了精度；因STL模型中各三角形面片间没有拓扑信息，三角形面片间的公用结点需要多次存储；没有表示STL数据模型三角形面片之间的邻接关系；为提高精度多个三角形面片进行近似时，很可能出现某个顶点的分离。

为了在缺陷检车和特征拟合阶段可以高效的访问到模型的面片拓扑信息，必须重新建立模型的拓扑结构，保存点、线、面的邻接关系、所属关系。图2是点、线、面的数据结构。

图2 点、线、面的存储数据结构

从数据结构中可以看出，在点、线、面的数据中各自存储了所属的上级特征和所包含的下级特征，建立了点-边关系、点-面关系和边-面关系，得到了模型数据的拓扑关系，为分析算法提供了数据结构基础。

由于一个三角面片中含有三个顶点，每一个顶点又可以存在于不同的若干个三角面片中，因此有顶点的重复存储，从STL文件中读出的三角面片顶点数据是冗余的，这样会浪费存储空间，也有可能造成数据的不一致错误，因此在建立拓扑结构的过程中，完成了冗余点的剔除，使得算法更加简洁高效。

2 模型缺陷检查

为了保证拟合程序的顺利进行，必须确保STL模型的正确性。所以对模型的缺陷检查尤为重要，本章阐述了STL模型文件的常见缺陷及检测算法。

2.1 STL模型缺陷描述

STL模型是通过对三维实体模型进行表面三角面片离散得到的，只能在一定精度上实现与理论模型的配准。在CAD造型中，文件常常需要在多个CAD软件之间进行转换。由于软件之间实现方式的差异以及二进制文件中由于数据精度造成的四舍五入偏差，STL文件往往会出现各种各样的缺陷及异常。这会在文件处理和打印处理时造成异常，甚至直接反映在打印成品上，造成质量缺陷。

STL模型需要遵循以下规范：1）共定点规则，三角面片需要与邻近面片有重合的两个顶点；2）取向规则，面片的法向量必须遵循右手定则，并且不可以指向实体内部；3）充满规则，三角面片必须连续充满实体表面。

在此规范基础上，STL模型常见的缺陷有空洞、法向量反向、缝隙与重叠、错位、多余、不共顶点等。图3为常见缺陷示意图。

图3 常见缺陷示意图

2.2 STL模型缺陷检测

1）法向量反向：由于三角面片中顶点记录顺序混乱，有可能造成法向量的错误，以至于实际的法向量与已经记录的三角面片的法向量不一致的情况出现，因此有必要设计算法检测法向量反向的错误。

由于法向量严格遵守右手定则，故可以根据三顶点确定的符合右手定则的向量与文件中的法向量比较，方向一致则为正确的法向量。首先由三个顶点得到两个向量，计算两个向量的叉积可得到复合右手定则的法向量。将得到的法向量与原法向量进行点积计算，若结果大于零则可确定该处法向量没有发生反向错误。依次计算每个三角面片的法向量。

2）悬边和悬面检测：悬边是由于数据误差或面片丢失导致所属面只有一个的边。悬面是由于三角面片丢失造成连接面少于三个的面片。由于拓扑关系的建立，这两个缺陷的检测相对容易。只需要将边结构中的e_faceId.size()和面结构中的neighborFaceId.size()取出来判断即可。

3）面间裂缝和空洞检测：这类缺陷是由于计算误差或面片丢失造成的。对于裂缝和空洞，首先他们的边都是悬边。根据前文可以从悬边缺陷中得到，其中，空洞是首尾相连构成的一个环。用模型中所有的悬边构造一个无向图，通过无向图的广度优先遍历，可以得到顶点序列，然后再找出属于空洞的边，悬边数组中去除空洞边就是裂缝边了。

3 拟合几何特征

3.1 几何特征数据点的提取

提取属于某个特征的数据点的总体思路是：先获得一个属于该几何特征的三角面片，然后遍历这个三角面片的相邻三角面片，从中找到同样属于该几何特征的三角面片，依次递归寻找该三角面片的相邻三角面片中属于当前几何特征的三角面片，直到找到所有的三角面片。然后从找到的所有三角面片提取出不重复的所有数据点。即是所有属于当前几何特征的数据点。

1）棱边要素数据点的提取。如图4是STL模型中两个平面相交形成的棱边，图4(a)是STL模型渲染图，图4(b)是STL模型示意图，图4(c)是理想平面要素。本文以图4(b)中所示的一组相邻的三角面片作为棱边要素，棱边要素的数据点是这些三角面片所包含的不重复的点。图4(c)中要提取的数据点属于平面F1、F2相交形成棱边，、分别是这两个平面的法向量，朝向几何体外侧。要提取的三角面片需要满足以下两个条件：

（2）三角面片在棱边法向量上的投影在棱边的起点终点之间。

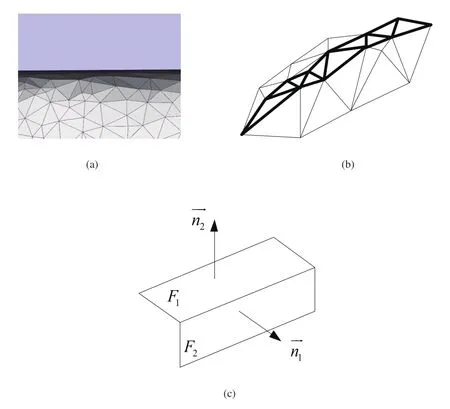
图4 STL模型中的棱边

2）平面要素数据点的提取。按照前面介绍的思路，第一步先从红黑树中提取一个属于平面要素的数据点。找第一个数据点的方法是先在理论模型中取理想平面上一点，再在STL模型中找与之距离最近的三角面片。之所以找最近的三角面片，不直接找最近的点是因为在STL模型中三角片的数量远远少于顶点的数量。在理想模型中取点时一般取平面中心的点，这样可以保证在STL模型中与之最近的点同样属于该平面。下一步是从面红黑树中读取三角面片的相邻三角面片，并判断相邻三角面片是否属于该平面。相邻三角面片满足以下条件的可以认为属于该平面：

（1）把理想平面边界和三角面片投影到坐标面内，该三角面片在该平面内的投影在平面边界投影的范围内；

（2）该三角面的法向量与理想平面的法向量成小角度。

如图4所示，t1和t2是两个三角面片，t1'和t2'分别是它们在坐标平面的投影，一个在平面边界投影范围内，另一个在平面边界投影的范围外，应用条件一可知t1属于该理想平面，t2不属于该理想平面。在选择投影坐标平面时，遵循使平面投影的面积最大原则。平面法向量那个方向的分量绝对值最大，说明垂直该分量的坐标面即为所选坐标面。

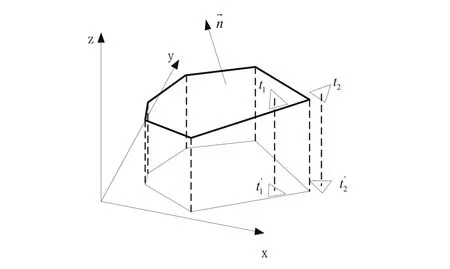
图5 平面在坐标面内的投影

3）圆柱面要素数据点的提取。提取圆柱面要素的数据点同样是先提取属于当前圆面要素的三角面片，然后从中找出所有不重复的点。凡是属于圆柱面的三角面片需要满足以下三个条件：

（1）三角面片到理想圆柱面轴线的距离近似为理想圆柱面的半径；

（2）三角面片的法向量与理想圆柱轴线夹角近似等于90°；

（3）三角面片应当位于理想圆柱面上下底面之间。

3.2 几何特征的拟合

拟合几何特征的过程可以看做是求解方程组的过程：加入某个几何特征上的点都满足f（p，x）=0，其中x是未知变量，x=（x1，x2，…，xn）T∈Rn，p是测量点，p=（px，py，pz）T∈R3。代入m个测量点后得到一系列方程组：

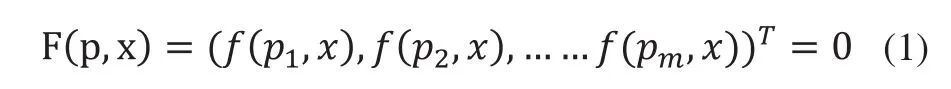
在用最小二乘法拟合特征时，该方程组是非线性方程组，解非线性方程组的方法有牛顿法[44]、高斯牛顿法、Levenberg-Marquardt（L-M）法，其中应用最广的还是L-M法。L-M法，中文名称列文伯格-马夸尔特法，是对高斯牛顿法的一种修正，加快了收敛速度[45]。使用LM法进行最小二乘寻优，关键是适当目标函数和合适的初始值。

1）空间直线的拟合。空间直线的点向式方程如下，其中点P0（x0，y0，z0）是直线上任意一点，向量（m，n，p）是直线的单位法向量：

那么点（x，y，z）到该直线的距离为：

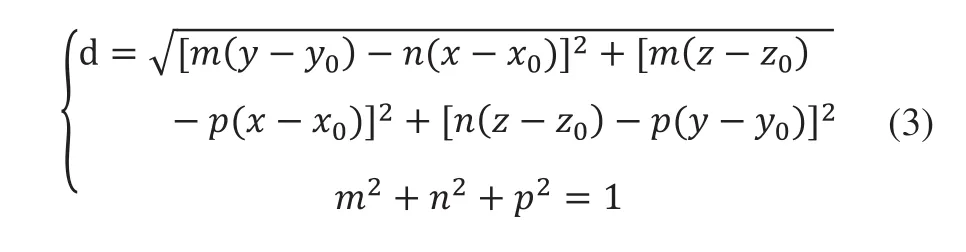
给定一组N个数据点{（xi，yi，zi），i=1，2，…，N}，优化目标函数为：

变量共有5个：x0、y0、z0、m、n，式中p用代替。拟合结果获得直线上一点的坐标和直线单位法向量。

2）平面拟合。用平面上一点P0（x0，y0，z0）和平面的单位法向量（m，n，p）来表示任意平面，若P（x，y，z）是平面上任意点，那么垂直：

那么点P（x，y，z）到该平面的距离为：

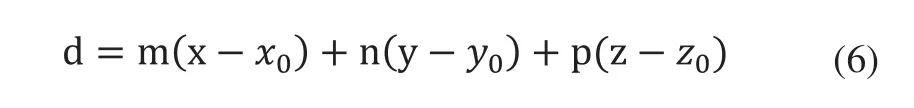
给定一组N个数据点{（xi，yi，zi），i=1，2，…，N}，优化目标函数为：

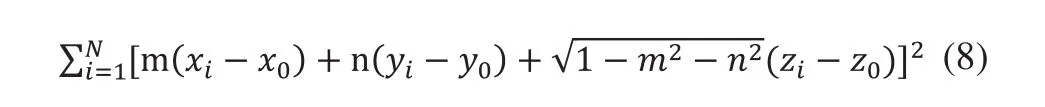
变量共有5个：x0、y0、z0、m、n。拟合结果获得平面上一点的坐标和平面的单位法向量。

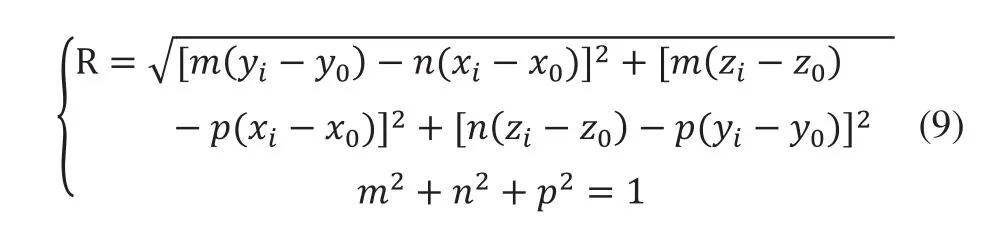
给定一组N个数据点{(xi，yi，zi)，i=1，2，…，N}，优化目标函数为：

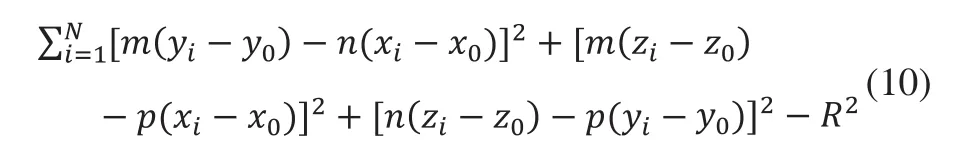
变量共有6个：x0、y0、z0、m、n、R，式中p用代替。拟合结果获得圆柱中心轴线上一点的坐标和轴线的单位法向量。

3.3 公差的计算

在计算多几何要素公差的某些公差项目，比如线性尺寸公差的定义是两个提取平面的局部尺寸，在计算局部尺寸时需用到拟合导出中心平面，而拟合导出中心平面按照定义是两个平行的拟合组成平面的中心平面，虽然这两个平面的理想平面是平行的，但实际上两个组成平面的拟合平面不一定平行，我们还是用平面上一点和平面的单位法向量来描述一个平面，那么在两个拟合提取平面上各取一点，它们的中点在拟合导出中心平面上，法向量为两个拟合提取平面法向量的角平分线方向的向量。图6是计算拟合导出平面的过程。平面F1、F2是两个提取组成平面，F3是要求的拟合导出中心面。点p1、p1分别是拟合组成平面F1、F2上一点，向量、分别是F1、F2的法向量。点p3是点p1、p1中点，向量是、的角平分线。拟合导出中心面F3由点p3、单位向量来描述。

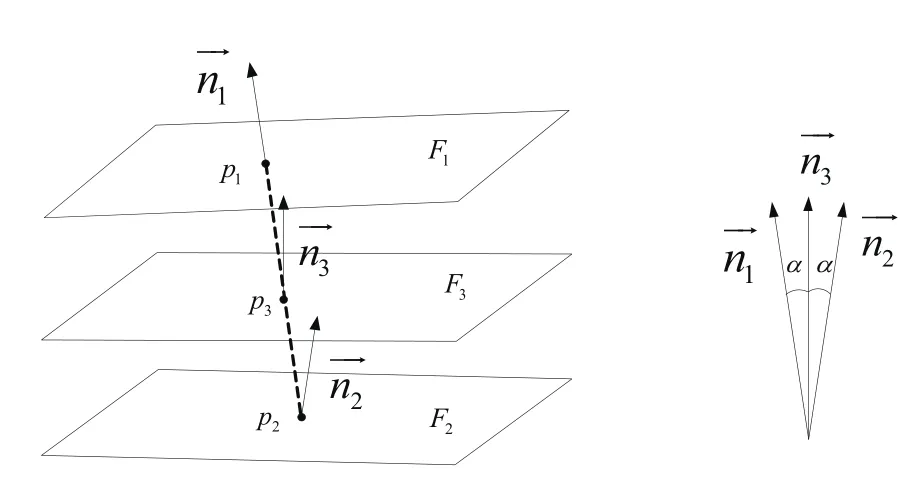
图6 拟合导出平面

在计算含有基准的公差项目时，基准的位置应当是几何要素的理想位置，但是由测量得到数据点无法知道理想位置，因此用拟合得到的几何要素作为理想几何要素。

在计算公差时需要大量计算空间直线与三角面片集合（或者点云）的交点，比如求点到提取平面的距离，求两平面间距离时的局部尺寸等等。计算直线与三角面片集合（点云）的方法有很多种，本文采取的方法如图7所示，已知拟合平面F，空间直线L，交点为P，在平面的点云数据中搜索找到离点P最近的三个点p1、p2、p3，这三个点可以组成一个三角面片，三角面片的中点是p'，p'即是直线L与平面的实际交点。

图7 直线与平面交点

求点p的过程如下，已知平面F上一个点P1（P1x，P1y，P1z），法向量为（n1x，n1y，n1z），直线上一点P2（P2x，P2y，P2z），法向量（n2x，n2y，n2z）。直线的参数方程为：

平面的点法式方程为：

解上面三个方程得到：

把t代入直线方程得到交点坐标。

4 STL模型可视化

STL数据模型可视化的实现是在线服务以及加工中的一个重要环节。模型可视化功能的实现有助于对STL文件进行诊断，良好的模型显示效果对客户的直观感受及正确的选择实体的切片方向有积极的效果。本次设计充分利用Three.js卓越的渲染能力和交互使场景处理能力，在WEB前端实现STL数据模型的可视化。如图8是加载完成的STL模型。

图8 加载完成的STL模型文件

Three.js为用于3D场景渲染的Java Script开源库，并且由于其具有极强兼容性，支持加载多种式的文件，所以以Three.js引擎作为工具对STL模型进行加载和渲染。Three.js库中包含许多个工具文件，每一个文件中都封装着完成特定功能的方法。Three.js文件是Three.js引擎中使用频率最高的工具文件，其中封装了调整场景、摄像机和材质的相关方法，可以方便快捷地对渲染场景进行初始化。Three.js引擎发展至今已经有了多种加载器，可以支持JSON、OBJ、STL、CTM等多种格式。

图9 引入JavaScript文件

使用Three.js引擎对STL模型进行读取之前，首先要引入必要的JavaScript文件，如图9所示，STLLoader.js是STL文件对应的加载器文件，文件中封装了读取STL二进制文件和STL文本文件数据并初始化网格体的方法；TrackballControls.js是控制模型视角变换的函数库文件；AsciiEffect.js是添加ASCII动画效果的js文件。

如图10所示，依次通过初始化渲染场景（设置相机位置、光源位置及属性等）、加载STL文件、渲染计算等步骤实现STL模型的可视化。其中scene是一个场景容器，用来跟踪并保存所有需要渲染的物体。

图10 初始化流程

5 结果与探讨

本例所用的机器采用先临三维科技公司自主研发的Shining3D-Scanner系列三维扫描仪。使用激光扫描仪扫描打印好的组件得到STL模型，本例中命名为model.stl。使用STL模型解析算法和错误检测算法对模型进行分析，得到的模型信息结果和错误信息结果如图11所示。其中的反向面片、壳体和岛孔错误使用Magics软件处理，由于微小面片对本例分析不会造成影响，故不考虑该问题。

图11 模型信息和错误信息

本例选取了尺寸公差、平行度公差、平面度公差作为特征拟合的检测项目。如图12所示为几何精度参数检测界面和检测结果。使用PMI标注功能，将检测结果直接标注在三维零件上。其中绿色标注代表符合公差要求，红色标注代表超出公差要求范围。

图12 几何精度参数检测结果

6 结论

近年来3D打印技术受到了广泛的关注，但是在3D打印技术缺乏有效的数字化质量表征技术，严重阻碍了3D打印技术的推广应用。本文针对该问题系统研究了基于STL模型的数字化模型数据分析、质量表征参数，从几何精度、表面质量和其他质量参数三个方面进行了深入研究，为产品质量数字化检测提供了新的思路。