互耦条件下MIMO雷达非圆目标稳健角度估计方法

王咸鹏，国月皓，黄梦醒，沈重，曹春杰，冯文龙

（1. 海南大学南海海洋资源利用国家重点实验室，海南 海口 570228；2. 海南大学信息与科学技术学院，海南 海口 570228)

1 引言

多输入多输出（MIMO, multiple input multiple output）雷达概念一经提出，就立即引起了雷达研究领域学者们的广泛关注[1-2]。由于 MIMO雷达发射的是正交波形，采用发射天线与接收天线分置的方式获得波形分集与空域分集，因此与传统的雷达相比，MIMO雷达具有更好的识别性能和参数估计性能，特别是对于联合角度的离开方向（DoD,direction-of-departure）与到达方向（DoA, direction-of-arrival）估计[3-4]。

在双基地的MIMO雷达中，联合DoD与DoA估计是一个热门课题[5]，针对该课题，学者们提出了许多有效的算法，例如多重信号分类（MUSIC,multiple signal classification）算法[6]、旋转不变子空间（ESPRIT, estimation method of signal parameter via rotational invariance technique）算法[7]，以及其他的一些子空间算法[8-9]，但这些算法依赖于理想的收发阵列模型。由于收发阵元往往不能够精确补偿，导致阵元间存在互耦的情况[10-11]。针对这一情况，主要的解决办法有MUSIC-like和ESPRIT-like等方法[12-13]。其中，ESPRIT-like算法应用均匀线阵中互耦矩阵的带状对称Toeplitz结构来消除互耦的影响，但以损失阵列孔径为代价。以上提出的方案并没有考虑信号的非圆特性，针对信号的非圆特性，文献[14]研究了一种在互耦情况下的DoA估计方法，该算法在考虑了信号非圆特性的同时消除了互耦的影响，且利用非圆结构信息补偿了部分阵列孔径的损失。另一方面，在互耦的条件下，针对信号的多维结构特性，学者们也进行了部分的研究工作[15-16]，文献[15]介绍了基于酉张量分解的子空间估计方法，该算法在消除互耦影响的同时，将张量子空间通过酉变换转换为实值张量，接着利用张量的多维结构进行角度估计，不仅提高了识别性能，还降低了运算复杂度。以上这些算法都是单独利用信号的非圆特性或多维结构特性，不能在补偿部分阵列孔径的损失的同时提高算法的角度估计性能。

本文提出了一种互耦条件下 MIMO雷达的稳健DoD和DoA联合估计算法，既利用信号本身的多维结构，同时也考虑信号的非圆特征，扩大了阵列孔径，获得了更加精确的识别性能。所提算法利用互耦矩阵带状对称的Toeplitz结构来消除未知互耦的影响，因此能够在互耦的情况下对非圆目标进行准确的角度估计，比其他方法具有更好的识别性能。同时为了减少运算复杂度，所提算法利用张量的酉变换，将子空间张量转化为实值张量，大大提升了算法的运算速度。仿真结果表明，所提算法具有有效性与优越性。

2 张量基础与信号模型

2.1 张量基础

本节主要阐述了张量的基础知识与定义，更多相关知识可以从文献[17-18]中得到。

本节主要阐述了张量的基础知识与定义，更多相关知识可以从文献[17-18]中得到。

定义1 模式-n矩阵展开。设张量张量X的模式-n矩阵展开定义为的元素对应的元素，其中

定义2 模式-n矩阵积。张量与矩阵的模式-n积定义为其中

此外，模式-n矩阵积满足以下性质

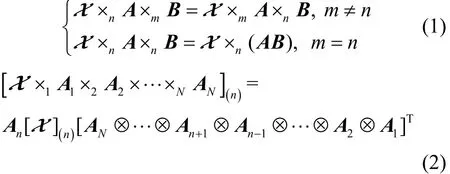
其中，⊗为Kronecker积。

定义3 张量分解。张量X∈ℂI1×I2×…×IN的高阶奇异值分解定义为

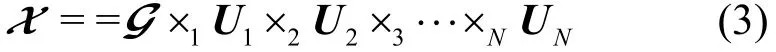
定义4 张量模式-n串联。张量X∈ℂI1×I2×…×IN与张量Y∈ℂI1×I2×…×IN的模式-n串联定义为其中

2.2 信号模型

考虑一个窄带双基地MIMO雷达，它由M个发射阵元与N个接收阵元构成，两者都是半波长的均匀线性阵列（ULA, uniform linear array），M个发射阵元发射M个相互正交的非圆信号。假设在远场有K个相互独立的目标，对于发射阵列与接收阵列，第K个目标的发射角和接收角分别为ϕk和θk。那么接收端接收到的信号可表示为

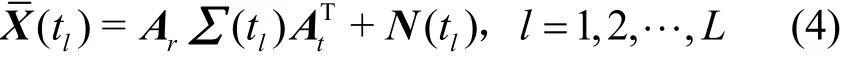
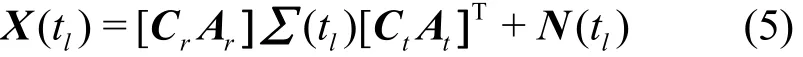
其中，C=Toeplitz([cT,0])∈ℂM×M和

tt1×(M-P-1)为互耦矩阵，其中ct= [ct0,ct1,⋅⋅⋅,ctP]，cr= [cr0,cr1,⋅⋅⋅,crP]。cip(i=r,t;p= 0 ,1,2,⋅⋅⋅,P)是P+1个非零互耦系数，满足 0 ＜|cip|＜⋅⋅⋅＜|ci1|＜|ci0|= 1。

根据模式-n矩阵展开的定义，式(5)中接收到的数据矩阵可以看作沿第三维脉冲方向的切片，然后将矩阵X(tl)的数据在第三维上堆叠，便得到N×M×L维的张量X。根据模式-n矩阵展开的定义，可以把张量X改为

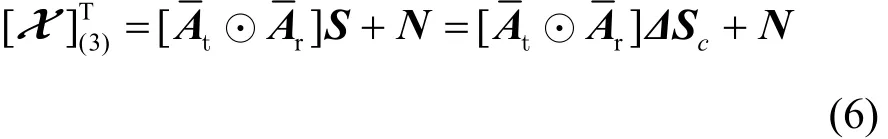
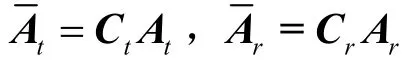
其中，⊙为Khatri-Rao积；为发射与接收导向矩阵；为信号矩阵；满 足

3 基于酉张量分解的稳健角度估计算法

3.1 互耦消除

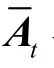
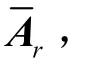
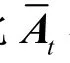
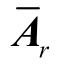
由于收发阵元间的互耦效应影响了发射矩阵与接收矩阵因此与不再是范德蒙矩阵。同时注意到互耦矩阵为带状对称Toeplitz矩阵，于是从发射与接收矩阵提取出 2个子矩阵用来去耦。故2个选择矩阵可定义为

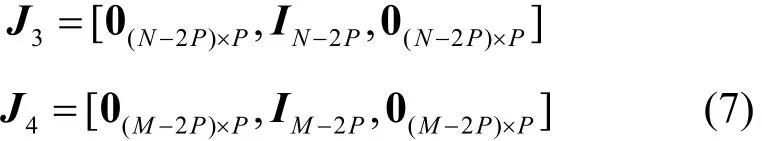
根据互耦矩阵的特点，则有

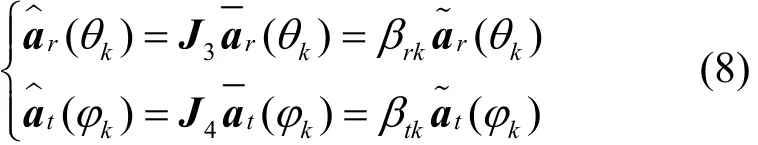
为了能够在张量域中体现去互耦的过程，式(8)在张量域的扩展可表示为

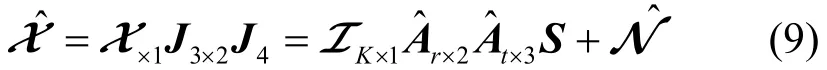
根据模式-n矩阵展开的定义，模式-3的矩阵展开可以写为

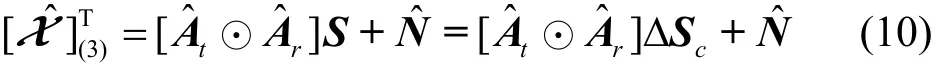
3.2 增广矩阵与信号子空间估计

为了在张量域中同时利用信号的非圆性，通过前后向平滑技术构造了一个特殊的增广张量

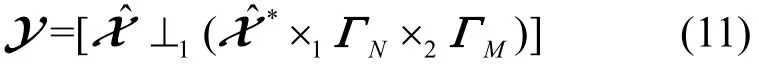
其中，（⋅）∗为共轭运算，ΓK代表次对角线处元素为1、其他元素为0的矩阵。根据模式-n矩阵展开的定义，Y∈ ℂ2N~×M~×L模式-3的矩阵展开可以写为

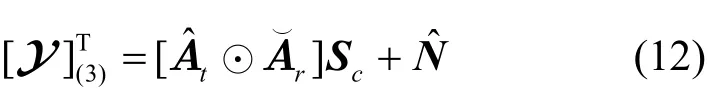
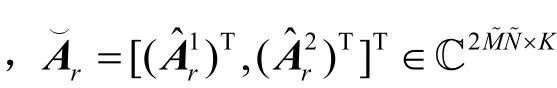
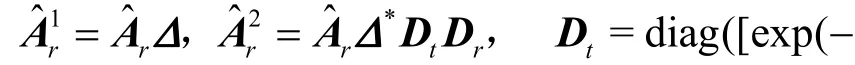
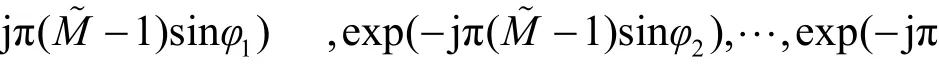
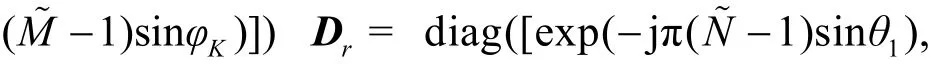
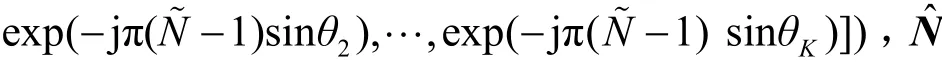
其中表示扩展导向矩阵 ，为噪声矩阵。从式(12)可以看出，此时的阵列孔径为式(10)的2倍。由此可以得知，增广张量Y不仅考虑到了张量的多维结构，还捕捉到了信号的非圆性，扩大了阵列的虚拟孔径，从而获得更加优越的参数估计性能。

由于式(11)使用了前后向平滑技术，因此张量Y在张量域具有centro-Hermitian特性，于是利用酉变换将式(11)转换为实值张量[19]

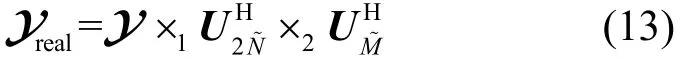
其中，( ⋅)H为共轭转置运算，U2K+1为酉矩阵，定义为

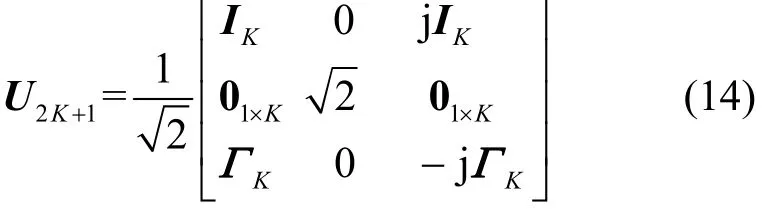
把U2K+1中间一行与中间一列删去便得到U2K。对式(13)使用高阶奇异值分解得到[20]

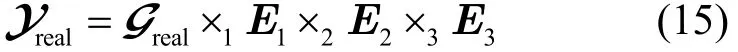
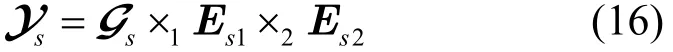
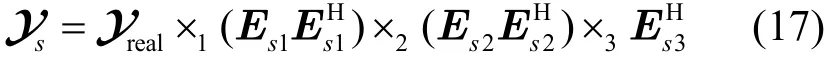
根据模式积的性质，有

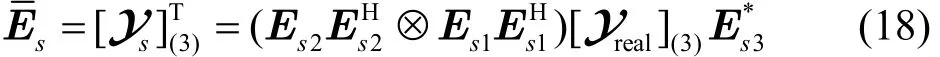
根据文献[15]中的定义，将式(18)简化为

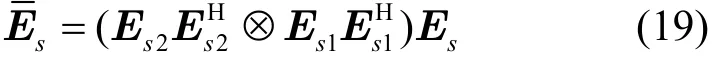
3.3 联合DoD与DoA估计

为了得到DoD与DoA估计，利用以下旋转不变性方程[21]

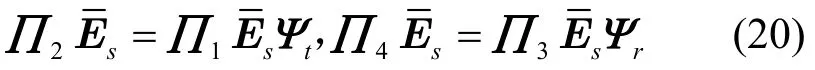
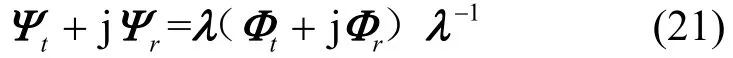
其中，（⋅）-1为逆运算。从Ψt+jΨr的特征值的实部和虚部能分别得到对角矩阵Φt与Φr。紧接着DoD与DoA便能自动匹配，DoD与DoA通过以下计算式获得

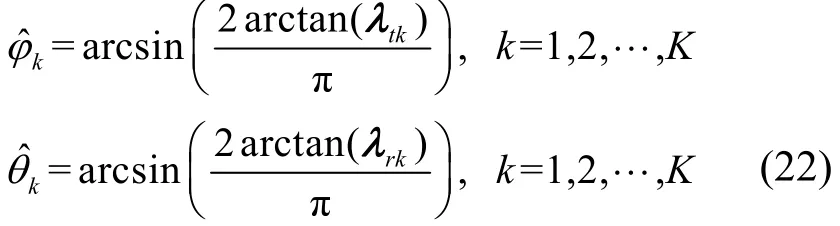
其中，λtk与λrk分别是Φt与Φr的第k个对角元素。

3.4 运算复杂度分析

根据文献[23]可知，对于一个M×N维的矩阵，对其进行K秩截断奇异值分解（SVD, singular value decomposition），需要的运算复杂度为O(MNK)。另一方面，由于实值运算的复杂度为复值运算的且所提算法的运算量大部分聚集在对于实值张量Yreal的高阶奇异值分解，即对张量Yreal使用三维SVD，因此相应的运算复杂度为文献[15]中的Tensor unitary ESPRIT算法需要的运算复杂度为若直接对式(11)中的复值张量Y使用SVD，则相应的运算复杂度为因此所提算法通过酉变换进行实值运算较大程度地减少了相应的运算复杂度。尽管 Tensor unitary ESPRIT也是实值分解的算法，但所提算法的虚拟孔径为Tensor unitary ESPRIT算法的2倍，因此后者的运算量为前者的2倍。

4 仿真结果

本文将所提算法与ESPRIT-like算法[13]、Tensor unitary ESPRIT算法[15]和克拉美罗界（CRB,Cramer-Rao bound）[13]进行比较，通过仿真实验证明本文所提算法的优越性。在仿真中，双基地MIMO雷达拥有M=8个发射天线，N=10个接收天线，除非另有说明，设定目标数目为K=3，这3个目标分别位于(φ,θ) = (-10o,10o)、

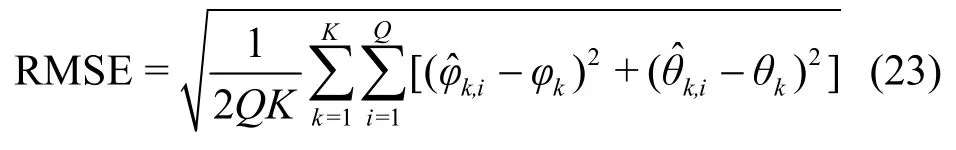
11(φ2,θ2)=(-8o, 8o)和 (φ3,θ3) = (15o,-15o)。仿真结果采用均方根误差（RMSE, root mean square error）进行角度估计性能评估，定义为其中，φˆk,i、θˆk,i分别是 DoD 的φk和 DoA 的θk在第i次蒙特卡罗实验的估计结果，Q是蒙特卡罗实验的总数，本文中Q=500。另一个用来评价角度估计性能的参数为成功检测的概率（PSD, the probability of the successful detection），定义为

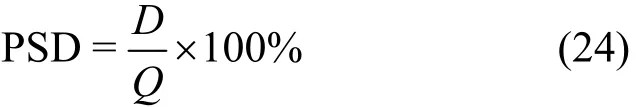
其中，D为正确识别的总次数，而正确的实验要求所有估计角度的绝对误差小于在仿真中，设置互耦参数为ct= [ 1,0.2 +j0.061]，cr=[1,0.15+j0.0251]，这些参数意味着在接收阵列与发射阵列中，前2个天线的位置较近，存在互相耦合的影响。

图 1对比了在 3个目标时不同算法中 SNR对RMSE的影响，快拍数设置为L=100。从图1可以看出，在整个信噪比区间中，本文所提算法的角度估计性能优于Tensor unitary ESPRIT算法与ESPRIT-like算法，且靠近CRB。这是因为本文所提算法不仅利用了信号的多维结构，而且还考虑到了信号的非圆特性，而其他算法仅仅考虑了非圆结构特性或张量结构特性。仅次于本文所提算法的是 Tensor unitary ESPRIT算法，它的性能优于ESPRIT-like算法，这是因为Tensor unitary ESPRIT算法考虑到了信号的多维结构，在存在互耦的条件下获得了优良的识别性能。

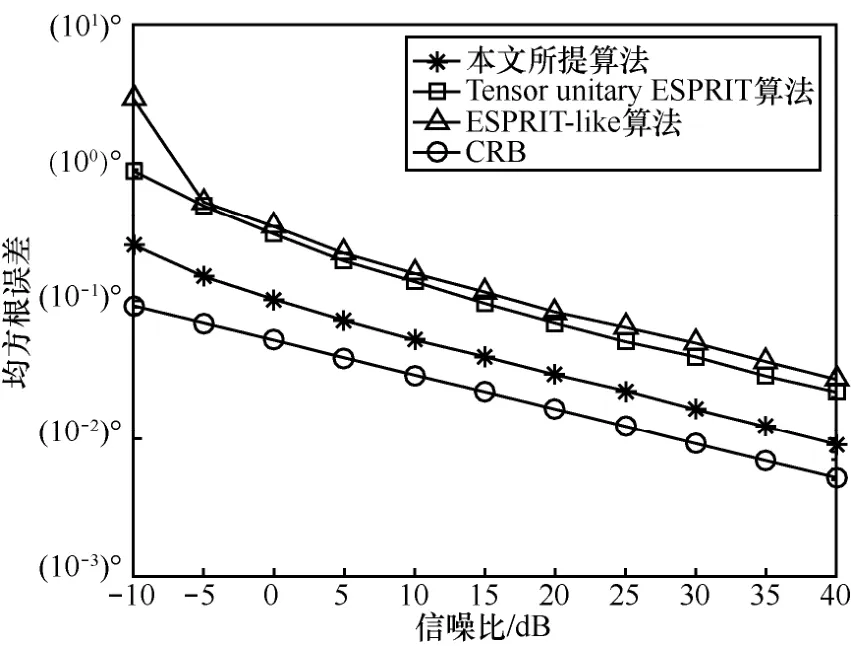
图1 RMSE与SNR的关系（3个目标）

图 2对比了在 2个目标的情况下不同方法的SNR对 RMSE的影响，这 2个目标分别位于快拍数设置为L=100。从图2中可以看出，本文所提算法的性能依旧优于Tensor unitary ESPRIT算法与ESPRIT-like算法。另外，Tensor unitary ESPRIT算法的识别性能依旧优于ESPRIT-like算法。

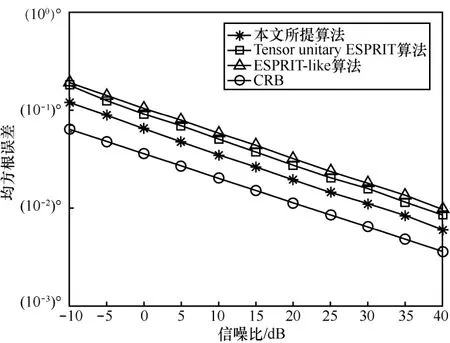
图2 RMSE与SNR的关系（2个目标）

图3描述了快拍数的变化对RMSE的影响，其中SNR=0 dB。从图3可以发现，随着快拍数的增长，所有算法的性能都得到了不同程度的提高，且本文所提算法的总体性能优于 Tensor unitary ESPRIT算法与ESPRIT-like算法。在非常低的快拍数下，Tensor unitary ESPRIT算法的性能优于本文所提算方法，这是由于Tensor unitary ESPRIT算法通过空间平滑有效地增加了快拍数。当快拍数大于50个时，本文所提算法性能优于Tensor unitary ESPRIT算法与ESPRIT-like算法，与CRB十分接近。另外，在大快拍数的条件下，Tensor unitary ESPRIT算法的性能与 ESPRIT-like算法的性能接近一致，但是仍然劣于本文所提算法。

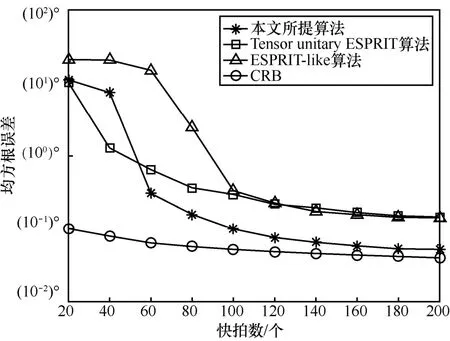
图3 RMSE与快拍数的关系

图4描述了几种方法的识别成功率与SNR之间的关系，快拍数设置为L=50。从图4可以看出，所有的算法在SNR足够高时，都能够达到100%的识别成功率，但是本文所提算法的识别成功率能够更快地达到100%。在SNR相同的情况下，本文所提算法比其他算法拥有更高的识别成功率。一方面，本文所提算法能够同时合理地利用信号的非圆特性和多维结构特性，提升角度估计性能；另一方面，本文所提算法只涉及实值运算，有效地减少了运算复杂度。

5 结束语

本文针对 MIMO雷达中存在未知互耦的非圆信号，提出了一种基于酉张量分解的角度估计算法。所提算法构造了一个特殊的增广张量用来捕获非圆信号的非圆特性与多维结构，且可以在张量域中消除互相耦合带来的影响。另外，所提算法通过酉变换将数据转化为实值，极大地降低了运算复杂度，节约了运算时间。通过分析得知，所提算法比现有的基于子空间的识别算法拥有更好的识别性能，特别是在低信噪比和低快拍数的条件下。仿真结果表明，本文所提算法在识别性能上具有优良性。

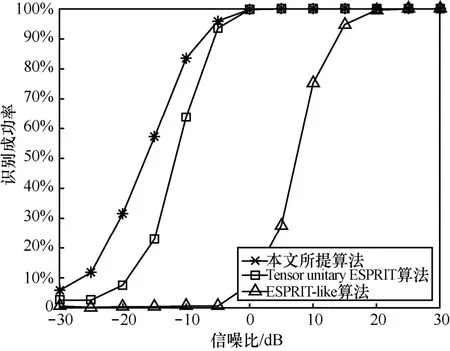
图4 识别成功率与SNR的关系