立足忘“形”得“一” 实现由“厚”到“薄”*
●刘鑫钧 高 娇
(灌南高级中学,江苏 灌南 222500)
道生一,一生二,二生三,三生万物.学习的关键在于领悟“道”,而要领悟“道”就需先得“一”,这个“一”应该是简单的、也是最本质的.然而在高三复习教学中,学生往往被厚厚的书本、沉甸甸的试卷压得喘不过气来,教师不断重复、拉网式的讲题,只见厚的教学,却未见教学的薄,使得学生只见“万物”而未得一.
如何得“一”呢?这就需要忘“形”.而这之前需要经历3个过程,即展“形”、变“形”与析“形”,通过这3个过程对相关联的或类似的概念、问题、认识等作横向、纵向沟通,并力求在“越界而读”上下足功夫,即将所学知识读厚,接下来需要的就是读薄,忘却“外在的形”(即非本质的属性),只有这样心中才一片空明,才能吐故纳新、忘却形式、抽象本质,乃为得其“一”.本文基于笔者的教学经验,从3个方面来阐述在高三复习教学中如何忘“形”得“一”,实现教学的“厚”向教学的“薄”转化.
1 忘“形”得“一”,领悟概念之间的联系性
概念复习教学的一个重点就是让学生认识到概念之间具有一定的联系,而不是割裂地认识问题.在概念复习教学中,如何提高概念知识的联系性呢?
1.1 展“形”——呈现概念的形式化语言
案例1 “函数单调性”概念的复习教学.
符号语言的抽象性使得学生对概念理解存在一定的困难,因此,在复习教学时需要加强学生对概念形式化定义的进一步理解,以函数单调性概念为例,在高三复习时可以让学生回顾、表述概念的形式化定义.
问题1 什么是单调递增函数?它是如何定义的?
生:一般地,设函数y=f(x)的定义域为A,区间I⊆A.如果对于区间I内的任意两个值x1,x2,当x1 教师可以向学生依次提出以下4个问题,通过不断变化定义的形式,让学生真正感悟概念形式化定义的本质. 问题2 把“f(x1) 问题3 把“f(x1) 上面这些形式各有不同,如何把握它们的联系与区别,将学生对概念的本质认识不断引向深处呢?可以向学生追问以下5个问题. 问题6 单调性实质上就是考查f(x2)-f(x1)与x2-x1之间的什么关系? 问题7 (x2-x1)[f(x2)-f(x1)]>0;当x1 问题9 若A(x1,f(x1)),B(x2,f(x2))为函数y=f(x)图像上的两个点,那么函数f(x)在[x1,x2]上的平均变化率是什么?与单调性有什么关系? 问题10 “函数在区间A上的单调性”与其导数f′(x)有何关系呢? 高三解题教学贵在跳出题海,掌握基本的解题经验,使学生获得一类试题的通法通性,不被试题“外在之形”所迷惑,于四面题海之中获“试题之本意”,从纷繁复杂之中跳出来,游刃而有余.那么,在解题教学中如何忘“形”得“一”,才能让学生掌握一类试题的普适性解法呢? 案例2 直线与圆的一类比例问题的解题教学. 《普通高中数学课程标准(2017年版)》强调:对学生“直观想象”这一数学核心素养的培养,指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,培养理解和解决数学问题的素养.因此,在解题教学中要鼓励学生把试题中元素的位置、形态用图形语言表示出来.从哪入手呢?波利亚指出:从最简单的开始. 例1 过点P(-4,0)的直线l与⊙C:(x-1)2+y2=5相交于点A,B,若点A恰好是线段PB的中点,则直线l的方程为______. 图1 该题的图形表征大致如图1所示.在表征的过程中认识到:只有当直线l处于一个特定位置时,点A才可能恰好是线段PB的中点.在画图的过程中,发现学生画图的顺序有所不同,有的学生是先画直线,后标注点A,B,即先产生直线,因此可以先假设直线斜率k,然后求点;有的学生先画点,再联结两点所在直线,最后出现另一点,这样就可以设点来做.利用几何图形描述问题,借助几何直观理解问题,在图形表征过程中实现了动态地理解问题. 解题教学不仅要一题多解,更要善于多题一解,因此要善于对问题进行变式.顾泠沅等学者把变式教学分为概念性变式教学和过程性变式教学两类.概念性变式教学突出对概念内涵的理解,过程性变式教学突出对概念外延的应用,注重知识之间的联系和拓展,通过过程性变式教学,使数学教学有层次地递进[1].利用过程性变式可以对一个初始问题进行变式,从而深化对这类问题的认识. 2.2.1 改变元素 变式1 (定点变动点)过点E(2,t)作直线l与⊙C:x2+y2=1交于点M,N,若点M恰好是线段NE的中点,则实数t的取值范围是______. 变式2 (竖线变斜线)已知⊙C:(x-2)2+y2=1,点P在直线l:x+y+1=0上,若过点P存在直线m与⊙C交于点A,B,且点A为PB的中点,则点P横坐标x0的取值范围是______. 变式3 (定圆变动圆)已知△ABC的3个顶点A(-1,0),B(1,0),C(3,2),其外接圆为⊙H. 1)略. 2)对于线段BH上的任意一点P,若在以C为圆心的圆上都存在两个不同的点M,N,使得点M是线段PN的中点,求⊙C的半径r的取值范围. 图2 2.2.2 变更条件 变式4 (中点变向量)如图2,在平面直角坐标系xOy中,已知⊙M:x2+y2-12x-14y+60=0及其上一点A(2,4). 1),2)略. 变式5 (直线变动圆,中点变比例)在平面直角坐标系xOy中,⊙C1:(x+1)2+(y-6)2=25,⊙C2:(x-17)2+(y-30)2=r2.若⊙C2上存在一点P,使得过点P可作一条射线与⊙C1依次交于点A,B,满足PA=2AB,则半径r的取值范围是______. 图3 例1及5个变式的图形表征如图3所示,下面需要整合这6个图形,即把一些零散的东西通过某种方式而彼此衔接,其主要的精髓在于将零散的要素组合在一起,并最终形成有价值、有效率的整体. 首先,可以看出从例1到变式1是定点变动点,变式2中的直线可以是横线(x轴)、竖线或斜线,其中线段比例关系为1∶1,圆始终是定圆.因此,这3个图形可以整合为下列一个基本的模型. 模型1 过直线l上一点P作一条直线,交定圆于点A,B,其中PA∶AB=1∶1. 在高三的解题教学之中,如果就题讲题,那么教师、学生都将陷于题海之中而不能自拔,如何得其“一”,而忘其形呢?关键的一步就是要对题型、解法归一. 2.4.1 题型的概括抽象 2.4.2 解法的提炼与统一 通过以上分析发现这6道题本质上是一类题型,因此,在教学的过程中应引导学生掌握这一类题型普适性的解法,而不是一题一题进行讲解.为便于具体说明,这里以曲线C是直线或圆、C1是⊙H:(x-a)2+(y-b)2=r2为例. 利用点B在⊙H上,得方程 整理变形,得 (1) 然后利用点A在⊙H上,获得方程 (x1-a)2+(y1-b)2=r2. (2) 数学教学重在培养学生的思维,而思维的水平又有高低之分.在高中数学课堂教学中,要善于引导学生对问题进行深刻理解.深刻性指思维活动的抽象性和逻辑推理水平,表现为能深刻分析、理解问题,善于抓住事物的本质和规律.具体表现在3个维度:宽度、深度和完整度.那么,在解题教学中如何忘“形”得“一”,才能让学生对问题有深刻性的理解呢? 案例3 运用韦达定理求直线与椭圆交点坐标. 直线与椭圆的位置关系有3类:相离、相切、相交.当直线与椭圆相交时,如何求直线与椭圆的交点坐标呢?理论上直接联立直线方程与椭圆方程,得方程组 消去x(或y)得到关于y(或x)的方程,解这个方程即可.如果知道一个交点的坐标,利用韦达定理和或积的形式会更加简便,因此,运用韦达定理求直线与椭圆的交点问题主要是针对直线与椭圆相交、且已知其中一点坐标这一类模型.用图形表征如图4所示. 图4 图5 2)若x0=0,求椭圆的离心率; (2015年江苏省南通市第二次模拟试题第18题) 分析 由于点P(x0,y0)满足PA⊥PF,从而 化简,得 (3) 因为点P(x0,y0)在椭圆上,所以 (4) 联立式(3)和式(4),得 (5) 于是 因此 图6 图7 分析 例3中求点P的横坐标与例2的解法是一致的,同样可得到关于xP的一个一元二次方程,然后要看出a是方程的根.利用韦达定理求出xP,最后利用xP∈(-a,a)求出离心率的范围. 通过对图5和图6分析发现,韦达定理适用于这样一类模型,这一类模型具有更一般的特征:如果动点P与定点A(a,b)在椭圆上,Q(m,0),其中m为常数,且PA⊥QA,如图7所示. 图8 1)求椭圆C的方程. 2)是否存在常数λ,使得k1=λk恒成立?若存在,求出λ的值;若不存在,请说明理由. 2)判断常数λ是否存在的关键是求出k1,k2,因此问题的关键在于如何求解k1(求解k2同理可得),即点A1,B1的坐标如何求解,但点A1,B1都是动点,不属于前两类模型,怎么办?受图4的启发,可以先设A(x0,y0),暂时把x0看成常数,首先求出直线AM的方程 因为该方程有两个根x0,xA1,所以 化简得 则 同理可得 下略. 对图4~8进行分析可知:运用韦达定理求直线与椭圆交点具有广泛性,其中图7所代表的题型是对图5与图6所代表的题型的一般性概括.这些图形大致可以分为3类:第一类如图4所示,过椭圆上一定点作直线l交椭圆于另一点,求另一点坐标;第二类如图7所示,已知椭圆上动点P与定点A(a,b),定点Q(m,0)不在椭圆上,且PA⊥QA,求动点P坐标;第三类如图8所示,已知椭圆上双动点,求动点坐标. 通过前面的展“形”、变“形”、析“形”,对运用韦达定理求直线交点这一问题有比较深入的认识.试题的形式千变万化,因此需忘却形式,获得本质的认识,才能灵活地运用韦达定理去解题.虽然形式上有3类题型,但是本质上就一种,就是最后获得关于坐标的一元二次方程 (6) 展“形”只是第一境界:见山是山,见招是招.变“形”是第二境界:见山不是山,见招不是招,学生经过展“形”、变“形”,即不断读厚的过程,之后会发现,到处都是山到处都是招.下面就需要一个读薄的过程,这就需要析“形”与忘“形”,忘就是为了记,忘却形式,记住本质,方能得“一”.最后进入学习的第三境界:见画还是画,见招还是招,道法自然,一切从心.1.2 变“形”——基于问题串追问概念的形式化语言


1.3 析“形”——探究不同形式语言的区别与联系

1.4 得“一”——概括形式语言的本质与联系


2 忘“形”得“一”,掌握一类问题的普适性解法
2.1 展“形”——表征图形中元素位置形态

2.2 变“形”——变换图形中元素及位置关系


2.3 析“形”——整合相关图形




2.4 得“一”——对模型本质的概括与普适性解法的提炼



3 忘“形”得“一”,促进对问题的深刻性理解
3.1 展“形”——了解运用的宽度

3.2 变“形”——扩宽运用的深度






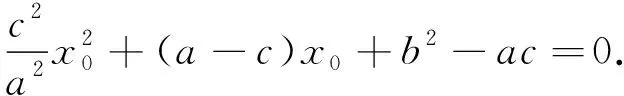





3.3 析“形”——建构定理运用的完备性认识
3.4 得“一”——掌握定理运用的本质


4 结束语

