对一道浙江省学考试题的思考*
●张 玮
(学军中学,浙江 杭州 310012)
2019年1月浙江省普通高中数学学业水平考试(下面简称学考),其中有一些题目很有意思,选择题的最后一题引起了笔者的兴趣.

图1
例1 如图1,线段AB是圆的直径,圆内一条动弦CD与AB交于点M,且MB=2AM=2,现将平面ACB沿直径AB翻折,则三棱锥C-ABD体积的最大值为
( )
(2019年1月浙江省普通高中数学学业水平考试第18题)
解 先固定CD,由于翻折后三棱锥的底面积是确定的,故只需求高h的最大值即可,即点C到平面ABD距离的最大值.设在翻折过程中MC和平面ABD所成的角为θ,由最小角定理可知
h=CMsinθ≤CMsin∠CMB,
即当面ACB⊥面ABD时,体积V最大,因此,
又
CM×DM=AM×BM=2,
从而
V≤sin2∠CMB≤1,
当CM⊥面ADB时,V=1.
评注 例1属于立体几何中的翻折问题.但是在求CM×DM的值时,需要用到平面几何中的相交弦定理,因此例1是平面几何和立体几何的一个完美结合.该题考查了立体几何线面角中的一个重要结论,有一定的思维量,难度适中,作为学考选择题的最后一道是最合适的.
翻折问题是高考立体几何中的常客,但是将平面几何和立体几何结合起来的翻折问题,为数不多.因此笔者对此题作了探究,并推广到解析几何.
1 变式
由于CD是动弦,因此沿CD对折,将更具变化性.由此得到了例2:

图2
例2 如图2,线段AB是⊙O的直径,圆内一条动弦CD与AB交于点M,且MB=2AM=2,现将平面BCD沿CD翻折,则三棱锥A-CBD体积V的最大值为______.
解 由例1的解答可知
过点O作ON⊥CD于点N,并设∠CMB=α,则
故
令f(x)=(9-x)x2,其中x∈(0,1],则
f′(x)=-3x2+18x,
从而y=f(x)在(0,1]上单调递增,于是
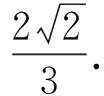
在例2的解答过程中,同样考查了线面角的重要结论,同时还考查了导数的简单应用,是一个不错的训练题.另外若将例1中的圆改成椭圆,则可以将结果推广到圆锥曲线中,而立体几何和解析几何的结合,也使得题目(如下面的例3)变得更加亮眼.
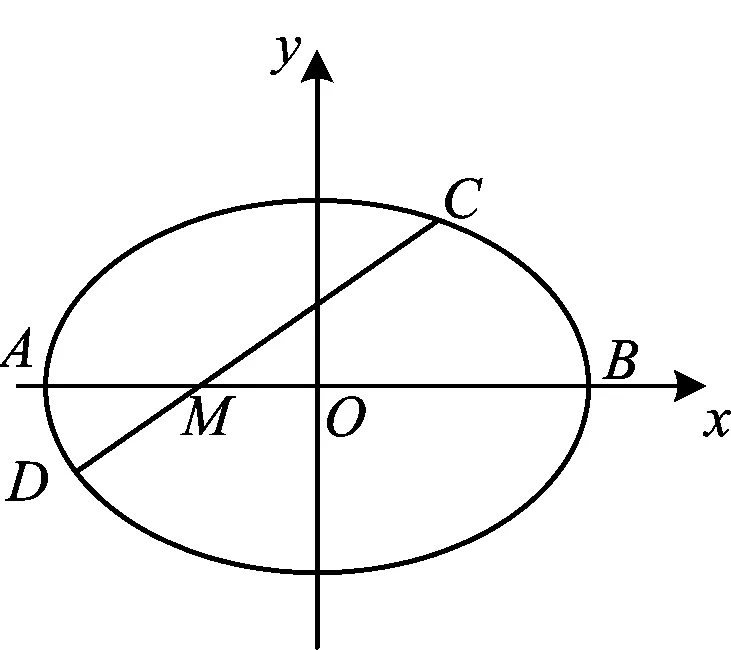
图3
2 推广

解 设定点M(r,0)(其中-a (b2m2+a2)y2+2b2mry+b2r2-b2a2=0. 设∠CMB=α,点C和点D的纵坐标分别为yC,yD,则由例1的解答知 经过思考,可以得到例3的两个变式如下: 仿照例2,得到如下两个问题: 问题2 在问题1中,体积V取到最大值是AB⊥CD的充要条件吗? 对于问题1和问题2,笔者作了探究,并得到如下结论: 证明 设∠CMB=α,椭圆的焦距为2c,点C和点D的纵坐标分别为yC,yD,则直线CD的方程为x=my+r.由例2的解答知 将x=my+r代入椭圆方程,得 (b2m2+a2)y2+2b2mry+b2r2-b2a2=0, 即 1)若q≥0,即r2≤c2,则f′(x)≤0,从而 此时 即AB与CD不垂直. 2003年的全国数学高考试题堪称“史上最难”,时至今日,笔者记忆犹新.理科第18题是一个立体几何试题,是解答题的第2题,当年这道题做出来的考生凤毛麟角.现在回过头来看看,不觉得难,但是为什么当时会难,笔者认为原因很简单,就是因为命题者将平面几何和立体几何结合在了一起.在计算过程中,必须要用到直角三角形中的射影定理,才能看到胜利的曙光,而很多考生都倒在了平面几何上.其实单从结论来说,考生也许都知道,但是能想到两者结合的,可能就不多了. 2015年的浙江省数学高考理科试题第18题是函数试题,是解答题第3题,当年的考生也反映不简单.但是对于一些老教师来说,可能也不觉得新鲜,反而似曾相识,根据老教师反映,类似的试题已经好多年没有出现.而2015年重出江湖的时候,却考倒了一批考生. 由此,当笔者看到例1时,产生了一个疑问:若干年后,二、三个几何知识点的结合体是否会再一次出现在高考卷中呢?就像学考试题那样,用到的平面几何知识并不难.对于圆来说,要联想到平面几何比较自然,那么在解析几何当中,还会自然吗?在解析几何中,如果要利用立体几何的结论,学生还会做吗?如果是3个几何知识点结合起来,考生还依然会处理吗? 笔者认为例1是多个几何知识点的结合,教师要静下心来好好考虑一下:在教学过程中,如何让学生能想到或想到得更加自然.两个几何知识点的结合非常考验学生的能力,要求学生对相关知识非常熟悉,同时也强化了立体几何的传统证明.因此,在今后的教学中,教师可以考虑几个几何知识点结合的综合试题,并原创出更多的好题.在类似的题目出现在高考卷上之前,做到有备无患.

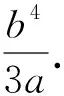

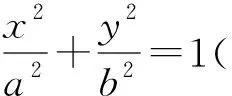



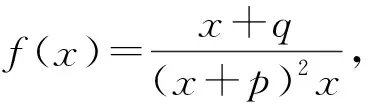

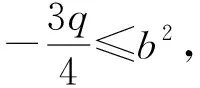
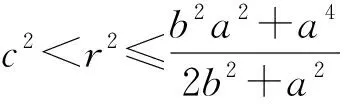
3 一点思考

