一道不被教材淘汰的立体几何题*
●何伟军
(渭源县第一中学,甘肃 渭源 748200)
教材变化已经有几次了,但每次变化都保留了一些经典例题,这些例题体现了基础性、典型性和可接受性,充分利用这些例题及一系列变式,不仅能帮助学生巩固知识、激发学习兴趣、提高分析问题和解决问题的能力,而且还能培育科学精神和创新意识,助推了数学核心素养的培养.
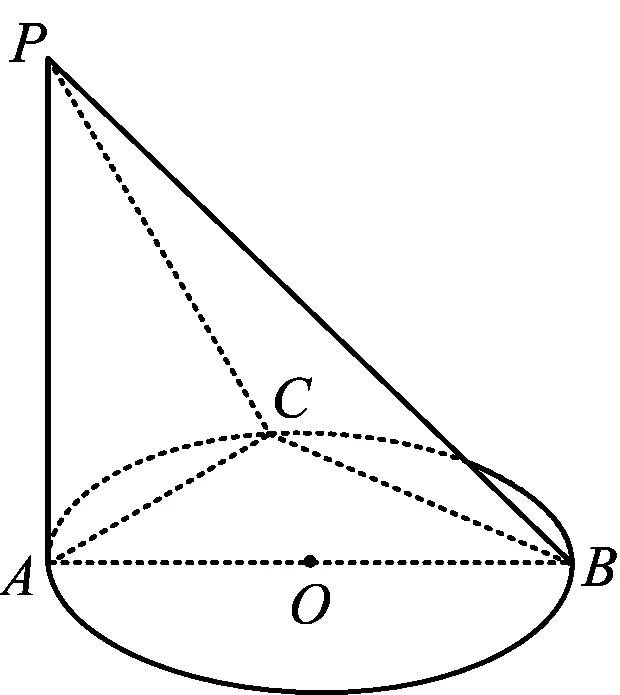
图1
例1 如图1,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆上任意一点,求证:△PAC所确定的平面垂直于△PBC所在的平面.
(人教A版《数学(必修2)》第69页例3)
证明详见课本解答,此处略.
1 解密线面关系,固本溯源
例1只需证明BC⊥AC和BC⊥PA即可,要求学生掌握圆内接三角形的知识、面面垂直的判定定理以及证明面面垂直只需证明线面垂直的技能.以此为契机,以线线垂直、线面垂直、面面垂直的判定为知识基础,编拟一系列关于线面、面面位置关系的问题,对改变学生的认知方式能起到“一叶知秋”的作用;分析掌握其解法,突出知识主线,凸显线面关系垂直的内在逻辑和思想方法,知一类而达全貌,能起到春分化雨、润物无声的作用.不能简单地认为考查的知识点较为单一,简单“不足以应对高考”.去掉底面圆的几何图形,在《九章算术》中将4个面都为直角三角形的三棱锥称之为鳖臑,可以将鳖臑原封不动嵌套在圆柱、圆台、球和其他多面体中.教材基础题是学科核心素养的载体,对发展学生推理论证和空间想象能力、对学生的学习和终生发展有着重要的作用.
2 编制选择题,用好教材
教材是知识的载体,是施教者和受教育者共同的资源,也是命题者寻找“创新题”的引子.回归教材,回归课堂,用好教材,引导学生正确地分析出图形中的基本元素及其相互关系,是培养空间想象能力的重要举措,也真正发挥了教材的示范引领作用与育人功能.
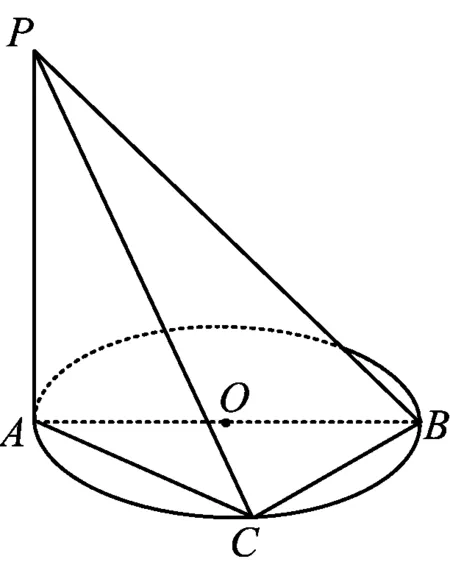
图2
例2 如图2,已知直线PA垂直于以AB为直径的圆(即⊙O)所在的平面,C为⊙O上异于点A,B的任一点,则下列关系中不正确的是
( )
A.PA⊥BCB.BC⊥平面PAC
C.AC⊥PBD.PC⊥BC
分析 选C,过程略.
评注 不难看出,此题是教材变式题,证明BC垂直平面PAC内两条相交直线是关键.
3 编制填空题,做好“试验田”

图3
数学填空题是一种只要求写出结果、不要求写出解答过程的客观性试题,是数学高考中3种常考题型之一,一般可分为:完形填空、多选填空、条件与结论开放的填空题.
例3 如图3,PA垂直于⊙O所在平面,AB是⊙O的直径,C是⊙O上一点,AE⊥PC,AF⊥PB,给出下列结论:①AE⊥BC;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC,其中真命题的顺序号是______.
分析 因为AE⊂平面PAC,BC⊥AC,BC⊥PA,所以BC⊥平面PAC,从而AE⊥BC,故①正确.
因为AE⊥PC,AE⊥BC,PB⊂平面PBC,所以AE⊥平面PBC,从而AE⊥PB.因为AF⊥PB,AE∩AF=A,所以PB⊥平面AEF,又EF⊂平面AEF,于是EF⊥PB,故②正确.
因为AF⊥PB,若AF⊥BC,则AF⊥平面PBC,所以AF∥AE,与已知矛盾,故③错误.
由①正确可知④正确.
综上可知,真命题的顺序号是①②④.
评注 本题源于教材,高于教材.反复在线线、线面垂直的概念、判定和性质定理中来回穿梭、转化,以期实现思辨甄别和推理论证.
填空题是数学高考命题改革的试验田,此类题能较为全面地考查学生的空间想象能力和对立体几何知识掌握的程度,创新型的填空题将会源源不断涌现.求解填空题的基本策略是要在“准”“巧”“快”上下功夫.在备考时,我们既要回归教材,变通教材,又要通过问题的设置,展现思维探究的过程,“多一点想的,少一点算的”,体现新课程研究型学习的理念.
4 扩展成综合题,历练思维品质
例4 如图4,PA⊥平面ABC,点C在以AB为直径⊙O的上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,且OM∥AC.
1)求证:平面MOE∥平面PAC;
2)求证:平面PAC⊥平面PCB;
3)设二面角M-BP-C的大小为θ,求cosθ的值.
(2013年辽宁省数学高考试题第18题改编)
分析 1)已知OM∥AC,关键是证明OE∥PA.
2)关键是证明BC⊥AC,PA⊥BC.

图4 图5
3)如图5,以C为原点、CA所在直线为x轴、CB所在的直线为y轴建立空间直角坐标系C-xyz.因为∠CBA=30°,PA=AB=2,所以
延长MO交CB于点D,因为OM∥AC,所以

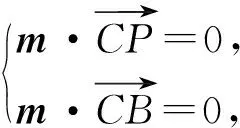
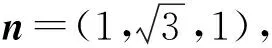

评注 第1)小题考查了面面平行的性质;第2)小题基于例1~例3积累的“数学基本经验”可容易解决;第3)小题求二面角的余弦值,可用向量法获解.证明突出几何法的逻辑推理论证以及空间几何量的计算,强调向量法的运用.
解决这类问题的核心是掌握平行与垂直的判定定理与性质定理,以几何直观图为载体,融入线面关系,不断利用这些定理进行转化,最终证得问题.几何法重在推理论证,向量法侧重“以算代证”,求证的过程中要“四能一会”,即能根据条件作出正确的图形,能根据图形想象出直观形象,能正确地分析出图形中的基本元素及其相互关系,能对图形进行分解、组合,会运用图形与图表等手段形象地揭示问题的本质[1].
《普通高等学校招生全国统一考试大纲的说明》提出:要突出试题的能力立意,坚持素质教育导向.其中,逻辑推理是得到结论、构建数学体系的重要方式,而空间想象能力和图形的转化能力是逻辑推理的必然产物.通过论证、计算,培养学生的探索精神,通过挖掘教材题源功能,还可追问“4)求三棱锥B-PBC的体积;5)求二面角A-BC-P的大小”等,一题多问,一边学一边问,培养学生孜孜不倦的学习品质.
5 编制交汇题,提升空间想象能力
5.1 与圆的交汇

图6
例5 如图6,AB是⊙O的直径,点C是⊙O上异于A,B的点,PO垂直于⊙O所在的平面,且PO=OB=1.
1)若D为线段AC的中点,求证:AC⊥平面PDO;
2)求三棱锥P-ABC体积的最大值;

分析 1)关键是证明AC⊥DO,PO⊥AC.

3)在△POB中,PO=OB=1,∠POB=90°,从而
同理可得
于是
PB=PC=BC.

图7
在三棱锥P-ABC中,将侧面BCP绕PB旋转至平面BC′P,使之与平面ABP共面,如图7所示.当点O,E,C′共线时,CE+OE取得最小值.又因为OP=OB,C′P=C′B,所以OC′垂直平分PB,即E是PB的中点,从而

评注 本题层层设计问题情境,既有“位置关系”的探究,又有“度”的考量.第1)小题根据例1的几何模型知AC⊥BC,只需证明OD∥BC即可;第2)小题求VP-ABC的最大值,只需S△ABC最大,即点C到AB的距离最大;第3)小题在求CE+OE的最小值时,利用“化折为直”的方法解决.如丝如扣、步步为营的分析成为培养“逻辑推理”的绝佳素材.
立体几何与圆的交汇问题,经常利用“圆的直径所对的圆周角为直角”这一性质,在解题中充分体现了“直观感知、操作确认、思辨论证、度量计算”基本方法的考查,如折叠问题展现了立体几何中平展与翻折的方法,实现了空间问题平面化.
5.2 三视图的交汇
例6 一个几何体的三视图如图8所示,则该几何体的外接球的表面积为
( )
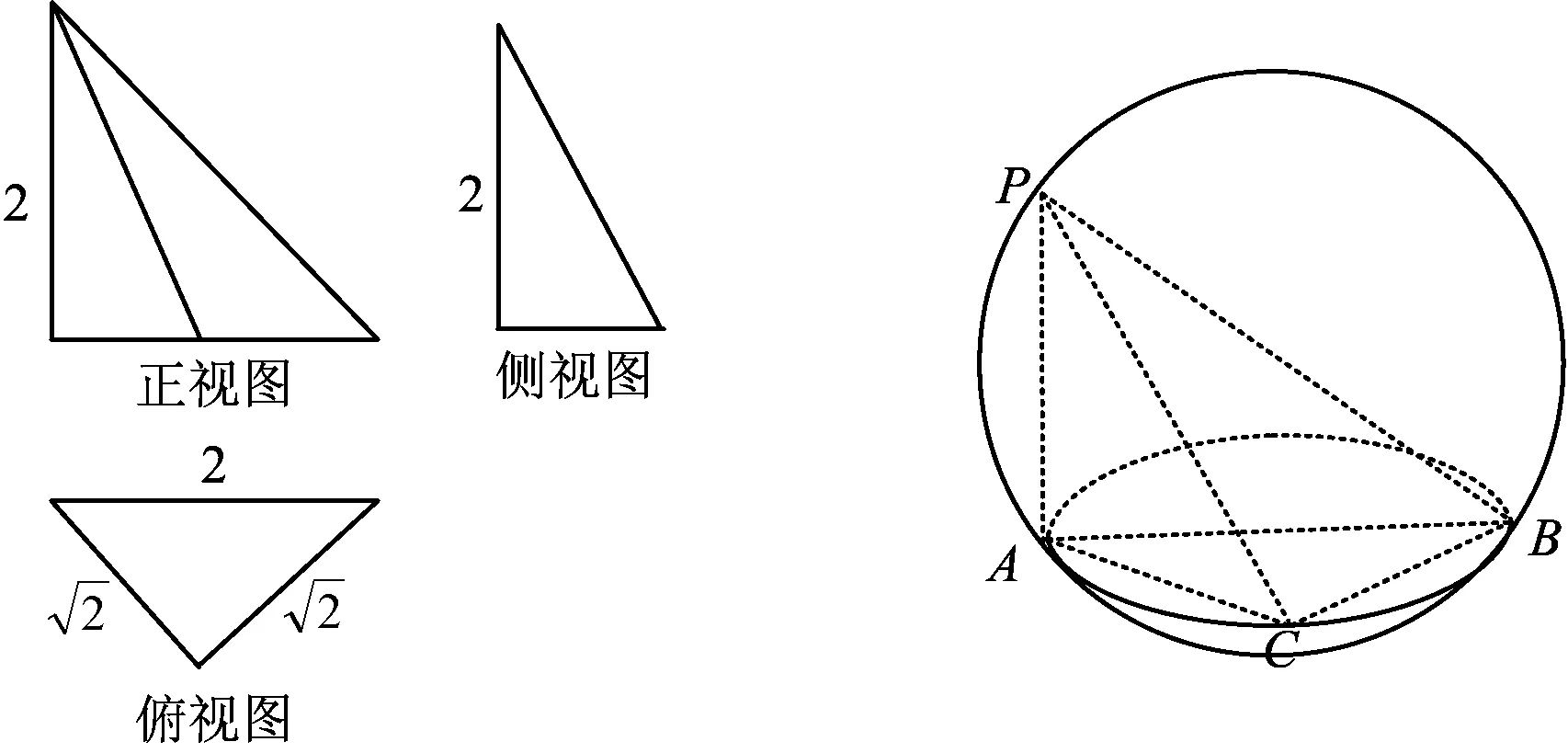
图8 图9
分析 根据几何体的三视图,得该几何体是底面为等腰直角三角形、高为2的三棱锥,如图9所示,该三棱锥的外接球是对应直三棱柱的外接球.
设外接球的半径为R,因为底面是等腰直角三角形,所以外接圆的半径为1,从而R2=1+1=2,于是外接球的表面积是4πR2=8π,故选B.
评注 柱体的外接球问题,其解题关键是能根据题意画出直观图,并能在图形中找到球心在多面体中的位置,找到球半径或直径与多面体相关元素之间的关系,结合原有多面体的特性求出球的半径,然后再利用球的表面积和体积公式进行正确计算.
以三视图为教学情境,启发学生根据条件对图形进行还原,想象出直观图形,这样的空间想象能力的培养不可忽视,而且是要长期坚持的,如此才能促进学生实践能力和创新意识的发展.
5.3 与三角函数的交汇

图10
例7 如图10,AB是⊙O的直径,点C是⊙O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.
(2013年湖北省数学高考理科试题第19题)
分析 1)直线l∥平面PAC,过程略.

图11
2)方法1 (综合法)如图11,联结BD,由第1)小题可知交线l即为直线BD,且l∥AC.因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l⊂平面ABC,于是PC⊥l.而PC∩BC=C,故l⊥平面PBC.
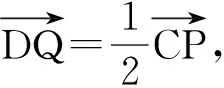
联结PQ,DF,因为F是CP的中点,CP=2PF,所以DQ=PF,从而四边形DQPF是平行四边形,PQ∥FD.
联结CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,故∠CDF=θ就是直线PQ与平面ABC所成的角.
又BD⊥平面PBC,即BD⊥BF,知∠BDF为锐角,故∠BDF为异面直线PQ与EF所成的角,即∠BDF=α,于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得
从而
即
sinθ=sinαsinβ.

图12

于是
取平面ABC的一个法向量为m=(0,0,1),得

取n=(0,c,b),则
从而

即
sinθ=sinαsinβ.
评注 第2)小题用几何方法,联结DF,很快就可以求证.用空间向量法求异面直线所成角、线面角、二面角的平面角,通过数学抽象成向量(法向量)的夹角,进而求解.
以教材的例题为引子,设计线面关系的判定题并加以证明,体现了知识的交汇性,又将空间角融合在同一道题目之中,扩容了知识点,突出了高考命题的重点.
6 教学反思
6.1 回归教材,夯实基础,充分依托和挖掘教材内容
回归教材,寻找高考“母题”,以“母题”为载体知识、方法基础并不过时.从浅层次去挖掘,学会有效观察、感觉、联想、对接、迁移和转化,学会细研基础题,获得基础知识、基本方法、基本技能和基本经验,这样的教学形成的解题通法并不过时,况且接近教材、符合学情的教学是深得民心的,尤其是对于文科考生.
6.2 基于教材的改造、改编的考题凸显能力的高低
基于教材的变式题,以至于高考真题,都是教材演绎的新问题.通过探究高考题目的生长点可以发现,载体有时发生变化,但最基本、最简单的空间图形没有变,如题源三棱锥是一个极其重要的立体几何模型,模型中位置关系、度量关系没变,可以嵌套于球体中,也可以嵌套于柱体中,而且解决问题的思想方法没有变,直击数学运算、直观想象和逻辑推理的核心素养培养.千变万变,不离其宗.
6.3 培养学生的创新能力,提升学生的数学素质
通过对题源嵌套、迁移、组合、扩展等方法,培养学生知识迁移能力和创新意识,通过对问题探究的解答,培养学生创新能力和科学探索的精神.立体几何的解答题常常采用“先证后建系”的方式构建试题,它在发展几何直观能力和考查空间想象能力上是其他内容不可替代的,逻辑推理能力考查必然是空间线面位置关系的证明和空间角的计算(文科多为几何体的体积),积累思维和实践的经验,为有效解题提供保障.在这个教学过程中,学会用数学眼光观察几何体,提倡独立思考,探索交流,提供方法,感悟知识本质,达成共识,找规律,促转化,落实立德树人的根本任务.

