基于支持向量回归的金属谐振陀螺多元温度补偿方法

韦俊新，王泽涛，丛 正，魏艳勇，齐国华

（天津航海仪器研究所，天津 300131）

金属谐振陀螺是一种基于哥式效应的固体波动陀螺，具有寿命长、精度体积比较高、可靠性高、成本低等特点，在各个领域具有广阔的应用前景。

全温特性不理想是制约金属谐振陀螺工程化的一个重要因素。温度变化严重影响了陀螺的零偏稳定性等性能。改善陀螺温度特性包括硬件补偿和软件补偿，硬件补偿不仅增加系统体积和成本，而且实现难度较大，软件补偿具有方便易实现等优点，故实际应用通常采取软件补偿方式。

陀螺温度特性一般受多种因素影响，文献[1]针对激光陀螺建立了基于温度-温变速率-温度梯度的多元温补模型，补偿后的陀螺精度提升数倍。

随着智能算法的逐步兴起，用来模拟和补偿陀螺漂移的方法越来越丰富。神经网络是常用的智能算法，在随机漂移建模中取得了良好的效果[2-3]。但在训练过程中可能存在过度拟合问题，隐藏层中的节点数量取决于经验而缺乏理论指导[4]。相比神经网络，支持向量机（SVM）具有更好的抗过拟合能力和回归能力。文献[5]采用最小二乘支持向量机建立模型，补偿后陀螺精度提升约一个数量级；文献[6]采用一种基于改进支持向量机的多尺度建模和回归方法，回归精度提升了两个量级。

本文基于金属谐振陀螺工作原理，对其温度特性进行机理分析和仿真研究，综合考虑各种建模方法与补偿模型，提出一种基于支持向量回归的多元温度补偿方法，建立温度-温度变化率-温度梯度补偿模型，最后进行实验验证，并对比该方法的补偿效果。

1 工作原理及温度特性分析

金属谐振陀螺的结构如图1(a)所示，它包括基座、谐振子、压电陶瓷及外壳。谐振子包括谐振环及导振结构，分别用于产生陀螺效应和振动传递；底部均匀分布八个圆孔，具有抑制各阶模态耦合的作用；底面粘有四对压电电极，分别用于激励和检测。

图1 金属谐振陀螺结构与工作原理Fig.1 Metal resonant gyro structure and working principle

金属谐振陀螺的工作原理如图1(b)所示。给相对的两个压电电极施加与谐振子固有频率相同频率的交变电压，激励出谐振子的驱动模态，此时波节点处压电输出为零。当陀螺敏感轴方向有角速度输入时，在科氏力的作用下激励出陀螺的敏感模态，此时波节点处压电产生输出信号，检测该信号即可得到外界输入角速度大小。

可见，金属谐振陀螺是一种基于科氏效应的固体波动陀螺。当温度变化时，谐振子材料的非理想因素会引起与温度相关的额外误差项，导致陀螺输出发生漂移[7]。

当谐振子处于谐振状态时，谐振子振动生热，假设外界环境温度为T2，谐振子温度为T1，稳态时有T1＞T2，热传导过程如图2所示。热量将从陀螺内部传导至外界进而达到动态平衡，有热传导公式：

图2 热传导过程示意图Fig.2 Schematic of heat conduction process

式中，Φ为热流量，K为当量导热系数，A为传热面积，ΔT=T2-T1，L为导热距离。图3(a)为谐振状态时，谐振子的温度分布状态仿真图。显然，谐振环与谐振子底部存在温度梯度，因温度传感器的布置不能影响核心敏感元件谐振子的振动状态，所以温度传感器与谐振子必然存在温度梯度。

当外界环境温度由T2升至T2′稳定后，假设T2′ ＞T1，热量将从外界传至谐振子，谐振子温度t时间后稳定至T1′。图3(b)为谐振子在不同时刻的温度分布图，在传热过程中，谐振子总热能可表示为：

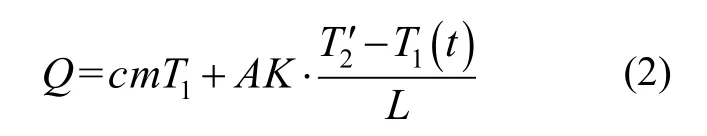
式中，c为谐振子比热容，m为质量，T1（t）为传热过程中谐振子温度随时间的变化，稳定后为T1′。当外界环境温度变化率不同时，相同时间内T1（t）不同，即谐振子温度不同，进而影响陀螺输出。

综上，当温度、温度变化率及温度梯度变化时，都会在一定程度上引起陀螺输出的改变，并且这些指标都具有一定随机性，因此有必要采用措施综合考虑这些指标，并建立多元补偿模型进行补偿，并且支持向量机具有抑制数据随机性的特点。多元补偿模型可表示为：

其中，Y为陀螺输出，T为温度，dTdt为温度变化率，ΔT为温度梯度。

2 模型建立

2.1 实验及测试系统

为获取陀螺输出随温度变化的原始数据，搭建了全温区实验平台，如图4所示，包括温箱EG-02KAS、数字万用表34401A、温度传感器Pt1000、计算机及测试软件。

温度循环示意图如图5(a)所示，升降温阶段变化率都为1℃/min，保温时间为1 h。

图4 测试系统实物图Fig.4 Physical map of the test system

图5 温度循环曲线及陀螺输出Fig.5 Temperature cycle curve and gyro output

实验数据如图5(b)所示，结果表明：陀螺输出与温度呈规律变化，全温区范围内共变化约398.3 (°)/h，难以满足工程应用的需求。图中输出与温度存在明显的对应关系，可通过建立适当的数学模型对陀螺进行温度补偿。

2.2 小波去噪

由于陀螺输出原始数据噪声较大，对模型拟合精度影响较大，因此在建模前先对实验数据进行预处理。

小波变换具有低熵性、多分辨率、去相关性、选基灵活性等特点，在去噪算法中被广泛应用。本文采用小波域阈值法[8-9]，其具有实现简单、计算量小等优点，不但能较好地抑制噪声，还能保留原始信号的突变点，达到出色的去噪效果。去噪步骤包括噪声信号分解、小波系数估计和有效信号重构。

本文采用 sym5小波基对信号进行噪声分解，以减少小波对信号进行分析和重构时的相位失真。消噪后的数据如图6所示，可以看出既保留了原始数据的趋势，又具有较好的去噪效果。

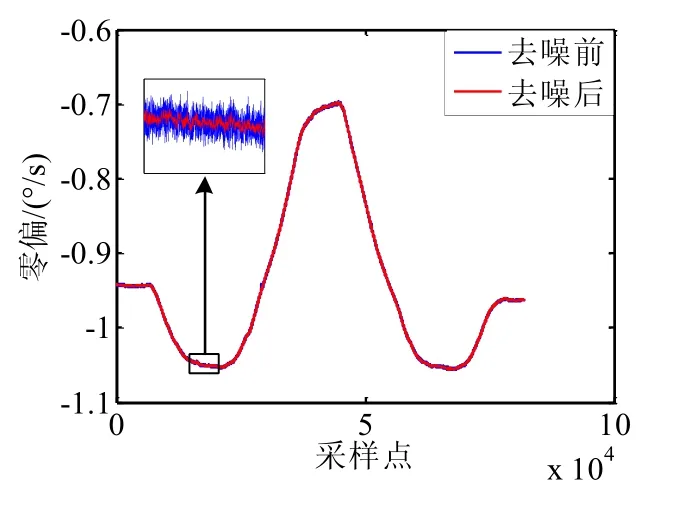
图6 小波去噪前后对比Fig.6 Comparison before and after wavelet denoising

2.3 模型建立及优化

考虑到温度、温度变化率及温度梯度交叉项因素，采用多项式模型，阶数取3。模型(3)可展开为：

本文采用最小二乘法求解模型各阶拟合系数，具体过程不再赘述。最小二乘估计的一般形式为：

其中，β是模型各项系数组成的列向量，是其最小二乘估计，X为式(4)中由各变量组成的行向量。

获得各项系数后，多元补偿模型已基本确定。除常数项外，该模型共包含17个变量，计算量较大，因而通过多元线性逐步回归法分析模型各变量与陀螺漂移间的显著程度，进行模型优化。若变量与输出无相关性，则剔除该变量。故优化后的模型可表示为：

3 基于支持向量回归的多元补偿模型

支持向量机在解决小样本、非线性和高维模式识别问题中有许多优势，在特征提取、分类识别、回归计算等领域都得到了广泛应用[10]。如前所述，陀螺在实际应用中，环境变化具有随机性，本文采用支持向量机对陀螺输出进行特征提取，降低随机误差。

支持向量机的原理就是在已知的两类线性可分的数据样本中找到一个最优分类面，两类数据样本可通过该面得到最大化分割。如图7所示，假设图中的圆和正方形分别为两种数据样本，H为分类线，将H平行移动从而得到边界位置H1及H2，最优分类面不仅可以将两类数据样本正确分隔开，使训练错误率为零，而且还应确保两类数据样本间的分类间隔达到最大。

图7 最优分类面示意图Fig.7 Optimal classification surface diagram

设 { (xi,yi) ,i= 1,,n} ,xi∈R,yi∈{1,-1}为 两 类线性可分的数据样本，其中，xi为输入特征向量，yi为输入特征向量的类别标记。f（x）=ω·x+b为线性判别函数的一般形式，因此可得到对应的分类面的表达式：

通过直接计算能够得知，此时H1与H2之间的距离为即此刻分类间隔为若使间隔最大，即为使最小。故可将求解两类数据样本的最优分类面问题转化为如式(8)所示的求解变量ω与b的最优化问题：

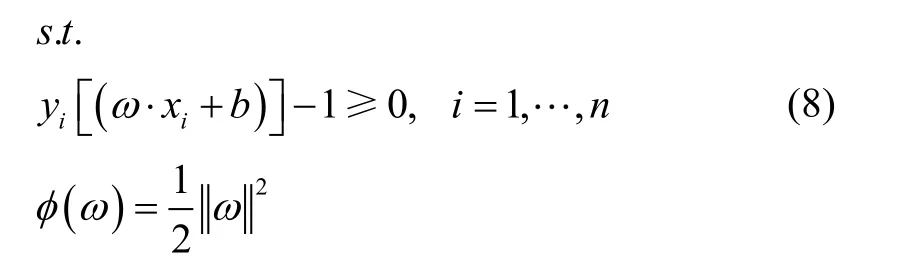
根据金属谐振陀螺的输出曲线，提取陀螺输出趋势项，显然属于求解非线性数据最优化的问题。对于线性不可分的数据样本，需要通过核函数将数据映射到高维特征空间，将复杂的非线性问题转换为简单的线性问题，然后通过求解线性问题得到原问题的解，核函数作为映射函数在转化过程中起到至关重要的作用。上述最优化问题变为：

其中，C称为惩罚因子，ξi称为松弛因子。C的值越大，表明回归效果越好。

随着SVM的不断进步，核函数对数据特征提取的影响越来越大，因此在对陀螺输出进行特征提取时，核函数的选取十分关键。为得到陀螺输出曲线微小变化的特征，本文采用具有较强的局部描述能力的径向基核函数对实验获取的数据进行特征提取，径向基核函数表达式为：

式中，σ为核函数宽度，其值越小就具有越强的局部描述能力。结果如图8所示。

实验数据经特征提取后，最终得到一组综合各组数据微小差异的陀螺输出。表1列举出了支持向量机特征提取后的陀螺输出与各组实验数据间的方差。

图8 支持向量回归Fig.8 Support vector regression

表1 SVM后输出与各组实验数据之间的方差Tab.1 Variance of the SVM output and the experimental data of each group

基于特征提取后的数据与式(6)，再解算出各项系数，便可得到基于支持向量回归的多元补偿模型。

4 补偿结果对比及分析

为验证所建立两模型补偿效果，建立了传统温度-输出模型，并对比了基于温度模型补偿、优化后多元模型补偿与基于支持向量回归的多元模型补偿的补偿效果。

4.1 补偿结果

4.1.1 基于温度模型补偿

基于温度的多项式补偿模型可表示为：

其中，C0为温度非相关项，阶数取n=3。

补偿结果如图9(a)所示。经温度模型补偿后，陀螺全温区性能得到改善。补偿前后，陀螺的最大零偏漂移由 0.36 (°)/s 减小到 0.105(°)/s，零偏稳定性由398.3 (°)/h 提高到 90.7 (°)/h。

图9 a 基于温度补偿模型的补偿效果Fig.9 a Compensation effect based on temperature compensation model

4.1.2 优化后的多元模型补偿

由于谐振子与外界发生热交换需要一定时间，导致谐振子温度与外界温度存在温度梯度，使得陀螺出现迟滞效应。外界温度变化越剧烈，迟滞效应越严重，影响陀螺输出。采用多元补偿模型可减小迟滞效应的影响。

补偿结果如图9(b)所示。陀螺的最大零偏漂移由0.36 (°)/s 减小到 0.0317 (°)/s，零偏稳定性由 398.3 (°)/h提高到 22.6 (°)/h。

图9 (b) 多元补偿模型补偿效果Fig.9 (b) Multi-compensation model compensation effect

4.1.3 基于支持向量回归的多元模型补偿

基于支持向量回归的多元模型补偿结果如图9(c)所示。陀螺的最大零偏漂移由0.36 (°)/s 减小到0.022 (°)/s，零偏稳定性由398.3 (°)/h提高到17.7 (°)/h。

图9 (c) 基于支持向量回归的多元补偿模型补偿效果Fig.9 (c) Compensation effect of multivariate compensation model based on support vector regression

4.2 验证及结果分析

为验证本文提出的基于支持向量回归的多元补偿模型补偿效果，再次用三种模型对另一组实验数据进行补偿，效果对比如图10所示。陀螺零偏稳定性由补偿前的 420.2 (°)/h 分别提高到 84.4 (°)/h、27.2 (°)/h及 23.7 (°)/h。

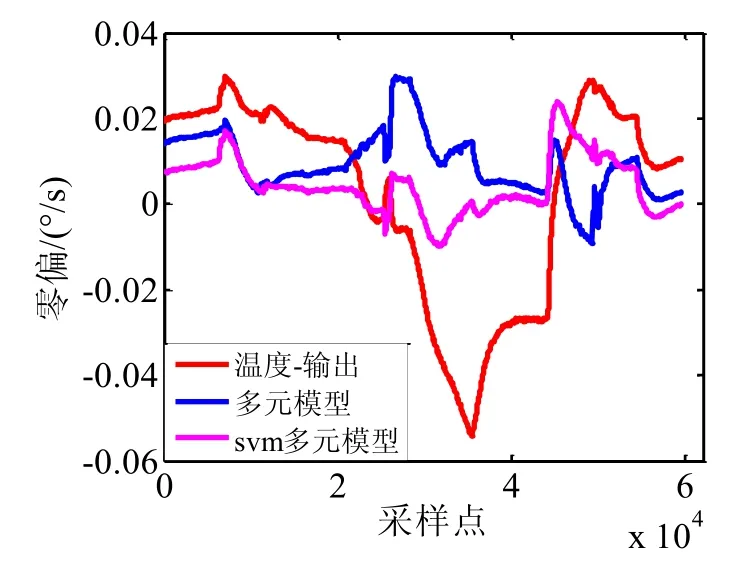
图10 补偿结果对比Fig.10 Comparison on compensation results

验证结果表明：基于支持向量回归的多元补偿模型补偿效果最佳。基于温度的补偿模型只能补偿陀螺随温度缓慢变化的主体趋势，在温度转折点处补偿效果较差；引入温度梯度与温度变化率作为模型变量后，较好地补偿了温度改变时的输出，并补偿了大部分的滞后效应。通过支持向量回归对实验数据进行特征提取，并基于此建立多元补偿模型，使补偿后的精度得到进一步提升。

5 结 论

对于陀螺仪而言，全温精度是衡量其性能的重要指标。本文基于实际实验数据，采用多项式模型，建立了一种基于支持向量回归的多元补偿模型。通过实验对比了模型补偿效果，结果表明，该模型补偿效果明显优于常规模型，较大程度上改善了陀螺性能，与补偿前相比，零偏稳定性提高一个数量级以上。