七沟道球笼式等速万向节等速性分析
谢鲲,闫公哲
(1.上海应用技术大学 轨道交通学院,上海 201418;2.华东理工大学 机械与动力学院,上海 200237)
球笼式等速万向节是轿车关键零部件之一,其直接关系汽车转向驱动性能。创新设计的七沟道球笼式等速万向节由于耗材低,又能满足节能、轻量、环保、可靠性高等要求,成为等速万向节及传动轴总成优化设计的最佳选择[1-4],关于七沟道球笼式等速万向节的研究并未涉及运动学方面的内容。鉴于此,通过建立七沟道球笼式等速万向节的运动学模型,证明了球笼式等速万向节的等速性,并分别计算了钢球在沟道内的瞬时角速度随输入轴转角及输入轴与输出轴夹角的变化规律。
1 球笼式等速万向节运动学模型的建立
七沟道球笼式等速万向节结构如图1所示,星形套外球面与相应的球笼式保持架内球面配合,钟形壳内球面与相应的球笼式保持架外球面配合,4个内、外球面组成了 2 组绕同一球面中心转动的球面副,该球面中心与输入轴( 星形套) 和输出轴( 钟形壳) 两轴的交点重合[5]。为分析球笼式等速万向节的运动规律,同时实现模型可计算性,做如下假设:1)球笼式等速万向节为理想结构,不考虑星形套内沟道、钟形壳外沟道形状及加工误差;2)球笼式等速万向节为完全刚体,钢球与星形套内沟道接触,钢球与钟形壳外沟道接触,钢球与保持架窗口上下面接触均可用质点来代替;3)不考虑钢球、星形套内沟道、钟形壳外沟道在运动过程中受力产生的变形。

图1 七沟道球笼式等速万向节结构

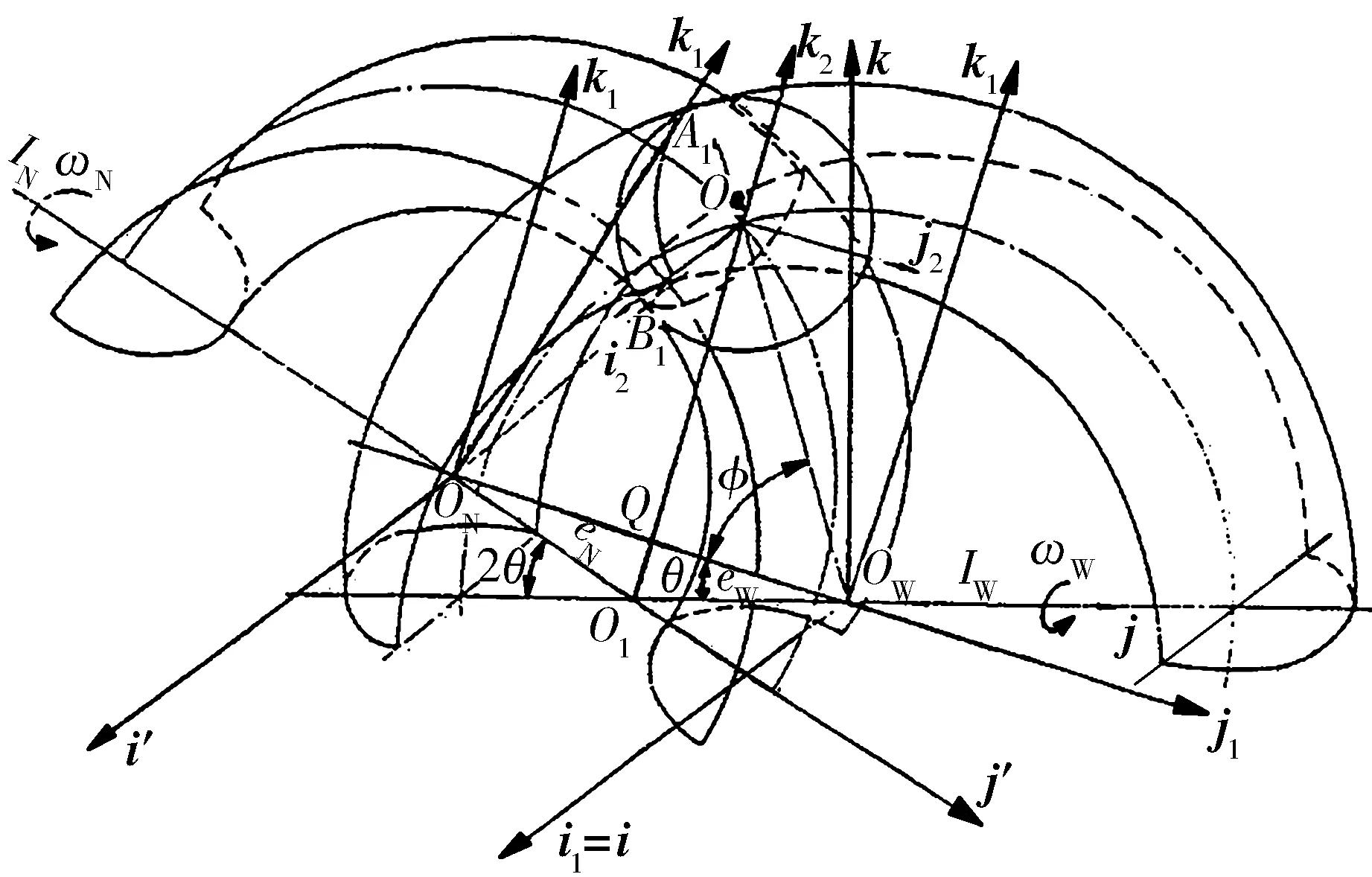
图2 一组钢球和沟道的接触模型
在△OJONOQ(或△OJOWOQ)中,由余弦定理可得
(1)
2 七沟道球笼式等速万向节等速性理论分析
2.1 星形套与钢球的运动关系
钢球与星形套的接触示意图如图3所示,星形套与钢球的接触点为N,在接触点星形套椭圆曲面切面与钢球球面切面的夹角为α,在钢球坐标系ρN中接触点N可表示为
rN=i′(RQcosαcosδ-RQsinαsinφsinδ+RQsinφsinδ)+j′(-RQsinαcosφcosθ+Rg·
cosφcosθ+RQcosαsinθsinδ+RQsinαsinφ·
cosδ-Rgsinφsinθcosδ)+k′(-RQsinαcosφ·
cosθ+Rgcosφcosθ+RQcosαsinθsinδ-RQsinα·
sinφcosθcosδ+Rgsinφcosθcosδ),
(2)
式中:RQ为钢球半径;δ为输入轴绕j1轴的旋转角度。
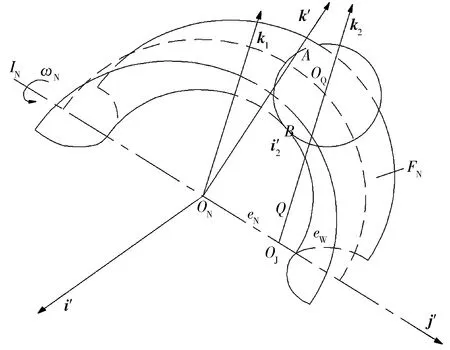
图3 钢球与星形套接触示意图
在钢球坐标系ρQ中过接触点N的法向量可表示为
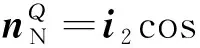
(3)
将其转化到坐标系ρN中为
nN=i′cosαcosδ-sinαsinφsinδ+j′·
(-sinαcosφcosθ+cosαsinθsinδ+sinαsinφ·
sinθcosδ)+k′(-sinαcosφsinθ-cosαcosθ·
sinδ-sinαsinφcosθcosδ)。
(4)
星形套椭圆曲面在接触点N的角速度为ωN,则线速度为
VN=ωN·rN,
(5)

VN在nN方向的分量为
VN·nN=ωN(Rgcosαcosφsinθcosδ+Rg·
cosαsinφcosθ)。
(6)
在ρN1坐标系下钢球角速度为
ωQ=j1ωQ,
(7)
式中:ωQ为钢球角速度。
在ρN1坐标系下钢球线速度为
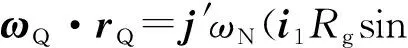
(8)

sinφcosδ,
转换到ρN坐标系下为
sinδsinθ)+k(-RgωQsinφcosθsinδ),
(9)
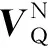
(10)
星形套内沟道与钢球在接触点处2个共轭曲面在法向方向的线速度相等,由(6),(10)式可得
ωQ=ωN(cotφsinθcosδ+cosθ)。
(11)
2.2 钟形壳与钢球的运动关系
钢球与钟形壳的接触示意图如图4所示,钟形壳与钢球的接触点为W,在接触点钟形壳椭圆曲面切面与钢球球面切面的夹角为α,在坐标系ρW中接触点W可表示为
rW=i(-RQcosαcosδ+RQsinαsinφsinδ+Rgsinφsinδ)+j(-RQsinαcosφcosθ-Rgcosφ·
cosθ+RQcosαsinθsinδ+RQsinαsinφsinθcosδ+Rgsinφsinθcosδ)+k(RQsinαcosφsinθ+Rg·
cosφsinθ+RQcosαcosθsinδ+RQsinαsinφ·
cosθcosδ+Rgsinφcosθcosδ)。
(12)
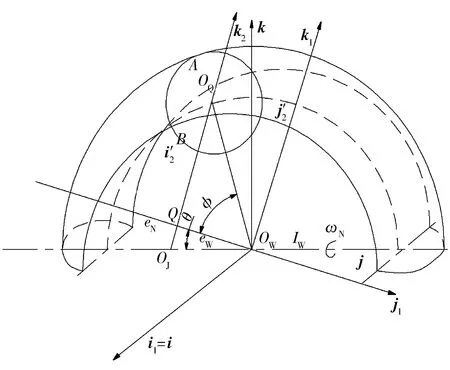
图4 钢球与钟形壳接触示意图
在钢球坐标系ρQ中过接触点W的法向量为

(13)
该矢量在ρW坐标系可表示为
nW=i(-cosαcosδ+sinαsinφsinδ)+j·
(-sinαcosφcosθ+cosαsinθsinδ+sinαsinφ·
sinθcosδ)+k(sinαcosφsinθ+cosαcosθsinδ+sinαsinφcosθcosδ)。
(14)
钟形壳在接触点W的角速度为ωW,线速度为
VW=ωW·rW,
(15)
ωW=jωW,
VW在nW方向上的分量为
VW·nW=-ωW[Rgcosαsinφcosθ+Rg·
cosαcosφsinθcosδ]。
(16)
在ρW1坐标系下钢球角速度为
ωQ=j1ωQ,
(17)
在ρW1坐标系下钢球线速度为
VQ=ωQ·rQ=i1Rgsinφsinδ-j1Rgcosφ+k1Rgsinφcosδ,
(18)

k1Rgsinφcosδ,
转换到ρW坐标系下为
sinδsinθ)+k(-RgωQsinφcosθsinδ),
(19)
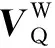
(20)
钟形壳和钢球在接触点处2个共轭曲面在法向方向的线速度相等,由(16),(20)式可得
ωQ=ωW(cotφsinθcosδ+cosθ)。
(21)
由(11),(21)式可得ωN=ωW。输入轴与输出轴角速度始终相等,证明了球笼式等速万向节的等速性。
2.3 钢球角速度
取ωN=314 rad/s,通过MATLAB对上述理论分析进行仿真,钢球角速度ωQ随转角δ、输入轴与输出轴之间的夹角2θ的变化如图5所示,由图可知:钢球角速度ωQ随转角δ呈周期性变化;钢球角速度ωQ随轴间夹角2θ增大而减小,在夹角为0°,35°的2种情况下,角速度ωQ分别取最大值和最小值。
3 仿真分析
以某七沟道球笼式等速万向节为研究对象,其主要结构参数见表1。

图5 钢球角速度ωQ随转角δ和轴间夹角2θ的变化规律
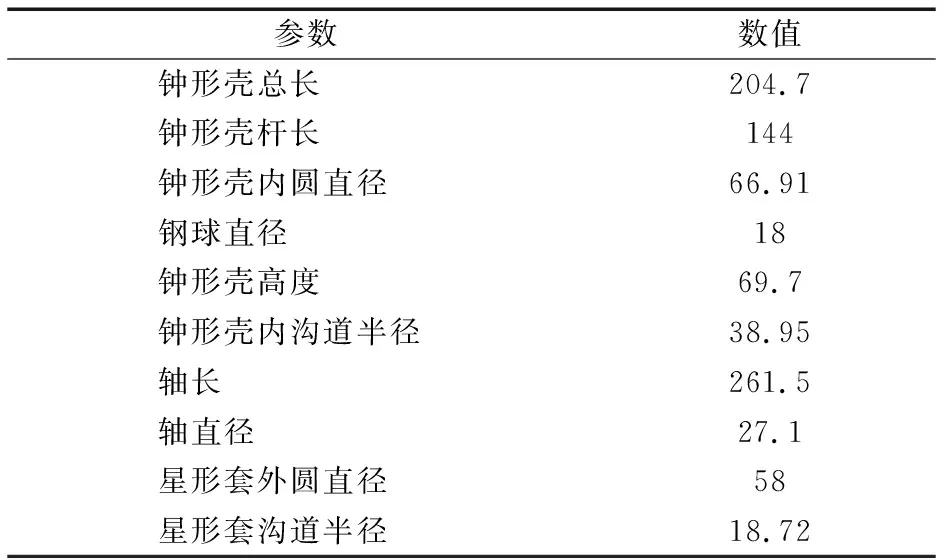
表1 七沟道球笼式等速万向节主要结构参数
基于SOLIDWORKS建立三维模型,将球笼式等速万向节轴间夹角分别设置为0°,35°,得到三维模型如图6所示。基于ADAMS进行多体动力学仿真时做如下假设[8]:1)球笼式等速万向节各零部件均为刚体。2)输入轴与星形套连接。将建立的三维模型导入ADAMS。球笼式等速万向节星形套角速度为6.28 rad/s,为保证受力平衡,在输出轴端与输入端设置等大的反向转矩,输入轴最大输入转矩为125 N·m。设置仿真时间1 s,仿真步长为0.001 s。
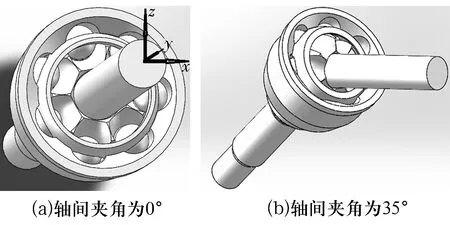
图6 七沟道球笼式等速万向节三维模型
通过仿真分析得到七沟道球笼式等速万向节在轴间夹角为0°,35°时星形套、保持架和钟形壳的角速度变化规律如图7所示,由图可知:在球笼式等速万向节运行过程中,输入轴端星形套、保持架和输出轴端钟形壳角速度近似相等,满足球笼式等速万向节传递角速度不变的运动特征。

图7 星形套、保持架和钟形壳的角速度变化规律
4 结束语
通过理论分析建立了七沟道球笼式等速万向节运动学模型,证明了球笼式等速万向节等速性原理,并通过运动学仿真对理论分析结果进行验证,证明了其理论分析的正确性。分析结果可为七沟道球笼式等速万向节设计和应用提供参考。

