载重子午胎与沥青混凝土桥面全耦合瞬态接触响应的数值模拟

李志栋，黄晓明

（1.中交第一公路勘察设计研究院有限公司，陕西 西安 710075；2.高寒高海拔地区道路工程安全与健康国家重点实验室，陕西 西安 710075；3.东南大学 交通学院，江苏 南京 210096）

0 引 言

桥面沥青铺装系结构设计的目的在于对其长期性能进行验算和控制，但需通过试验、道路长期运行建立病害与临界响应间的关系来控制，耗时太长，不容易实现。因此，人们通过试验实测轮胎和桥面接触响应分布或采用有限元模拟技术实施数值分析，主要包括3类方法。

第一类：完全响应数值模拟。基于层状体系采用有限元软件对胎／面静态、瞬态接触力学响应进行模拟，并进行长期性能预测；其准确性取决于选取结构、材料本构的完善程度，受到计算时机与模型精确性之间矛盾的制约［1－3］。

第二类：瞬态响应实测。如欧盟COST 334计划（2001）及 Al-Qadi等［4－5］在 弗 吉 尼 亚 进 行 的SMART试验路计划（2004）。

第三类：长期性能测量。采用加速加载试验进行长期性能观测（即 ALT 试验）［6－9］。

考虑到第二、三类方法费用太高、耗时太长，而胎／面静态接触响应又不能完全、真实地表征胎／面接触受力状态，所以本文基于ABAQUS软件对传统11R22.5及新型425／65R22.5宽基胎分别与弯坡桥沥青铺装系的全耦合瞬态接触响应进行模拟，从而为混凝土桥面沥青铺装层设计、施工控制起到指导作用。

1 建立载重子午胎与混凝土弯坡桥3D模型

1.1 建立载重子午胎3D有限元模型

根据桥面沥青铺装系实际空间受力情况，基于ABAQUS／CAE直接建立3D轮胎模型，然后与桥面3D模型进行全耦合。

1.1.1 绘制整胎sketch断面图

在ABAQUS／CAE中Model的Schech上绘制Tread、Ply、Belts、Rim 的 2D 断 面，然 后用 Add Sketch在各部件3D建模中重复加载断面图，再根据需要删减各部件多余断面，结果如图1所示。

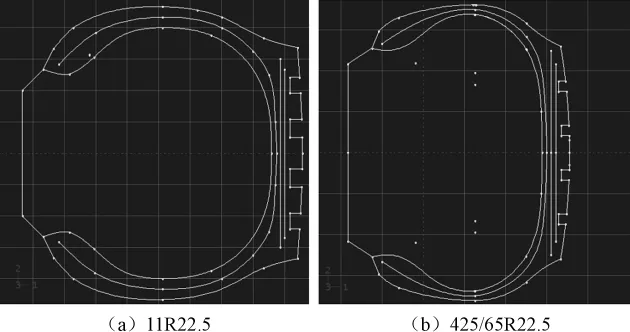
图1 宽基胎有限元断面

建立Part的3D模型：采用Part模块3D（Modeling pace）、Deformable（Type）、Solid（适用 Tread）或 Shell（适用 Belts、Ply）、Revolution步骤进入Sketch界面，依次完成如图2所示Belts（2层为一个Part）、Ply、Rim、Tread部件。

图2 载重子午胎所有部件

1.1.2 定义材料属性

（1）进入 Material Property依照Elasticity-Hyperelastic-Yeoh模型Coefficients定义Tread超弹性模型及Belts、Ply弹性模型，参数见表1。

（2）定义Section属性，壳部件Belt、Ply须定义Shell截面Homogeneous属性，切忌选择Surface或Memberane属性；因Belt与Ply均属橡胶里铺设钢丝和纤维加筋层，定义Shell截面时需在Rebar Layer的constant由Rebar单元描述钢丝和纤维位置、性质、形状等，参数见表2。

表1 轮胎部件材料模型及材料参数

表2 Belts与Ply中rebar单元参数

1.1.3 设置分析步

总分析时间设为1、最小时间步设为0.1，以满足非线性的轮胎预压、充气、加载步。稳态滚动分析时，总分析时间不宜太长，由滚动线速度v确定，如10km·h－1滚动0.1s（约1个轮胎印迹纵向长度），60km·h－1滚动0.02s即可，否则计算成本极高且不能收敛，最小时间步设为0.001～0.002s较合理，也可由最大分析步数来限定滚动距离。在稳态滚动分析时宜分预压、充气、加载、制动、驱动多分析步，机时稍长，但更精确，其边界条件不易过约束，这样更易查找问题。

1.1.4 定义接触与加载

定义接触后，按预压与加载荷载步分别定义加载，并通过桥面板施加预压和加载，也可通过桥面板位移边界条件或微小荷载实现。

1.1.5 网格划分

由于轮胎由多个不同厚度和结构的不规则断面部件组成，网格划分非常之难。网格稍大会导致单元过度扭曲而不收敛，故不同轮胎需通过划分不同网格反复进行尝试，本文将11R22.5胎面网格为0.017m×0.016m，共19 715个单元，27 655个节点；而425／65R22.5胎面网格划分为0.022m×0.018 m，共48 280个单元，222 894个节点。

1.2 建立弯桥3D有限元模型

1.2.1 建立弯桥模型

通过ABAQUS／CAE建立跨长20m、跨中有0.3m宽横隔板、跨间有2m横隔板、底部有直径为1.5m支座、圆曲线半径为200m的3D弯桥模型。

两跨模型由半径均为200m的4个半跨（4×8.85m）、3个2m跨间横隔板及2个跨中横隔板组成，建模过程中注意：与轮胎建模的坐标系不同，桥面坐标系1（x）为横向（垂直行车方向）、2（y）为竖向、3（z）为纵向（行车方向）；采用 Revolution将横断面Sketch沿水平方向分别旋转2.536 6°、0.573 2°、0.086°形成半跨、跨间横隔板、跨中横隔板模型。

图3 两跨连续梁主梁及横隔梁段模型

1.2.2 建立连续两跨模型

为确定最不利荷位，同时对常规直线型与弧型汽车列车荷载进行对比，考虑到轴距、轮距及弯桥内外半幅响应的区别，建立两跨连续梁模型，模型底板支座位置采用Partition划分，并约束两跨端部全部自由度。但由于整梁同时受到弯、扭变形作用，所以箱梁底板不宜全部固支约束，应按照不同支座类型在支座处进行相应自自由度约束，结果见图4。

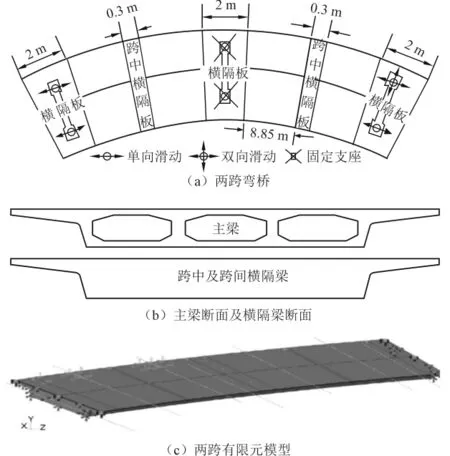
图4 混凝土单箱三室箱梁断面及连续两跨有限元模型

1.3 建立胎／面全耦合模型

本文针对小跨径混凝土连续箱梁桥整体结构刚度大的特点，建立横向半幅宽度7.75m、纵向20m（含1个横隔板、1个跨中横隔板、2个1／4跨主梁、1个1／2跨主梁）的局部梁段模型，并与轮胎模型进行全耦合，如图5所示。

图5 载重子午胎与沥青铺装层3D全耦合

局部梁段模型除力学响应敏感区之外，随着荷载距中心距离的增加，变形很快消失，所以对局部模型纵、横向及底部全部固结约束，即对四支座位置进行竖向约束，并选择一组对角支座进行横向约束，然后对另一对角支座进行纵向约束。但对加载于接缝处且均为中梁的工况，对两侧面约束横向自由度；而对加载于边梁翼缘处且含有一中梁的工况，只对中梁一侧约束横向自由度。在对端部设置横隔板的一跨混凝土箱梁桥1／4模型横隔板底部施加竖向和横向约束，对跨中横面、桥面中线纵面施加对称约束，相当于原桥面上切割1／4断面。

2 胎／面全耦合瞬态接触响应数值模拟与分析

2.1 胎／面全耦合响应分析工况数值化

轮胎的运动从滚动角速度ω与线速度v、滚动半径r的关系可分为自由滚动、加速驱动、减速制动3种工况，如图6所示。当r确定后，轮胎滚动工况便由ω与v的相对关系来确定。其中，自由半径rf指无负荷旋转轮胎的轮轴中心至胎面中心距离；滚动半径rG系轮胎滚动一周时轮胎中心水平移动距离与2π的比值，即rG＝v／ω，而自由滚动状态时称为有效滚动半径。

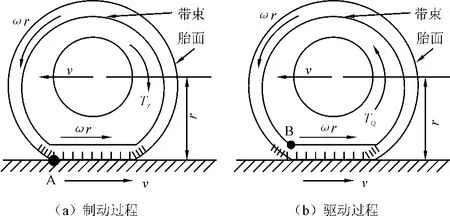
图6 制动与驱动工况下驱动轮角速度、车速状况

2.1.1 自由滚动

指轮胎没有外加驱动或制动扭矩，胎／面接触面上纵向切应力前后呈对称、反向分布的滚动状态，且自由滚动半径rkc（m）与轮胎平动线速度vc（m·s－1）、临界角速度ωc（rad·s－1）存在rkc＝vc／ωc的关系。

2.1.2 减速制动

如图6（a）所示，当对驱动轮施加制动扭矩Tz后，驱动轮将由匀速开始制动减速，直至制动力超过轮胎附着力时，驱动轮将出现极限滑移状态。制动时因施加制动力矩而使轮胎ω小于自由滚动条件下的角速度，其中Δv为轮胎与桥面的相对速度，即rω＜v且Δv＝v－rω。此时，接触面部分接触点开始滑动且出现部分制动。当所有接触点完全向后滑动时，将出现制动抱死。此时，驱动轮带束不动，桥面向后滑移，对于桥面上A点从接地面前端向后移动x距离需要的时间t及其相对位移Δx，有Δx＝Δvt＝（v－rω）t，如令t＝x／v，驱动轮滑移率Sc＝（v－rω）／v，则Δx＝Scx且Sc＞0。

2.1.3 加速驱动

如图6（b）所示，当对驱动轮施加驱动扭矩TQ后，直至驱动力超过轮胎附着力，驱动轮将出现空转。驱动过程中因施加驱动力矩而使轮胎ω大于自由滚动条件下的角速度，即rω＞v且Δv＝v－rω。此时，接触面间部分接触点开始滑动，且部分加速。当所有接触点完全向前滑动时，将出现完全加速。当空转时，驱动轮转动，而桥面则不动，对于桥面上B点从接地面前端向后移动x距离需要的时间t及其相对变位Δx，有Δx ＝Δvt＝（v－rω）t；如令t＝x／（rω），驱动轮滑移率Sb＝（v－rω）／（rω），则Δx＝Sbx且Sb＜0。

下面通过ABAQUS确定2种轮胎在不同v时的ωc及rkc，主要步骤如下。

（1）估算ωc。新胎自由半径rf近似rkc，可估算ωc，11R22.5胎在rkc≈rf＝0.532m、707kPa、25kN、f＝0.2、v＝16.666 7m·s－1时ωc＝31.328 4rad·s－1。425／65R22.5胎在rf＝0.563m、830kPa、50kN、f＝0.2、v＝16.666 7m·s－1时ωc＝29.603 4rad·s－1。

（2）求解切应力平衡解。在 ABAQUS／CAE Step模块中设置轮胎预压pre、充气inflation、荷载load模块及roll1，roll2，…，roll15共15个滚动分析步，且每个滚动步时间为0.002s（约大于1个单元长度所需时间）；在load模块通过边界条件在所有滚动步均对轮辋参考点施加纵向v＝16.666 7m·s－1边界，而在15个滚动步依次施加横向角速度模拟轮胎减速抱死、制动、自由滚动、驱动、加速空转5种工况。

最后，绘制如图7、8所示接触区中心节点处纵向切应力与ω的关系曲线，可见：当轮胎自由滚动时，胎／面接触切应力前后对称，且此时扭矩为0，即可求出临界角速度ωc，见表3。

由图7可知：当11R22.5驱动轮以10km·h－1滚动时，其ωc在0～4.5rad·s－1之间，胎面受到桥面的切应力几乎不变且方向为负（与行车同向）；达到4.5rad·s－1后切应力下降，直到5.5rad·s－1时接触区中心切应力接近于0，此时为自由滚动状态；超过5.5rad·s－1后切应力开始增大且改变方向（与行车反向），达到6.11rad·s－1后切应力又趋于稳定。

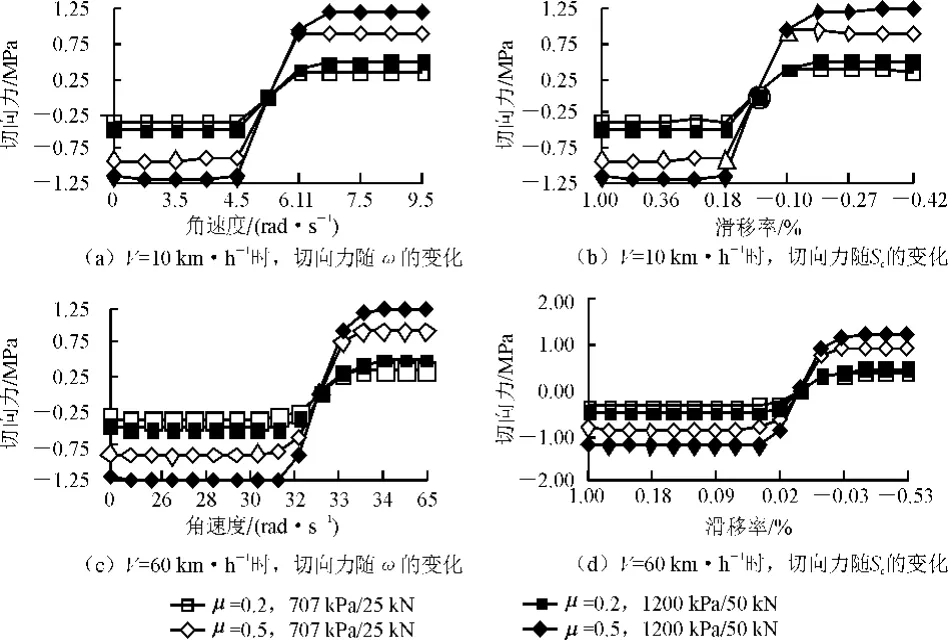
图7 不同条件下11R22.5胎纵向切应力随ω与Sc变化规律

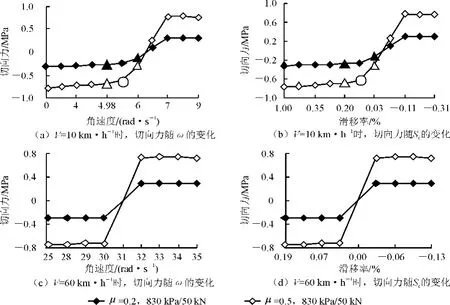
图8 不同条件下425／65R22.5胎纵切应力随ω与Sc变化规律

表3 不同速度下、不同轮胎、不同工况下的临界角速度结果

同时，切应力随滑移率S的变化规律与角速度类似，当S大于12%时轮胎制动抱死，12%＞S＞0时胎面前端黏结、后端滑移，而0＞S＞－12%时前端逐渐滑移，后端部分黏结；当S达到－12%时轮胎完全驱动空转。60km·h－1行驶时与低速类似，但ωc＝33rad·s－1时，发生制动抱死与驱动空转的滑移率范围更小了，约为－1%～1%，说明车速越高，轮胎制动、自由滚动、驱动工况更容易转化，这与现实中的汽车驾驶状况比较一致。另外，1 200kPa／50kN时上下2个峰值切应力对应的ωc约为2.5～9.5rad·s－1，而707kPa／25kN时则为3.85～8.5 rad·s－1，且切应力普遍增加150%，说明重载、超压下工况转化更难，而附着系数对于工况转换影响不大，对切应力影响较显著。

图8表明：对于425／65R22.5宽基单胎来说，10km·h－1与60km·h－1速度下行驶时ωc分别为6.2rad·s－1和31rad·s－1，但低速时Sc为－10%～10%，说明低速时宽基胎比窄胎更易转换；而高速时Sc约为－2%～2%，反而比窄胎更迟钝。在相同车速、附着系数、胎压／轮载组合下，3种工况转换时的宽基胎瞬态切向应力最高为0.748MPa，而窄胎则比宽基胎则高出40%，说明宽基胎对桥面耐久性更为有利。

2.2 侧偏工况下胎／面全耦合瞬态接触响应模拟

当汽车行驶在弯道或在直道上转弯时，由于克服离心力作用而对轮胎施加回正力矩，从而使轮胎在桥面上发生侧偏现象，且以侧偏角α边滚边滑，桥面将对接触面产生与其转弯同向的侧偏力，提供保证车辆平稳转弯的向心力。

在有限元模拟中，由速度边界条件来定义不同车速的侧偏工况。将实际车速分解为vx及vy。对于某一固定速度vx，便可通过变化侧偏角α获得vy，也就得到了对应于不同α的有限元速度边界条件组合。

式中：vx为汽车纵向速度；vy为汽车径向速度。

本文取vx分别为10km·h－1和60km·h－1，α取1°～15°（间隔1°），对11R22.5胎（707kPa／25kN、1 200kPa／25kN）分别在制动抱死、自由滚动、驱动空转3种工况下的侧偏工况进行模拟，接触区内外侧接触压强如图9所示，胎／面侧向应力见图10。

图9表明：当侧偏角从1°增加到15°时，胎面接触区的压强中心区从侧偏内侧逐渐向外侧移动。由图10可知：制动抱死、驱动空转工况下的侧向力在侧偏角为1°～3°时均在行车纵向中段出现了负值，说明侧偏角较小时胎／面接触区前部、后部各自先发生回转，导致侧向力2次变向。而当α增大时，2个回转中心逐渐向轮胎中部靠拢直至重合，此时轮胎底部整体向外侧滑。另外，制动抱死时负侧向力峰值出现在接触区前部，且正侧向力也在接触区前部较大，而驱动时负侧向力峰值出现在后部，且正侧向力也在后部偏大，这与制动、驱动模拟结果十分吻合。对于自由滚动工况，从图10中可见发生接触区整体侧滑的侧偏角较大，约为6°以上，当侧偏角增加到15°时，侧偏力提高了10倍，最大值可达1.39 MPa。该模型计算时采用的摩擦系数为0.2，而如果采用μ＝0.8计算，则侧偏力提高近30倍，这充分说明小半径弯桥上轮胎将发生侧滑。

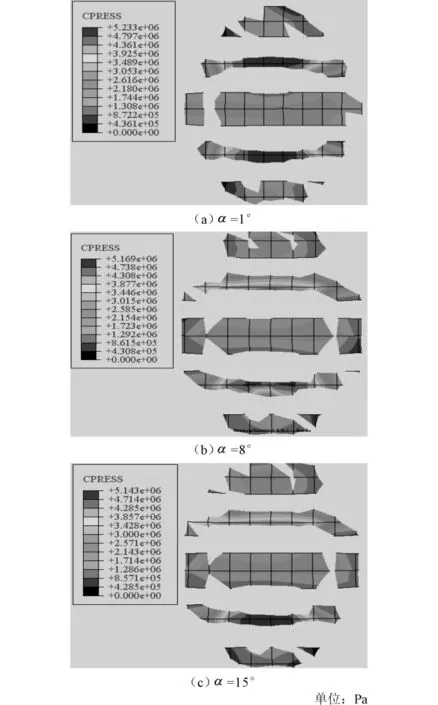
图9 不同侧偏角时胎／面接触区由内向外压强变化

因此，当轮胎制动或驱动加速时，接触区横向中部均滞后于边缘（左右端），易导致桥面发生“U”型开裂，而侧滑时纵向中部却滞后于前后边缘，扭转剪切将加剧桥面的非对称“U”型变形。

2.3 侧压工况下胎／面全耦合接触响应模拟

2.3.1 胎／面接触形状模拟

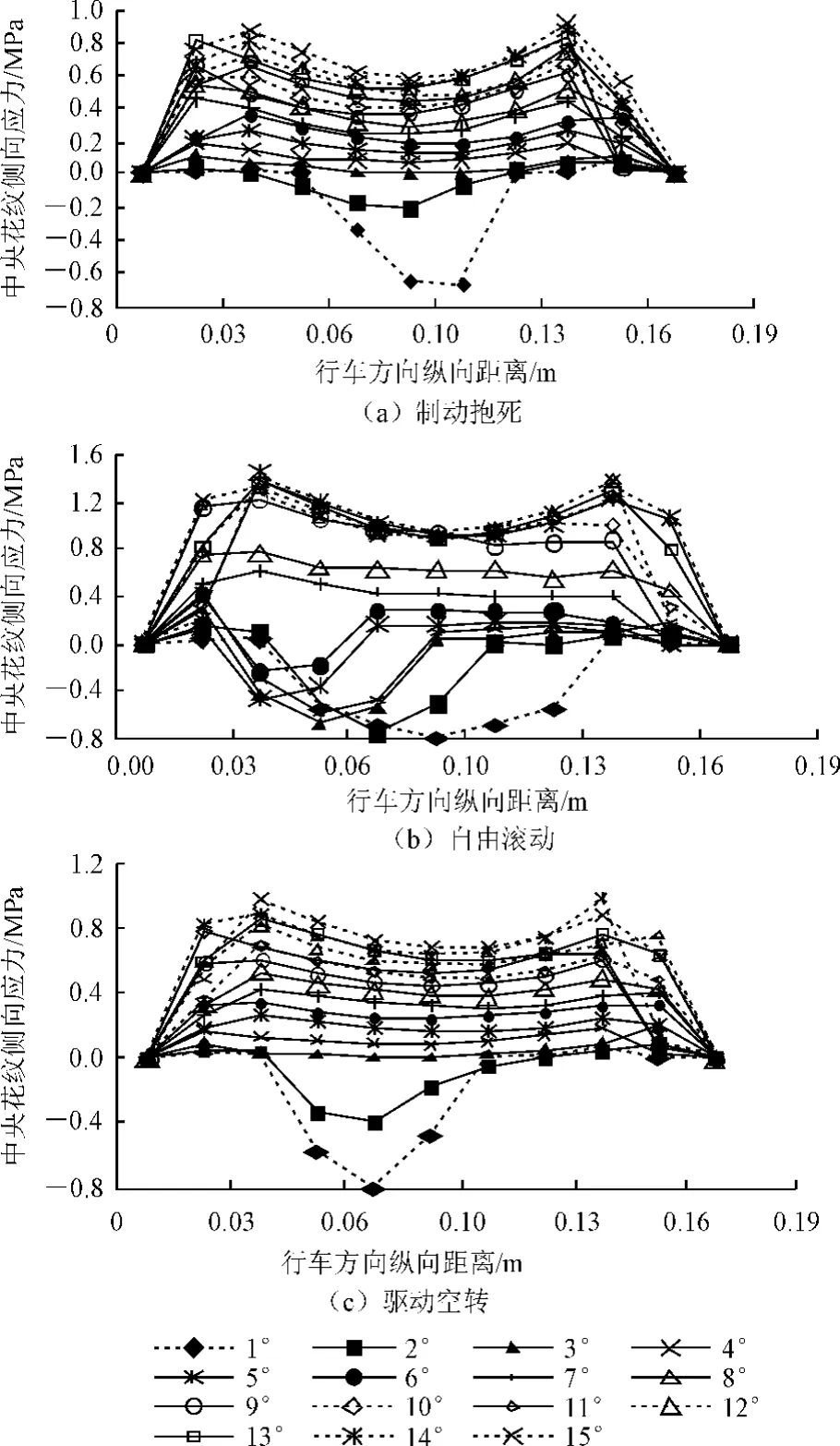
图10 不同工况及不同侧偏角下侧偏力变化

当汽车在严重车辙的桥面辙槽内侧、弯坡桥超高侧行驶以及转弯有侧翻趋势时，轮胎外边缘将发生侧向局部受压，即“侧压”。选择最大横坡度为6%分别对11R22.5胎与425／65R22.5宽基胎在不同条件下的胎面接触区应力分布与胎面接触区变形状态进行模拟，如图11～14所示。

由图11、12可知：11R22.5胎在侧压工况707kPa胎压下，随着轮载的增加，受压一侧逐渐由椭圆形向矩形发展，而抬起一侧则维持半圆，接触压强中心也从中央花纹处向受压一侧移动，但其横向接触面面积比纵向增大速度快。

由图13、14可知：425／65R22.5宽基胎胎／面接触区面积纵向比横向扩展速度快。总体来看，与非侧压工况相比，胎／面接触区最大竖向应力、最大横向应力、最大纵向应力分别增加33.3%、50%、16.6%。由此可见：侧压工况对于桥面铺装层的路用性能影响极大。

不同胎压下2种轮胎胎面接触面积随荷载的变化规律如图15、16所示（L为水平；S为横坡）。

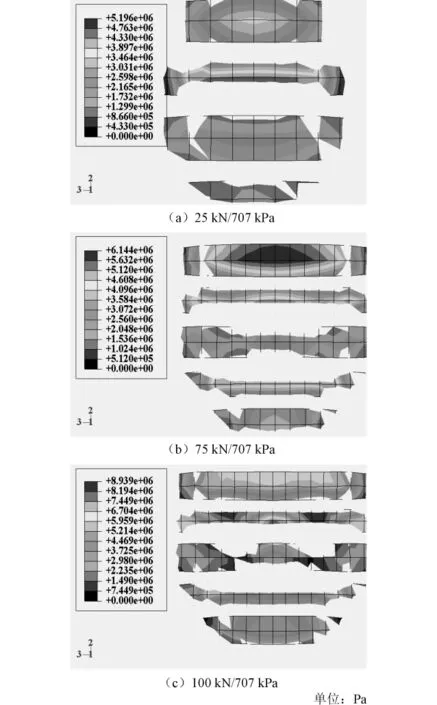
图11 不同条件下11R22.5胎／面接触区应力云图

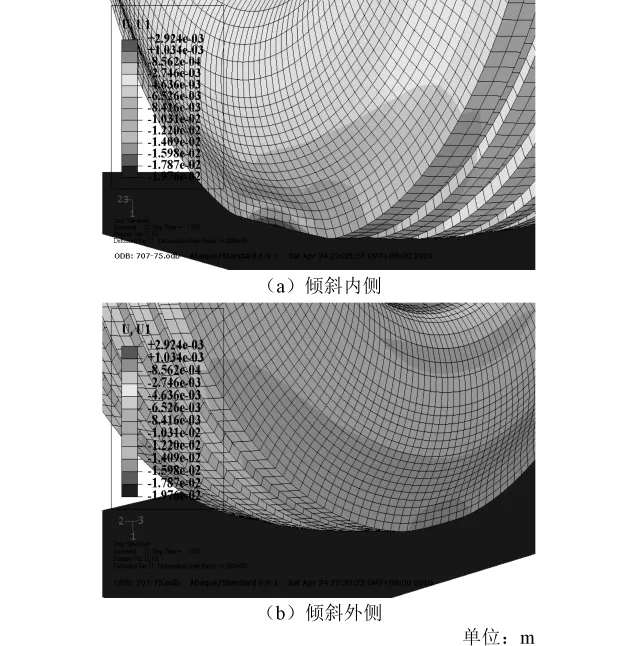
图12 不同条件下11R22.5胎／面接触区变形

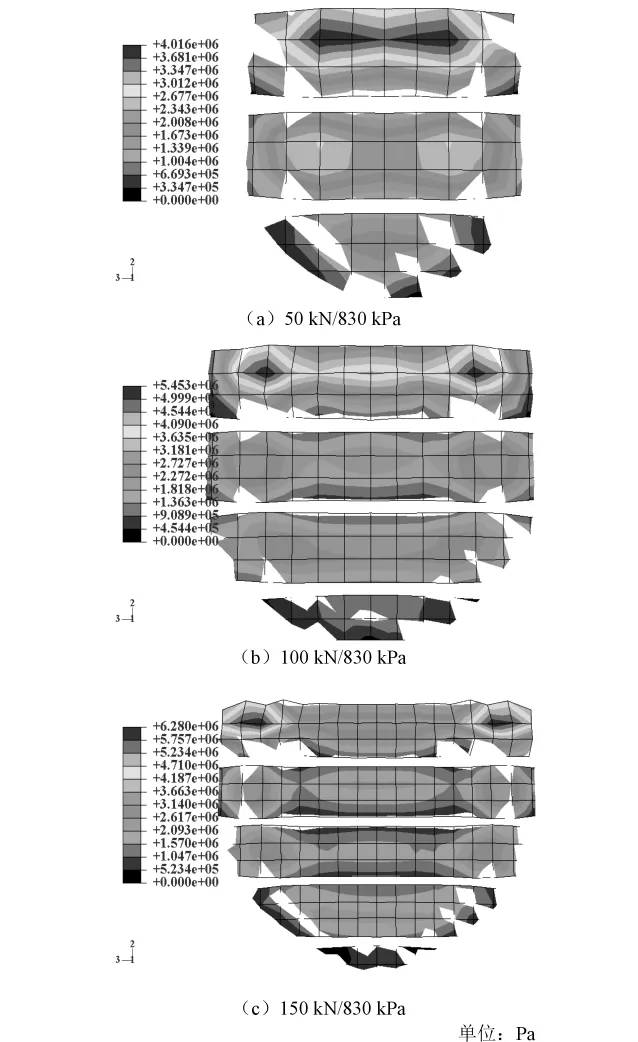
图13 不同条件下425／65R22.5胎／面接触区应力云图

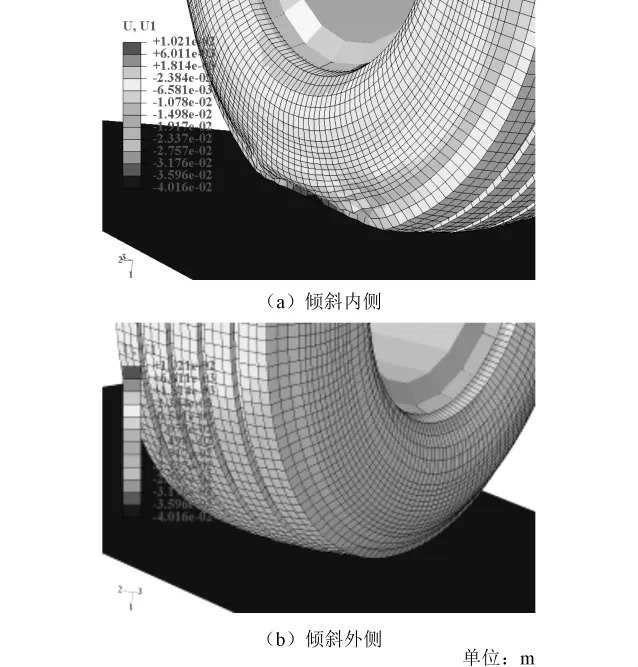
图14 不同条件下425／65R22.5胎／面接触区变形

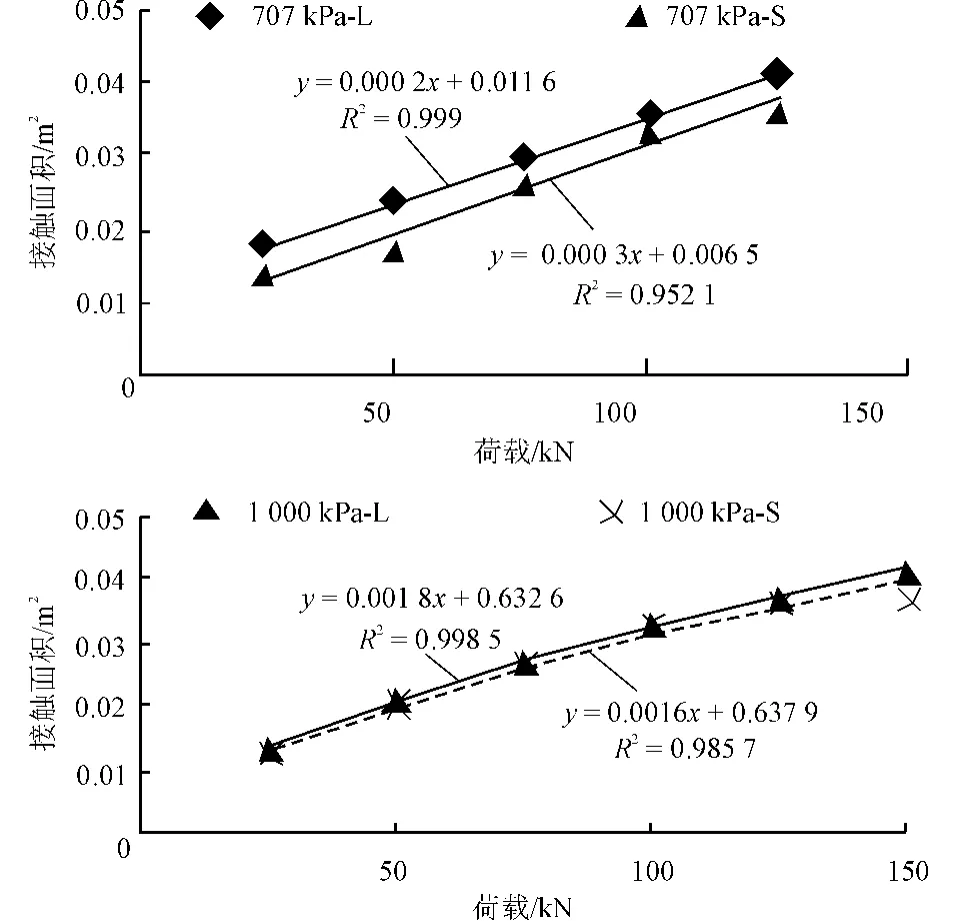
图15 不同胎压下侧倾时11R22.5胎／面接触面积与荷载的关系

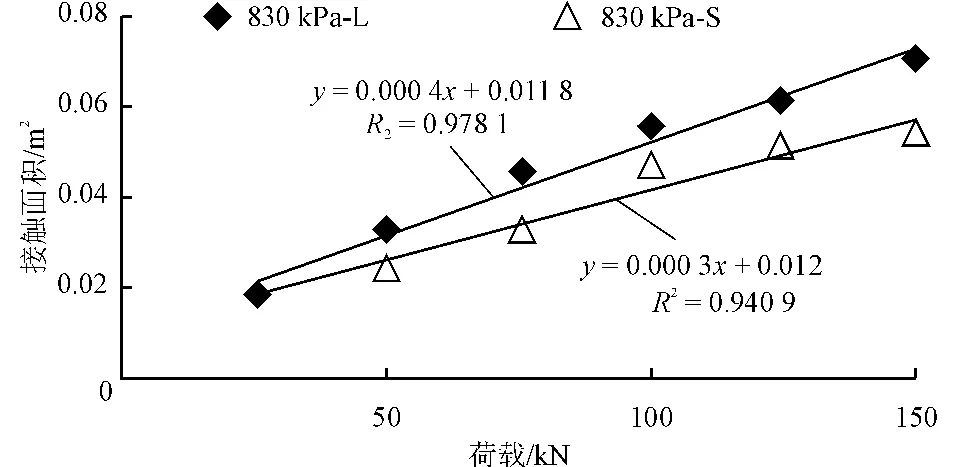
图16 不同胎压下横坡度为6%时425胎面接触面积与荷载的关系

对于11R22.5胎，在低胎压时接触面积A随荷载呈线性增长，而当胎压超过1 000kPa时，则呈幂函数增长，说明此时接触应力将显著增加；同时，不论荷载大小，侧压时接触面积与水平碾压时呈同幅度下降。图16则表明：在标准胎压下425宽基胎接触面积增长速率几乎与11R22.5胎相当，斜率约为0.000 3，且轻载时接触面积几乎相同；而随着荷载增加，侧压后的接触面积将显著增加。

2.3.2 胎／面接触应力及其分布函数

不同荷载、胎压组合下的胎／面竖向接触应力分布与水平碾压时基本一样，如图17、18所示。

由图19（a）表明：竖向应力在横向呈式（2）所示的3次多项式函数分布。

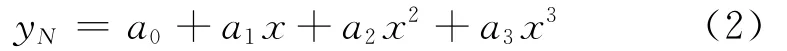
式中：a0＝0.09；a1＝261.5；a2＝－5638.5；a3＝30 053.5。

横向应力在横向则呈如图19（b）所示的振荡函数分布，由受压侧向抬起侧逐渐呈衰减趋势。

3 结 语

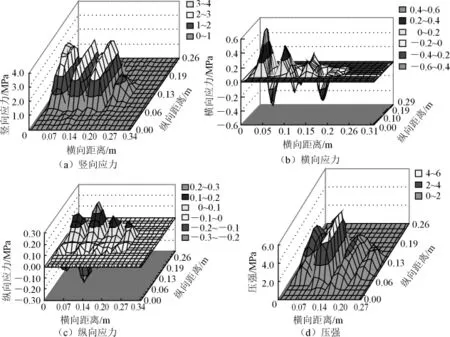
图17 横坡为10%时707kPa／25kN下11R22.5胎／面侧压响应

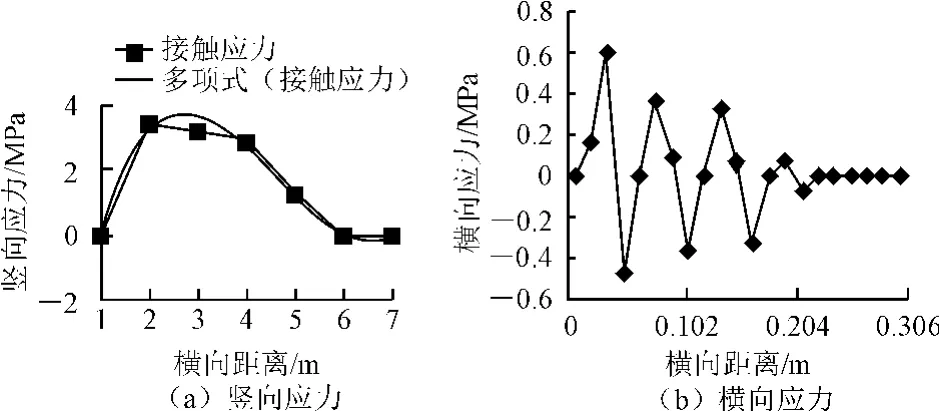
图19 应力沿横向分布形态函数

（1）通过ABAQUS有限元软件对载重子午胎与桥面全耦合瞬态接触响应数值模拟发现：接触面上的竖向、横向、纵向应力分布形态、大小与水平行驶时的接触响应显著不同。

（2）低胎压、轻载下制动时轮胎前缘竖向应力、纵向应力较大，而驱动时相反，并随着胎压、轮载提高，竖向应力和纵向应力在纵向更为均布，425宽基胎的竖向应力、纵向应力比11R22.5胎更为均布，但比静载时分别高出12.5%、66.6%。

（3）当侧偏角较小即刚侧偏时，横、纵向接触应力发生复杂变化，当侧偏角超过3°～5°时接触应力趋于稳定向外侧；侧压工况下竖向应力在横向呈三次多项式分布，而横向切应力则呈振荡曲线分布，随着远离侧压段而振荡式衰减；在轻载／低压工况下，11R22.5胎侧压竖向应力增加18.5%，而重载／高压工况下则增加10.2%，说明重载／高胎压时侧压使接触应力更均布；而425胎竖向应力在轻载／低压时增加17.8%，而重载／高压下增加23.3%，说明宽基胎在弯道超高段、车辙辙槽内行驶时更为不利，且对近表面拉应力及整个结构层厚度内剪应力影响均较传统窄胎显著。