非线性最优化在斜拉桥索塔锚固区配束上的应用

向律楷, 鄢 勇, 艾宗良, 童登国

(中铁二院工程集团有限责任公司，四川成都 610031)

1 概述

斜拉桥索塔上拉索的锚固构造是将拉索的局部集中力安全、均匀地传递到塔柱全截面的关键构造。索塔锚固形式的采用要综合考虑许多因素：拉索的布置(如稀索、密索、单索面、双索面、拉索的构造等)、索塔的截面形式与构造、拉索锚具形式、拉索索力的大小、拉索的张拉工具与方法、梁上张拉还是塔上张拉，以及索塔的材料等等，故应从设计、施工、养护维修及拉索的更换等各个方面来综合考虑拉索锚固段的合理构造。

由于斜拉桥上塔柱拉索锚固区是斜拉桥的关键部位。随着斜拉桥的发展，工程师对索塔锚固区的构造进行了不断的探索实践，具体主要有以下四类锚固构造：拉索在塔柱上交叉锚固，在空心塔柱上设置环向预应力锚固，采用钢锚固梁对称锚固；利用钢锚箱对称锚固。

斜拉桥索塔锚固结构的类型，与斜拉索布置、斜拉索的根数和形状、塔形与构造、斜拉索的牵引和张拉、设计计算的可靠性、施工的可操作性、养护维修的方便程度等因素有关，故应从设计、施工、养护维修及斜拉索的更换等各方面综合考虑索塔锚固结构的选型。索塔锚固结构应该选用计算分析可靠、受力明确、构造简单、施工方便、养护维修方便的结构。

由于设置环向预应力锚固有对索面及塔内空间无特殊要求，造价低，后期维护工作量小，施工工艺成熟，所以大部分桥塔的都采用环向预应力锚固方案。传力机理为环向的平面预应力作为外力来平衡拉索锚固力产生的内力，以防止混凝土塔在拉索锚固力作用下开裂。

但是，由于索塔锚固区的斜拉索数量很多，斜拉索的索力不一致，间距不相等，角度不相同，造成索塔锚固区不同部位的受力状态显著不同，相应的环向预应力钢束的布置也应有所区别。若环向预应力的配置采用统一的方案或将导致索塔锚固区应力分布不合理，不同位置的混凝土拉、压应力将导致混凝土局部开裂或者压溃，影响桥塔结构的耐久性乃至结构的安全；或又将导致部分区段的环向预应力布置过多，不合理，经济性欠佳。

传统的设计方法，一般通过试算的办法来进行设计，需要计算的次数多、效率低、设计周期长，而且环向预应力钢束的配置也不够精准，一般会造成不同程度的浪费。

2 最优化模型

首先，建立有限元模型，求得单位面积钢束以及单位力对桥塔产生的应力，即应力系数矩阵。截取1 m厚的桥塔，建立平面有限元模型，将斜拉索的水平分力除以斜拉索的间距，得到施加在模型上的力；根据以往的经验，初步配置环向预应力，根据工程实际设定预应力钢束的永存应力，并假定配置的钢束面积，以此作为单位面积。求解，得到单位斜拉索索力及单位面积预应力钢束对桥塔产生的应力，即应力系数矩阵。

其次，建立最优化数学模型。为了建立最优化方程，设同一根拉索处有n根预应力钢束。若每根钢束的面积为单位面积，产生的正面内侧和外侧正应力为σzni、σzwi(i=1,2,……,n)，侧面内侧和外侧应力为σcni、σcwi(i=1,2,……,n)；正面内、外侧以及侧面内、外侧的正应力为σzn、σzw、σcn、σcw。单位索力对正面内外侧，侧面内外侧产生的应力为σfzn、σfzw、σfcn、σfcw。假设任一种配束方案中钢束面积及荷载分别为ai(i=1,2,……,n),f。根据叠加原理，施工阶段(即只张拉预应力钢束，还未张拉斜拉索时)的应力为

主力工况下应力为

下面建立最优化方程，设施工阶段内侧、外侧正应力分别小于[σsn],[σsw]，主力阶段内侧、外侧正应力分别小于[σzn],[σzw]，则

目标函数minobj=(σzn-σzw)2+(σcn-σcw)2

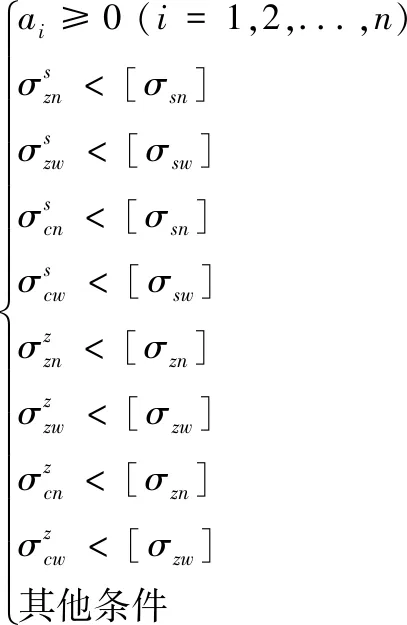
其中，其他条件可以根据工程上的需要任意设置。

根据上述方程求解，如果有可行性最优解，则表明前面假设的预应力方案是合理的，进而得到理论上的最优预应力配置方案。如果无最优解，则表明前面假设的预应力方案不合理，需要重新假设。

3 算例

本文以主跨432 m的某铁路大跨度斜拉桥桥塔索塔锚固区环向预应力钢束为例，对文中所述方法进行分析。

3.1 索塔锚固区基本构造介绍

该桥塔采用钢筋混凝土H型桥塔，塔高188 m，由上、中、下塔柱组成，分别设置了上横梁和下横梁，其中索塔锚固区高58 m，共设置14对斜拉索。索塔锚固区采用环向预应力锚固方案，如图1所示。

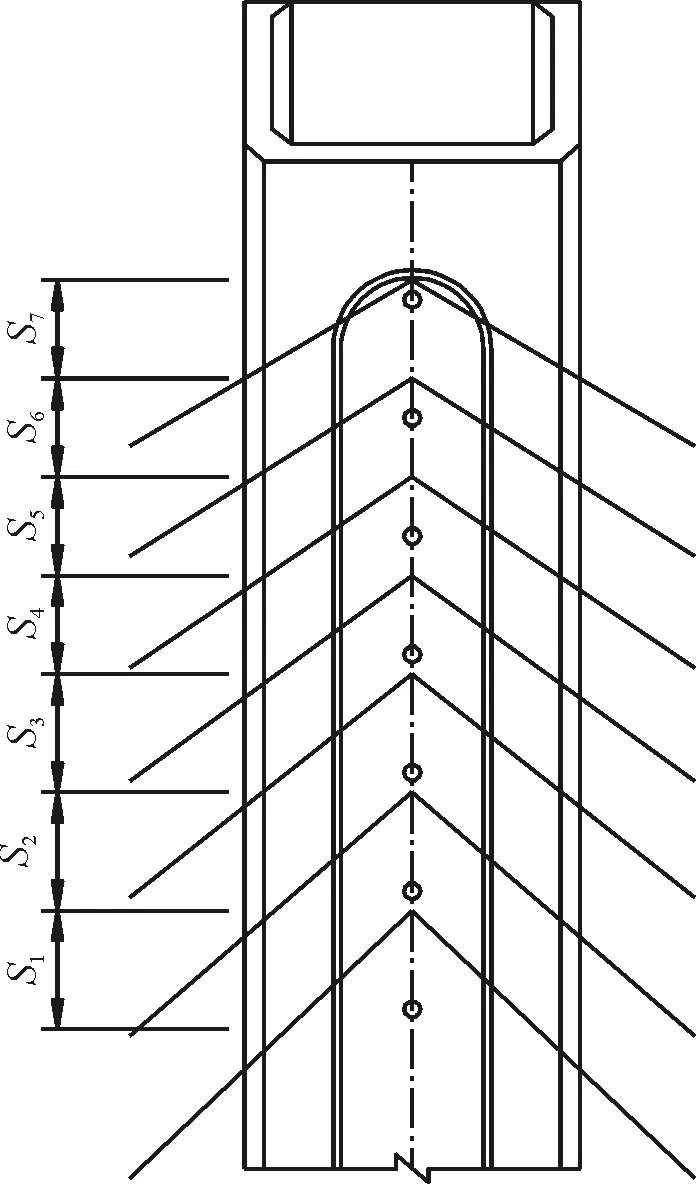
(a)索塔锚固区立面

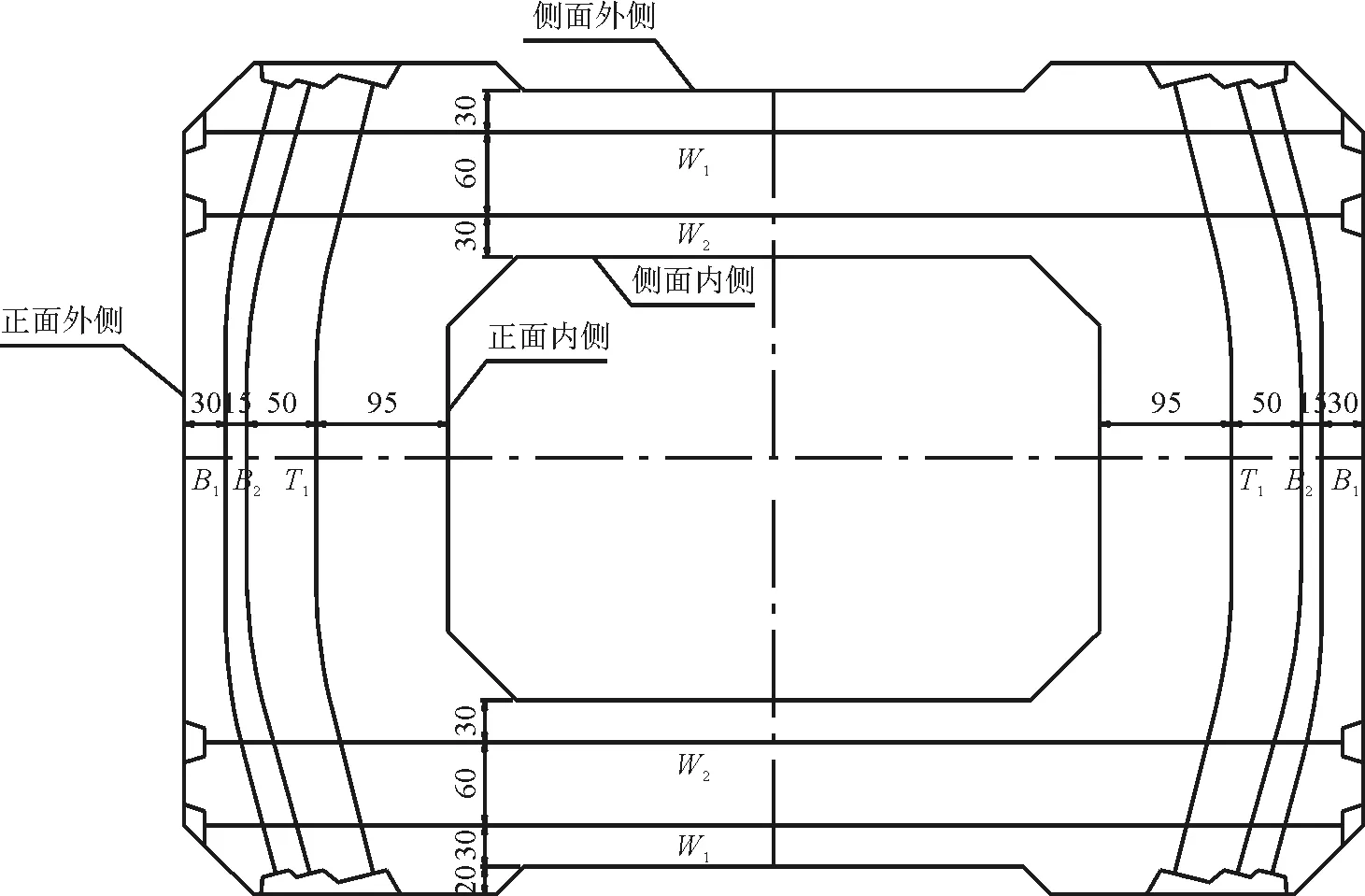
(b)索塔锚固区断面图1 桥塔S1-S7段构造及配束示意

本文仅考虑桥塔索塔锚固区顶部的7个节段，每个断面配置了5根钢束T1、B1、B2、W1、W2。预应力钢束采用7Φ15.2 mm的钢绞线，抗拉强度标准值为1 860 MPa，张拉控制应力为1 209 MPa。

3.2 应力系数矩阵计算

由于索塔锚固区受力复杂，有必要对其进行实体分析。由于本桥采用井字形配筋方式，索塔锚固区分析最重要的作用是为了合理配置预应力钢束。综上，分析时采用平面模型。

为了减少计算量，根据对称性，取四分之一模型进行分析。对混凝土采用2D 8节点平面应力单元plane82(经过计算用平面应变单元结果基本一致)，预应力钢束采用杆单元link8。为了在全塔合理配置预应力钢束，对每一个节段都进行计算。计算时在竖向取1 m长，即板厚1 m。有限元模型如图2所示。

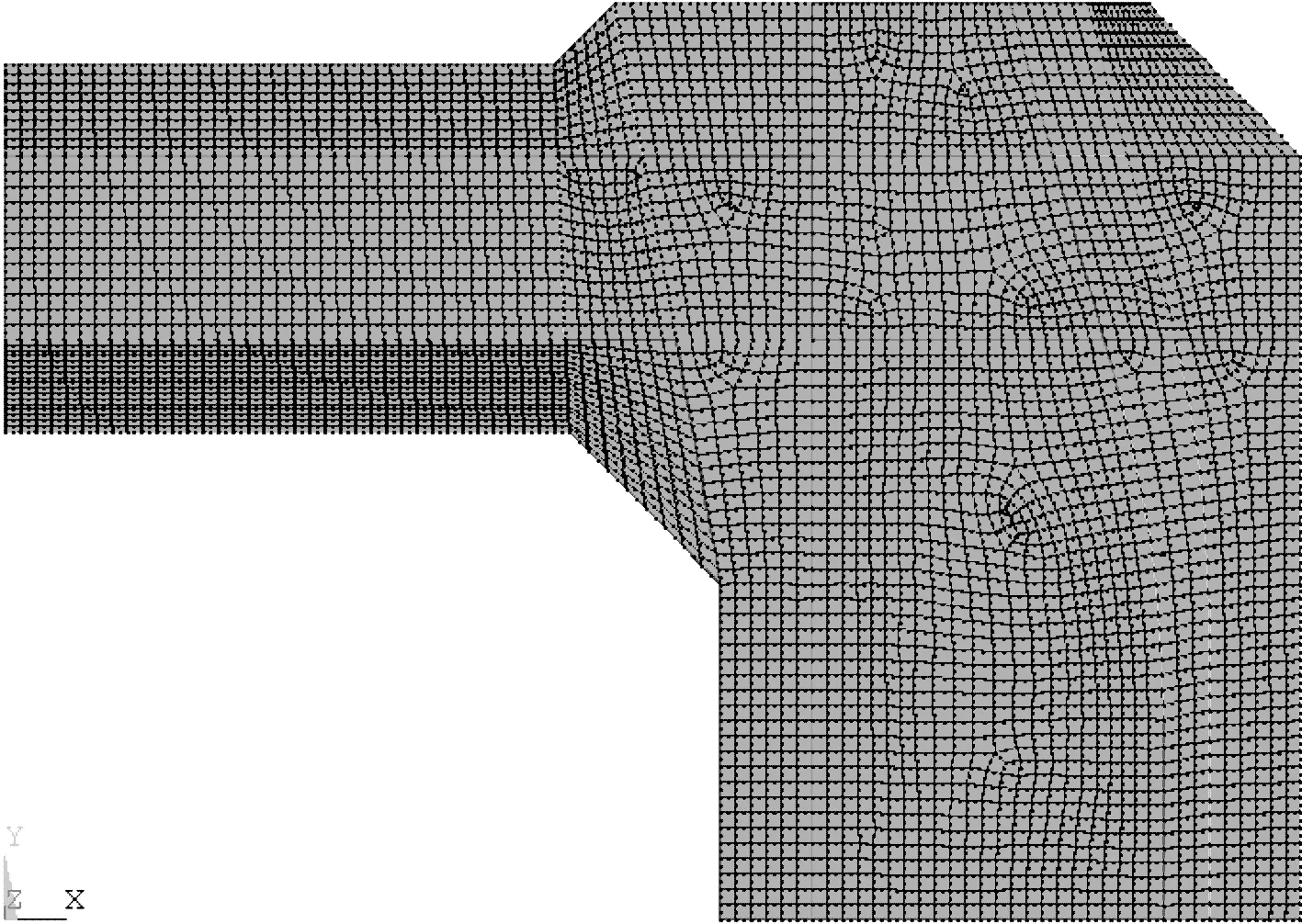
图2 有限元模型

根据有限元模型得到的结果如表1所示。

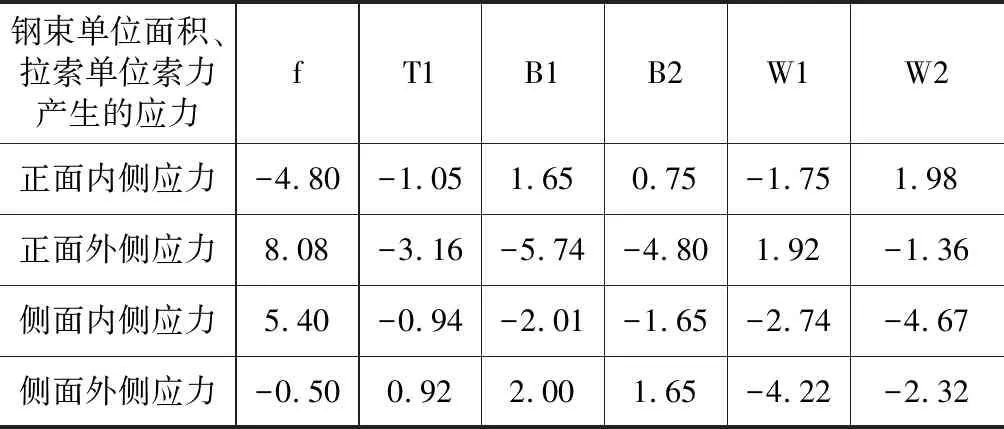
表1 单位面积钢束及单位索力产生的应力 MPa

注意，表中钢束单位面积为140×7×4=3920mm2，拉索单位索力为3 051 kN。根据表中数据，按照叠加原因，可以非常方便的计算任一配束方式下的应力。为了方便，不妨称为单位面积钢束及单位索力产生的应力为应力系数矩阵。

3.3 最优化配束计算

本桥索塔锚固区按照部分预应力A类构件(及允许出现拉应力但不开裂)设计，根据TB 10002.3-2005《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》6.3.11第2条

0.7fct=0.7×3.10MPa=2.17MPa

所以施工阶段，取[σsw]=2.17MPa，[σsn]=2.17MPa。

又因为寒潮对结构产生约3 MPa的拉应力，所以主力工况下，[σzw]=2.17-3=-0.83MPa，整体升降温影响很小，所以不考虑。为了留一定的安全储备，外侧取[σzw]=-1.1MPa，由于寒潮作用深度到达不了内侧，应力限制条件不用取得与外侧一样严格，所以取[σzn]=-0.5。

对于上部配束方式，约束条件中的其他约束条件，根据工程需要，可以如下式设定

a1=a2=a3=a4=a5

将表1中的数据代入式最优化方程得到最优化配束结果，如表2所示。

4 结 论

本文首先建立有限元模型，得到应力系数矩阵。然后建立非线性最优化数学模型，求解得到合理的索塔锚固区配束面积。最后通过实例，得到了可靠的索塔锚固区配束面积，证明了该方法的正确性及可行性，并且直接应用于432 m主跨的斜拉桥设计中，该桥目前已开通运营，运行效果良好。本方法只需要建立一个节段的平面有限元模型，大大减小了由表2中所得的数字乘以钢束单位面积即可得到最终的配束面积。

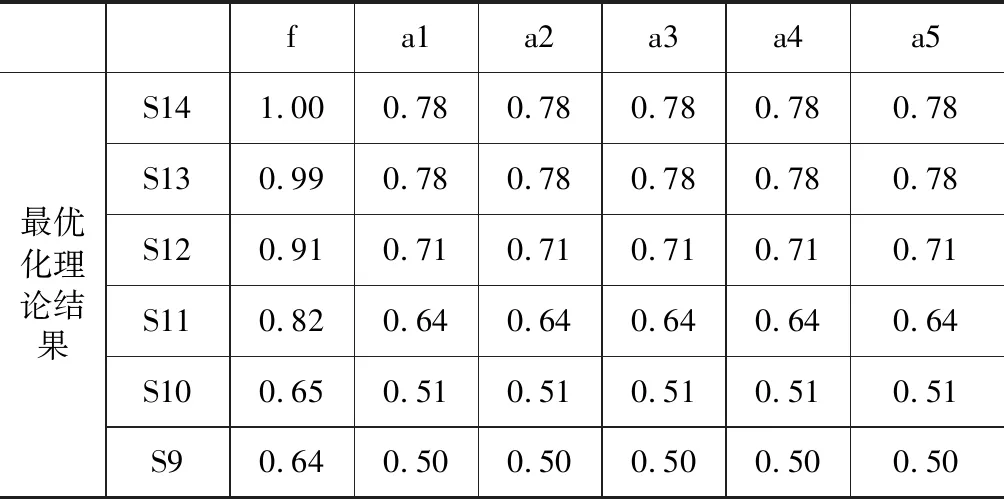
表2 最优化配束结果

计算工作量，且不用试算，直接根据最优化理论求解，大大加快了设计的速度。能够使得桥塔索塔锚固区的不同拉索位置处的应力处于相同的水平，不仅能够更好的保证结构的耐久性和安全性，而且能够节省混凝土及预应力钢束的材料。