调和数相关恒等式的计算机辅助证明

温新奇，靳海涛

（天津职业技术师范大学理学院，天津 300222）

组合恒等式的证明和发现是组合数学的一个重要研究课题，其传统证明方法灵活多变，往往涉及代数、组合、分析等数学分支。近些年来，计算机代数方法的兴起使得组合恒等式的证明有了革命性突破。需要特别指出的是，研究人员利用Gosper 算法和Zeilberger 算法[1]，可以证明绝大多数的超几何恒等式。然而，组合数学中存在大量的非超几何序列，因此其相关恒等式的证明正成为当下研究的热点。研究表明，处理非超几何和式的一个基本思路就是将其转化为超几何项，例如文献[2]中采用Newton-Andrews方法将调和数转化为超几何项，文献[3]利用围道积分将Bernoulli 数转化为超几何项。

调和数是一类经典的非超几何组合序列，在算法分析、数论以及量子物理学等领域中发挥着重要作用。此外，调和数的相关恒等式的研究也引起研究人员的广泛关注。例如文献[4]通过一个含有调和数的恒等式证明了著名的Beukers 猜想，文献[5]研究了含有调和数的Euler 和，并给出了大量无穷和等式。因此，给出证明和发现含有调和数的相关恒等式的系统化方法具有重要的理论和应用价值。目前的方法主要包括计算机代数方法[2]、部分分式分解[6]、Riordan 群[7]和求导算子[8-9]等。本文利用形式留数算子[10]给出了调和数的一个超几何表示[11]，将调和数的相关求和问题转化为超几何求和问题，进而利用经典的Gosper 算法和Zeilberger 算法处理相应和式，最后通过取留数得到原始和式的相应结果。

1 基础知识

1.1 形式留数算子

定义对其形式留数定义为resz（f（z））：=z-1f（z）=a-1。

性质对给定的有resz（kf（z）+tg（z））=kresz（f（z））+tresz（g（z））。

1.2 调和数Hn的超几何表示

由于调和数是非超几何项（即Hn+1/Hn不是关于n的有理函数），因此处理相关和式的核心是给出调和数的超几何表示。一个经典方法是考虑函数f（x）=利用微积分知识不难证明Hn=f′（0）。文献[2，9]就利用该超几何表示证明和发现含有调和数的相关恒等式。

对非负整数n，记

本文利用该函数给出了调和数的另一个超几何表示。

性质H（n，x）是关于 n 的超几何项，并有

证明

1.3 Gosper算法和Zeilberger算法

Gosper 算法和Zeilberger 算法是处理超几何项和式的2 个经典算法，其具体计算步骤和历史发展可见文献[1]。

（1）Gosper 算法完全解决了超几何项的不定和问题。考虑不定和式其中，tk为一个超几何项。Gosper 算法将寻找一个超几何项zk，使得tk=Δkzk=zk+1- zk。若算法成功，则给出zk，进一步对k 求和可得Sn=zn+1-z0；若算法失败，则表明tk不存在超几何不定和。

（2）Zeilberger 算法用来处理双超几何项的定和问题。考虑和式其中，F（n，k）为关于n，k 的超几何项。Zeilberger 算法将寻找与k 无关的一些多项a0（n），a1（n），…，aJ（n）式和一个有理函数R（n，k），满足如下斜递推关系：

一般地，记 G（n，k）=R（n，k）F（n，k）。进一步，式（2）两边对k 求和可得到和式f（n）满足的一个递推关系式。为证明恒等式f（n）=T（n），只需验证T（n）满足该递推关系，且与f（n）具有相同的初值即可。

2 调和数相关恒等式的证明

给定一个含有调和数的相关和式，基本思路如下：

（1）将求和项代换为对应的超几何项表示，从而变为超几何和式。

（2）利用Gosper 算法或Zeilberger 算法，得到对应超几何项的不定和或斜递推关系式。

（3）对所得的不定和或斜递推关系式取形式留数并对k 求和，即可得到相关恒等式或和式满足的递推关系式。

一般情况下，对定和等式只需验证恒等式右端也满足同一递推关系式，且取相同的初值即可。

2.1 Gosper算法的应用

利用Gosper 算法给出几个已知恒等式的新证明。

例1证明经典著作[12]中的如下反演公式：

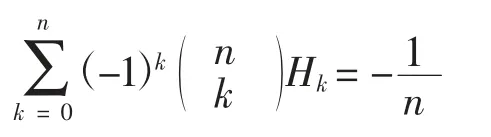
证明记求和项为tk，并记x）。由 Gosper 算法可得：

利用式（1）并注意到：

对式（3）两边取留数可得：

进一步，对k从0到n求和，即得：

例2证明如下恒等式：

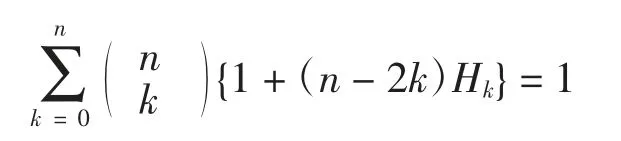
Garvan 首先给出了该恒等式的猜想[13]，Paule 和Schneider 在文献[2]中利用Sigma 软件包证明了该猜想，Chu 和Donno 在文献[8]利用超几何级数重新证明了该等式。

证明记求和项为tk，记x），由 Gosper 算法可得：

化简可得：

例3计算和式

解记求和项为 tk，记 Tk=kH（k，x），由 Gosper 算法可得：

利用式（1）并注意到：

对式（4）两边取留数可得：

将上式两边对k 求和得：

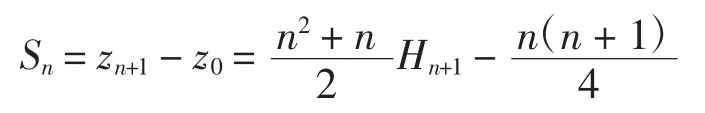
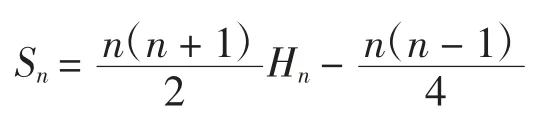
例4计算和式

解记求和项为 tk，并记 Tk=k2H（k，x），由Gosper算法可得：

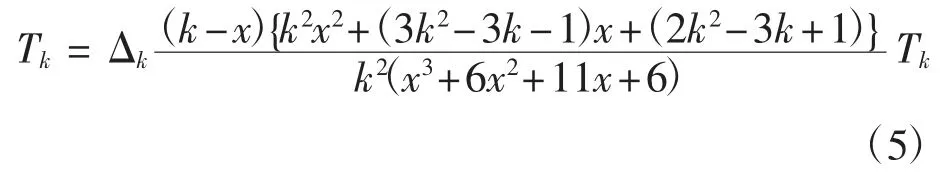
利用式（1）并注意到：

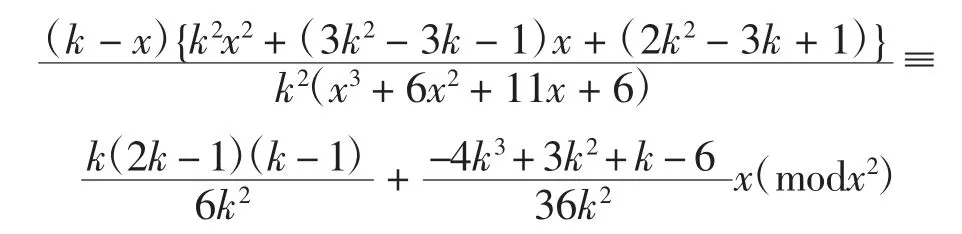
对式（5）两边取留数可得：

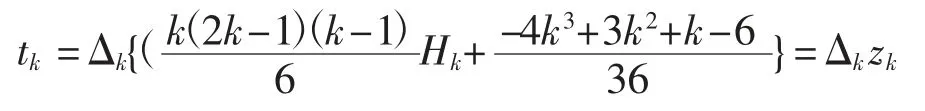
上式两边对k 求和可得：

同理，上式可整理为：

2.2 Zeilberger算法的应用

利用Zeilberger 算法给出几个已知恒等式的新证明。

例5证明如下恒等式：

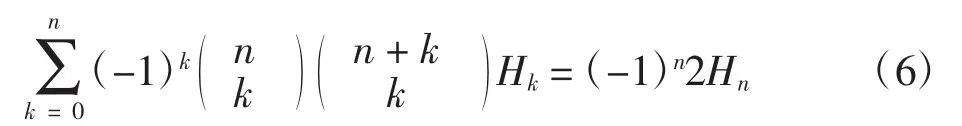
Prodinger[6]利用部分分式分解给出了该恒等式。之后，Osburn 等[15]利用计算机代数包Sigma 重新证明了上式。

证明记左端和式为f（n），并记F（n，k）=（-1）k·，由 Zeilberger 算法可得：

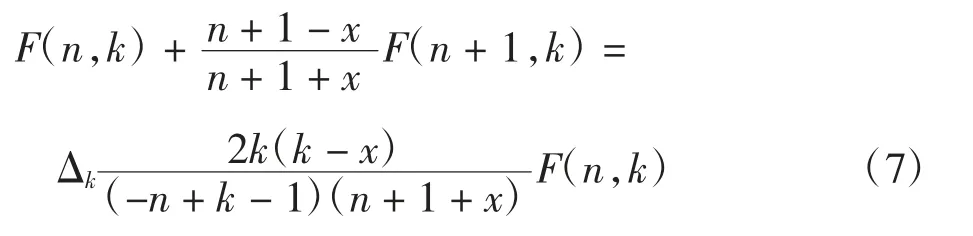
利用式（1）并注意到：

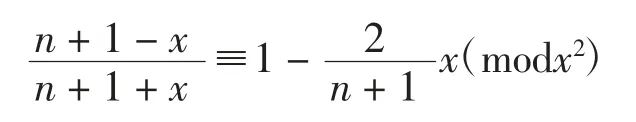
对式（7）取留数并对k 求和可得：

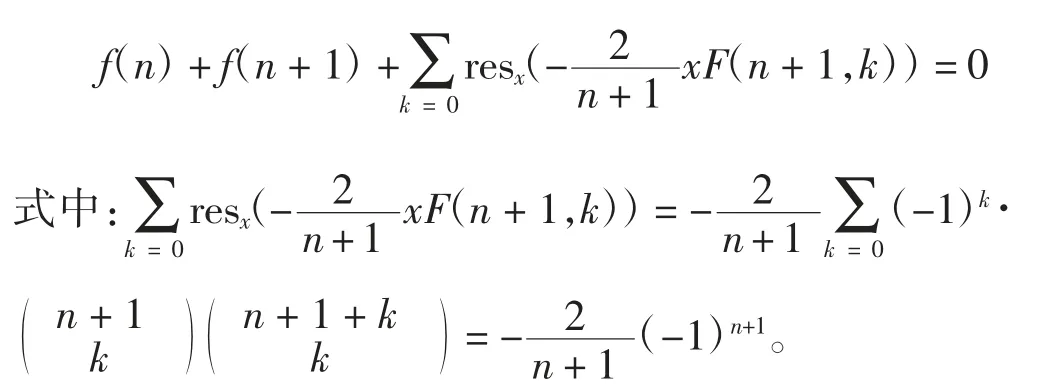
于是，可得f（n）满足递推关系：

可以验证式（6）右端也满足上述关系且与f（n）有相同初值，故恒等式成立。

例6证明如下恒等式：

Paule 等[2]利用计算机代数包Sigma 发现并证明了该恒等式，文献[11]利用Abel-Zeilberger 算法也给出了证明。

证明要证上式成立，即证：

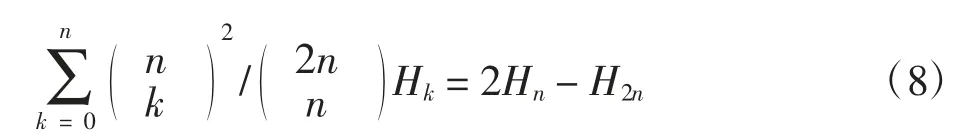
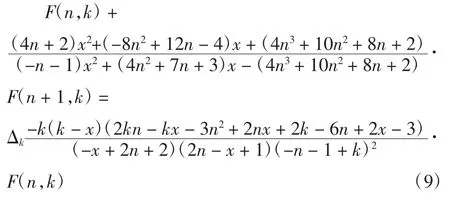
注意到在式（9）中：

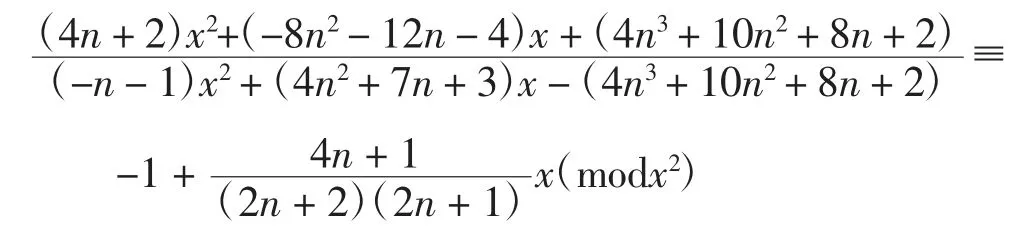
根据式（1），对式（9）取留数并对 k 求和可得：

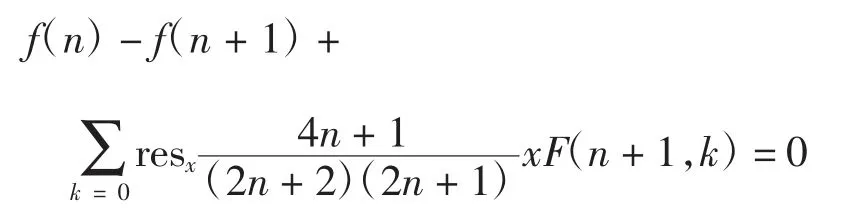
注意到其中：

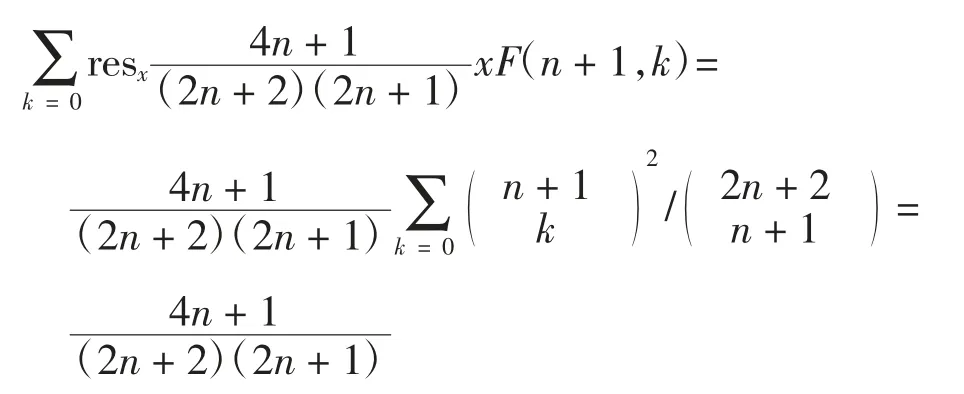
即可得f（n）满足递推关系式为：

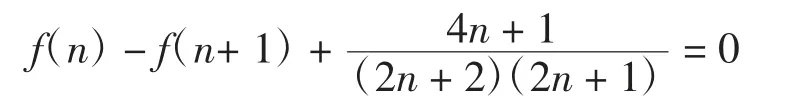
可以验证式（8）右端也满足上述关系且与f（n）有相同初值，故恒等式成立。

例7证明如下恒等式：

文献[2]首先证明了该恒等式，文献[9]重新给出了证明。

证明当n=0 时，上式左右两边均等于1，该恒等式成立。

下面考虑n ＞0 的情形。

式中：

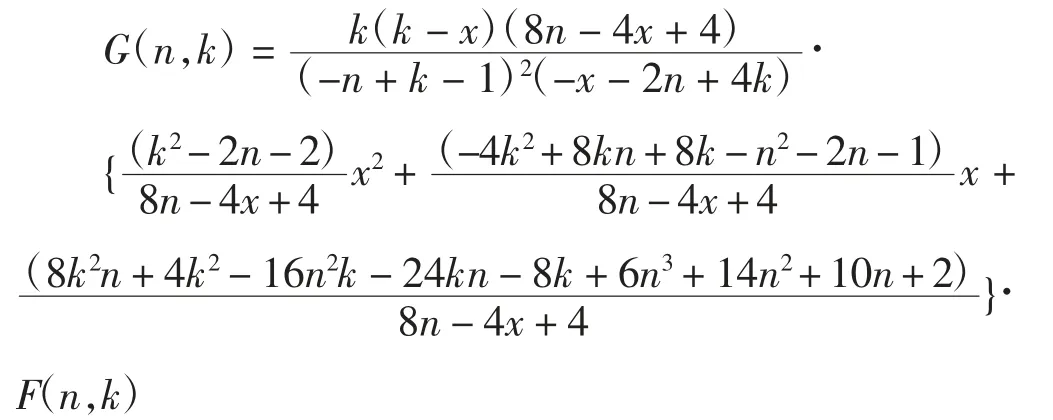
注意到：

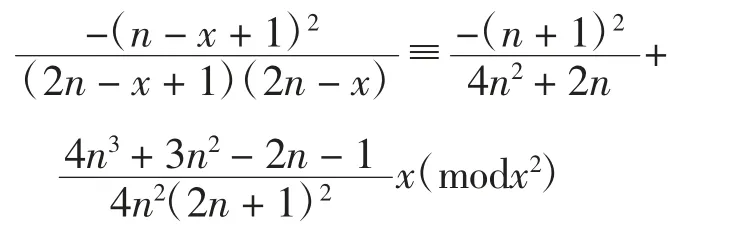
根据式（1），对式（11）取留数并对 k 求和得：

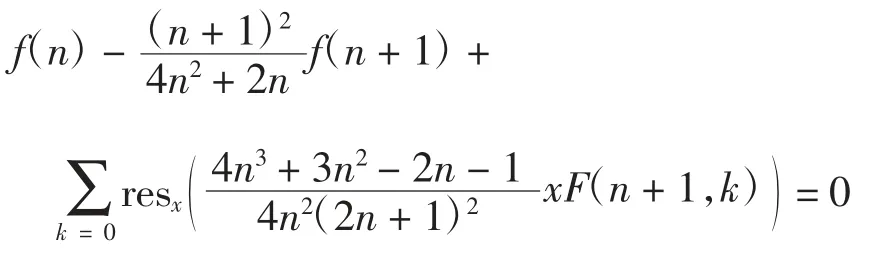
注意到：

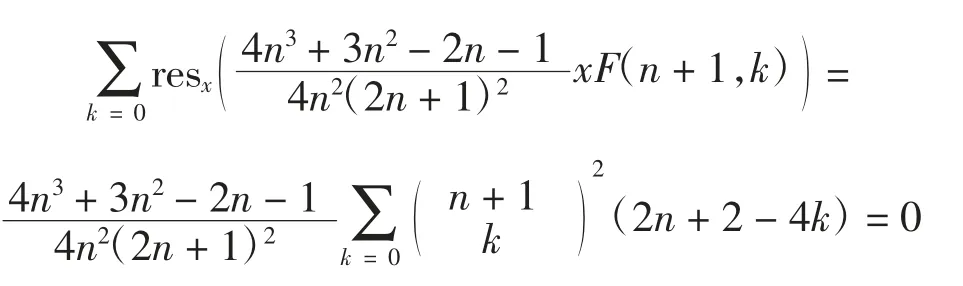
故可得f（n）满足如下递推关系：

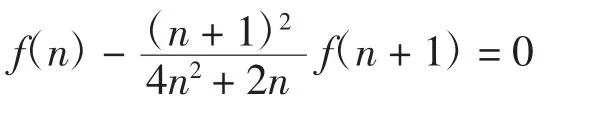
式中：n ＞0，利用f（1）=0 即可证明该恒等式当n ＞0时成立。

注：文献[2]中还考虑了如下和式：

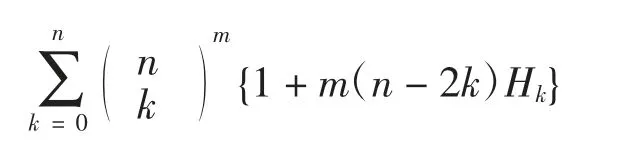
采用本文方法，均可给出相应和式的递推关系式，在此不再赘述。

本文方法也适用于含有一般广义调和数的相应和式。仅以文献[6]中的如下恒等式为例进行说明。

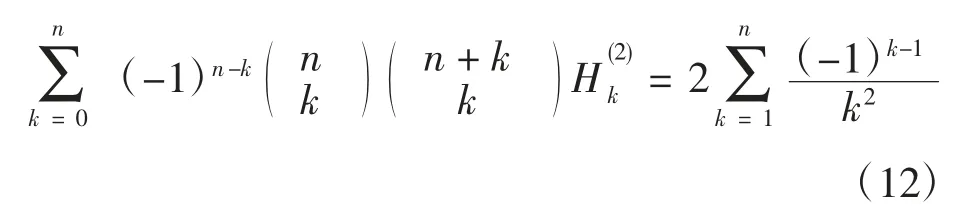
其次，记左端和式为f（n），并记F（n，k）=（-1）n-k·，则由Zeilberger 算法可得：

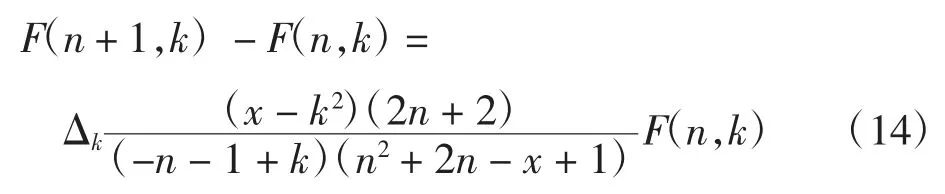
式中：记

同理，利用式（13），对式（14）取留数并对 k 求和，注意到右端为：

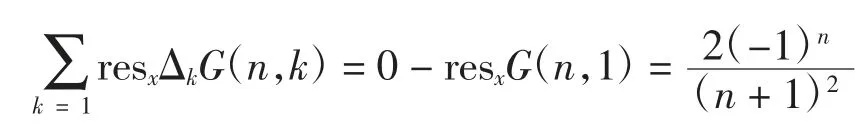
故可得f（n）满足递推关系式：

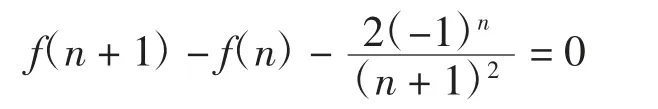
可以验证式（12）右端也满足上述关系且与f（n）有相同初值，故恒等式成立。

3 结 语

本文利用形式留数给出了调和数的一个超几何表示并由此利用经典的机器证明——Gosper 算法和Zeilberger 算法来处理含有调和数的相应和式。通过给出一些经典恒等式的新证明，发现本文方法灵活有效。此外，该方法还可用于证明含有广义调和数的相应恒等式。在后续的研究中，一方面，将进一步扩展该方法并将其用于发现新的恒等式；另一方面，还将研究该方法在证明含有调和数的超同余式中的应用。