钢箱梁顶推参数影响及稳定性分析

谢福君，张家生

钢箱梁顶推参数影响及稳定性分析

谢福君1,2，张家生1

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 衡阳市交通运输局，湖南 衡阳 421001)

为了研究钢箱主梁顶推施工过程的受力特点及其局部稳定性，结合某钢箱自锚式悬索桥，分析导梁的各个设计参数对顶推过程受力及变形的影响，分析表明导梁前端最大位移、导梁根部弯矩及钢箱梁最大拉、压应力均随顶推过程呈现周期性的变化，导梁的弹性模量及泊松比的变化对顶推过程受力及变形的影响较小，导梁的长度及其平均线重度对顶推过程受力及变形的影响较大。其次，以弹性薄板的小挠度理论为基础，分析钢箱梁顶推过程的局部稳定性，计算表明，钢箱梁未加劲前，局部稳定性不满足要求，加劲之后则满足要求。考虑板组间的约束因素、材料非线性、初始几何缺陷及残余应力等的影响，结构自重引起的应力对结构的屈曲临界应力影响很小，可以忽略不计；横隔板的设置对提高钢箱梁局部屈曲效果明显。

钢箱梁；顶推；施工过程；影响分析；局部稳定

大跨径的自锚式悬索桥，一般情况下，考虑到场地的限制和成本控制等因素，主梁施工多采用顶推法。李传习等[1]对中国、日本和英国钢结构局部稳定设计规范有关轴心受压板件局部稳定验算方法进行比较、分析，提出对轴向受压钢箱梁不同板件或者组合板件进行局部稳定验算时推荐采用的相应规范及其条文。刘刚[2]对美国规范和中国规范中钢结构抗震局部稳定进行分析和比较。郭青锋 等[3]对猎德大桥顶推过程中钢箱梁局部稳定进行分析，并根据规范公式对加紧肋进行宽厚比验算。张玉平等[4]运用有限元软件ANSYS，根据施工方案对嘉绍大桥钢箱梁施工过程中的2个最不利工况进行穗定性和强度验算分析。李立峰等[5]以某大跨度自锚式悬索桥为例，进行2个不同结构布置的扁平钢箱梁局部稳定模型试验，得到了模型的变形、应力分布规律以及失稳荷载、破坏形式，提出考虑材料与几何双重非线性、初始几何缺陷和残余应力的极限承载力分析方法。施刚等[6]对4个Q460钢材等边箱形短柱进行轴心受压试验。根据试验结果分析试件的局部屈曲应力、极限应力随板件宽厚比的变化规律，并将试件的局部屈曲应力、极限应力与我国、美国、欧洲钢结构设计规范以及陈绍养建议的相应设计方法和计算公式进行对比分析。已有的关于顶推施工的分析多集中于混凝土主梁[7−13]，对于钢结构的顶推施工过程分析的文献较少[14−15]，尤其是顶推施工过程的局部稳定性的报道几乎没有。为此，本文以某桥为例，进行钢箱梁的顶推施工的参数影响分析及其局部稳定性评价。

1 顶推施工及计算简介

顶推法是指梁体在桥头逐段浇筑或拼装，用千斤顶纵向顶推主梁，使梁体通过各墩顶的临时滑动支座面就位的施工方法。随着主梁节段逐段向前推进，连续梁桥全桥每个截面的内力不断地从负弯矩→正弯矩→负弯矩…，呈周期反复性的变化。顶推法施工恒载内力计算，一般采用有限元方法计算，现以图1受力体系为例，简要介绍其求解步骤与方法。

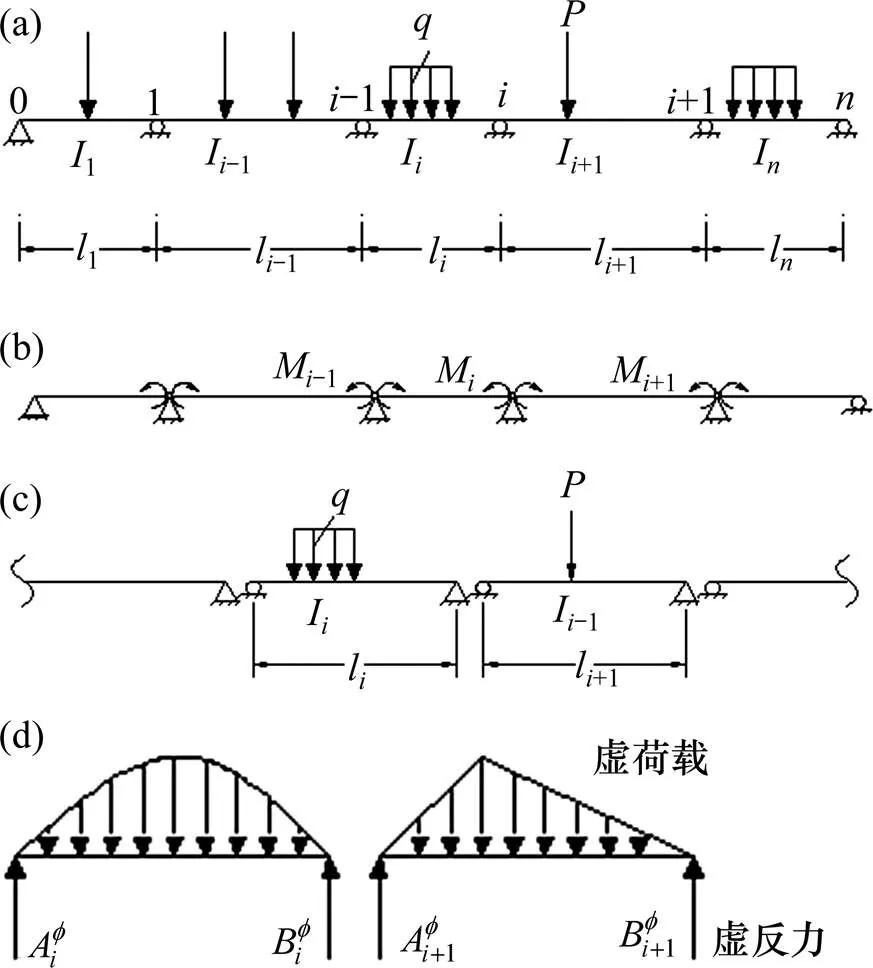
(a) 受力分析模型；(b) 基本结构；(c) 荷载分解；(d) 虚梁反力

2) 按下述通式列出对每个支座(号)的三弯矩方程，即：

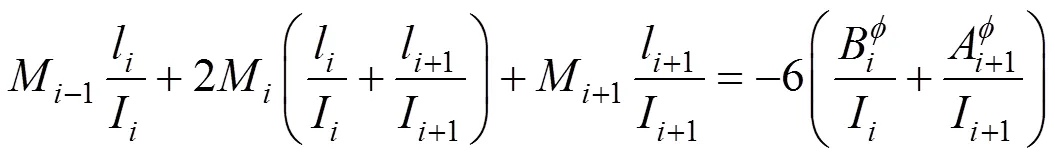
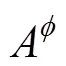
4) 固端及悬臂端的处理

将图1(a)所示结构化为图1(b)的等代结构后，再重复上述1~3步骤，便可得到问题的解。

2 工程简介及MIDAS计算模型

某双塔三跨自锚式悬索桥，主桥跨径布置为：60 m+120 m+60 m。设计荷载：城-A级，公路Ⅰ级，人群荷载按《城市桥梁设计规范》计算取值。该桥钢箱加劲梁采用顶推法施工，主梁顶推就位后，采用PPWS方法架设主缆，并安装吊杆，最终成桥。

为了减小主梁顶推施工难度，在1号~2号跨跨中设置临时墩，钢箱加劲梁顶推导梁采用变刚度导梁，由根部向端部逐渐减小。导梁与主梁连接位置采用大箱型结构，其他位置采用双H型结构，2幅导梁间及双H型结构间采用Φ140×4的钢管做成的桁架作为支撑。为方便导梁过前方顶推墩，导梁端部设计成台阶状，方便起顶。导梁主体结构采用Q345b钢材，联接撑采用Q235b。

该桥主桥加劲梁采用等高钢箱梁(中心梁高2.535 m)，其顶板、底板及腹板的内侧均布置有开口型或闭口型加劲肋，在进行截面特性计算时，可采用换算特性等效的方法进行分析。主梁顶推计算分析采用MIDAS软件进行。采用梁单元计算模型(297个单元，298个节点)，模型的边界条件为结构支座位置的竖向线位移约束和墩底固结。全桥共划分为75个施工阶段进行仿真分析计算。

3 参数影响分析

根据顶推施工过程的特点，分别选择导梁的长度及其平均线重度为参数对顶推施工过程的内力及变形进行参数影响分析。参数分析基准见表1。计算结果见图2~5。

表1 顶推参数影响分析基准

随着钢箱梁的顶推，导梁前端的挠度呈现周期性变化，最大挠度出现在第1跨最大悬臂状态，为1.201 13 m。

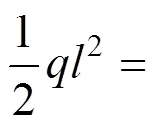
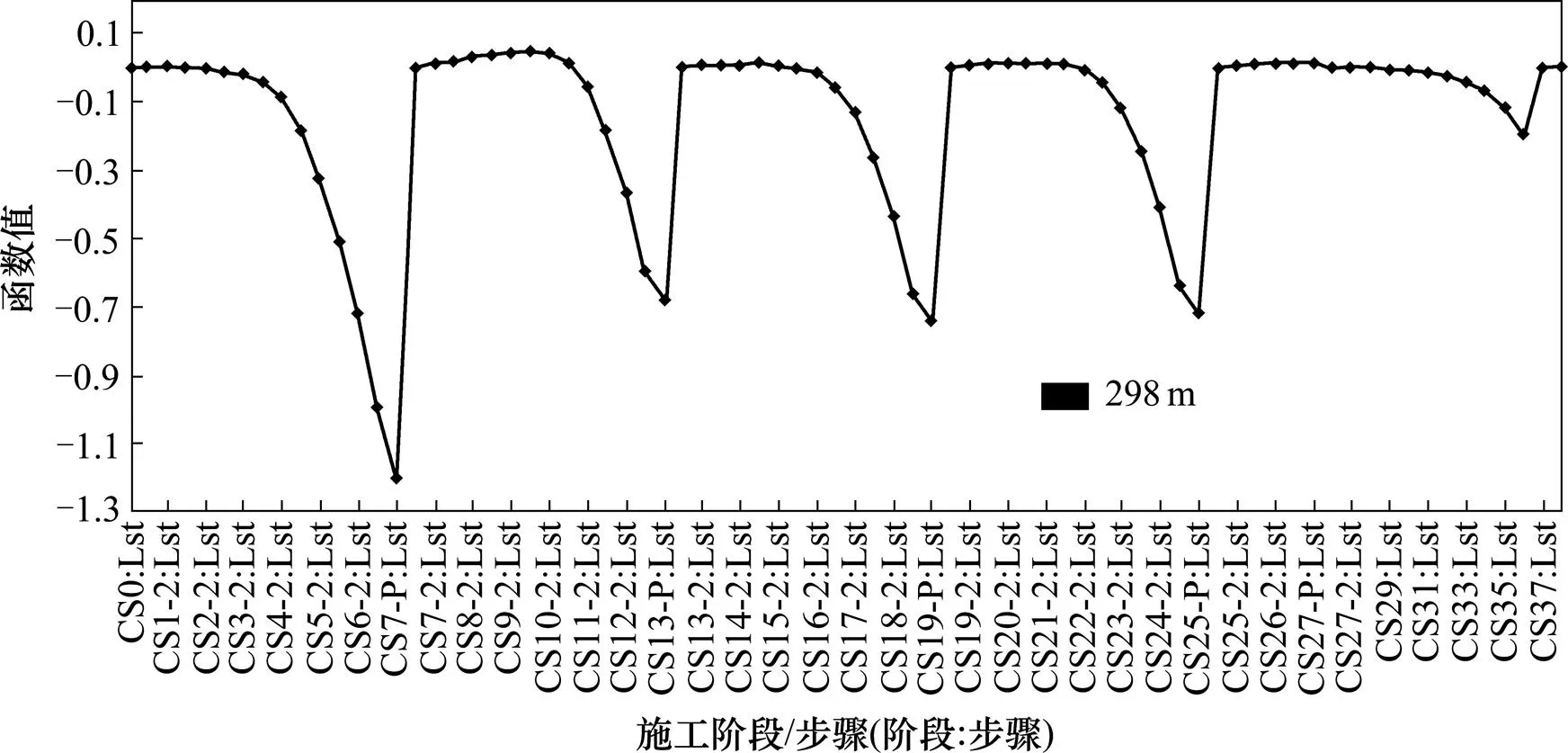
图2 导梁前端位移随施工阶段/步骤

图3 导梁根部弯矩随施工阶段/步骤图

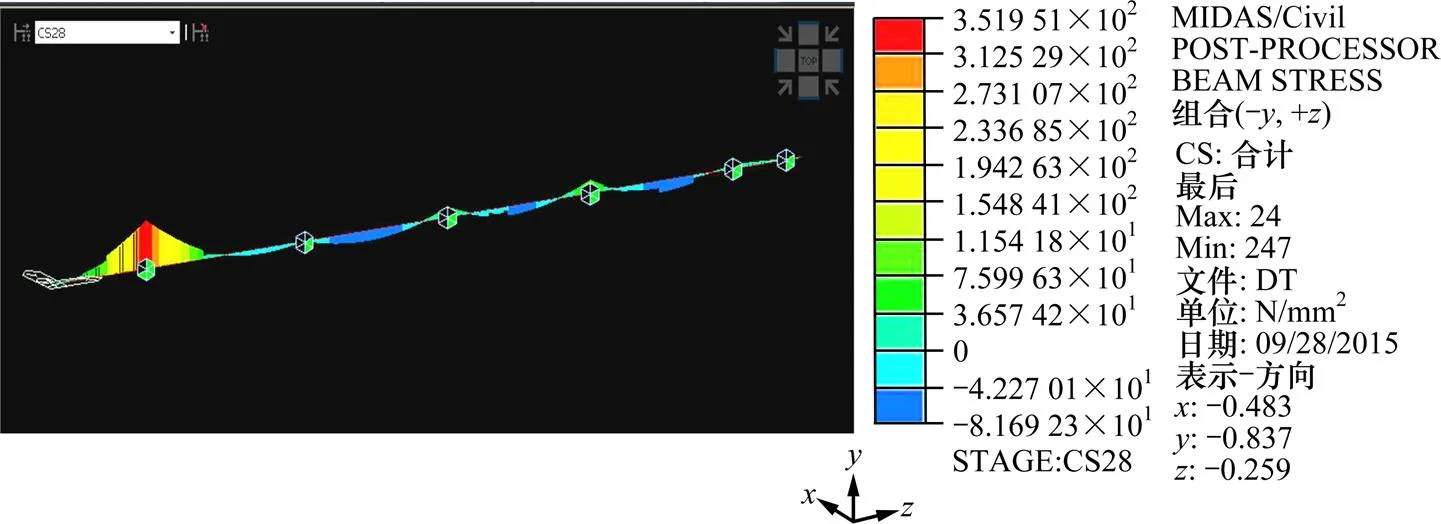
图4 主梁顶推阶段顶部最大拉应力(CS28, Max=351.951 MPa)

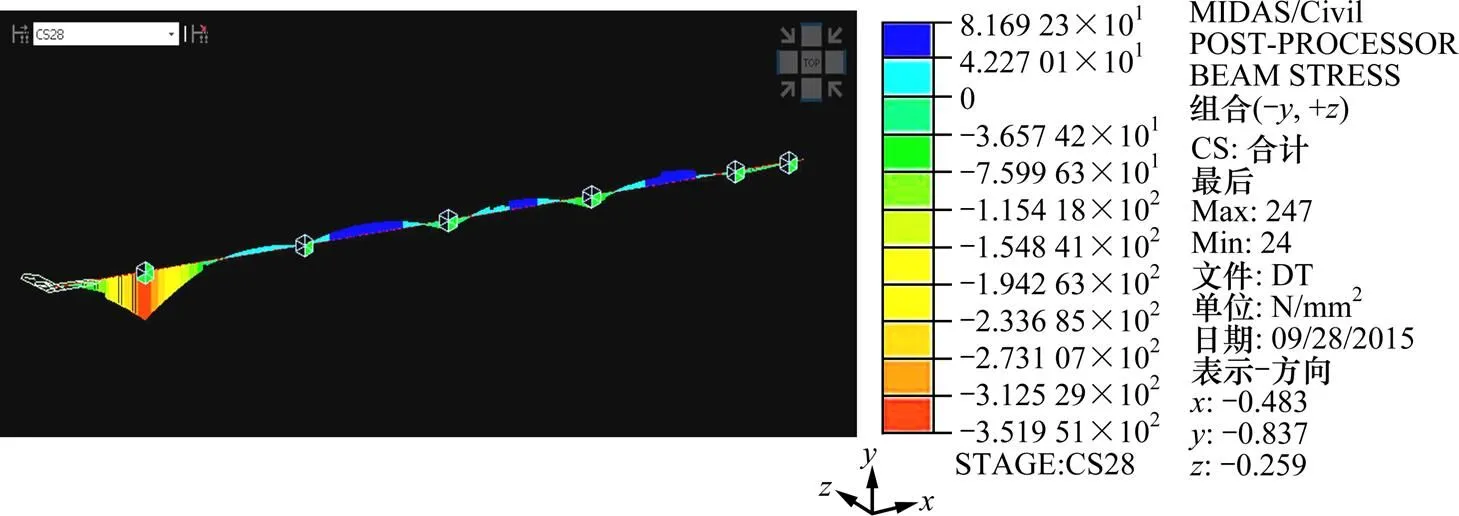
图5 主梁阶段顶部底部最大压应力(CS28, Max=351.951 MPa)

由图4~5可得，钢箱梁顶、底板最大拉、压应力出现在CS28状态，此时最大应力为351.951 MPa，小于容许应力380 MPa，强度满足要求。

3.1 导梁长度影响分析

该桥导梁的设置长度为45 m，顶推阶段的最大跨径60 m，两者之比为0.75。根据《城市桥梁工程施工与质量验收规范》(CJJ2—2008)，导梁长度宜为顶推跨径的0.6~0.8倍，以此为基准，本文分析选取导梁长度及计算分析结果见表2。

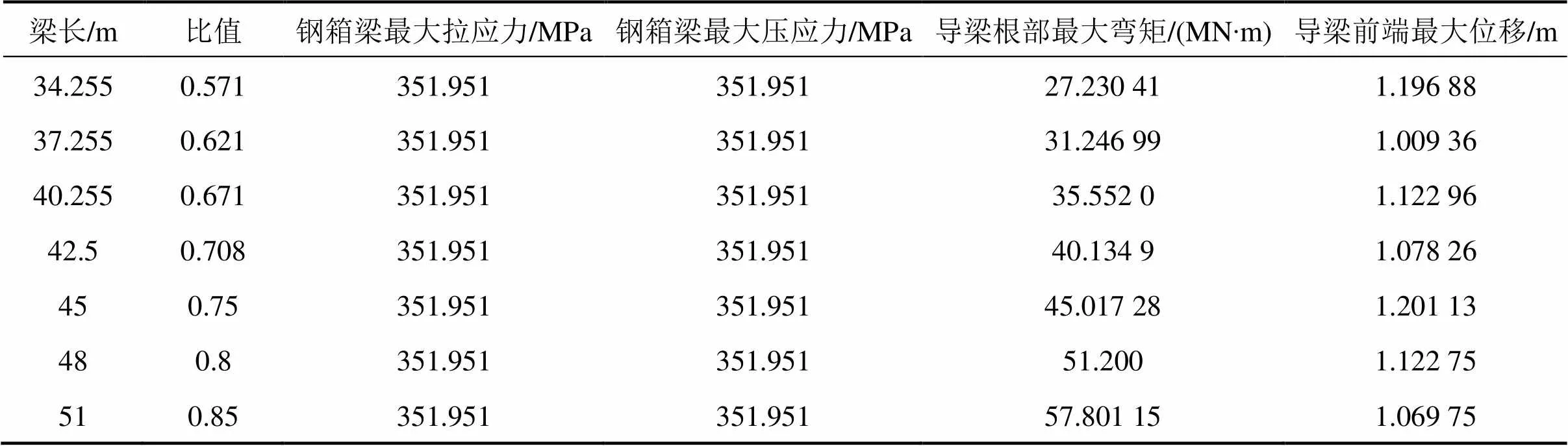
表2 导梁的长度变化分析结果

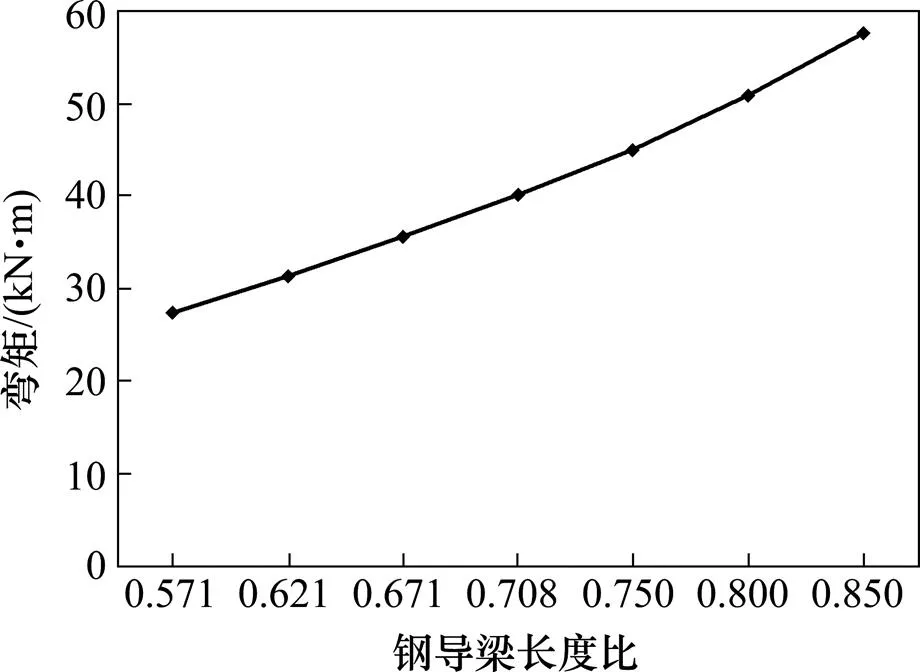
图6 导梁根部弯矩随导梁长度比变化

图7 导梁前端位移随导梁长度比变化

随着导梁的长度变化，导梁前端的位移随着导梁长度的增大呈现周期性变化，产生这种现象的原因是，当导梁的长度小于跨径长度时，其最大位移为一跨的外伸最大悬臂状态，随着导梁长度的增大，位移逐渐增大；当导梁的长度大于跨径长度时，其最大位移为两跨的外伸最大悬臂状态，随着导梁长度的增大，位移逐渐增大。

计算分析表明，钢主梁的最大拉、压应力均出现在连续梁两端双悬臂状态，且不随导梁长度的变化而变化，为恒常数。

3.2 导梁平均线重度影响分析

该桥设计导梁的折算重度为44.44 kN/m，现以长度不变，改变导梁重度0.6~1.1倍，计算分析结果见表3。

表3 导梁的线重度变化分析结果表

由表3、图8~9可得，随着导梁折算重度的增大，导梁根部最大弯矩、导梁前端最大位移随之增大，均呈现线性关系，其线重度变化量与其弯矩变化量及其位移变化量之比分别为0.977 9 kN∙m/ MN∙m和53.492 84 kN∙m/m。分析表明，钢箱梁的最大拉、压应力不随导梁折算重度的变化而变化，为恒常数。

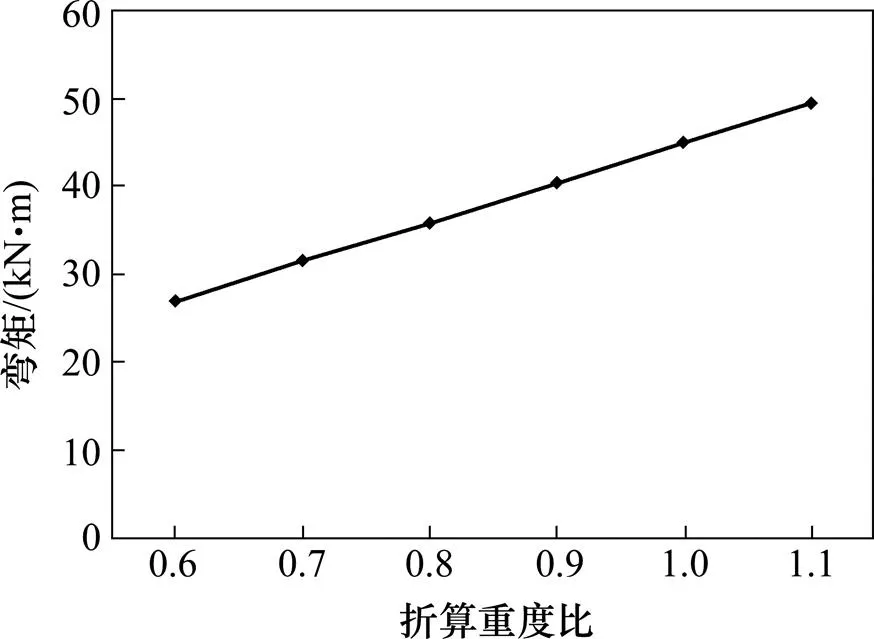
图8 导梁根部弯矩随其平均线重度变化

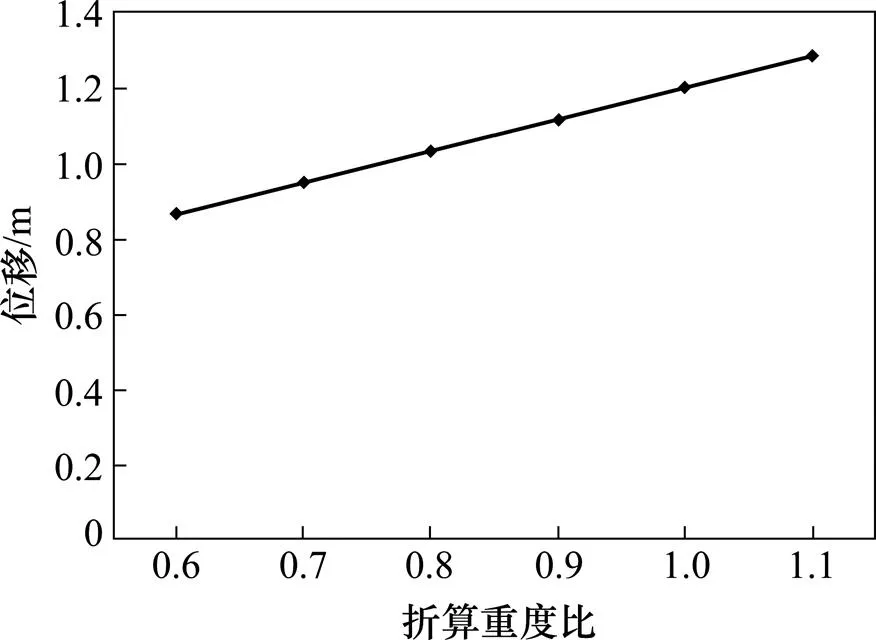
图9 导梁前端位移随其平均线重度变化

4 钢箱梁顶推局部稳定性控制

根据弹性薄板的小挠度理论，任取薄板一微分块平衡，见图10。

分析整理可得，薄板的稳定方程见式(2)。

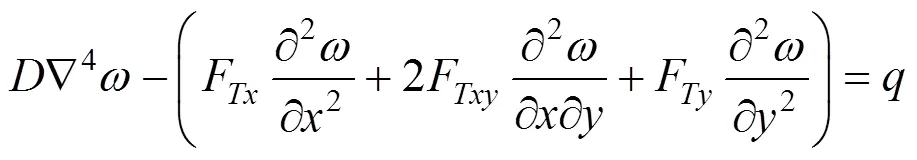
钢箱梁顶推过程中，选取不同位置板块进行分析，横向荷载=0或相比结构内力很小可以忽略。这时根据板端约束条件及受荷情况，采用(重)三角级数求解，可得相应纵向荷载F的临界值，如下 所述：

四边简支，一对边受单位长度均布压力F(作用于长度边)：

只有管理层理解了内部控制的重要意义，才能为单位各部门和全体员工做好表率作用，认真对待行政事业单位的内部控制建设工作，加大建设的投入并且严格遵守内部控制管理制度中的各项规章，逐渐将内部控制意识从管理层渗透到单位员工层面。为了使内部控制的意识深入到员工内部，行政事业单位需要定期举办相关的团建活动和知识讲座，通过培训来强化内部控制在行政事业单位工作中的重要性，并向员工严格明确内部控制制度的权威性。行政事业单位应该通过管理层指导各部门、各部门监督员工落实的方式不断完善内部控制体系，同时强化全体员工的工作思维模式。

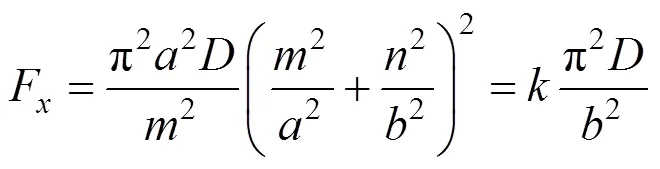
四边简支，一对边受单位长度均布压力F(作用于长度边)，另一对边受均布压力F=αF(作用于长度边)：

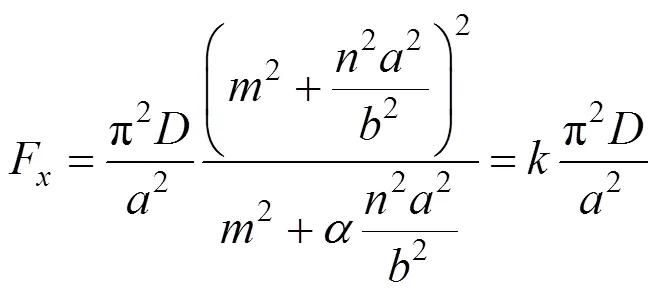
式中：k为板的稳定系数。，n=1，m=1，k取极小值。Fy为拉力时，α为负。

三边简支，与压力平行一边自由，一对简支边受单位长度均布压力F(作用于长度边)：

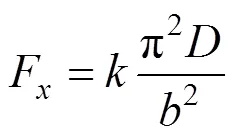
式中：为板的稳定系数，表达式为求解四阶系数行列式等于0的解，限于篇幅，具体表达式略。分析结果，当时，取极小值0.425，其余情况下，值与泊松比及/的值有关。

一对边固定，另一对边简支且受单位长度均布压力F(作用于长度边)。临界荷载F的表达式见式(5)。分析表明：当0.7时取极小值6.97，其余情况下，值与的值有关。

一对边固定，另一对边一边固定，另一边简支且受单位长度均布压力F(作用于长度边)。临界荷载F的表达式见式(5)。分析表明取极小值5.42，其余情况下，值与/的值有关。

一对边固定，另一对边一边固定，另一边自由且受单位长度均布压力F(作用于长度边)。临界荷载F的表达式见式(5)。分析表明取极小值1.28，其余情况下，值与泊松比及/的值有关。屈曲临界应力：

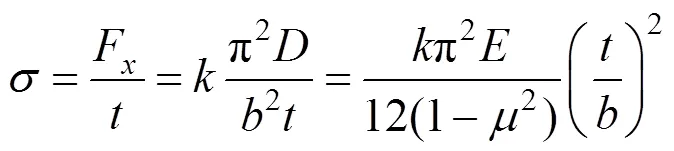
钢箱梁顶推各个施工阶段，主梁均为压弯构件，承受弯压应力。计算分析表明，顶推阶段最大压应力为351.951 MPa。选取主梁典型断面见图11，标准节段长度5 m，内设2块横隔板，最大间距 1.67 m。

选取顶板(5 m×2.8 m×22 mm)进行分析，不考虑顶推千斤顶作用附近钢板的局部应力变化，根据圣维南原理，按式(5)计算，F=14.70 MPa<< 351.951 MPa，说明其在顶推压力作用下会发生屈曲，产生局部失稳，需要采取加劲措施；采用图12所示加劲设计，任意选取一段纵向加紧肋间顶板(5 m×0.35 m×22 mm)为例进行分析，按式(5)计算，F=940.64 MPa>>351.951 MPa，表明结构局部失稳满足要求。

同理选取底板(5 m×2.8 m×24 mm)进行分析，按式(5)计算，F=17.49 MPa<<351.951 MPa，说明其在顶推压力作用下会发生屈曲，产生局部失稳，需要采取加劲措施；采用图12所示加劲设计，任意选取一段纵向加紧肋间底板(5 m×0.35 m×24 mm)为例进行分析，按式(5)计算，F=1119.4 MPa>>351.951 MPa，表明结构局部失稳满足要求。

同理选取腹板(5 m×2.5 m×16 mm)进行分析，按式(5)计算，F=9.75 MPa<<351.951 MPa，说明其在顶推压力作用下会发生屈曲，产生局部失稳，需要采取加劲措施；采用图12所示加劲设计，选取一段纵向加紧肋间腹板(5 m×0.415 m×16 mm)为例进行分析，按式(5)计算，F=353.88 MPa> 351.951 MPa，表明结构局部失稳满足要求。但是安全储备偏小，应需严格控制施工过程，确保安全。

实际计算板件局部稳定时，还应考虑板组间的约束因素、材料非线性、初始几何缺陷及残余应力等的影响，计算所得屈曲应力小于式(5)的计算结果。考虑上述因素通常采用有限元软件进行分析，分析模型及分析结果分别见图12，表4。

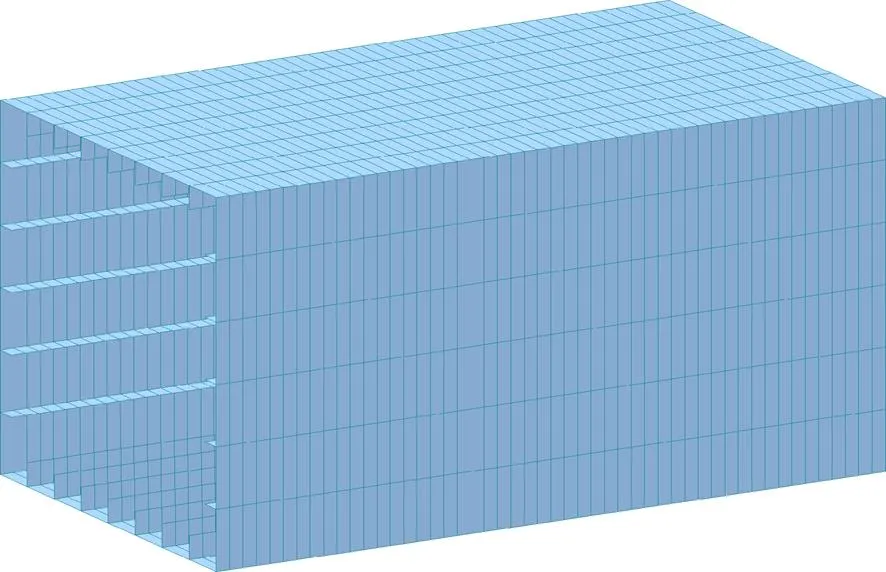
图12 钢箱梁局部稳定计算模型

表4 钢箱梁局部屈曲分析结果表

注：1) 表示不考虑横隔板及结构自重的影响；2) 表示考虑结构自重但不考虑横隔板的影响；3) 同时考虑结构自重及横隔板的影响。

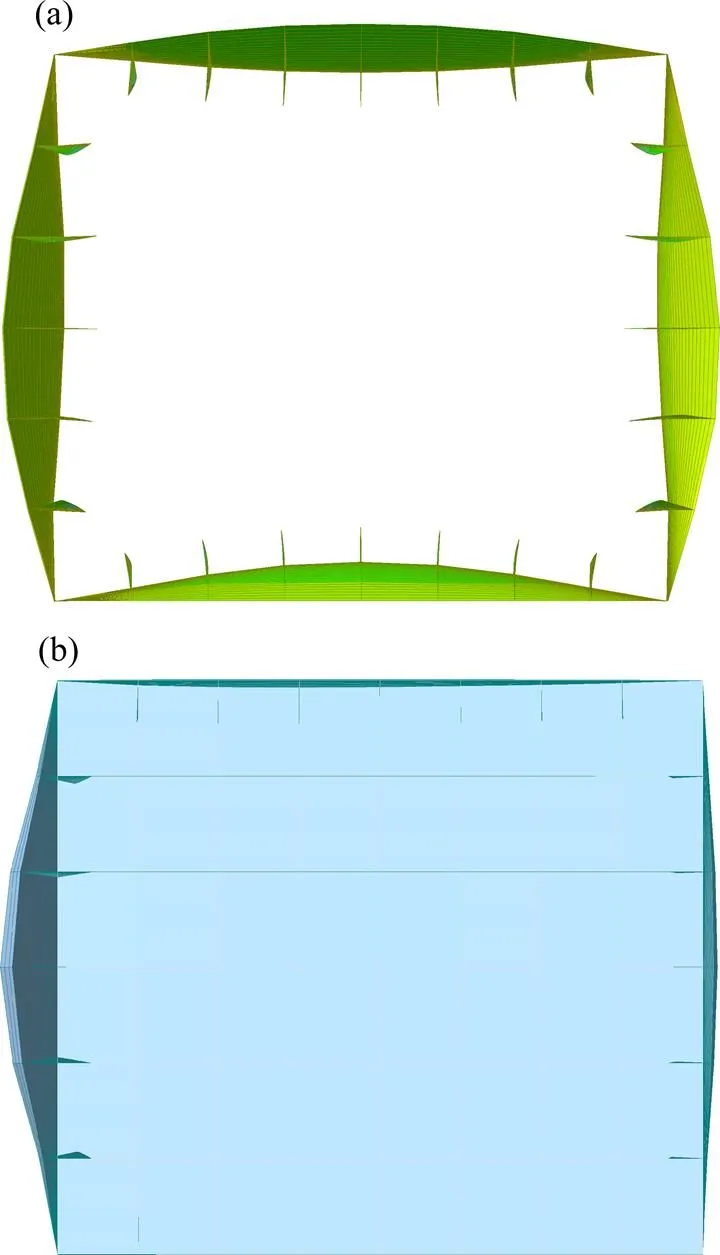
(a) 不考虑横隔板的影响；(b) 考虑横隔板的影响

计算分析表明，不考虑横隔板的影响，在轴向压力作用下，箱形截面四周板件同时屈曲，屈曲模态见图13(a)。考虑横隔板的影响，腹板首先发生局部屈曲，屈曲模态见图13(b)。

由表4可得，不考虑横隔板及结构自重的影响，轴向压力临界值为13 232.13 kN；不考虑横隔板、考虑结构自重，轴向压力临界值为13 306.65 kN，略小于不考虑结构自重的临界压力值，为其0.994 4倍，表明结构自重本身引起的弯曲应力对结构的屈曲临界应力影响很小，可以忽略不计；同时考虑横隔板及结构自重，轴向压力临界值为42 421.60 kN，为不考虑横隔板考虑结构自重的临界轴力值的3.188倍，表明横隔板的设置对提高钢箱梁局部屈曲效果明显。同时不难看出，钢箱梁局部屈曲应力小于结构工作的最大应力，再次说明顶推过程存在失稳的风险。

5 结论

1) 结合某钢箱自锚式悬索桥桥，分析导梁的各个设计参数对顶推过程受力及变形的影响。

2) 导梁前端最大位移、导梁根部弯矩及钢箱梁最大拉、压应力均随顶推过程呈周期性的变化。

3) 导梁的长度及其平均线重度对顶推过程受力及变形的影响较大。导梁根部的最大弯矩随着导梁长度的增大而增大，呈线性关系，其长度变化量与其弯矩变化量之比为0.547 75 m/MN∙m；导梁前端的位移随着导梁长度的增大呈周期性变化。

4) 随着导梁折算重度的增大，导梁根部最大弯矩、导梁前端最大位移随之增大，均呈线性关系，其线重度变化量与其弯矩变化量及其位移变化量之比分别为0.977 9 kN∙m/MN∙m，53.49284 kN∙m/m。

5) 钢箱梁的最大拉、压应力不随弹性模量、泊松比、导梁长度及其折算重度的变化而变化，为恒常数。

6) 采用理论公式计算表明，钢箱梁未加劲前，局部稳定性不满足要求，采用加劲之后，局部稳定性基本满足要求，但是安全储备很小，需要严格控制顶推施工过程。

7) 采用有限元模型分析表明，结构自重本身引起的弯曲应力对结构的屈曲临界应力影响很小，可以忽略不计；横隔板的设置对提高钢箱梁局部屈曲效果明显。

[1] 李传习, 邹桂生. 轴心受压钢箱梁局部稳定验算方法综述[J]. 中外公路, 2006, 26(3): 129−133. LI Chuanxi, ZOU Guisheng. Local stability calculation methods review for axial compression steel box girder[J]. Journal of China & Foreign Highway, 2006, 26(3): 129− 133.

[2] 刘刚. 中国和美国钢结构抗震局部稳定规定比较[J]. 钢结构, 2011, 26(114): 42−45. LIU Gang. Local stability comparison of seismic provisions between Chinese and American standard[J]. Steel Construction, 2011, 26(114): 42−45.

[3] 郭青锋, 魏民, 奇亮, 等. 猎德大桥钢箱梁顶推过程中局部稳定分析[J]. 四川建筑, 2009, 29(4): 202−203. GUO Qingfeng, WEI Min, QI Liang, et al. Local stability analysis of steel box girder of Liede bridge in incremental launching process[J]. Sichuan Architecture, 2009, 29(4): 202−203.

[4] 张玉平, 袁鹏, 罗超云, 等. 嘉绍大桥钢箱梁施工过程中局部稳定及强度分析[J]. 公路交通科技, 2014, 31(2): 47−53. ZHANG Yuping, YUAN Peng, LUO Chaoyun, et al. Analysis on local stability and strength of steel box girder in construction process of Jiaxing Shaoxing Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 47−53.

[5] 李立峰, 邵旭东, 易伟建, 等. 扁平钢箱梁局部稳定模型试验[J]. 中国公路学报, 2007, 20(3): 60−65. LI Lifeng, SHAO Xudong, YI Weijian, et al. Model test on local stability of flat steel box girder[J]. China Journal of Highway and Transport, 2007, 20(3): 60−65.

[6] 施刚, 林错错, 王元清, 等. 高强度钢材箱形截面轴心受压短柱局部稳定试验研究[J]. 工业建筑, 2012, 42(1): 18−25. SHI Gang, LIN Cuocuo, WANG Yuanqing, et al. Experimental study on local buckling of high square box section stub columns under axial strength steel compression[J]. Industrial Construction, 2012, 42(1): 18−25.

[7] 田仲初, 陈耀章, 赵利平, 等.连续钢梁顶推过程局部接触分析及改善措施[J]. 长安大学学报(自然科学版), 2012, 32(4): 44−50. TIAN Zhongchu, CHEN Yaozhang, ZHAO Liping, et al. Local contact analysis and improvement measures of continuous steel girder incremental launching[J]. Journal of Chang’an University (Natural Science Edition), 2012, 32(4): 44−50.

[8] 董创文, 李传习, 张玉平, 等. 变曲率竖曲线梁顶推过程支点标高调整方案确定的单步模数搜索合成法[J].土木工程学报, 2015, 48(1): 101−111. DONG Chuanwen, LI Chuanxi, ZHANG Yuping, et al. Single-step modulus search and composition method for determining the scheme of support elevation adjustment during girder launching with vertically varied curvatures [J]. China Civil Engineering Journal, 2015, 48(1): 101− 111.

[9] 秦林, 陈进芬, 胡海洋, 等. 北盘江大桥合龙顶推方案研究[J]. 世界桥梁, 2013, 41(3): 43−46. QIN Lin, CHEN Jinfen, HU Haiyang, et al. Study of incremental launching schemes for closure of Beipanjiang River bridge[J]. World Bridges, 2013, 41(3): 43−46.

[10] 陈双庆, 谭光耀. 单点顶推施工支撑墩受力分析及优化研究[J]. 湖南交通科技, 2015, 41(3): 92−95. CHEN Shuangqing, TAN Guangyao. Supporting pier stress analysis and optimization research with direct incremental launching[J]. Hunan Communication Science and Technology, 2015, 41(3): 92−95.

[11] WANG J, LIN J, CHEN C, et al. Simulation analysis and control research of long multi-span composite bridge with incremental launching construction[C]// Proceedings of the 11th International Conference of Chinese Transportation Professionals. Nanjing, 2011: 3078−3090

[12] 张晓东. 桥梁顶推施工技术[J]. 公路, 2003(9): 45−51. ZHANG Xiaodong. The incremental launching technology of bridge[J]. Highway, 2003(9): 45−51.

[13] Beaney N J, Martin J M. Design and construction of the Dornoch Firth Bridge[C]// Proceedings of Institution Civil Engineerings, Transportation, Beijing, 1993: 145− 156.

[14] Rosignoli Macro. Prestressing schemes for incrementally launched bridges[J]. Journal of Bridge Engineering, 1999(5): 107−115.

[15] 董创文, 李传习, 王琛．考虑相位变化及组拼高程误差的顶推梁体无应力线形的实现[J].土木工程学报, 2013, 46(8): 74−82. DONG Chuangwen, LI Chuanxi, WANG Chen. Achieving unstressed geometry of incrementally launched girders considering phase shift and elevation deviation during assembly stage[J]. China Civil Engineering Journal, 2013, 46(8): 74−82.

Influence analysis and stability analysis for incremental launching of steel box girder

XIE Fujun1,2, ZHANG Jiasheng1

(1.Shool of Civil Engineering, Central South University, Changsha 410075, China; 2. Transport Bureau of Hengyang City, Hengyang 421001, China)

In order to further study stress characteristics and the local stability of steel box girder during incremental launching construction, first, combined with a self-anchored suspension bridge with steel box girder, influence analysis for incremental launching process with design parameters was carried out. Analysis shows that maximal displacement at the front of guide beam, bending moment at steel guide beam root and maximum tensile stress of steel box girder as well as compressive stress of steel box girder are periodicalchange along with the construction process. Meanwhile, elastic modulus and Poisson ratio have a little influence on stress and deformation of steel box girder during incremental launching process, length of steel guide beam and its average weight have an important influence on stress and deformation of steel box girder during incremental launching process. Secondly, on the basis of elastic thin plate theory of small deflection, local stability analysis of steel box girders during the process of incremental launching have been carried out. Theoretical calculation shows that local stability of steel box girder does not meet the requirements before stiffening, after stiffening, the requirements is meet. Considered constraint factors between plate groups, material nonlinearity and initial geometric imperfection and residual stress, finite element analysis showed that the stress by self weight has a little influence on critical buckling stress, it can be neglected; Installing diaphragm plate to improve the effect of local buckling of steel box girder is obvious.

steel box girder; incremental launching; construction process; influence analysis; local stability

U445.462；U441+.5

A

1672 − 7029(2019)06− 1484 − 09

10.19713/j.cnki.43−1423/u.2019.06.018

2018−07−28

国家自然科学基金资助项目(51378514)

张家生(1964−)，男，湖南长沙人，教授，博士，从事土木工程设计与施工仿真研究；E−mail：zjsdj@mail.csu.edu.cn

(编辑 阳丽霞)