基于极大值原理的地铁列车节能驾驶简化算法

曲健伟，王青元，孙鹏飞

基于极大值原理的地铁列车节能驾驶简化算法

曲健伟，王青元，孙鹏飞

(西南交通大学 电气工程学院，四川 成都 611756)

通过在地铁列车定时节能驾驶优化问题中引入目标牵引恒速高于线路限速的假设，对以往基于极大值原理分析得到的节能驾驶工况集和节能工况使用时机进行简化，将给定目标牵引恒速下的节能速度曲线求解问题简化为在最大能力运行牵引和制动工况基础上寻求最优惰行连接段的问题。根据最大能力运行的工况结果对线路进行区段划分，并引入连接函数和连接误差对惰行工况的连接效果进行表征，基于最优工况切换条件，提出给定目标牵引恒速条件下求解最优惰行连接段的数值算法，并构造给定区间运行时间要求下的最优节能速度曲线计算算法。采用哈尔滨地铁3号线的列车和线路数据对算法进行验证，计算结果证明了假设的合理性，与目前该列车采用的实际驾驶策略相比，本文算法可节能21.92%。

地铁列车；节能驾驶；极大值原理；工况切换条件；连接函数

目前，列车节能驾驶和时刻表节能优化已成为地铁列车节能运行研究的热点[1]。节能驾驶优化是进行列车运行时刻表优化的基础，国内外学者针对该问题进行了大量研究，其中基于极大值原理的方法能够得到理论上的最优解[2−3]。基于极大值原理的节能驾驶研究最早开始于20世纪60年代，Ichikawa[4]将列车节能驾驶优化问题表达为状态变量受约束的最优控制问题，基于平直道假设分析得到节能驾驶工况集以及工况切换时机；Khmelnitsky[5]考虑起伏坡道、变化限速和再生能量利用的可能性，给出了节能驾驶工况集并证明了对于给定的区间运行时间条件下最优策略的存在性和唯一性；LIU等[6]结合线路条件分析得到节能工况的使用时机；Howlett等[7-10]给出了平缓坡道情况下的节能驾驶工况序列，证明陡坡条件下最优工况切换点的唯一性，给出了满足最优工况切换条件的积分公式，证明全局最优切换策略可通过采用局部能耗函数计算每个陡坡区段的最优切换点得到；王青元等[11−12]针对高速列车的节能驾驶，将混合制动的电制动与空气制动分开建模，对节能驾驶工况集和最优工况切换规则进行了分析。以往基于极大值原理的研究侧重于对节能驾驶工况集、节能工况应用条件、最优工况切换条件及最优切换的唯一性进行理论分析，最优工况切换点的计算需要求解包含共轭函数的微分方程组[5, 9−10, 13]，在考虑详细的列车模型和复杂线路条件时计算过程十分复杂，给该方法的工程应用带来了困难。针对地铁列车节能驾驶优化的研究可分为全局速度离散化优化方法[14−15]、基于优秀司机经验的方法[16]和基于节能工况集的方法。石红国等[17−20]学者根据实际线路条件确定节能工况序列，采用不同的搜索算法优化工况切换点位置；柏赟等[21]针对地铁列车在长大下坡上的节能运行，在传统四阶段法的基础上优化节能工况出现的序列和工况转换点。刘炜等[22]根据线路限速和坡道划分子区间，采用时间逼近搜索方法，在最大能力运行速度曲线的高限速到低限速的子区间过渡区段加入惰行来达到节能效果；SU等[23]设定子区间内的最优工况包括最大牵引、惰行、最大制动、恒速牵引、恒速制动，提出一种利用能耗求解节能驾驶策略的方法；GU等[24]分析了子区间在不同坡道和限速情况下的节能驾驶工况序列，并构造了基于非线性规划的操纵模型。基于节能工况集的地铁列车节能驾驶研究仅采用了极大值原理分析得到的节能驾驶工况集和工况序列，并没有使用最优工况切换条件进行工况切换点计算，无法保证求解结果在理论上的最优性。为获得理论上最优的节能驾驶速度曲线，采用基于极大值原理的常规方法[5, 9−10]对地铁列车运行速度曲线进行求解，发现节能工况计算结果中目标牵引恒速工况的速度(即2.1节中的v)总是大于线路限速从而无法实现，其工况切换情况更为简单。基于地铁列车节能运行工况的这一特点，本文引入目标牵引恒速高于线路限速的假设，基于极大值原理的理论分析结果对节能优化方法进行简化，在保证节能驾驶求解最优性的同时，构造适合工程应用的数值算法。

1 节能驾驶优化模型

根据地铁列车运行特点，以列车区间运行采用的牵引加速度和制动减速度为控制变量，考虑列车牵引、制动效率系数和再生能量利用系数，建立以列车区间运行总能耗最小为目标的节能驾驶优化模型。令为列车位置，为速度，为时间，trac，brak，basic和line分别为牵引加速度、制动减速度、基本阻力减速度和线路附加阻力减速度，列车运行状态方程可表示如下[9]：

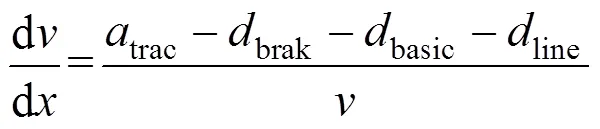
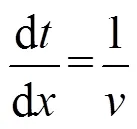
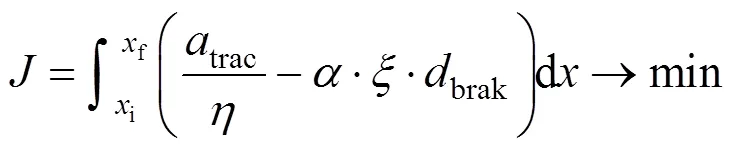
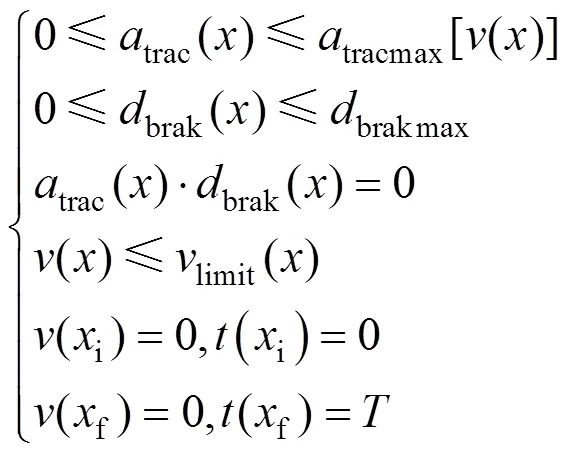
2 节能驾驶优化分析

2.1 节能驾驶工况集及简化

根据极大值原理[5, 9]，引入伴随向量[1,2]，根据式(1)~(3)，哈密顿函数可定义为：

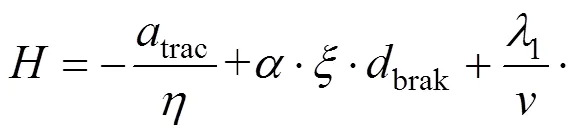
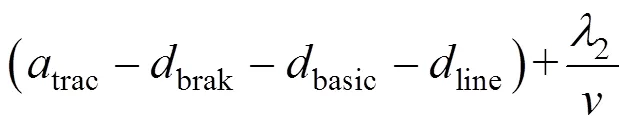
引入处理限速约束的拉格朗日算子，最优控制满足以下方程组：

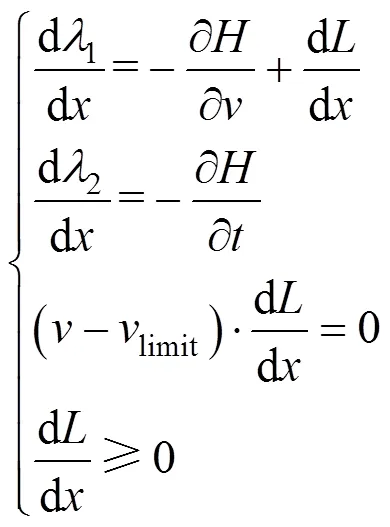
则哈密顿函数变为：

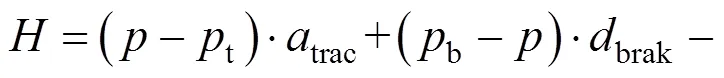
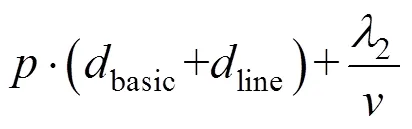
伴随变量的微分方程为：

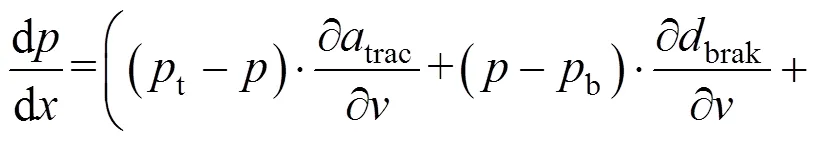
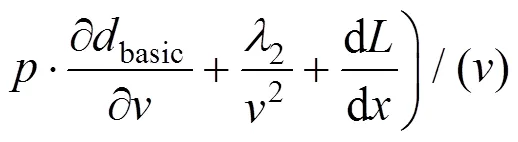
由极大值原理可知，为使取极小值，哈密顿函数需取极大值。节能工况分析如下[9]：

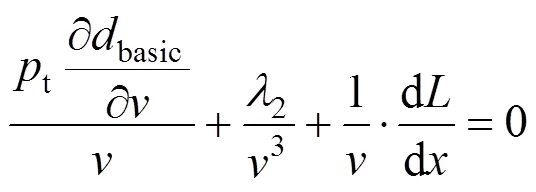
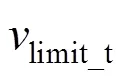
2.2 节能工况使用时机及最优切换条件

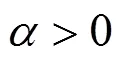
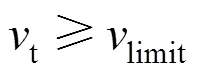
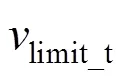
作为连接牵引区段和制动区段的连接工况，惰行工况的伴随变量应满足的最优切换条件为：从牵引区段切入惰行时有=t，从惰行切入制动区段时有=b[5, 9−10]。

3 数值算法

3.1 区段划分

按列车最大能力运行的牵引区段或制动区段，对最大能力运行工况进行区段划分，如图1所示，可知最大能力运行总是由一系列牵引−制动区段对组成。对各区段进行编号，牵引区段编号为奇数，制动区段编号为偶数。

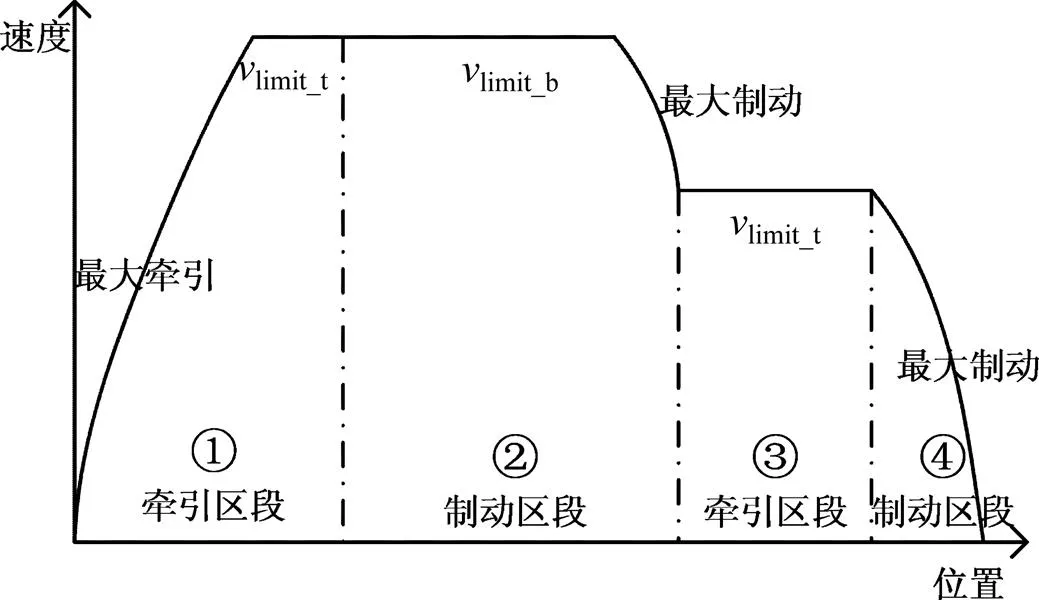
图1 区段划分示意图

3.2 牵引−制动区段对的惰行连接

3.2.1 连接函数定义

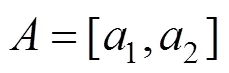
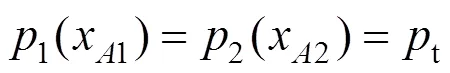
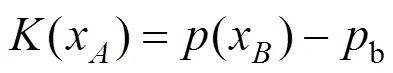
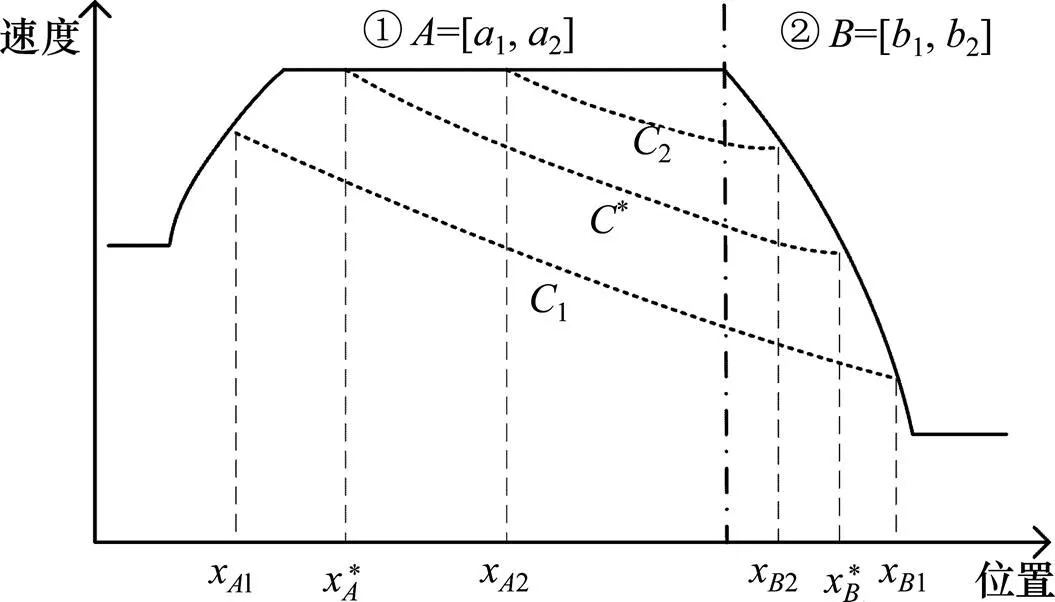
图2 区段连接示意图

3.2.2 连接函数计算

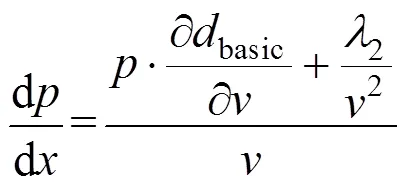
为便于数值计算，将速度和伴随变量的微分方程进行离散化处理，设为位置计算索引，Δ为距离计算步长，令为列车加速度，则有

的计算公式为

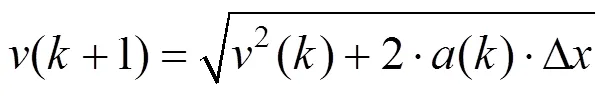
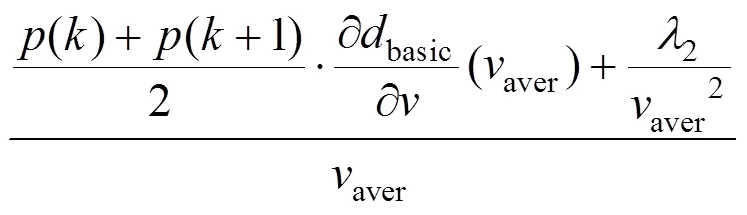
求解得：

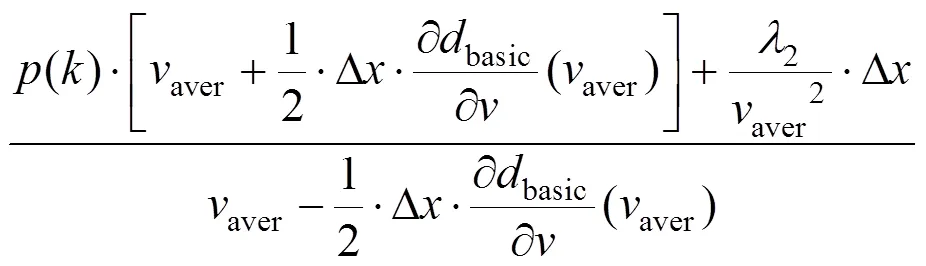
3.2.3 连接误差计算

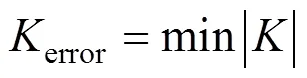
通过计算连接误差，可以得到牵引−制动区段对的最优惰行连接，连接误差的计算算法如下：

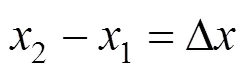
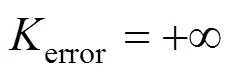
3.3 全程区段连接

根据3.1节的区段划分，设区段个数为，则区段①，③…(−1)为牵引区段，区段②，④…()为制动区段，每个牵引区段可以与其右侧的所有制动区段进行连接误差计算，计算结果如表1所示。

表1 连接误差计算表

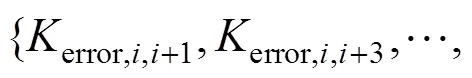
3.4 定时节能算法

列车定时节能优化的算法流程如下。

Step 1：读取区间线路参数、列车参数及特性、运行时间，计算最大能力速度曲线、最大能力控制加速度曲线，t和b；

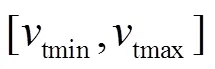
Step 4：针对设定的t和2，根据3.2节的方法计算所有可能的区段连接，并根据3.3节的方法合并连接结果，计算区间运行时间cal；

4 算例分析

4.1 算例1

采用哈尔滨地铁3号线列车及线路数据进行计算，距离计算步长为1 m。列车车长为120 m，AW2载荷下的动态质量为306.12 t，惯性质量为16.9 t，牵引效率系数为0.871，制动效率系数为0.938，再生能量利用系数为0.9。AW2载荷下的基本阻力公式为4.97+0.001 126+ 0.000 0663 62(kN，对应速度单位为m/s)，牵引特性如图3所示，制动减速度最大值为1.12 m/s2。

计算用线路区间长1 565 m，区间坡道、曲线和限速数据分别如表2~4所示。

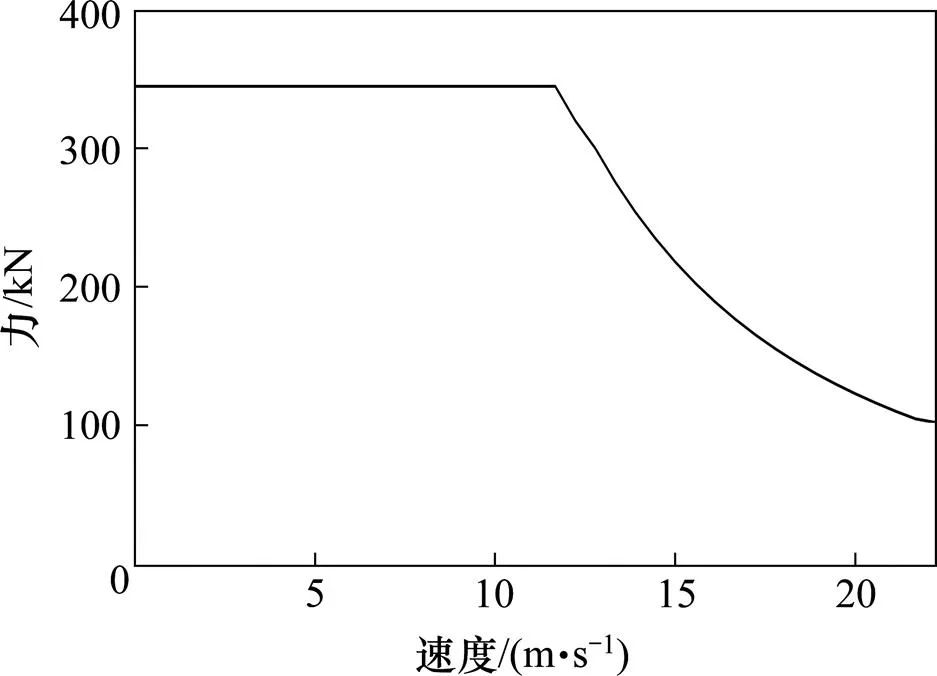
图3 列车牵引特性曲线

根据列车和线路数据进行最大能力计算，最小运行时间为106.48 s，区段划分结果如表5所示，共10个区段。

令t=limit=19.44 m/s计算对应的节能速度曲线，得到的有效连接误差如表6所示，最终确定的牵引−制动区段连接对为①→⑩，对应的区间运行时间为178.98 s。需要注意的是，⑦→⑧也是有效的牵引−制动区段对，但它对应的惰行连接段实际上被①→⑩的惰行连接段所覆盖，故最终的有效牵引-制动区段对只有①→⑩。

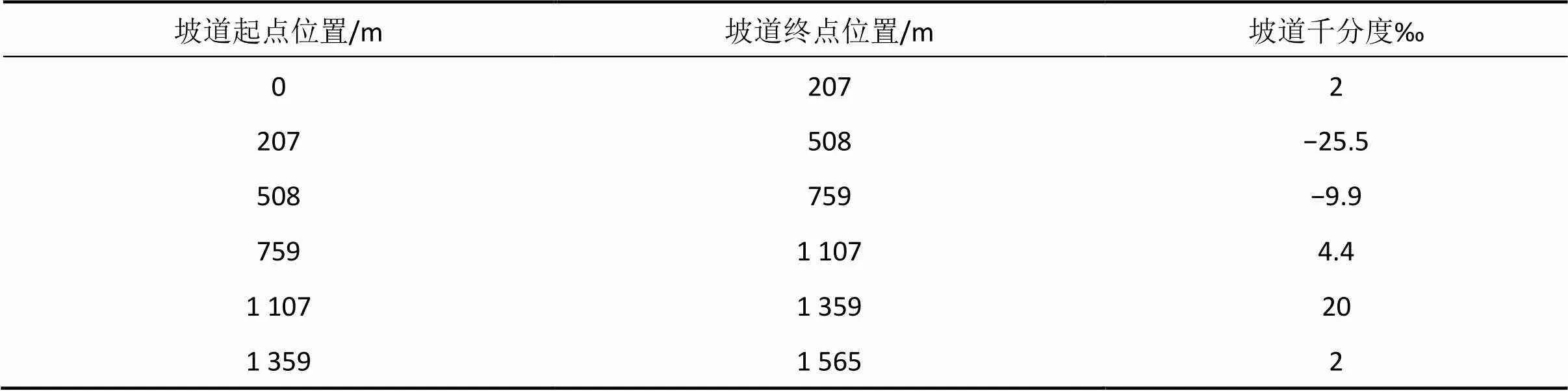
表2 区间坡道数据

表3 区间曲线数据

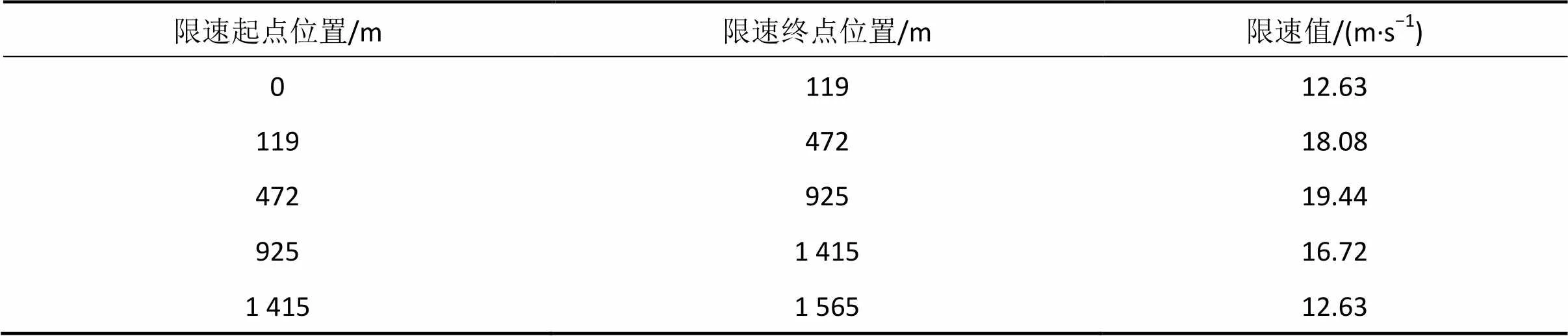
表4 区间限速数据

t变化对应区间运行时间的变化情况如表7所示，t为19.44，60和120 m/s对应的节能速度曲线及最大能力速度曲线如图4所示。由表7和图4可知，随着t的增大，t因高于限速而无法实现，但t取值影响最优惰行段的计算使惰行连接段不断缩短，由一个大的惰行连接段逐渐缩短为几个较短的惰行连接段，且惰行连接段数目逐渐增加，区间运行时间也随之减小；并且随着t的增大，区间运行时间减小的趋势也逐渐减缓，在t=140 m/s时，区间运行时间与最大能力运行时间已经十分接近。

在t=limit情况下得到的区间运行时间与最大能力运行时间相比，有68.09%的运行时间裕量，而地铁列车正常运营时的区间运行时间裕量一般不超过30%，可见t=limit时对应的区间运行时间裕量远远超出地铁列车实际运营时对区间运行时间裕量的要求。可见在正常区间运行时间范围情况下的计算，t的取值范围必然为t＞limit，2.1节对t取值的假设满足实际应用条件。

表5 区段划分

表6 vt=19.44 m/s的有效连接误差

4.2 算例2

采用算例1中的列车和线路数据，区间运行时间要求为111 s，采用3.4节的定时节能算法计算节能速度曲线，对应的t为64.07 m/s。对比方案为该线路列车自动驾驶系统实际采用的驾驶策略。在该运行时间条件下，对比方案采用在最大能力运行的基础上仅在停车制动前施加惰行的节能驾驶策略，惰行起点通过迭代计算得到。

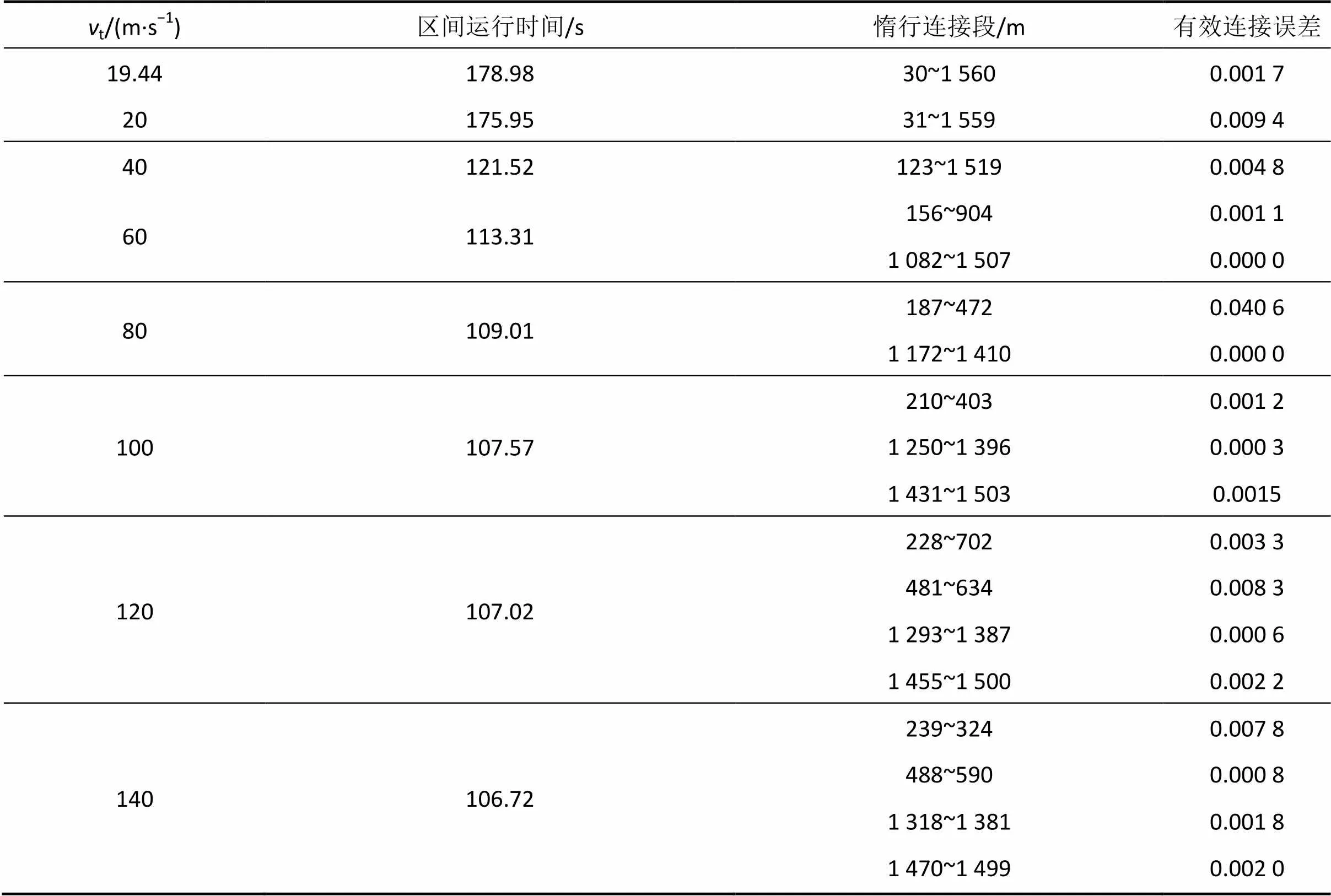
表7 区间运行时间随vt的变化情况

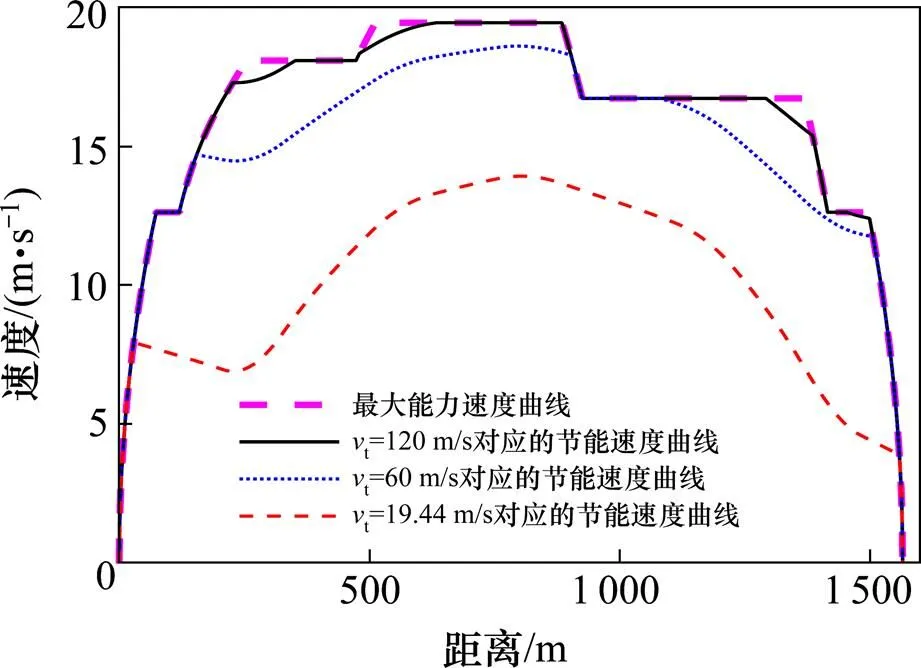
图4 算例1速度曲线计算结果

2种方案的速度曲线计算结果如图5所示，区间运行时间、惰行段和能耗如表8所示，本文算法比对比方案节能21.92%，节能效果更好。

基于本文算法计算得到的惰行连接段满足由极大值原理推导得到的最优工况切换条件，在一定的计算精度下可以获得理论上的最优解，可以认为通过该算法得到的惰行连接段为当前计算精度条件下的最优惰行连接段，能够充分利用线路条件获得最佳节能效果。

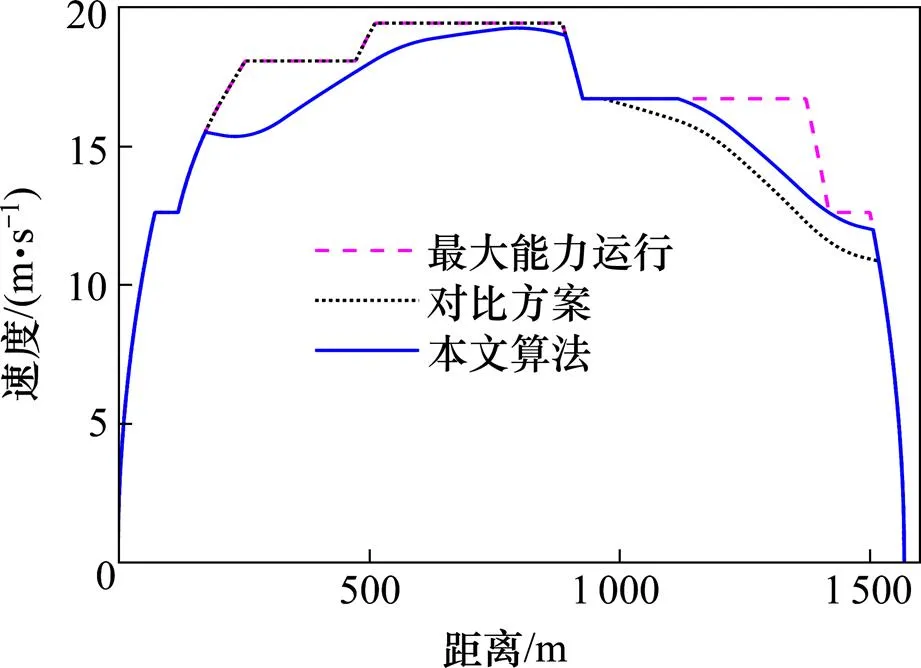
图5 算例2速度曲线计算结果

表8 不同节能策略对比

5 结论

1) 以往基于极大值原理的常规方法偏重于目标牵引恒速小于线路限速的情况下的节能驾驶分析，该情况下的牵引目标恒速能够实现且计算较为复杂；本文基于牵引目标恒速高于线路限速的假设，将给定目标牵引恒速下的地铁列车节能驾驶优化问题简化为在列车最大能力运行工况的基础上加入最节能惰行连接段的问题。

2) 基于以往研究应用极大值原理得到最优工况切换条件，构造简化情况下计算最优惰行连接段的数值算法，进而得到地铁列车定时节能速度曲线的计算方法。该简化算法避免了应用极大值原理的常规方法中对带伴随变量的微分方程组的求解过程，并且可以处理详细的列车模型和复杂的线路条件，适合工程应用。

3) 基于实际列车和线路数据对该简化方法的假设条件进行验证，计算结果表明在该假设情况下的区间运行时间范围满足地铁列车实际运行需求，证明了该假设在实际应用中的合理性；在相同的运行时间条件下，本文算法比列车目前实际采用的驾驶策略节能21.92%，证明了算法的节能性。

[1] YANG Xin, LI Xiang, NING Bin, et al. A survey on energy-efficient train operation for urban rail transit[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 17(1): 2−13.

[2] 荀径, 杨欣, 宁滨, 等. 列车节能操纵优化求解方法综述[J]. 铁道学报, 2014, 36(4): 14−20. XUN Jing, YANG Xin, NING Bin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14−20.

[3] Scheepmaker G M, Goverde R M P, Kroon L G. Review of energy-efficient train control and timetabling[J]. European Journal of Operational Research, 2017, 257(2): 355−376.

[4] Ichikawa K. Application of optimization theory for bounded state variable problems to the operation of train[J]. The Japan Society of Mechanical Engineer, 1968, 11(47): 857−865.

[5] Khmelnitsky E. On an optimal control problem of train operation[J]. IEEE Transactions on Automatic Control, 2000, 45(7): 1257−1266.

[6] LIU Rongfang, Golovitcher I. Energy-efficient operation of rail vehicles[J]. Transportation Research Part A: Policy Practice, 2003, 37(10): 917−932.

[7] Howlett P G, Pudney P J, Vu X. Local energy minimization in optimal train control[J]. Automatica, 2009, 45(11): 2692−2698.

[8] Albrecht A R, Howlett P G, Pudney P J, et al. Energy-efficient train control: from local convexity to global optimization and uniqueness[J]. Automatica, 2013, 49(10): 3072−3078.

[9] Albrecht A, Howlett P, Pudney P, et al. The key principles of optimal train control—Part 1: Formulation of the model, strategies of optimal type, evolutionary lines, location of optimal switching points[J]. Transportation Research Part B: Methodological, 2016, 94(2): 482−508.

[10] Albrecht A, Howlett P, Pudney P, et al. The key principles of optimal train control—Part 2: Existence of an optimal strategy, the local energy minimization principle, uniqueness, computational techniques[J]. Transportation Research Part B: Methodological, 2016, 94(2): 509−538.

[11] 王青元, 冯晓云, 朱金陵, 等. 考虑再生制动能量利用的高速列车节能最优控制仿真研究[J]. 中国铁道科学, 2015, 36(1): 96−103. WANG Qingyuan, FENG Xiaoyun, ZHU Jinling, et al. Simulation study on optimal energy-efficient control of high speed train considering regenerative brake energy[J]. China Railway Science, 2015, 36(1): 96−103.

[12] 王青元, 冯晓云. 列车准点节能运行的控制工况最优切换研究[J]. 中国铁道科学, 2016, 37(2): 91−98. WANG Qingyuan, FENG Xiaoyun. Optimal switching for control conditions of punctual and energy efficient operation of train[J]. China Railway Science, 2016, 37(2): 91−98.

[13] 梁志成, 王青元, 何坤, 等. 基于极大值原理的电动车组节能操纵[J]. 铁道学报, 2015, 37(10): 16−25. LIANG Zhicheng, WANG Qingyuan, HE Kun, et al. Energy saving control of electric multiple unit train based on maximum principle[J]. Journal of the China Railway Society, 2015, 37(10): 16−25.

[14] 陈荣武, 刘莉, 郭进. 基于遗传算法的列车运行能耗优化算法[J]. 交通运输工程学报, 2012, 12(1): 108−114. CHEN Rongwu, LIU Li, GUO Jin. Optimization algorithm of train operation energy consumption based on genetic algorithm[J]. Journal of Traffic and Transportation Engineering, 2012, 12(1): 108−114.

[15] 黄友能, 宫少丰, 曹源, 等. 基于粒子群算法的城轨列车节能驾驶优化模型[J]. 交通运输工程学报, 2016, 16(2): 118−124. HUANG Youneng, GONG Shaofeng, CAO Yuan, et al. Optimization model of energy-efficient driving for train in urban rail transit based on particle swarm algorithm[J]. Journal of Traffic and Transportation Engineering, 2016, 16(2): 118−124.

[16] YIN Jiateng, CHEN Dewang, LI Lingxi. Intelligent train operation algorithms for subway by expert system and reinforcement learning[J]. IEEE Transactions on Transportation Systems, 2014, 15(6): 2561−2571.

[17] 石红国, 彭其渊, 郭寒英. MRT列车运行模拟模型的多目标改进遗传算法[J]. 西南交通大学学报, 2006, 41(5): 658−662. SHI Hongguo, PENG Qiyuan, GUO Hanying. Improved multi-objective GA for MRT train operation simulation model[J]. Journal of Southwest Jiaotong University, 2006, 41(5): 658−662.

[18] Adrián F, Antonio F, Asunción P Cucala, et al. Design of robust and energy-efficient ATO speed profiles of metropolitan lines considering train load variations and delays[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 2061−2071.

[19] Sandidzadeh M A, Alai M R. Optimal speed control of a multiple-mass train for minimum energy consumption using ant colony and genetic algorithms[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2017, 231(3): 280− 294.

[20] 贺德强, 周继续, 李宇轩, 等. 基于矩阵离散法的地铁列车节能优化操纵方法及实现[J]. 铁道学报, 2015, 37(7): 9−14. HE Deqiang, ZHOU Jixu, LI Yuxuan, et al. Energy saving optimization operation method for metro train based on matrix discrete method and its implementation[J]. Journal of the China Railway Society, 2015, 37(7): 9−14.

[21] 柏赟, 周雨鹤, 邱宇, 等. 长大下坡道区间地铁列车节能操纵方法[J]. 中国铁道科学, 2018, 39(1): 108−115. BAI Yun, ZHOU Yuhe, QIU Yu, et al. Energy-efficient control method for subway train in section with long heavy down grade[J]. China Railway Science, 2018, 39(1): 108−115.

[22] 刘炜, 王栋, 李群湛, 等. 基于时间逼近搜索算法的城轨列车运行节能优化研究[J]. 西南交通大学学报, 2016, 51(5): 918−924. LIU Wei, WANG Dong, LI Qunzhan, et al. A novel time-approaching search algorithm for energy-saving optimization of urban rail train[J]. Journal of Southwest Jiaotong University, 2016, 51(5): 918−924.

[23] SU Shuai, TANG Tao, CHEN Lei, et al. Energy-efficient train control in urban rail transit systems[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2015, 229(4): 446− 454.

[24] GU Qing, TANG Tao, CAO Fang, et al. Energy-efficient train operation in urban rail transit using real-time traffic information[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(3): 1216−1233.

[25] 陶生桂, 王曰凡, 毛明平. 上海地铁2号线牵引仿真计算研究[J]. 城市轨道交通研究, 2001, 4(2): 22−27. TAO Shenggui, WANG Yuefan, MAO Mingping. Digital simulation calculation method in vehicle traction of Shanghai metro line 2[J]. Urban Mass Transit, 2001, 4(2): 22−27.

A simplified algorithm of energy-efficient driving for metro trains based on the Maximum Principle

QU Jianwei, WANG Qingyuan, SUN Pengfei

(School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China)

An assumption that the target traction cruising speed is higher than the speed limits was introduced in the problem of energy-efficient driving optimization for metro trains within a given runtime. The energy-efficient driving regime set and the timing of using such regimes, derived from earlier analyses based on the Maximum Principle method, were simplified; and the problem of calculating the energy-efficient speed curve under a given target traction cruising speed was also further simplified as a problem of finding the optimal coasting segments based on the traction and braking regimes of the flat-out run. The section between two stations were divided into different segments based on the results of the flat-out run, and the connection function and connection error were introduced to describe the connection effect of the coasting regime. Based on the switching rules of optimal driving regimes, a numerical algorithm for calculating the optimal coasting segments under a target traction cruising speed was proposed, and an algorithm for calculating the optimal energy-efficient speed curve with the given section runtime was further constructed. The actual data of Harbin metro line 3 were used to verify the algorithm. The results confirm the feasibility of the hypothesis, suggesting that as much as 21.92% energy can be saved when the algorithm is used, compared with the current driving strategy of the train.

metro train; energy-efficient driving; the Maximum Principle; switching rules of driving regimes; connection function

U231.6

A

1672 − 7029(2019)06− 1577 − 10

10.19713/j.cnki.43−1423/u.2019.06.030

2018−09−19

国家重点研发计划资助项目(2016YFB1200502)

王青元(1984−)，男，江苏盐城人，高级工程师，从事列车运行优化控制理论与技术、列车运行仿真及其工程应用研究；E−mail：wangqy@swjtu.edu.cn

(编辑 蒋学东)