多边形第三外角和统一性研究*

广东省中山市民众中学(528441)杨良畏

1 背景介绍

数学教材关于多边形外角及外角和知识,基本上围绕凸多边形定义,很少看到有关凹多边形外角及外角和定义的内容.笔者查阅很多资料,但没有得到一个大家公认的确切的定义.有不少研究者对此问题作出研究,如文献[1]对凹多边形外角定义是根据内角是否为凹角和凸角(凹角和凸角定义见文献[2])来定义.在文献[3]中,黄灿军直接对文献[1]提出质疑,该文认为凹多边形外角定义同凸多边形外角定义,在计算时运用了张景中院士《数学家的眼光》“方向改变量之和”代替“外角和”思维,得到凹多边形外角和为360°.在文献[2][4]中,作者均认为凹多边形外角和大于360°.这些“定义”都有一定的道理,但没有一个像多边形内角和那样完美统一结论(凹凸n边形的内角和是完美统一结构,均为(n-2)×180°.).

笔者曾在文献[5]中给出多边形外角和另类定义,得到多边形第二外角和及多边形第三外角和.这两种外角和是针对凸多边形进行定义.笔者发现多边形第三外角和可以推广到凹多边形,得到一个完美且统一的定理.

定理1n边形第三外角和为(n+2)×180°.

此定理中多边形指的不仅仅是凸多边形,且在凹多边形情况下也成立.笔者在文献[5]中已经阐述了多边形第三外角和产生的原因,给出凸n边形第三外角和为(n+2)×180°结论.若多边形外角定义依据文献[5],并得到读者认同.则定理1 可以改述为:n边形外角和为(n+2)×180°.这就同内角和一样将多边形的外角和统一起来,且具有数学美感,并易于理解.

2 相关知识介绍

为了证明定理1,需作一些准备工作.

定义1内角中至少有一个大于180°的多边形称为凹多边形.

凹多边形还可以定义为:如果多边形的所有边只要有一条边向两方无限延长成为一直线时,其他边不在此直线的同旁,那么这个多边形就叫做凹多边形.凹多边形至少需要四条边才可以构成.如图1就是一个凹四边形.

定义2凹多边形中大于180°的内角,称为凹多边形的凹角.小于180°的角称为凹多边形的凸角[2].

如图1,∠3就是凹角,∠1∠2∠4 是凸角.

图1

笔者在文献[5]中,将传统的外角和称之为外角和第一定义,简称第一外角和.在给出邻组角概念后,重新定义了(凸)多边形的外角.

定义3如果两个角相加等于360°,并且两个角的边相互重合,那么称这两个角为邻组角.

定义4多边形内角的邻组角称为多边形的外角.

这个定义区别于外角传统定义,而且在数量上也是完全不一样.如图2,顶点A对应∠1 和∠2 两个角,其中∠1 是内角,∠2 是笔者定义的外角.

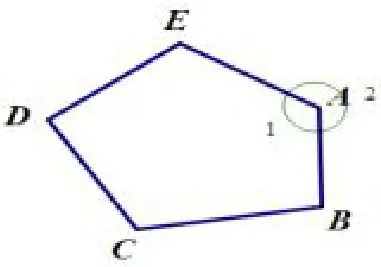
图2

这里的外角定义很“外角”,完全就是多边形的外面的角.由图2可知:五边形的外角是两个传统的外角加上与其对应的内角之和.所以我们得到五边形的外角和第三定义(简称为第三外角和),五边形第三外角和为720°+540°=1260°.由此我们可以推出n边形的第三外角和为(n+2)×180°.这与n边形的内角和为(n-2)×180°有些相似.其实这种定义可以推广到凹多边形中,如图1中,∠3 的邻组角∠5 称为凹多边形的外角.文献[1][2]对凹多边形中凹角对应的外角定义同于笔者定义,只是两文作者对凹多边形中凸角的外角定义同于凸多边形外角定义.这种区别对待方式有点牵强,会让读者有云雾之感.笔者文中外角定义一视同仁,不管凹凸,外角均指其内角对应的邻组角.

文献[2]给出凹n边形外角定义,且得到如下两个重要命题.

命题1凹n(n≥4)边形最少有一个凹角,最多有(n-3)个凹角.

命题2有q(1 ≤q≤n-3)个内角为凹角的任意凹n(n≥4)边形的外角和为(q+2)×180°.

3 定理1 的证明

由于凸n边形第三外角和等于(n+2)×180°显然成立,本文不再赘述.下面将详述证明凹n边形第三外角和等于(n+2)×180°.

证明设凹n(n≥4)边形有q(1 ≤q≤n-3)个内角为凹角,则有(n-q)个凸角.因为文献[2] 中凸角对应外角的定义与多边形第三外角定义相差180°.故(n-q)个凸角相差(n-q)×180°.由命题2 知有q(1 ≤q≤n-3)个内角为凹角的任意凹n(n≥4)边形的第三外角和为:(q+2)×180°+(n-q)×180°.化简后得:(n+2)×180°.证毕.

也就是说凹n(n≥4)边形第三外角和等于(n+2)×180°.它与凹角的个数无关,仅与多边形的边数有关.从而得到:n边形第三外角和为(n+2)×180°.

4 小结

由此,不难发现笔者另类定义的多边形第三外角不仅适用于凸多边形,而且对凹多边形也适用.它的优越性体现在两点.一是突出几何直观视觉,且具有稳定性,不会因凹凸变化而变化定义.二是具有统一性,它将凹凸多边形外角和统一为(n+2)×180°.这与凹凸多边形内角和(n-2)×180°相对应,具有数学美感!