大姿控力矩复合控制导弹制导控制一体化设计*
毛柏源,李君龙,张锐,叶松青
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团有限公司 第二研究院,北京 100854;3.中国船舶工业物资东北有限公司,辽宁 沈阳 110011)
0 引言
对于传统拦截弹的制导控制系统设计,普遍采用将制导与控制回路分别单独设计的方法,这种方法是基于频谱分离的假设,而在拦截大机动目标时,导弹制导回路的时间常数比较小,带宽随之变大,此时频谱分离的假设不再成立,通常会导致拦截弹末制导段脱靶量较大,为解决此问题,制导控制一体化技术应运而生。
制导控制一体化是将导弹制导回路与控制回路整合为一个回路,充分考虑了两回路之间的耦合,根据弹目相对运动信息与弹体姿态运动信息,直接产生控制指令,既能减少制导与控制两回路间的延迟,同时能减少控制系统设计周期和成本。
自从Williams[1]首次提出制导控制一体化设计后,国内外大量学者对导弹制导控制一体化设计方法进行了研究。文献[2-4]对于机动目标的拦截问题,采用滑模控制方法研究了制导控制一体化算法,并且考虑了模型不确定性。文献[5]针对控制输入饱和问题,采用自适应动态面反步法设计一体化控制器。文献[6]基于小增益理论研究了复合控制导弹的制导控制一体化设计,该算法适用于机动性较差的目标。文献[7]针对弹目视线角速率与导弹攻角都无法测量的拦截情形,研究了一种基于部分状态反馈的一体化控制律。对于末制导攻击角度约束场景,郭超等[8]将攻击角约束转化为终端视线角约束问题,提出一种基于反演滑模与扩张状态观测器的制导控制一体化设计方法。文献[9]基于自适应动态面的反步法研究了三维拦截空间的制导控制一体化设计方法。目前,制导控制一体化的相关研究大都是采用单一执行机构的控制对象,而对于直/气复合控制的制导控制一体化研究较少。
本文针对制导控制一体化在直气复合控制导弹上的应用进行相关研究,首先建立了拦截弹直/气复合控制的制导控制一体化模型,针对目标机动信息未知、存在建模误差等干扰量,采用有限时间收敛的非线性干扰观测器补偿未知信息,之后基于动态面的反步法设计了一体化控制律,最后通过与传统制导与控制分开设计的方法进行仿真对比,结果表明,本文设计的一体化控制律使得末制导段脱靶量更小,具有更高的制导精度。
1 模型建立
为提高拦截弹高空机动能力同时减小末制导段脱靶量,本文研究了一种基于大姿控力矩直/气复合控制的制导控制一体化设计方法。该方法中的直接侧向力与气动舵共同构成姿控模式的直/气复合控制形式。
直接力的建立过程如图1所示,其中,Fmax代表稳态推力,T0代表直接力机构开机延迟,ΔT代表关机延迟。

图1 直接侧向力推力特性Fig.1 Thrust characteristic of lateral force
复合控制拦截弹俯仰通道数学模型如下[10]
(1)

对于本文研究的拦截弹直/气复合控制模型,考虑将直接力F引入后,定义直接力产生等效舵偏角为
(2)
式中:δmax为气动舵偏角限幅值。
则建立等效弹体模型,令δz=δp=δ,式(1)可写为
(3)
为了研究方便,本文将末制导段的拦截空间解耦为2个二维平面。将导弹和目标视为质点,在纵向平面内,弹目相对运动关系如图2所示,图中M,T分别为导弹和目标;vM,vT分别为导弹和目标的速度;aM,aT分别为导弹和目标的法向加速度;θM,θT分别为导弹和目标的航迹角;R为弹目相对距离;q为视线角。在极坐标系下建立弹目相对运动方程:
(4)
(5)
(6)
(7)

图2 弹目相对运动关系示意图Fig.2 Relative motion geometry of missile and target
将式(5)对时间求导,并结合式(4),(6),(7)得到
(8)
忽略偏航和滚转通道的影响,得到
(9)
不失一般性,本文的研究基于如下假设:
假设1在末制导过程中,认为导弹发动机停止工作且不考虑重力影响。
假设2认为在末制导阶段,导弹与目标速度大小不变。
假设3不考虑导弹舵面产生的升力。
根据以上假设,将目标机动信息、通道间耦合因素、气动参数摄动等视为外界干扰,结合式(3),(8),(9)得到复合控制导弹制导控制一体化数学模型[11]:
(10)
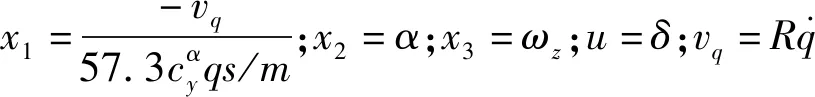
其他相关函数表达式为
(11)
式中:dvq为目标机动加速度信息;dα及dωz分别为攻角及角速率通道的未知干扰。
假设4对于系统式(10),未知干扰均有界,即
(12)
显然,系统式(10)为一个带有不确定参数的具有级联形式的非线性系统,本文制导控制一体化设计的目标是使拦截弹命中目标,并同时保证弹体姿态的稳定。
2 复合控制导弹制导控制一体化设计
2.1 制导控制一体化设计
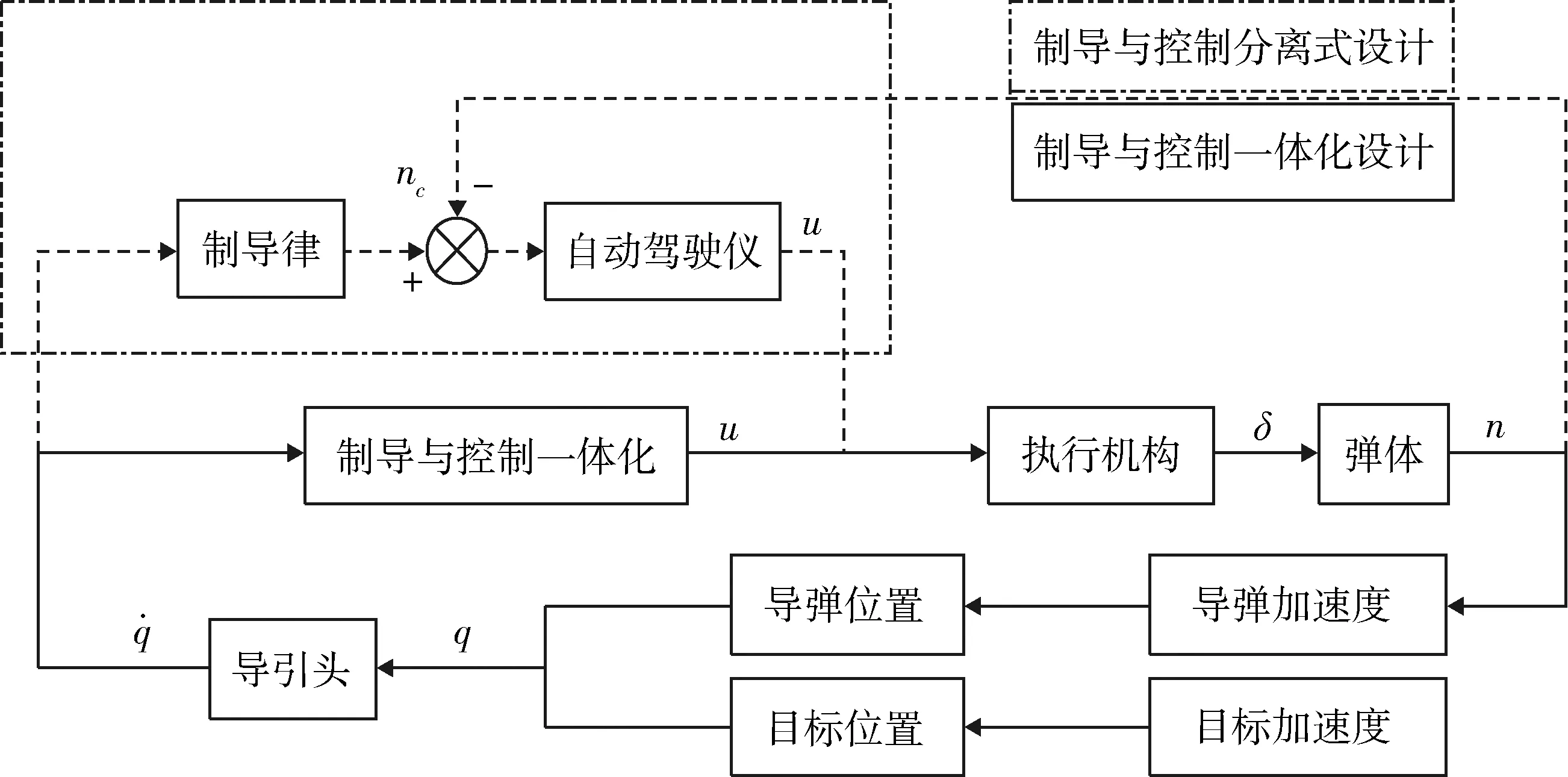
拦截弹的制导控制一体化设计通常是将制导回路与控制回路融合为一个回路,充分利用了制导与控制系统之间的耦合,有效减小了指令的时间延迟。控制系统框图如图3所示。
本文针对式(10)建立的非线性系统,采用有限时间收敛的非线性干扰观测器估计系统中的未知干扰量,并基于动态面的反步法设计制导控制一体化控制器。为简化设计过程,首先给出如下引理。
引理1[12]设在原点领域U⊂Rn上存在连续正定函数V(t),假设有实数a1,a2>0,0<γ<1使得式(13)成立
(13)
式中:t>t0,t0为系统初始时刻,则函数V(t)可在有限时间tf内收敛至0,并且收敛时间满足:
(14)
对于闭环系统式(10),为设计干扰观测器,引入如下辅助变量:
si=zi-xi,i=1,2,3.
(15)
根据文献[13],zi设计为
(16)
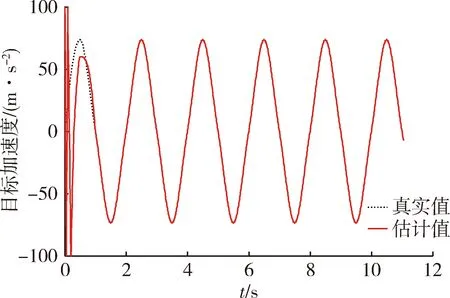
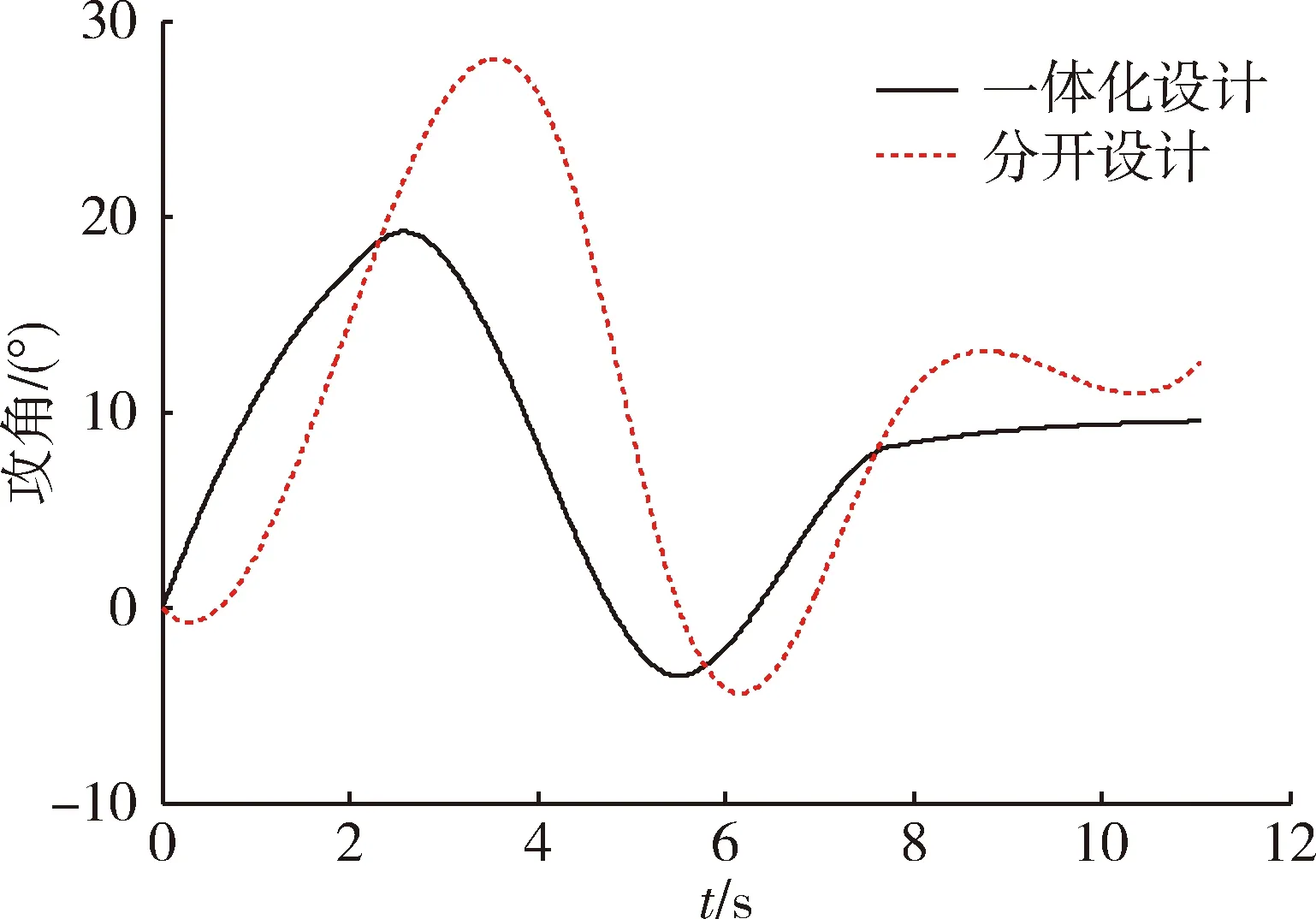
式中:ki>0;ηi>0;ρsi=pi/qi,pi,qi为正奇数,且pi |fi(xi)|sign(si)-fi(xi). (17) 对式(15)求微分,并结合式(10),(16),得到 |fi(xi)|sign(si)-fi(xi)-di. (18) 设观测器误差为 (19) 选取Lyapunov函数 (20) 结合式(18)有 |fi(xi)|sign(si)-fi(xi)-di)= |fi(xi)||si|-fi(xi)si-disi. (21) 显然 (22) 则式(21)可写为 (23) 根据引理1可知,si在有限时间收敛到0。 将式(17),18)代入式(19),得到观测器误差: (24) 由si的有限时间收敛特性可知,干扰的估计误差εi也将在有限时间收敛到0。 基于动态面的反步法设计的制导控制一体化控制器设计步骤如下[14]: 第1步:针对式(10)第1式定义第1个误差面 e1=x1-x1d, (25) 式中:x1d为系统式(10)第1个公式的期望指令信号。将式(25)对时间求导,并结合式(10)第1式得 图3 制导与控制一体化框图Fig.3 Block diagram of integrated guidance and control (26) 则虚拟控制量可设计为 (27) (28) 设第1个虚拟控制量的滤波误差为 (29) 第2步:针对式(10)第2式定义第2个误差面 (30) 将式(27),(29)和(30)代入式(26)可得 (31) 式(30)对时间求导,并结合式(10)第2式得 (32) 则虚拟控制量可设计为 (33) (34) 设第2个虚拟控制量的滤波误差为 (35) 第3步:针对式(10)第3式定义第3个误差面 (36) 将式(33),(35)和(36)代入式(32)可得 (37) 式(36)对时间求导,并结合式(10)第3式得 (38) 则系统的实际控制量设计为 (39) 将式(39)代入式(38)可得 (40) 至此,导弹制导控制一体化设计完成,式(39)即为系统最终设计的一体化制导控制律。 定理1对于非线性系统(10),若采用如式(39)的控制量,以及如式(27),(33)的虚拟控制量,则可以使整个系统稳定。 证明针对系统式(10)构造如下的Lyapunov函数 (41) 对该Lyapunov函数求导得 (42) 根据式(31),(37)和(40),可得 e2(e3-e1-m2e2+n2+ε2)+ e3(-e2-m3e3+ε3)= (43) 根据式(29),(35)可得 (44) 将式(43),(44)代入(42)可得 (45) 应用Young不等式[15]:ab (46) 将式(46)代入(45)可得 (47) 求解式(47),可得 (48) 所以V(t)最后会收敛到一个界限为λ/c0的邻域内,即闭环系统的所有状态均可收敛到原点附近任意小的邻域内。 针对第1节建立的复合控制导弹制导控制一体化模型,本节将对某拦截弹末制导段进行数学仿真。仿真步长取为0.001 s,从末制导时刻开始,机动目标的初始位置为(200,20) km,目标速度为vT=1 800 m/s,目标执行正弦机动,机动加速度为aT=7.5gsin(πt) m/s2,且目标加速度极限值为aTmax=100 m/s2。导弹的飞行状态参数如表1所示。导弹的初始位置为(170,18) km,初始姿态角和初始姿态角速度均设为0。导弹各气动系数与直接力系数如下: 表1 导弹飞行状态参数Table 1 Flight state parameters of missile 为验证本文设计的制导控制一体化控制律的有效性,使用传统制导控制系统单独设计方法进行对比,仿真结果如图4~9所示。 为更好地验证本文所设计方法的有效性,取3种拦截情形进行对比。仿真初值如表2所示。 图4 视线角速率曲线Fig.4 Curves of line of sight angular rate 图5 目标加速度估计Fig.5 Estimation of target maneuver 图6 攻角曲线Fig.6 Curves of angle of attack 图7 舵偏角曲线Fig.7 Curves of rudder deflection 图8 弹目相对距离Fig.8 Relative distance of missile and target 图9 拦截过程脱靶量变化曲线Fig.9 Miss distance curves of intercepting process 表2 仿真初值Table 2 Initial values of the simulation 3种拦截情形下的拦截时间与脱靶量统计如表3所示。 表3 仿真结果Table 3 Simulation results 由图4可得出,本文设计的制导控制一体化控制律能够使视线角速度迅速收敛到零附近,而采用传统制导方法时视线角速度收敛过程随着目标机动存在较大波动,说明本文所提出算法相对传统设计方法具有更优良的性能。由图6,7可知,采用一体化控制器得到的攻角与舵偏角曲线相对于制导与控制分开设计时更加平稳。根据表3可知,在多种拦截情形下,采用一体化设计得到的脱靶量均小于传统制导与控制分开设计得到的结果。可见,本文设计的制导控制一体化控制器具有更高的制导精度。 本文基于动态面的反步法设计了复合控制导弹制导控制一体化控制律,采用有限时间收敛的非线性干扰观测器估计与补偿了系统中不确定信息,有效提升了控制器的鲁棒性。从仿真结果可以看出,相比于传统制导与控制分开设计的方法,本文提出的一体化控制律具有更高的制导精度与更优良的性能。
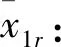

2.2 系统稳定性分析

3 仿真校验







4 结束语

