MLICP-CNN：基于CNN与ICP的多标记胸片置信诊断模型

吴能光 王华珍* 许晓泓 刘俊龙 何 霆 吴谨准

1(华侨大学计算机科学与技术学院 福建 厦门 361021)2(厦门大学附属第一医院儿科 福建 厦门 361003)

0 引 言

X线胸片(Chest X-ray)是辅助诊断肺部相关疾病的医学影像。胸片能同时展示肺部炎症、肿块、肺结核、气胸等一种或多种医学病理特征，因此胸片诊断是典型的多标记问题。2017年，美国国立卫生研究院开源了数据量巨大且多标记标注的胸片数据集Chest X-ray14[1]，胸片多标记诊断开始引起学界广泛关注。Haloi等[2]提出基于卷积神经网络的在线增强分类网络来辅助胸部疾病诊断。Boosted等[3]基于深度卷积神经网络定义了全新的损失函数来处理多标记和不平衡的胸片数据集。Abiyev等[4]对比了多种神经网络模型(卷积神经网络、反向传播神经网络、无监督学习神经网络)的胸部疾病诊断性能。但这些研究仅仅是传统多标记模型在胸片诊断问题上的应用，并没有考虑胸片诊断的高风险特性。胸片诊断属于典型的高风险领域，诊断失败将导致严重的后果。这需要诊断模型能对输出结果附带置信度评估，以确保足够的安全保障。另 外，临床上需要对单个患者进行独立的风险评估，而非通过统计运算获得。总之，多标记胸片置信诊断模型研究具有重要的现实和学术价值。

对于上述情况，本文提出一种基于卷积神经网络[5]与归纳一致性预测器[6]的多标记胸片置信诊断模型MLICP-CNN。该模型能为每个被测数据提供附带置信度的预测集，并且其置信度是可校准的。MLICP-CNN模型将学习数据划分为训练集和校准集，通过使用CNN从训练样本中学习出规则D，基于D和校准集使用算法随机性对被测数据进行置信预测。规则D利用CNN高度特征抽取能力有效提取了训练集中的信息，从而提升了模型的预测效率。通过算法随机性检验把被测数据的预测问题转化成学习数据集分布的统计检验问题，其置信度评估具有统计意义的理论可校准性。

本文的主要贡献如下：

1) 提出MLICP-CNN模型，能提供可校准的多标记置信预测。

2) 设计类别敏感的样本奇异值函数，能根据样本类别自适应测量奇异值，提升预测效率。

3) 关注胸片数据集Chest X-ray14的高风险特性，引入置信机制。

1 相关工作

1.1 基于CNN的胸片诊断模型研究

通过X线胸片来诊断肺部等疾病极具挑战性，为了克服人类的认知偏倚和效率低下等局限性，X线胸片智能辅助诊断模型研究成为众多学者的研究对象。其中最具代表性的是基于CNN的诊断模型研究。CNN是一种卷积层与采样层交替设置的多层神经网络。卷积层使用局部权值共享机制提取不同角度的局部特征。采样层能进行有效的特征抽象。CNN的局部特征提取和高层次特征抽象能避免对图像复杂的特征提取和数据重建过程，可以直接输入原始图像，尤为适用于图像模式辨识问题，因此，在胸片诊断领域获得较为广泛的应用。

不同学者针对胸片诊断的具体问题设计了不同的CNN模型，Rajpurkar等[7]则提出基于121层稠密卷积神经网络(Densent-121)并采用二元交叉信息熵作为损失函数来构建胸片肺炎诊断模型。Dong等[8]对比vgg16和ResNet-101等多种卷积神经网络模型来确定胸片异常检测的最优模型。Qin等[9]采用4层卷积神经网络对胸片做分割任务。

2017年，开源的Chest X-ray14[1]数据集不仅数量巨大并且每张胸片对应一个或多个标签，引发学术界对多标记胸片模型的研究。目前，对Chest X-ray14数据集多标记学习问题的研究思路大多采用二元相关方法，将数据集分解为14个单标记问题，进而分别进行模型构建和AUC性能评估。典型的工作有Wang等[1]的研究，但其模型性能表现欠佳。Baltruschat等[10]对比了多种深度学习方法在Chest X-ray14数据集的多标记分类评估性能。Cai等[11]在CNN中引入注意力机制，从而提升模型对疾病类型的敏感性和显著性。以上研究虽然考虑了胸片诊断的多标记特性，但还没有考虑到胸片诊断的高风险特性。

1.2 基于ICP的置信预测

在ICP框架中，被测数据的预测问题转化成学习数据集分布的统计检验问题。具体地，ICP使用算法随机性检验对被测数据进行预测，采用置信度作为预测结果的风险评估。ICP是CP[12]理论的修正模型，其与CP的区别在于预先将学习样本划分为训练集和校准集，使用归纳推理从训练样本中学习出规则D，进而基于D和校准集使用算法随机性检验对被测数据进行置信预测。

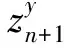
(1)

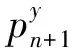
(2)

(3)

满足式(3)称为置信预测具有可校准性[13]。

当面对大数据学习问题时，ICP能提高运算效率，其算法示意图如图1所示。

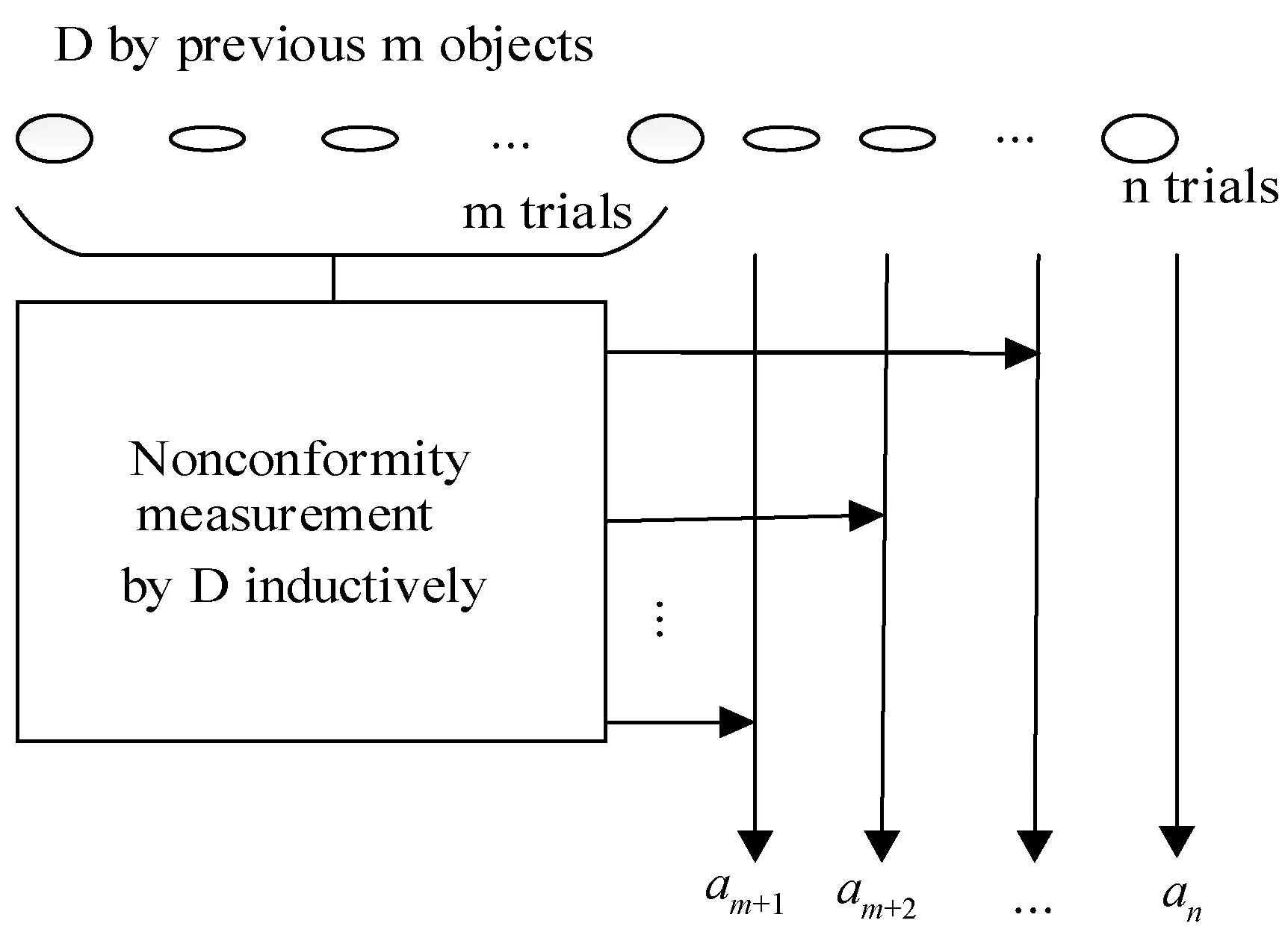
图1 ICP算法示意图

图1中，学习样本中的前m个用于构建规则D，剩余n-m+1个样本利用规则D来计算样本奇异值ai,i=m+1,m+2,…,n。可见，ICP以规则D为传递媒介将所有学习样本都参与到置信预测中，从而保证了被测数据的可校准性。

2 MLICP-CNN算法原理

本文提出的MLICP-CNN算法以ICP框架为核心，将学习数据划分为训练集和校准集，对应地分为归纳推理和置信预测两个阶段。已知多标记学习数据集为Zn={z1,z2,…,zn}，单个被测数据xn+1。数据集Zn被分割成训练集为Zm={z1,z2,…,zm}和校准集Zv={zm+1,zm+2,…,zn}，m+v=n。MLICP-CNN算法示意图如图2所示,Zm用于训练卷积神经网络模型，Zv作为校准集参与xn+1的置信预测。

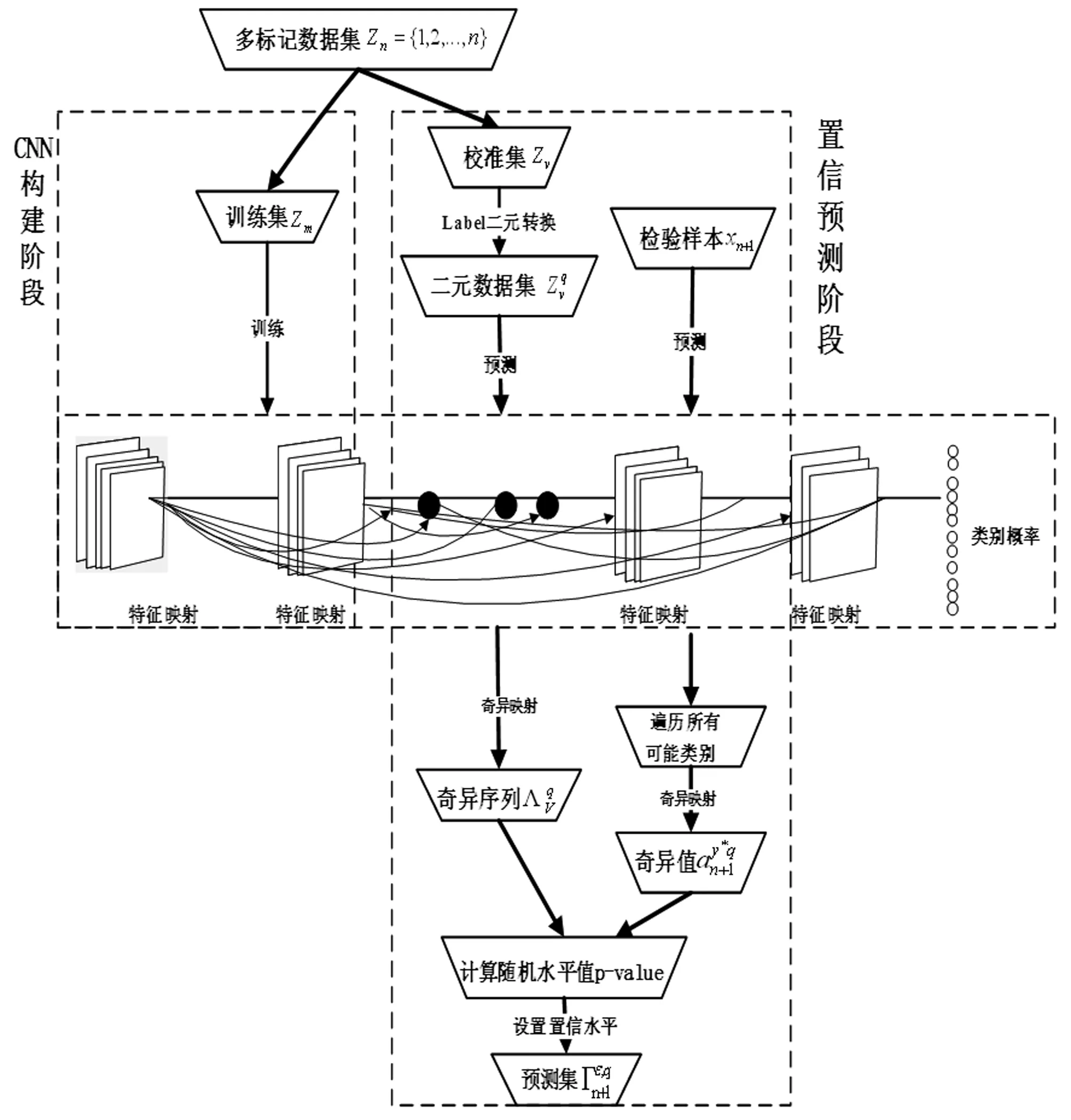
图2 MLICP-CNN算法示意图

2.1 CNN构建阶段

本阶段属于归纳推理阶段，对训练样本进行卷积神经网络CNN模型构建，即CNN模型为规则D。

CNN是一个多层的神经网络，包括嵌入层、卷积层、池化层、全连接层四个部分。CNN通过输入层的卷积计算，每块局部的输入区域链接一个输出神经元。

运用不同卷积计算可以形成多通道输出，进而通过池化层采样，最后汇总输出结果。CNN能够进行样本特征的自动、多层次和多角度提取，具有良好的建模能力。

针对多标记数据集，CNN将多标记标签集作为网络的输出层结果，即输出层有多个真实标签。在训练多标记数据集时，我们采用二元交叉熵损失来定义损失函数：

(1-θq)logp(Tq=0|X))]

(4)

式中：q∈{1,2,…,Q}类别，p(Tq=1|X)表示包含类别q的概率，p(Tq=0|X)表示不包含类别q的概率。θq表示类别q是否存在即θq∈{1,0}。

2.2 置信预测

在置信预测阶段，我们利用CNN模型来获取被测样本序列每个样本的奇异值，进而在指定风险水平下产生多标记预测集。该预测集附带了置信度作为预测结果的风险评估水平。置信预测的算法思想具体包含以下几个方面：

2.2.1基于二元标记的模式转换

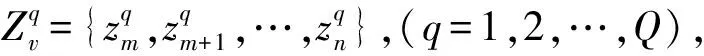
2.2.2奇异映射

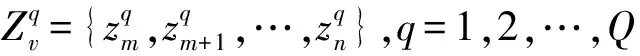
(5)

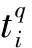
为了充分利用校准集的信息，可以进一步将校准集数据的真实标签融入奇异值函数设计中，因此可设计出另一个奇异值函数，如下式所示：

(6)

上述公式可以根据校准集样本的真实标签修正CNN输出的类概率，使得类概率更接近真实值，从而获得更小的奇异值来修正校准集样本中每个样本的离群性。

综上所述，我们将基于式(5)的模型称为MLICP-CNN，而将采用式(6)的模型称为类别敏感MLICP-CNN(记为LS-MLICP-CNN)。

2.2.3随机水平P值

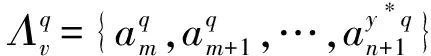
(7)

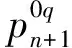
2.2.4置信输出

(8)

基于以上算法原理，本文提出的MLICP-CNN算法流程如算法1所示。

算法1 MLICP-CNN算法输入:多标记数据集Zn={z1,z2,…,zn}和单个被测数据xn+1,风险评估水平ε输出:预测标记集Γεn+1① 数据划分把Zn={z1,z2,…,zn}集划分为训练集Zm和校准集Zv,其中m+v=n;zi=(xi,Yi={yq,q=1,2,…,Q})② 模式转化多标记校准集Zv转换成Q组单标记二分类数据集Zqv={zqm,zqm+1,…,zqn}(q=1,2,…,Q),即for q=1 to Q do zqi=(xi,yqi),yqi∈(0,1)③ CNN模型训练使用Zm数据通过式(4)训练卷积神经网络D。④ 奇异映射for q=1 to Q do对校准集使用式(5)或式(6)计算每个二分类问题检验样本集的奇异值序列Λqv={aqi,i=m+1,…,n};for q=1 to Q do对xn+1 利用式(5)计算奇异值a0qn+1和a1qn+1。⑤ 计算随机水平值(P-value)for q=1 to Q do根据式(7)计算出xn+1的随机水平值p1qn+1和p0qn+1⑥ 域预测for q=1 to Q do根据式(8)计算出xn+1的预测集Γε,qn+1EndΓεn+1={∪Γε,qn+1,q=1,2,…,Q}

3 实 验

3.1 数据集

本文使用的Chest X-ray14[1]数据集属于公开发布的开源数据集，该数据集采集自30 805 名患者的正面X线胸片，数据集规模为 112 120 张。每张X 线胸片图像对应一个或多个标签，涵盖了14 种病理(肺不张、变实、浸润、气胸、水肿、肺气肿、纤维变性、积液、肺炎、胸膜增厚、心脏肥大、结节、肿块、疝气)。整个胸片数据集被划分成训练集(70%)、校准集(20%)和测试集(10%)。我们进一步将图片数据放缩到224×224，并对图片进行了均值和方差化，并通过随机水平翻转扩增每部分的样本量。

在此基础上，Chest X-ray14数据集的训练集设置为MLICP-CNN的训练集，用于训练CNN模型。而校准集则用于MLICP的置信预测阶段，测试集为本实验的测试集。

3.2 CNN参数设置

我们使用DenseNets-121[14]、DenseNets-169[14]、Resnet-50[15]三种不同架构来训练CNN模型。每个架构的全连接输出层维度由标准的1 000替换为14，并采用非线性 sigmoid 函数作为输出函数。三种架构对其他参数的设置全部相同：权重随机初始化，采用Adam[16]进行优化(选用的参数是：β1=0.9 和β2=0.999)。批量数据大小为32，初始学习速率设置为0.01。

3.3 评价指标

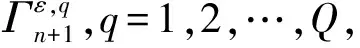
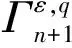
2) 确定预测率(certain prediction)：指的是输出域只含一个预测值的比率。

3) 空集率(empty prediction)：指的是输出域为空集的比率。

4) 理想预测率(favorite prediction)：指的是输出域只含一个预测值、并且该值是正确的比率。

3.4 实验结果

3.4.1置信度的可校准性展示

可校准性指的是在指定算法风险水平ε(其对应的置信度为1-ε)下，预测正确率是大于或等于对应的置信度1-ε。图3展示不同模型的可校准性，横坐标代表置信度，纵坐标代表准确率。

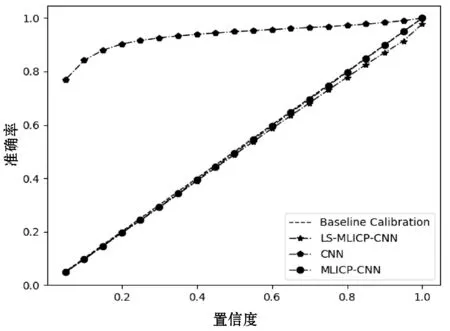
图3 对比不同模型的可校准性

在图3中，对角线称为基准线，表示准确率严格等于置信度值，在这种情况下，其置信度评估称为恰好有效。由图3可见，在各种不同的置信度下，LS-MLICP-CNN 的准确率基本等于置信度，MLICP-CNN的准确率严格等于置信度，说明本文提出的算法恰好有效。而CNN的准确率都大于置信度，则说明CNN的类概率评估不具有严格校准性。

3.4.2 预测效率展示

根据ICP理论，规则D和样本奇异值函数的设计会影响预测效率[5]，因此我们对这两种因素进行检验。本实验分别在临床常用的95%和98%置信度条件下对算法的预测效率进行展示，结果如表1和表2所示。

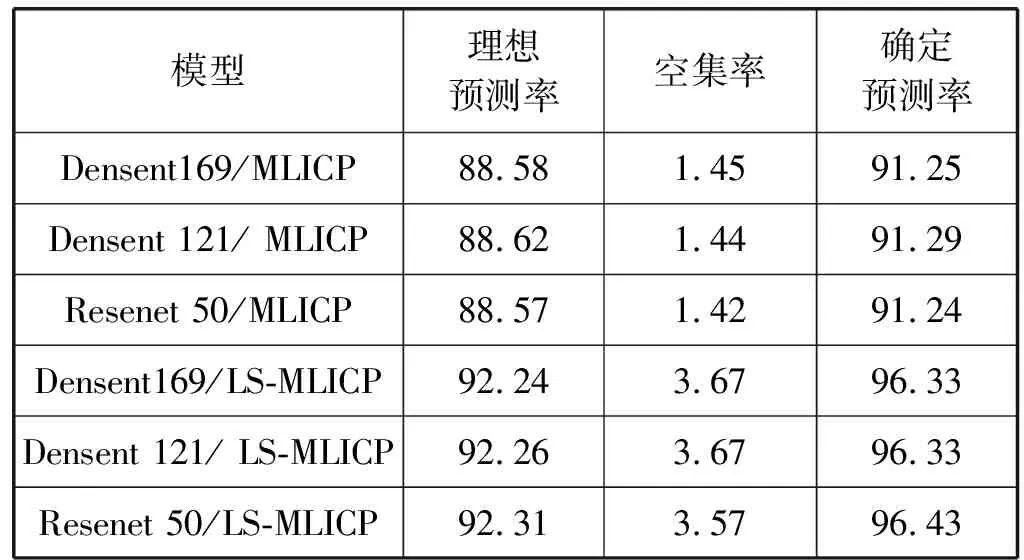
表1 MLICP-CNN预测效率比较(95%置信度) %

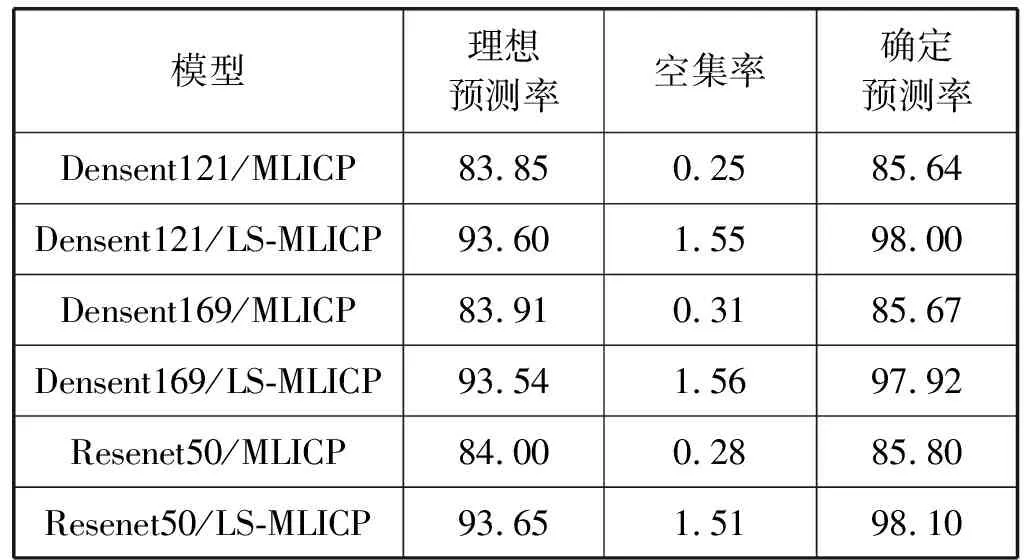
表2 MLICP-CNN预测效率比较(98%置信度) %

表1和表2展示不同CNN架构各种模型的预测效率。从表1可以看出， Resenet50/ LS-MLICP参数配置下模型的综合性能最好，即采用Resenet50的CNN架构和LS-MLICP的奇异值映射函数下，模型的确定预测率和理想预测率的数值最高。进一步地，我们展示因素对预测效率的影响，以方差形式进行计算。以理想预测率为例，在相同的MILCP奇异值函数下，三种CNN架构造成的波动约为4.67×10-4，而相同LS-MILCP奇异值函数下，三种CNN架构造成的波动约为4.67×10-4。另外，在相同Densent169架构下，不同奇异函数造成的波动是1.674。在相同Densent121架构下，不同奇异函数造成的波动约为1.656。在相同Resenet 50架构下，不同奇异函数造成的波动约为1.748。以上说明，CNN架构对预测效率的影响程度远远小于奇异函数设计的不同。从表2可见，其结果和趋势与表1一致。

4 结 语

本文提出一种基于CNN与归纳一致性预测器(ICP)的多标记胸片置信诊断模型MLICP-CNN。该模型是一种能独立为每一个测试数据提供有效置信度预测的学习框架，其核心技术包括归纳推理和算法随机性测试，前者用于构建学习规则D，后者来获取检验样本序列每个样本的样本奇异值，进而在指定风险水平下产生多标记预测集。

在对Chest X-ray14胸片数据集的实验结果表明， MLICP-CNN模型在临床常用的95%置信度下，模型准确率为95%，体现了置信度评估的恰好可校准性。而且采用Resenet50的CNN架构和LS-MLICP的奇异值映射函数下，模型性能最好，其确定预测率为96.43%，理想预测率为92.31%。另外，CNN架构对预测效率的影响程度远远小于奇异函数设计的不同。

本文提出的模型能够解决个性化胸片诊断的高风险评估问题，使胸片诊断更加符合医疗的需求。未来的工作包括设计更多的奇异函数、探讨进一步提高模型效率的途径以及多标记问题的其他转化方法等。