基于稀疏表示和决策融合的图像分类方法
储岳中 李家浩 张学锋 纪 滨
(安徽工业大学计算机科学与技术学院 安徽 马鞍山 243002)
0 引 言
图像分类是当前计算机视觉、深度学习和人工智能等领域的研究热点。在图像分类这一研究课题下,文献[1]对该课题近些年的发展作出总结和展望,表示多特征融合这一策略对图像分类具有非常关键的研究意义,并且在选取特征与分类器这两个关键环节的处理对最终分类效果具有深远影响,往往多特征伴随着高维度数据且伴有各类噪声影响。压缩感知技术研究的热潮下,文献[2]提出稀疏表示下的人脸识别算法,通过训练样本来计算稀疏系数与字典,然后计算残差来获得最终分类的方法,取得很高的识别率。从字典学习的角度,文献[3]提出KSVD字典学习算法,通过k次迭代,每步计算SVD分解来更新字典原子与对应系数的方法,从而获得优化的解。文献[4]在其基础上改进并提出LC-KSVD算法,通过整合构建字典与优化线性分类器到重建的目标函数中,联合获取更优化的学习字典。近些年各类基于稀疏表示的改进方法被不断提出[5],但很少有多特征融合结合稀疏表示分类器展开研究的方法,由于单一特征对图像描述不足以及分类器性能存在的差异性,导致传统的分类方法在最后的分类效果上性能的局限性较大。多特征融合的分类算法近些年不断被提出,文献[6]根据特征不确定性提出一种新度量方式去对各类特征贡献进行调整,以保证融合算法的鲁棒性和稳定性。由于多特征融合所带来的特征维度过高以及特征表现不明确等问题,文献[7]提出多内核低秩字典学习方法(MKLDPL),能够有效通过对多特征进行多核字典学习。围绕图像分类这一主题,结合多特征融合思想,稀疏表示分类器可有效减少遮挡、旋转等因素对图像识别的影响,为图像分类提供了新的手段。
针对特征提取与分类器融合等问题,本文通过自适应的融合多特征所生成的稀疏表示分类器结果,并结合整体特征与局部轮廓特征在不同分类情景下的权重比等因素,通过对多特征分类器融合决策的方法充分发挥各特征在不同分类情景下的最大优势。实验表明,多特征稀疏表示分类器融合的分类方法,较单一特征分类器的效果有显著提升,构成了一种容错性高且鲁棒性强的多特征融合图像分类系统。
1 多特征提取
1.1 全局Gist特征提取
Gist最早是由文献[8]提出,而后在2006年文献[9]提出对图像使用多尺度多方向Gabor滤波器组进行处理的Gist特征提取方法,全局Gist特征提取一般采用4个尺度、8个方向的Gabor滤波器组进行全局特征的提取。对图像进行全局Gist特征提取的具体步骤如下:
(1) 将一张大小为m×n的灰度图片划分成ma×nb个分块图片,每张分块图片的大小为m*×n*,其中m*=m/ma,n*=n/nb。
(2) 使用Jc个通道的Gabor滤波器对每块局部图像进行卷积滤波,其中Jc个数等于滤波器尺度与方向数的乘积,滤波产生的各网格各通道后级联的结果为该图像块Gist特征,公式为:
(1)
式中:Gi的维数是Jc×m*×n*,由于默认尺度为4个尺度、8个方向,所以i=[1,2,…,32]。
(3) 将Gi(x,y)经滤波器处理后的特征值取均值,再将均值化以后的特征值组合起来,融合形成最终整张图片的Gist特征,即:
(2)
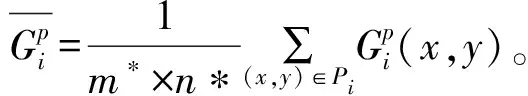
本文在提取研究目标图像的Gist特征时,选择4×4的网格对整张图像进行划分,即最后得到的特征维数为32×16=512维。该特征很好地保留了整张照片的全局特征信息,
由于PCA 降维方法能够对数据进行压缩,消除冗余和数据噪声,尽可能保留原始数据中的重要特征信息,最大限度地减少降维带来的损失,所以采用PCA方法对Gist特征进行降维,以达到最优化效果,缩短分类时间。
1.2 Dense-SIFT特征提取
SIFT特征描述子是由Lowe[10]于2004年提出的一种对图像缩放、旋转和仿射变换具有不变形的特征描述子,根据Koendetink[11]建立的高斯核为唯一线性核理论,提取该特征首先通过对样本二维平面空间与DoG(Difference of Gaussian)中同时检测局部极值点,DoG算子如下:
D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ))×I(x,y)=
L(x,y,kσ)-L(x,y,σ)
(3)
式中:L代表图像的尺度空间,I(x,y)代表图像(x,y)位置的像素值,G(x,y,σ)为二维高斯核函数。Lowe在原论文中建议SIFT描述子使用在特征点尺度空间内4×4的窗口中计算的8个方向的梯度信息,共4×4×8=128维向量表示,最终各训练样本生成的特征向量为m×n,其中n为图像生成的特征向量个数。
Dense SIFT特征提取是由SIFT特征提取演变而来,相较SIFT特征描述子更加均匀平衡地分布在图像的各区域。由于其特征点检测这一部分不同于SIFT特征,通过对图像进行等大小的网格划分,设定一个固定大小n×n的正方形滑动窗口,如图1所示。按照Bin size进行左右上下滑动,截取生成采样空间块,生成8个方向上的梯度直方图,然后将每个采样空间块n×n的8位维度连接起来,形成Dense-Sift描述符。

图1 Dense-SIFT滑动窗口的特征采样
1.3 方向梯度直方图
方向梯度直方图(histofram orented gradient,HOG)是由Dalal[12]在2005年提出,具有很强的图像特征描述能力,对图像几何与光照的形变都具有较强的鲁棒性。HOG特征对边缘尤为敏感,在作为融合决策中能够充分发挥局部特征对分类所产生的重要影响,所以本文选取该特征作为多特征稀疏表示分类之一。HOG算法首先将像素大小为m×n的测试图像样本划分成大小为mi×ni的细胞,并将2×2个细胞组成一个块,水平方向和垂直方向分别按照一个细胞大小的步长为滑动窗口,计算各像素点的梯度大小和方向,每个细胞内按照像素的梯度方向形成的方向直方图,方向直方图的组数b,最后获得36×(m/mi-1)×(n/ni-1)个特征向量,图2中对样本图像的边缘信息进行描述。

图2 图像灰度图的HOG特征对应轮廓图
由图2可发现,HOG特征对样本几何变化性具有较强的鲁棒性,对样本局部轮廓特征具有良好表现,类似于其他特征提取生成特征向量的高维数问题,本文同样对生成的HOG特征向量进行降维处理,最大程度保存其特征表达的完整性。
2 多稀疏表示分类器构成
2.1 稀疏表示分类(SRC)方法
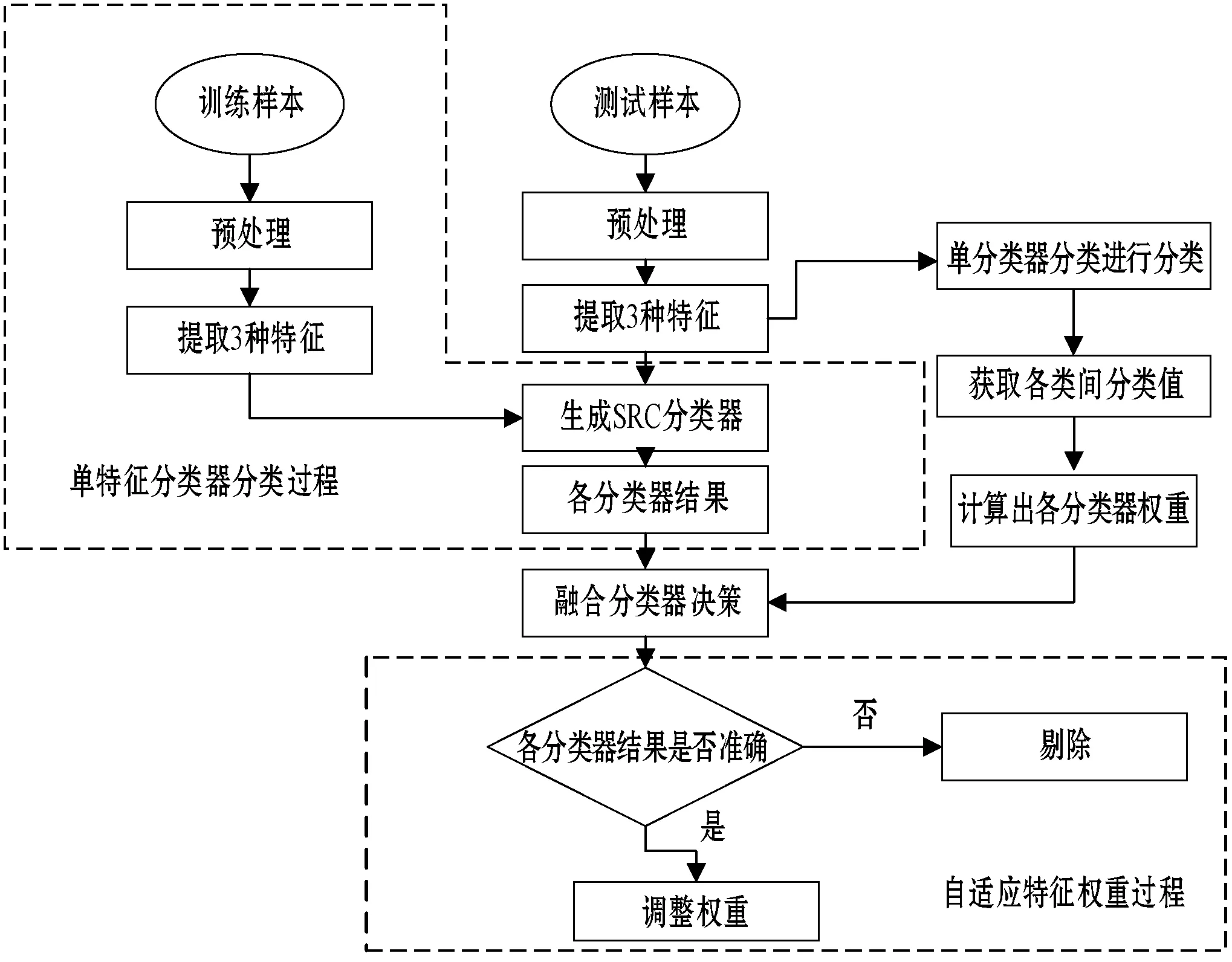
设有M类训练样本,Ki=[ki1,ki2,…,kini]∈Rm×ni表示第i类训练样本所构成的样本集合,kij∈Rm表示第i类第j个训练样本图像向量,其中m为训练样本图像向量的维数,ni为第i类训练样本的个数。D=[D1,D1,…,DM]∈Rm×n表示整个训练样本图像的训练样本矩阵,n为训练样本图像的总数,令矩阵D为字典,给定测试样本y可由字典D表示,即y=Dx。其中,y可由所在类组成的图像向量线性表示,即y=ki1xi1+ki2xi2+…+kinxin,x为该测试样本对应字典D的稀疏表示编码,若训练样本数量足够多,y对应字典D所生成的稀疏表示编码x稀疏,由于m< (4) 式(4)为NP问题,由文献[13]提出的可将l0范数问题转化为求解l1范数最优化问题,由于数据量过多且存在不同程度噪音等影响,加入误差约束项: (5) class(y)=argminri(y) (6) 最终基于式(6)的分类规则对测试图像y进行分类。 通过对不同特征生成的分类器进行准确率验证,分别构造多个稀疏分类器,根据不同的分类器在所有特征情况下的准确率进行权重分配,通过迭代更新不同特征分类器的权重占比,最后通过最终决策分类器输出结果。 文献[14]提出关于多分类器融合判别系统,多分类器融合决策的关键问题是特征多样性以及决策融合方法合理性,不同多分类器融合决策系统对不同的需求模型有不同的性能表现。基于此概念,结合在图像分类这一多因素影响的复杂课题下,具备单一特征信息的分类模型很难具有很良好表现,例如全局Gist特征虽然能够在全局上很好把握整体轮廓图像特征完整性,但对于局部特征具有较高决策权重比的分类任务下,仅单靠全局Gist特征来对图像进行决策分类,效果并不理想。Hog特征着重提取图像轮廓与方向梯度特征,对表现图像局部特征有着显著的效果,但整体旋转变化鲁棒性并不强,在多分类器融合决策下,能够很好应对复杂情况下的图像分类问题。 本文通过引入自适应调节各分类器在最终决策结果的影响因子权重比,通过各特征稀疏表示分类器对不同样本存在不同程度的准确性;通过奖惩因子∂合理地对各分类器进行自适应权重调节,∂的参数大小选取对分类准确率也有一定影响;通过不断迭代与自适应更新参数获得最优多分类器融合决策模型。整个分类决策建模过程如图3所示。 图3 基于多特征稀疏表示分类器的图像识别算法流程图 具体过程如下: 步骤1首先根据第2节提出的三种特征提取的方法分别对整个训练样本进行特征提取,获得三组训练样本特征矩阵: Dk=[D1,D2,…,DM]∈Rd×n (7) 式中:d为该特征维数,M为样本总类别数,k为第k类特征,Dik为第i类样本的第k类特征向量。 (8) 步骤3构造分配各稀疏表示分类器初始权重,按照首次各子分类器输出的分离程度P,获得初始化特征权重系数为: (9) Wi代表第i类稀疏表示分类所分配的初始化权重比。 步骤4融合各加权稀疏表示分类器的分类结果,确定图像所属类别: (10) (11) 仿真环境为Windows 7操作系统,Intel Core i7 CPU,内存16 GB,编程环境为MATLAB 2016a。 为了验证本文方法相较单个特征提取之后的分类效果有较高提升,基于cifar-10图像数据数据集进行验证实验,本实验所有数据来自CIFAR-10数据集。该数据集共有60 000幅样本图样,样本大小均为32×32,像素分为10类,每类6 000幅图。这里训练样本集分5批,每批样本集包括带标签的样本10 000幅,另剩下10 000幅作为一批用于测试样本集。由于该数据集中样本均为彩色图片,本文进行所有实验之前,先进行预处理,均对图片进行了灰度化与归一化处理,转换为灰度图进行特征提取,如图4所示。 图4 Cifar-10数据库部分预处理后的图像 验证根据Gist、Dense-SIFT和HOG三种特征,分别对其结合各自生成的稀疏表示器进行单一决策与联合决策的图像分类实验。通过对比单一特征的稀疏表示分类器在不同图集的正确率,来显示不同图像分类任务下各特征对分类结果有不同的表现。 表1显示了不同特征生成的稀疏表示分类器在各测试样本图集上的识别正确率。由表1可以明显发现不同特征所生成的稀疏表示分类在不同子集上的识别率有着明显的差异,由此可看出,仅对图像进行单一的特征提取并不具备良好的分类能力。其中Gist特征稀疏表示分类相比HOG特征稀疏表示分类,在分类准确率上有3%~5%的提升,而Dense-SIFT特征描述子所生成的稀疏表示分类从识别率上明显优于其他两种,Dense-SIFT特征更加注重对全局特征信息的均衡表示。 表1 单特征稀疏表示分类器在不同训练集识别率 % 由第2.2节提出的融合决策方法,对各特征进行自适应权重融合后,不同特征在不同训练集合上图像识别率以及权重比如表2所示。 表2 本文方法在不同训练集下的各特征权重与识别率 由表2可看出,Gist特征与Dense-SIFT所占比重较大,通过结合三类特征各自的稀疏表示分类器的分类结果联合决策,图像识别的准确率在五个不同图集上有着不同程度的提升,通过调整奖惩因子∂的参数权重比,来观测其对准确率的影响。如图5所示。 图5 奖惩因子变化所对应分类准确率 由图5可以看出,奖惩因子∂的数值变化对准确率也有着很大影响,通过实验可以证明在验证图集的分类任务下,以因子∂=5可让整个联合决策分类器效果达到最佳。 为了验证本文算法相较单一决策分类器的准确率有明显差距,选取SVM、GSRC[15]、KNN、与本文方法在不同图集上进行验证比较,结果如表3所示。 表3 本文方法与其他分类器方法在不同图集准确率 % 由表3可看出,仅提取单特征产生的稀疏表示分类器进行分类决策的实验与基于不同分类器在不同子集的实验作对比,传统KNN分类器分类准确率仅为0.23至0.25之间,本文方法相对SVM与GSRC分类器的分类效果与分类精度有着显著的提升。从以上基于单特征下与不同分类器下的2组对比实验,可以发现,通过使用多稀疏表示分类的融合决策模型进行图像分类,相比单一特征的图像分类方法表现出了更好的识别效果。 本文提出了一种多稀疏表示分类器融合的图像分类方法,通过构造3种特征所生成的稀疏表示分类器的融合决策模型,并自适应调整每个稀疏表示分类之间的权重,最后通过线性加权的方式对图像进行分类。实验数据表明,本文方法较好地克服了单特征存在的特征局限性以及不同特征对不同样本分类情况下的影响权重比不同的问题。在接下来的研究当中,主要还会对选择组成多稀疏表示分类器的特征这一方向从深度学习与字典学习等方向寻找图像分类更佳的解决方案。2.2 多分类器权重融合

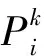

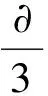
3 实验及结果分析
3.1 实验环境

3.2 单个特征下的图像分类对比实验
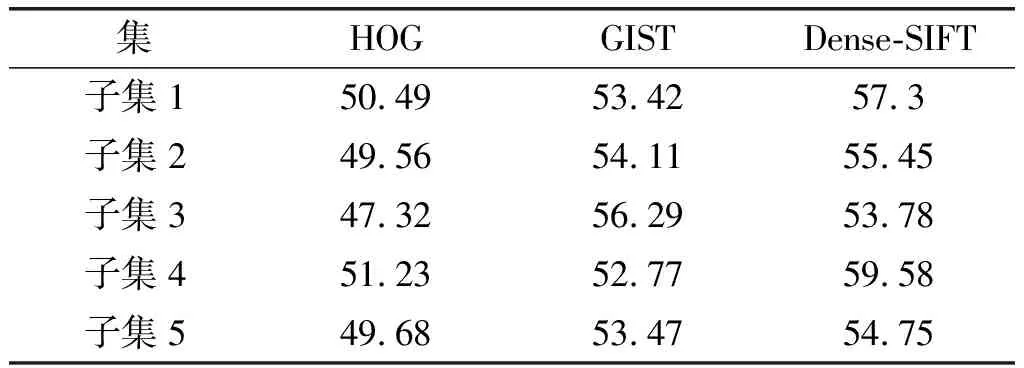


3.3 基于不同分类器的分类对比实验

4 结 语

