一类矩阵不等式的进一步加强

缪佩佳，倪若兰，蔡 璐

(阿坝师范学院数学与计算机科学学院， 四川 汶川 623000)

用Mn表示所有n×n 复矩阵的集合， 对于Hermite 矩阵A，B∈Mn， 偏序A≥B 表示矩阵A-B 半正定. 设v为实数， 且0 ≤v ≤1，矩阵A 和B 的v-加权几何均值的定义如下:

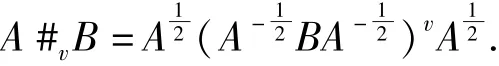
设A，B∈Mn正定， Kittaneh 和Manasrah 在文献[12]中证明了: 若0 ≤v ≤1，则

其中r0＝min v，1 -v{ }，s0＝max v，1 -v{ }.

随后， 邹黎敏在文献[16]中将不等式(1)改进为: 若0 ≤v ≤1，则

在本文中，将利用文献[12] 和文献[16]中的方法， 进一步改进不等式(2).

1 关于几个标量不等式的改进

在文献[10]中， Bhatia 证明了， 若0 ≤v ≤1， α v( )＝4(v-v2)， 则

首先改进不等式(3)、(4).

定理1 设a，b≥0，0 ≤v ≤1， 则

证明 不等式(5)等价于

即证.

因此， 不等式(5)是不等式(3)的进一步加强.

下面， 将不等式(4)进一步改进为:

定理2 设a，b ＞0，d ＝max a，b( )，0 ≤v ≤1， 则

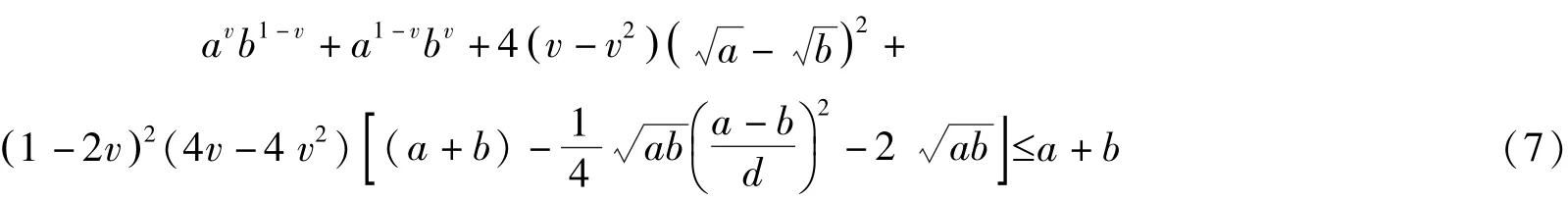
证明 由于a，b ＞0， 因此可令a ＝ex，b ＝ey(x，y∈R). 设

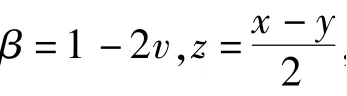
下面首先证明:

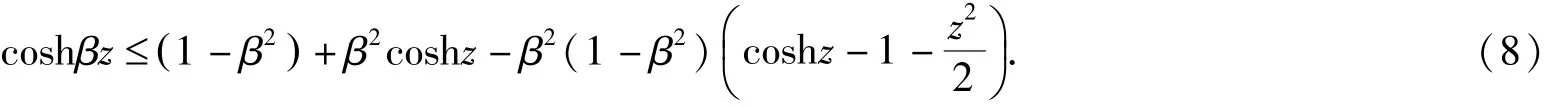
由双曲函数cosh x 的泰勒级数展开式可知

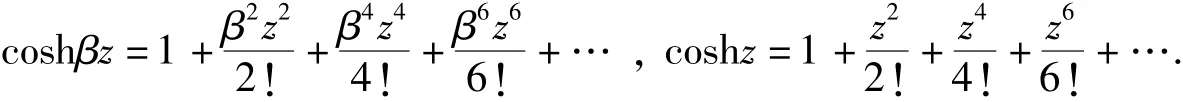
因此(8)式等价于

即

于是， (9)式成立， 因而(8)式成立.

在(8)式中， 令a ＝ex，b ＝ey(x，y∈R)， 则可得

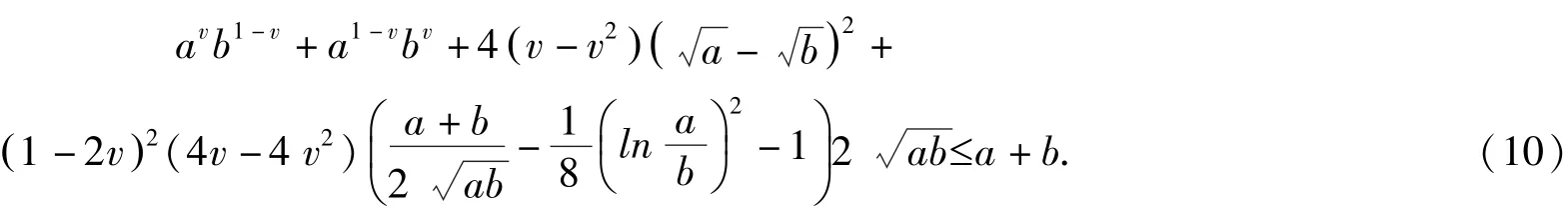
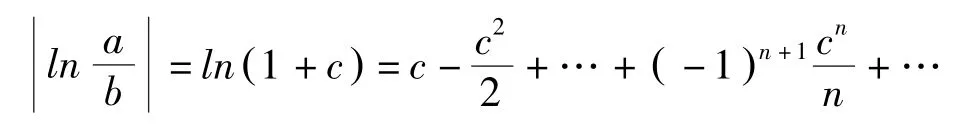
则

由(10)式和(11)式即可得， 不等式(7)成立.证毕.

并且由于1 -2v( )2≥0，4v-4 v2≥0， 因此， (7)式是(4)式的进一步加强.

2 主要定理及其证明

在这节中，将改进不等式(2).

定理3 设A，B∈Mn是正定矩阵， 若0≤v≤1， 则

证明 对任意的正定矩阵T，由谱分解定理可知， 存在酉矩阵U∈Mn，使得T ＝UD U∗，

其中，

对任意的正数a，由不等式(5)有

因此

其中I 为单位矩阵. 将(13)式的左右两边分别乘以U，U∗，可得

在不等式(14)中，令

因为A、B 是正定的， 即可得不等式(12).

定理4 设A，B∈Mn是正定矩阵， 假设B-A 正定， 若0 ≤v ≤1， 则

其中D ＝diag ( λ1…λn)，λj＞0，1 ≤j ≤n.

令式(7)中令a ＝1，对任意的正数b≥0， 则有

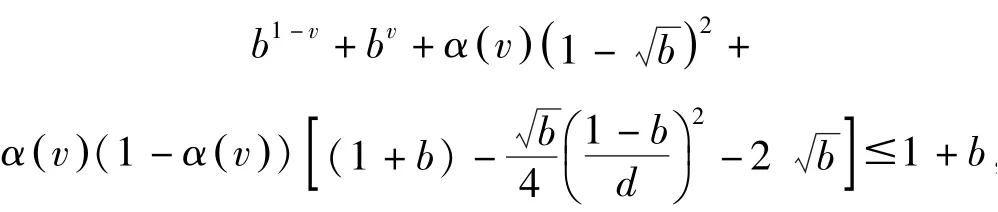
其中d ＝max(1， b). 因此

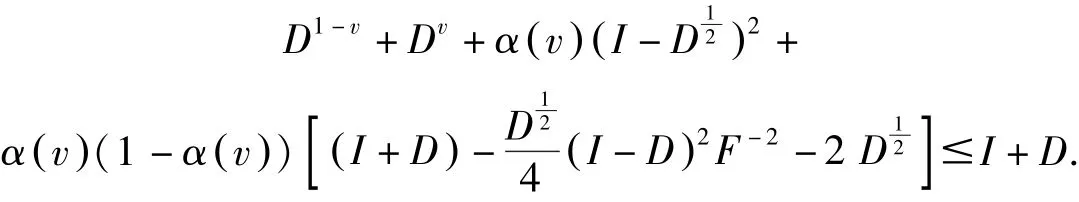
其中

在上式的左右两边分别乘以U，U∗，可得

在(16)式中，不妨设F ＝D， 则T-I 正定， 由于

其中α v( )＝4(v-v2).

证明 对任意的正定矩阵T， 由谱分解定理可知， 存在酉矩阵U∈Mn， 使得T ＝UD U∗，

3 结论

该文首先对不等式(3)以及不等式(4)这两个标量不等式进行了进一步改进， 再利用谱分解定理， 对关于矩阵A 和B 的v-加权几何均值的上下界进行了相应的改进， 得到了不等式(12)和(15)， 从而进一步加强了Kittaneh 和Manasrah、邹黎敏等学者的文献中的结果.

致谢 作者衷心感谢阿坝师范学院杨仕椿教授的悉心指导和热情帮助!