某类解析函数的Fekete-Szegö 不等式
牛潇萌
(赤峰学院数学与统计学院, 内蒙古 赤峰 024000)
1 引言

的函数类的全体.用S∗表示星象函数类,用C 表示近于凸函数类,S∗和C 都是S 的子类.
定义1.1[1]设函数f(z)与g(z)在U 内解析,如果存在U 内满足的解析函数ω(z),满足g(z)=f(ω(z)),称为g(z)从属于f(z),记为g(z)pf(z).
设-1 ≤B <A ≤1,用P(A,B)表示在U 内解析并且满足条件的所有函数的全体.显然P(1,-1) =P 为熟知的正实部函数类.
1933 年, Fekete 和Szegö 在文献[2] 中提出了函数族S 上的系数泛函的准确估计, 近些年来,许多作者研究了不同解析函数类上的Fekete-Szegö 问题.如文献[3-13] 分别引入了一些特殊解析函数类, 并讨论了其Fekete-Szegö 不等式问题.
刘名生在文献[14]中给出了如下函数类.
定义1.2[14]设f(z)∈S,α >0,λ≥0,-1 ≤B <A ≤1,若存在g(z)∈S∗,使得

则称f(z)∈B(λ,α,A,B,g(z)). 子类B(1,α,1,-1,z)是Bazilevic 函数类的子类.
定义1.3[15]设f(z)∈S,α >0,λ≥0,σ <1,若

则称f(z)∈Ρ(λ,α,σ). 显然B(λ,α,1 -2σ,-1,z) =Ρ(λ,α,σ).
刘名生在文献[14]中研究函数类B(λ,α,A,B,g(z)),得到其从属关系,包含关系,偏差定理等.但是关于函数类B(λ,α,A,B,g(z))的Fekete-Szegö 不等式还尚未研究过. 本文将给出B(λ,α,A,B,g(z))的Fekete-Szegö 不等式,进一步给出Ρ(λ,α,σ)的Fekete-Szegö 不等式.
2 主要结论
为了证明B(λ,α,A,B,g(z))的Fekete-Szegö 不等式,需要如下引理.
引理2.1[16]设ω(z) =c1z +c2z2+…在U 内解析,且,则有.
引理2.2[17]设p(z) =1 +p1z +p2z2+…∈P,则有

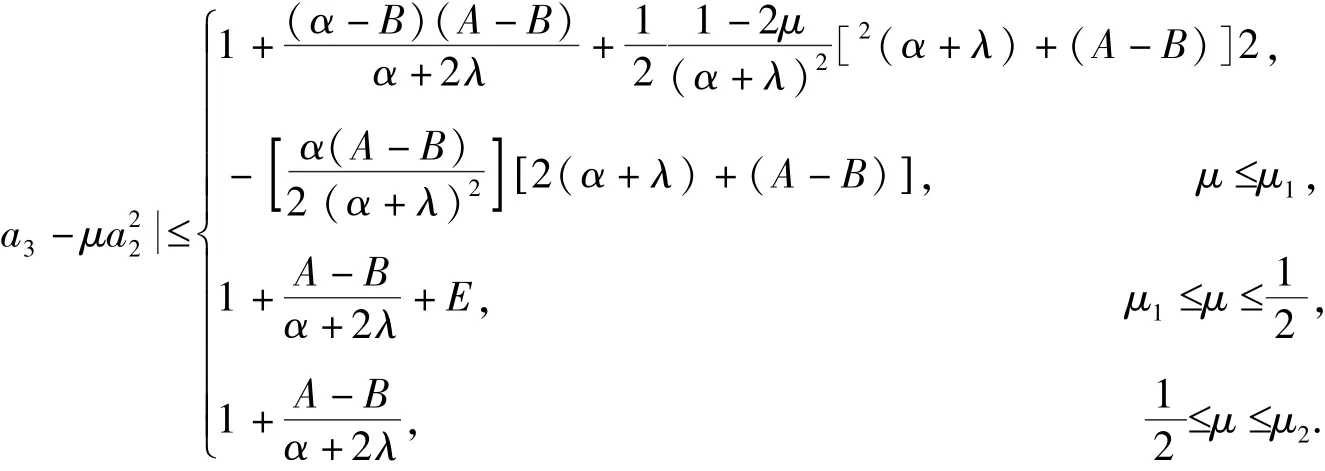
其中,

证明 设f(z)∈B(λ,α,A,B,g(z)),则存在,使得


整理得

由Taylor 展开式并比较(2)式两边zα+1z 和zα+1z2两项的系数可得

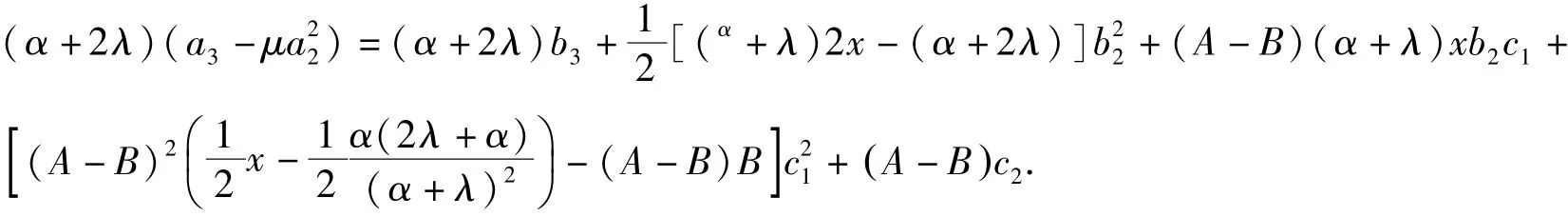
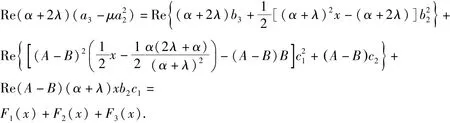

令p1=2leiβ,0 ≤l ≤1,则由引理2.2 可知

而

由引理2.1 可知

令c1=reiθ,0 ≤r ≤1,则

因为b2=p1=2leiβ,c1=reiθ,所以有

所以

其中
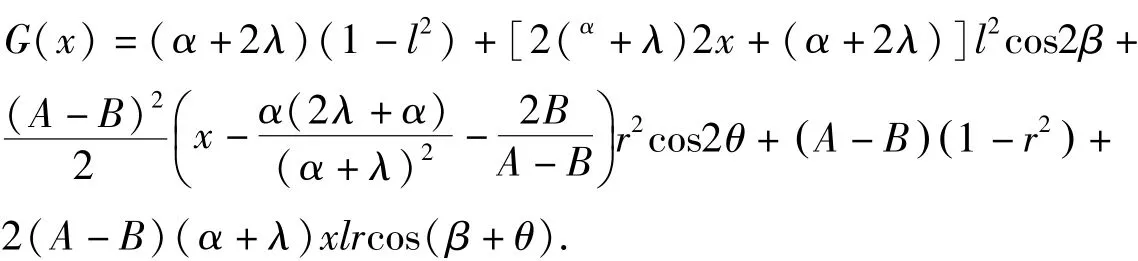

最后一个不等式成立的条件如下:

又因为x≥0,经简单计算可得


从而

由(1)的证明可知

从而

当μ ≤μ1时,不存在极值函数.

经简单计算可知

其中

令
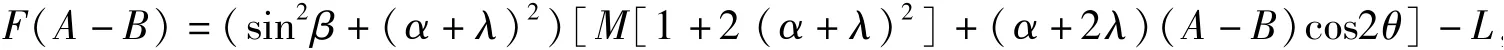
易知,F(A-B)是(A-B)的一次函数.

因为F(A-B)是(A-B)的一次函数,所以当0 ≤(A-B)≤2 时,F(A-B)≥0,从而G(x1)≤α +2λ +A -B.对于0 ≤t ≤1,有

当b2=0,b3=1,c1=0,c2=1 时等号成立.
由于B(λ,α,1 -2σ,-1,z) =Ρ(λ,α,σ), 在定理2.1 中取A =1 -2σ,B =-1,g(z) =z,可得如下推论.

其中,


