有容量限制的仓库选址及调运问题研究

范昌胜，徐锦华，陈新庄，李 斌

(1.陕西工商职业学院工程与建筑学院，陕西 西安 710119；2.西北工业大学理学院应用数学系，陕西 西安 710072)

当前的物流行业通过仓储、运输、配送等形式进行全面综合管理，使得在物流过程中缩短了时间，降低了成本.众多大型物流配送企业都会共同遇到类似的仓库选址及调运问题.通常采用将物流网络中的仓库合理分散设置的方案，制定恰当的仓库选址及车辆出行线路，最大程度地为分散的用户提供一定的服务，又能降低整个系统运行的总费用[1-2].

对仓库选址问题的研究，国内外的学者都寄予很高的重视，对此问题的解决，有精确算法和近似算法两种.主要包括分支定界法，拉格朗日松弛法，禁忌搜索法，模拟退火法、遗传算法[2-3]及一些混合算法.在国外，对无容量约束的仓库选址问题，文献[4]给出了禁忌搜索算法；对有容量约束的仓库选址问题，文献[5]对此问题的解决方法从精确算法和近似算法进行了总结，文献[6]给出了增加或减少仓库的启发式算法.在国内，文献[7]用单亲进化遗传算法解决有仓库容量限制的选址问题，这要求一个需求点仅由一个配送中心(仓库)供应，上述文献所研究的都是只考虑仓库和需求点之间的供应关系. 还有许多文献对上述选址问题进行了扩展，考虑工厂，仓库，需求点三层之间的供应关系.文献[8]研究了只有一个工厂的情形，并用混合遗传算法求得其近似最优解.文献[9]考虑了多工厂的情形，用启发式算法进行求解，不过仓库的固定费用没有反映在解值上.文献[10-12]通过把三层关系转化成两层关系来求解，即在优化两层关系的前提下，按随机要求从工厂向仓库供应货物.并用拉格朗日松弛法和遗传算法求得其最优解.

在上述问题研究的基础上，对有仓库容量限制，多工厂的三层供应关系的仓库选址问题进行了研究，给出了一种精确算法.这种算法在求出工厂到仓库、仓库到销售点最短路径的前提下，在满足仓库容量限制的基础上，找出可降费的闭合回路进行调整，最后再通过减少仓库个数确定最优仓库个数和运输路线.这种算法用计算机语言很容易编程实现，具有计算速度高，存储空间少等优点.

1 问题描述及其数学模型

在现实生活中，产品的流通与否直接影响着企业的经济效益，为了方便产品的流通，工厂经常需要建立或租赁仓库来存储货物，以达到使整个物流环节的费用支出最小，对于这种活动，可以描述为以下数学问题.

问题描述:在有N 个节点的无向连通网络中，节点Ai表示工厂(i ＝1，2，...m)，Bj表示仓库(j ＝m ＋1，m ＋2，…m ＋s)，Ck表示销售点(k ＝m ＋s ＋1，m ＋s ＋2，…m ＋s ＋n)，并且满足m ＋s ＋n ≤N；已知第Ai个工厂可提供货物量为Pi，第Bj个仓库的容量为Rj、租赁费为Fj， 第Ck个销售点需求货物量为Qk，并且满足又已知网络中任意相邻节点i 和j 间的单位运费为Sij＝Sji(1 ≤i，j ≤N)[13].

研究:如何选择工厂到仓库的运输线路，仓库到销售点的运输线路，才可使所有货物从工厂运送到仓库再到销售点的总成本最低(总成本包括仓库租赁费和货物运输费用)?

问题分析:这个问题具有很广泛的现实意义，根据问题描述，我们解决的思路是把N 个节点分成三类点，工厂、仓库和销售点，在已知任意相邻两点i 和j 间的单位运费Sij(1 ≤i，j ≤N)的前提下，用Floyd 算法求得从工厂到仓库最短路径cij，从仓库到销售点的最短路径cjk.在此转化的基础上，可得到以下数学模型:

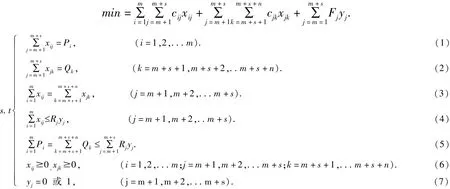
其中:xij＞0 表示第i 个工厂向第j 个仓库运输货物，且运量为xij，xij＝0 表示第i 个工厂向第j 个仓库无运量；同理，xjk＞0 表示第j 个仓库向第k 个销售点运输货物，且运量为xjk，xjk＝0 表示第j 个仓库向第k 个销售点无运量.

目标函数是最小化所有费用，其中前两项为运输费用，最后一项为仓库租赁费用.(1)表示从工厂发出的货物总和应等于它所提供的货物；(2)表示销售点的需求量应得到满足；(3)表示由工厂发往每个仓库的货物量等于该仓库满足其销售点的货物量；(4)表示如果第j 个仓库被选中，则它接收的货物总量不得超过它的容量；(5)表示工厂和销售点的货物总和相等，并且不超过所有被选中仓库的总货物量；(6)和(7)是变量约束[14].

2 算法步骤

由于选址问题是NP 困难问题，对原问题的解决，我们分为两个阶段[15].

2.1 第一阶段

根据Floyd 算法把题中Sij(1 ≤i，j ≤N) 转化成cij，cjk(i ＝1，2，..m； j ＝m ＋1，m ＋2，…m ＋s； k ＝m ＋s ＋1，…m ＋s ＋n)，具体算法步骤如下:

①输入 Sij(i，j ＝1，2，...N)；dij⇐Sij， pij⇐j. ( i，j ＝1，2，...N) k⇐1.

(注:当节点i 与节点j 不相邻时， Sij＝∞； 当 i ＝j 时， Sij＝0)

②若dik＋dkj＝μ ＜dij， 则 dij⇐μ， pij⇐pik；

否则(μ≥dij) dij与pij都不变( i，j ＝1，2，...N).

③若k ＜N， 则k⇐k ＋1 ，转到②； 否则 (k ＝N) 转到④.

④cij⇐dij， cjk⇐djk，

( i ＝1， 2，...，m； j ＝m ＋1，..m ＋s； k ＝m ＋s ＋1，...，m ＋s ＋n).

2.2 第二阶段

1)先根据最小元素法求得工厂到仓库和仓库到销售点的初始租赁方案，其中R'j为仓库的待分配量，bj为仓库的剩余容量，具体算法步骤如下:

①输入Pi， Rj，Qk， S⇐充分大的数， bj⇐Rj， P'i⇐Pi， bk⇐Qk，

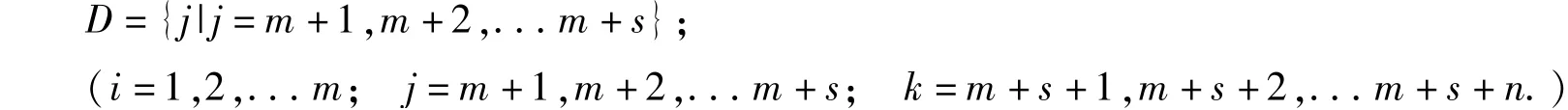
②求min{cij｜i ＝1， 2，...m； j ＝m ＋1，m ＋2，...m ＋s}Δ＝ μ，

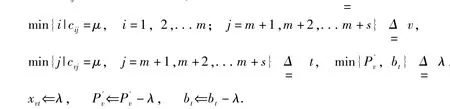
否则(bt＝0)，x⇐0，(i ＝1，2，...m；i≠v).

⑤求min{cjk｜j ＝m ＋1，m ＋2，...m ＋s； k ＝m ＋s ＋1，...m ＋s ＋n} Δ μ

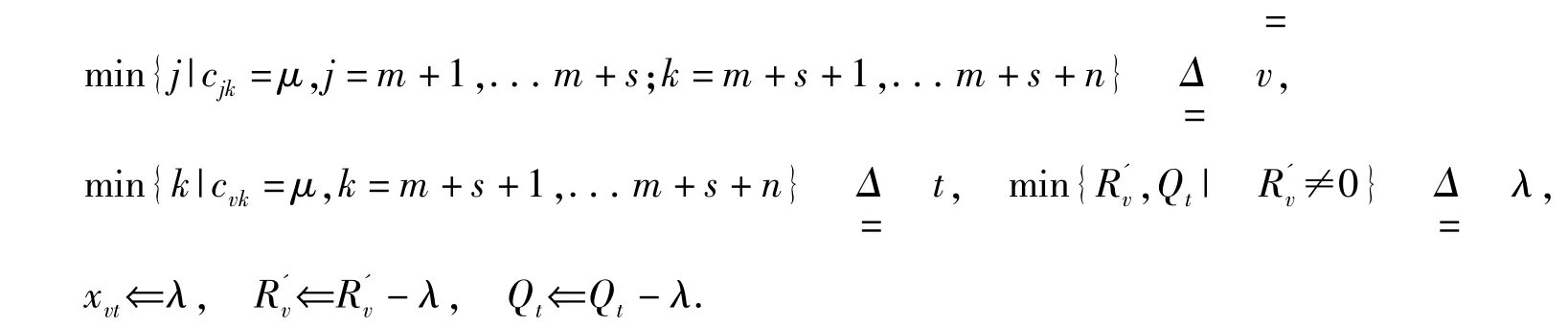
⑥若(R'v＝0)， 则 xvk⇐0， (k ＝m ＋s ＋1，m ＋s ＋2，...m ＋s ＋n；k≠t)；

否则 (Qt＝0)， 则 xjt⇐0， (j ＝m ＋1，m ＋2，...m ＋s；j≠v).

2) 对每一种租赁方案找可降费的闭合回路进行调整，在1)的基础上，直到不能再调整为止，得最优解，具体步骤见⑧-⑭.

⑧ i ＝1， k ＝m ＋s ＋1.

⑩若 k ＜m ＋s ＋n， k⇐k ＋1， 转⑨； 否则 ( k ＝m ＋s ＋n)，转⑪.

⑪若 i ＜m， i⇐i ＋1， 转⑨； 否则 (i ＝m)， 转⑫.

⑫若j ＜m ＋s， j⇐j ＋1， 转⑧； 否则 (j ＝m ＋s)， 转⑭.

⑬求min {xij，xjk，bt｜xij＞0， xjk＞0， bt＞0，

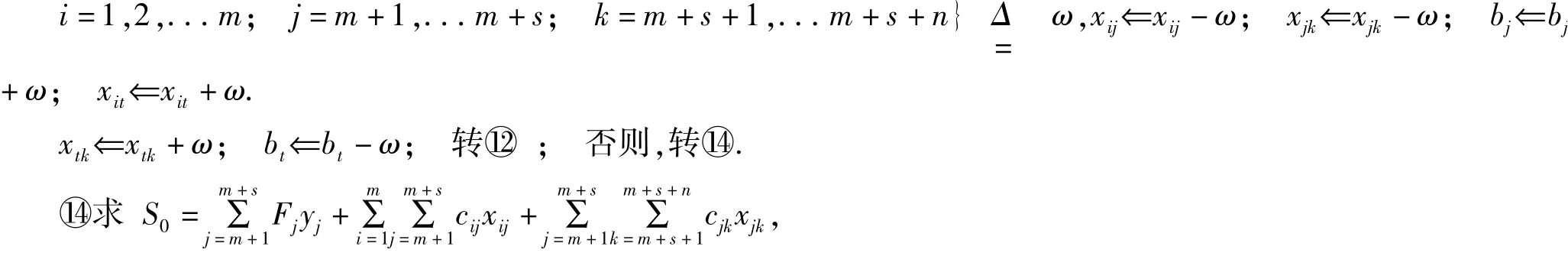
若S0＜S，则S⇐S0，转⑮；否则，转⑲.

3) 在2)得到解的基础上，逐个判断此时仓库Bj(j ＝m ＋1，m ＋2，…m ＋s)的通过量是否小于其余仓库的剩余容量总和，若是，逐个去掉仓库按步骤②-⑭，求每一种情况下的最优解，然后再判断此时的解是否小于原来的解，若是，有现在的解覆盖原来的解，再在剩下的仓库进行判断，直到不满足容量限制或不能在降费为止，得到的解，就是最后的最优解.其中集合D 表示租赁仓库的位置和个数，具体步骤如下:

⑮ j1⇐m ＋1， D ＝{ j｜ yj＝1， j ＝m ＋1，m ＋2，...m ＋s}.

⑯ 若 j1∈D， 转⑰， 否则(j1∉D)， 转⑱.

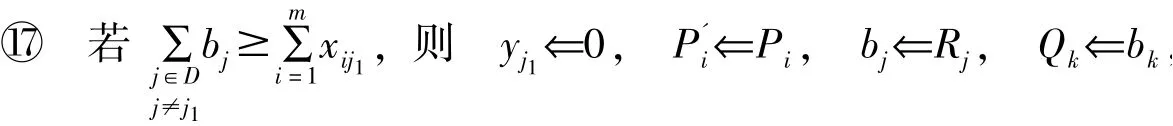
转②； 否则，转⑱.

⑱ 若 j1＜m ＋s， j1⇐j1＋1， 转⑯， 否则 s⇐s-1， 转⑮.

⑲ 输出S0， yj， xij， xjk， (i ＝1，2，...m； j ＝m ＋1，m ＋2，...m ＋s； k ＝m ＋s ＋1，m ＋s ＋2，...m＋s ＋n).

3 算例演示

依据上述第三部分算法设计，编制程序，可计算任意给定的多工厂多仓库实际调运问题.根据某物流公司业务情况，列表1 所示的十个基点中，1、2 表示为工厂，3、4、5 表示为仓库，其余为用户点.

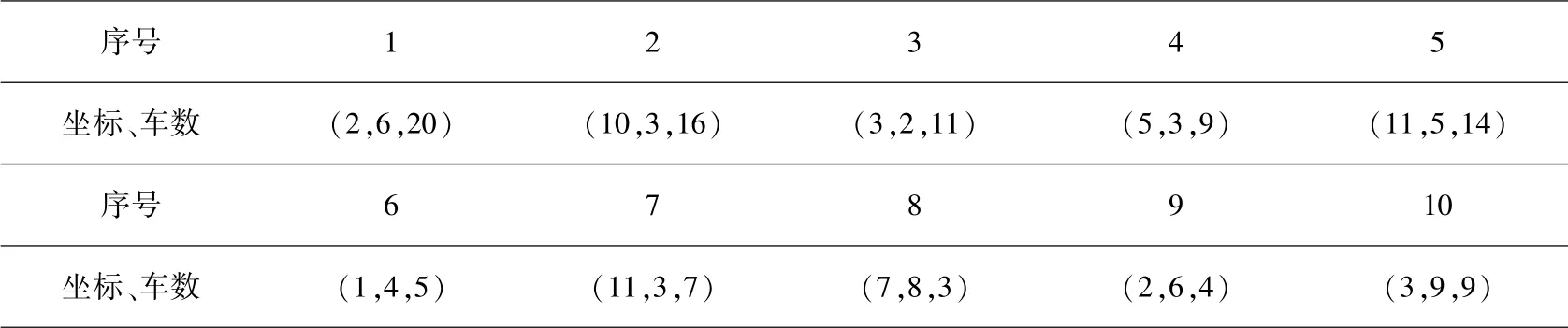
表1 算例中给定的数据信息Table 1 Data information given in theproblem

假定例中单车满载的运费核算，与实际工厂、仓库、用户之间的两点间距离成正比，其中，sij＝θdij(i，j ＝1，2，…，10)，dij表为两点间的距离，空车行驶费用表示为λsij，给出各点的坐标以及对应点车辆或货物的车数.按照第三部分的算法编制程序，取θ ＝0.5、λ ＝0.4 时，如下表2 为得到的算值:

表2 实例10 个节点的试验结果Table 2 Example test results for 10 nodes

根据上表2 中的试验结果，安排具体的车辆方案，总运费计算结果为301.029.

采用VRP Web 上实例p01 至p05 数据，扩大数据规模，进一步地检验算法适用性，编程实验，按照依次用完一个节点车辆的方法来给定初始解，取θ ＝0.5、λ ＝0.4，结果如表3 所示.

表3 实例p01 至p05 试验结果Table 3 Example p01 to p05 test results

P04 (30，30，40) 8 61 1407 1.453 739.8(100) (30，40，30) 7 272 1389 1.609 739.8 P05 (40，40，20) 12 239 968 1.234 576.0(100) (20，40，40) 8 350 858 1.187 477.0

取实例中有250 个节点的p08 至p11 数据，为检验算法在较大规模时的性能，结果如表4 所示.

表4 250 个节点的实例试验结果Table 4 Example test results for 250 nodes

表4 的结果表明:在遇到较大规模问题时，该算法仍然较快地得到了问题最优解.鉴于该算法是一种精确算法，适用性和稳定性好，而且可以具体计算出车辆调运的安排方案，这对当前大型物流或者快递公司的车辆调运安排问题的解决，具有很好的借鉴和参考价值.

4 结论与展望

作为一般车辆路径问题的扩展，本文针对对有仓库容量限制，多工厂的三层供应关系的仓库选址问题进行了研究，依据其运送特点建立了循环迭代的精确算法，这种算法在求出工厂到仓库、仓库到销售点最短路径的前提下，在满足仓库容量限制的基础上，找出可降费的闭合回路进行调整，最后再通过减少仓库个数确定最优仓库个数和运输路线，这种算法用计算机语言很容易编程实现，具有计算速度高，存储空间少等优点，并且在现实中的问题数据规模较大时，也具备较好的应用价值.

本文研究的三层调运问题，在此算法基础上只需保证相邻三层节点间调整，即可以扩展推广到N(N≥3)层运送关系的网络问题上.