特殊结构的一阶线性微分方程组的解法

朱艳玲

安徽财经大学统计与应用数学学院,安徽蚌埠,233030

常微分方程是本科数学专业的一门学科基础课，在实际中有着广泛的应用，是学习数学建模课程的先修课程之一。同时，该课程也是学习偏微分方程、微分方程定性理论、动力系统等课程的基础。长期的教学实践显示线性微分方程组的求解一直是教学的难点。对于一阶线性微分方程组，经典教材上给出的求解方法思路很清晰，详见文献[1-6]。但计算过程却很烦琐，涉及高等代数的知识较多，如矩阵的特征值、特征向量以及矩阵的逆等，同时还涉及矩阵函数的积分，导致部分高等代数基础不扎实的同学对这部分内容的学习有困难；同时发现很少有文献涉及这方面的内容。鉴于此，本文将针对几类特殊结构的一阶线性微分方程组，探讨较为简洁的求解方法，避免求矩阵的逆、特征值等较为烦琐的计算，以降低学习难度，促进学生对这部分内容的理解和掌握。

1 一阶常系数线性微分方程组

考虑如下一阶常系数线性微分方程组:

X′=AX+F(t),X(t0)=η

(1)

其中t0∈[a,b],X=(x1,…,xn)T,A=(aij)n×n,F(t)=(f1(t),…,fn(t))T为区间上[a,b]的连续函数。 对于线性微分方程组(1)，经典教材上的求解方法：先求对应齐次线性微分方程组X'=AX的基解矩阵Φ(t)，再利用常数变异法求得非齐次线性微分方程组(1)的解[1-3]：

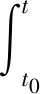
(2)

从表达式(2)不难看出，该求解方法涉及矩阵A的特征值、特征向量、基解矩阵Φ(t)的逆和矩阵的乘积等线性代数知识，同时还涉及矩阵函数的积分，过程烦琐冗长。

鉴于此，本文讨论方程组(1)的系数矩阵A具有特殊结构时的求解方法.具体如下：

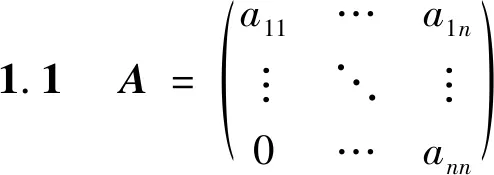
该方程组最后一个方程是关于xn一阶线性微分方程，容易求得其解，不妨记为xn=φn(t)，代入倒数第二个方程，可将其化为关于xn-1一阶线性微分方程，容易求得其解，不妨记其为xn-1=φn-1(t)，以此类推，可求出xn-2,…,x1，从而得原方程组的解。

该方程组第一个方程是关于x1一阶线性微分方程，容易求得其解，记为x1=φ1(t)，代入倒数第二个方程，可将其化为关于x2一阶线性微分方程，记其解为x2=φ2(t)，以此类推，可求出x3,…,xn，从而得原方程组的解。

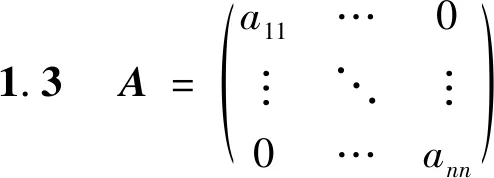
(1) 当n=2k为偶数时，可化为k个二元一阶线性微分方程组:

若fi或fn-i+1，i=1,2,…,k,可导，则上述方程组可化为关于xi或xn-i+1，i=1,2,…,k,的二阶线性微分方程：

可先求对应齐次线性微分方程的通解，然后采用试解函数法或者常数变异法求非齐次方程的通解，最后代入初值条件可求得初值问题的解。

(2) 当n=2k+1为奇数时，可化为k个二元一阶线性微分方程组：

注1 ：上述情形1.1-1.3的求解方法可以推广到系数矩阵A不是常数的情形，即系数矩阵A的元素依赖变量t，即X′=A(t)X+F(t),X(t0)=η,其中A(t),F(t)为区间上[a,b]的连续函数,显然此时公式(2)将不再适用。

2 二元一阶常系数线性微分方程组

对于二元一阶常系数线性微分方程组:

X′=BX+G(t),X(t0)=η

(3)

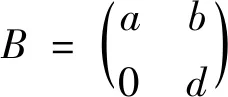
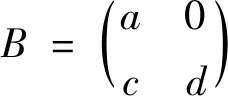
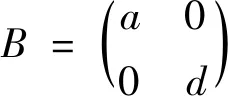
上述三种情形是微分方程组(1)当n=2的特殊情形，求解方法参照情形1.1-1.3。

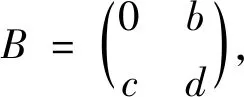
在函数f或者g可导的情形下，可划归为二阶线性微分方程求解。具体如下：

2.1.1 党参总皂苷溶解性试验。室温下，党参总皂苷在表面活性剂中溶解性排序依次为Cremophor EL40、Tween-80、Span-80；在助表面活性剂中溶解性排序依次为PEG400、1,2-丙二醇；在油相中溶解性排序依次为橄榄油、辛酸癸酸甘油三酯，故选择Cremophor EL40、PEG400、橄榄油用于确定党参总皂苷纳米乳组成。

(1)当f可导时，先对第一个方程关于t求导得x″=by′+f′(t),结合第二个方程得到关于x的二阶非齐次线性微分方程：x″=dx′+bcx-df(t)+bg(t)+f′(t);利用Euler方法以及常数变异法或者试解函数法可求得其通解x，再利用第一个方程所确定的关系式y=(x′+f(t))/b,即可求得y，最后代入初值条件，即得原方程组的解。

(2)若g可导，则对第二个方程关于t求导得y″=cx′+dy′+g′(t),结合第一个方程得到关于y的二阶非齐次线性微分方程：y″=dy′+bcy+cf(t)+g′(t);可求得该方程的解y，然后利用第一个方程x′=by+f(t)求得x；最后代入初值条件得方程组的解。

3 例子

下面举例说明上述求解方法，考虑到情形2.1-2.3，2.4和1.5的求解方法相类似，下面仅给出情形1.4-(2)，2.1和2.4的例子。

例1试求解初值问题:

(4)

解：按照情形1.4-(2)，方程组(4)等价于下面两个方程组和一个方程：

前两个方程组符合情形2.4当d=0的情形，从而按照其解法可得

解得x1=C1et+C2e-t;

x2=C3e2t+C4e-2t+et;

x4=2C3e2t-2C4e-2t+et;

x5=C1et-C2e-t

例2试求解初值问题:

(5)

解：本题属于情形2.1，第二个方程是关于y的一阶齐次线性微分方程，其满足初值条件y(0)=1的解为y=et。代入第一个方程得关于x的一阶非齐次线性微分方程：x′=x+et+e-t,从而由一阶线性微分方程的通解公式得:

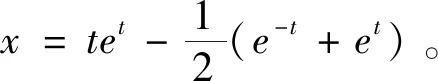
例3试求解初值问题:

(6)

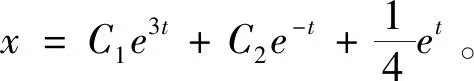
注:对比经典教材上直接利用公式(2)求解的方法，不难发现本文把具有特殊结构的线性微分方程组求解问题划归为一阶或二阶线性微分方程的求解方法，计算量小，过程简便，且涉及线性代数中有关矩阵的知识较少。这种方法大大降低了这几类线性微分方程组求解的复杂度，有利于对上述这几类特殊结构的线性微分方程组求解方法的快速理解和掌握。