基于互信息的多标记特征选择
李闪闪,潘正高
宿州学院信息工程学院,安徽宿州,234000
1 引 言
多标记学习已成为国内外机器学习领域的研究热点[1-2]。在很多实际应用中,多标记学习涉及许多高维数据。尽管从理论来说,特征越多,分类精度越高,但事实上大量的冗余特征不仅容易产生过拟合,也会扩增算法的复杂度,降低分类器的性能[3]。为了解决这一问题,大量的多标记维度约简[4]算法被提出。
多标记特征选择[5]是一种常见的多标记数据维度约简方法,其目的是从原始特征集合中,选择一组最佳的特征序列。同时,多标记学习框架中,每个对象的特征与标记数目都不再单一,因此为了研究特征与标记之间或标记集合之间的关联性,有学者将信息度量的方法引入到多标签特征选择之中。如Lin等[6]提出的基于邻域互信息的多标记特征选择算法(Multi-label Feature Selection Basedon Neighborhood Mutual Information,MFNMI),将邻域信息熵推广至多标记学习中,提出了三种新的邻域互信息的度量方法,且该算法的可行性通过实验得到了有效验证;张振海等[7]提出一种基于信息熵的多标记特征选择(Multi-lable Feature Selection Based on Information Entropy,MLFSIE)算法,其依靠特征与标记集合的信息增益评估特征的优劣,并通过设定阈值消除无关特征,从而获取最佳特征序列,但该算法并未充分探究特征间的冗余信息;Lin等[8]通过模糊互信息来评估特征重要度,提出一种基于模糊互信息的多标签流特征选择(Streaming Feature Selection for Multi-label Learning Based on Fuzzy Mutual Information,MSFS)算法,在特征空间完全已知或部分已知时,进行多标记特征选择,但该算法忽略了标记权重对特征空间的影响;基于此,林梦雷等[9]提出一种基于标记权重的特征选择方法,该方法首先利用相同特征空间下,标记对样本的可区分性给每个标记赋予相应的权重,进而根据特征对标记集合的可区分性权衡对应特征的重要程度。
尽管诸多算法很大程度上提升了多标记算法的分类性能,却也有其不足之处,或是忽略了特征间冗余性的度量,或是没有对特征与标记集合之间蕴含的相关信息进行综合分析。此外,当前多数特征选择算法均是依靠特征间的依赖关系评估特征的重要程度,而鲜少有利用特征集合之间的相似度程度作为衡量标准的。基于此,本文提出一种改进的基于互信息的多标记特征选择算法(An Improved Multi-Label Feature Selection Method based on Mutual Information-ML-ISIML),通过交叉相似度[10](Intersection)与互信息[11]14知识的有效结合,获得一组对于特征与标记集合之间具有强相关而特征集合之间存在低冗余性的特征序列。最终基于8个公开数据集上的对比实验结果表明,该算法在提升多标记分类器的性能方面是有效的。
2 相关理论
2.1 多标记学习
假设定义在实数域R上的p维样本空间X=Rp表示实例的特征属性,Y={y1,y2,…,yq}表示包含q个不同的分类标签的标签属性。给定多标记数据集D={(xi,Yi)|1≤i≤n},其中每一个xi=[xi1,xi2,…,xip]都是p维的属性向量,而Yi=[yi1,yi2,…,yiq]表示与xi相对应的一组标签向量,其中,Yi∈{-1,+1},如果xi有第k个标签,则yik=+1,否则yik=-1。多标记学习的主要任务[2]就是在给定多标记数据集D的情形下,构造一个多标记分类器f:X→2Y。使得当输入待分类的实例属性xi∈X时,分类器f能够推测出从属于该实例的类别标记集合f(x)⊆Y。
2.2 交叉相似度(Intersection)
多标记数据集特征维数太高,不仅容易增加算法的复杂度,还易造成分类精度的降低。基于以往研究很少有利用相似度矩阵评估特征重要程度的,本文利用交叉相似度的思想来实现特征选择的功能。
Intersection相似度:在统计学方法中,衡量两个分布之间相似程度的方法通常可以依靠于两个概率分布的Intersection相似度[10]。对于特征集合xi与特征集合xj之间的相似度定义为:
(1)
sim值越大,表明特征集xi与特征集xj越相似,特征集合间的冗余程度越高。sim值越小,说明特征集合之间的冗余程度越低。
2.3 互信息
(1)信息熵是随机变量不确定性程度的测度,不确定性指事件发生的概率[11]17-18,信息熵H(X)定义如(2)所示。信息熵越大,表示不确定程度越强,即集合X的不确定性程度与信息熵大小呈同方向变化。
(2)
此处,X={x1,x2,…,xm}是一个随机变量,p(xi)=P(X=xi),i=1,2,…,m则为与之对应的概率密度函数表达式。
(2)设有一对随机变量X={x1,x2,…,xm}与Y={y1,y2,…,yn},则联合熵H(X,Y)与条件熵H(Y|X)分别定义如下:
(3)
(4)
其中,H(Y|X)用于衡量集合X出现时集合Y的不确定程度的大小。并且上述公式定义满足H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)。 (3)互信息是随机变量之间相互依赖程度的一种衡量方式,因此可用于评估特征子集之间是否存在相关性以及相关程度[11]35-36。对于随机变量X和Y,其互信息I(X;Y)定义为:
(5)
此外,由熵与互信息的关系,公式(5)可以被重新定义为:
I(X;Y)=H(X)+H(Y)-H(X,Y)
(6)
或者:
I(X;Y)=H(X)-H(X|Y)
=H(Y)-H(Y|X)
(7)
此外,互信息的性质主要包含非负性与对称性。非负性即I(X;Y)≥0,当且仅当xi与yj彼此独立时取等号,而对称性则指I(X;Y)=I(Y;X),即X含有Y的信息量与Y含有X的信息量一致。
2.4 特征与标记集合的互信息
由于多标记学习中,每个样本的特征数与标记数均不再唯一,可能存在某些特征对整个标记集合的影响较小,有些特征对类别标记的判定影响较大的情形。因而,本文通过计算特征与标记集合的互信息,研究特征与标记之间的相关性。
特征x与标记集合Y={y1,y2,…,yq}的互信息定义如下[12]:
(8)
因互信息具有非负性,故IML(x;yi)≥0,若IML(x;yi)=0,表明特征与标记集合的互信息获得最小值[12],即此处特征与标记之间不存在相关性。
由公式(7)又可得:
(9)
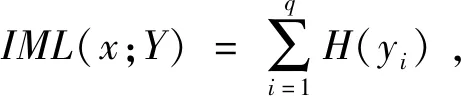
3 基于互信息的多标记特征选择
3.1 算法分析
多标记维度约简的目的是有效选择最佳的特征序列,从而提升分类器的性能。然而多数特征降维的算法,或是仅从特征之间冗余度角度出发,或是只考虑了特征与标记集合之间的相关性,均有一定的不足。又因当前极少有利用相似度方法度量特征重要度,故为了完善以上两点,本文通过相似度与互信息的有效结合,提出一种重新改进的多标记维度约简算法。
一方面,借助Intersection相似度获取特征之间具有最小冗余性的特征,另一方面,利用特征与标记集合的互信息获取与类别标记具有最大相关性的特征。故而算法公式定义如下:
fset=a×IML(x;Y)+b×sim
(10)
而相似度与互信息两者结合时,哪一方对特征选择的影响程度更高,则需要进一步衡量相似度与互信息对特征子集的影响因子。基于此,我们设定平衡参数α用来平衡两项的权重,因此公式(10)可重新写为:
fset=α×IML(x;Y)+(1-α)×sim
(11)
由于交叉相似度sim取值越小,表明特征之间冗余程度越低,该特征重要程度越高,而互信息IML(x;Y)取值越大,表明特征记集合相关性越强,该特征重要程度越高。则显而易见,sim与IML(x;Y)依据特征重要度排序时具有差异性。
因此,为了方便计算,定义para=1/sim, 此时para取值越大,特征之间冗余程度越低,此时sim与IML(x;Y)对产生的特征子集排序时较好的保持了一致性。改进后算法公式重新定义为:
fset=α×IML(x;Y)+(1-α)×para
(12)
与(10)相同,此处平衡参数α,用于控制两项目标函数中之间的权重,其取值是一个事先确定好的常量。根据公式(12)计算所得的特征进行降序排序,获取新的最优特征序列。
3.2 算法描述
综上分析,本文算法流程描述如下:
算法:ML-ISIML
输入:多标记数据集D,包含特征集合X={x1,x2,…,xn},标签集合Y={y1,y2,…,yq}
输出:最优特征子集X′={x′1,x′2,…,x′m},m (1)sim=∅,IML=∅,X'=∅; (2)for eachxi∈X (3)for eachxj∈X (5)end (6)end (7)根据第(4)步计算的特征集合之间相似度,其值越小,冗余程度越低; (8)定义para=1/sim,计算特征之间相似度的倒数,得到一组特征重要度的降序序列X′1; (9)for eachxi∈X (10)for eachyj∈Y (12)end (13)end (14)根据第(11)步计算特征与标记集合的互信息并降序排序,得到对应的特征序列X′2; (15)定义平衡参数α,计算fset=α×IML(x;Y)+(1-α)×para,并降序排序,得到一组具有强相关且低冗余性的特征序列X′。 为了验证本文算法的实验性能,本文选取了8个公开的多标记数据集:Arts, Computers, Education,Social,Society,Science,Health以及Yeast进行实验。其基本描述信息如表1所示。 所选数据集全部来自http://mulan.sourceforge.net/datasets.html. 表1 多标记数据集 实验均在3.30 GHz的处理器,2.00 GB的内存,Windows 7系统及Matlab R2012b的实验平台上运行。 实验与多标记特征降维算法MDDMspc[13]以及PMU[14]算法比较。同时实验均采用基于k近邻分类器的多标记学习算法[15](ML-kNN)处理特征选择后的数据集。ML-kNN参数设定为默认值,即平滑参数s=1,近邻k=10。 由于多标记学习系统中,每个对象都具有多个类别标签,故而此类性能评价指标和传统单标记学习相比存在一定差异。最为经典的多标记评价指标[2]主要有平均查准率(Average Precision ,AP)、覆盖率(Coverage,CO)、汉明损失(Hamming Loss,HL)、一错误率(One-Error ,OE)、排位损失(Ranking Loss ,RL)等。设有预测函数f(·,·),定义排序函数rankf(·,·),若给定多标记测试集S={(xi,Yi)|1ip},则各评价指标形式化定义如下[2]: (1)AP用于评估在全部样本的预测标记排序中,在特定标记之前的标记均被正确排列的平均分数。公式定义如(13)所示,APS(f)越大,分类性能越优,当APS(f)=1时,取得最好结果。 (13) (14) (3)HL用于评估样本标记被错误分类的次数情况,即有关标记未能被正确预测出。公式定义如(15)所示,其中Δ表示两个集合之间的对称差。HLS(h)越小,分类结果越好,当HLS(h)=0时,取得最好分类结果。 (15) (4)RL用于评估相关标记排位在不相关标记排位之后的次数情况。公式定义如(16)所示,RLS(f)越小,分类结果越好,当RLS(f)=0时,分类结果最好。 (16) (5)OE用来评估在全部样本的预测标记排位中,排在首位的标记未能被正确预测的次数情况。公式定义如(17)所示,OES(f)越小,分类性能越优,当OES(f)=0时,分类结果最好。 (17) 由于平衡参数α取值不同,会造成多标记数据分类性能的差异。因此实验首先以Yeast数据集为例,测试α取不同值的分类结果如表2所示。实验同样采用平均查准率(Average Precision,AP)、覆盖率(Coverage,CO)、汉明损失(Hamming Loss,HL)、一错误率(One-Error,OE)、排位损失(Ranking Loss,RL)5个评价指标评估算法性能。紧随每个评价指标之后的向上“↑”表示该评价指标取值越大,实验效果越好;向下“↓”则表示该评价指标取值越小,实验效果越好。表格中斜体加粗的数字则表示算法对数据集分类处理的效果更佳。 表2 平衡参数α不同取值的实验结果对比 由表2可以看出,平衡参数α取值不同时,其分类性能的确存在一定的差异。显而易见,当平衡参数α=0.9时,尽管在评价指标CV上,对应的结果略次于平衡参数α=0.1的结果,但在评价指标AP,HL,OE,RL上,对应的分类效果都要优于参数α取其他值的情形。因此,综合看来,平衡参数α=0.9时,可以取得较好的实验性能。 基于表2的实验结果,以下所有实验均是在平衡参数α=0.9的情况下进行。表3至表10分别给出在各个数据集上的算法实验结果。 表3给出基于Arts数据集的实验对比结果,可以从中看出,在评价指标OE上,ML-ISIML算法效果略次于PMU算法效果,但从评价指标AP、CO、HL以及RL实验结果看来,本文算法的实验性能均为最优。 表3 Arts数据集实验结果 表4给出基于Computers数据集的算法对比结果,可以从中看出,在评价指标HL上,ML-ISIML算法实验结果与PMU算法结果近乎一致。在其余评价指标上,ML-ISIML算法结果要优于MDDMspc、MDDMproj 以及PMU算法。 表4 Computers数据集实验结果 表5至表9分别给出基于Education,Social,Society,Science以及Yeast数据集的实验对比结果。ML-ISIML算法在5个评价指标上的取值均明显优于MDDMspc、MDDMproj 以及PMU算法。 表10给出基于Health数据集的对比结果,由表10看出,在评价指标OE上,ML-ISIML算法略次于MDDMspc算法,但在其余四个评价指标上, ML-ISIML算法实验结果均为最优。 表5 Education数据集实验结果 表6 Social数据集实验结果 表7 Society数据集实验结果 表8 Science数据集实验结果 表9 Yeast数据集实验结果 表10 Health数据集实验结果 综上所述,本文提出的ML-ISIML算法实验性能整体优于MDDMspc、MDDMproj 以及PMU算法。换言之,本文基于改进互信息多标记特征选择算法是可行的。 本文提出了一种改进的基于互信息的多标记特征选择算法。首先,利用交叉相似度的思想计算特征与特征集合之间相似度,此外,通过计算特征与标记集合之间的互信息,计算特征与标记集合之间的关联程度;最终,融合两种思想获取新的最佳特征序列。实验结果表明,本文基于改进互信息的多标记特征选择算法是切实可行的。但本文算法在一定程度上增添了实验的烦琐性,因此下一步期望提出某种优化时间性能的方法。4 实验及结果分析
4.1 实验数据
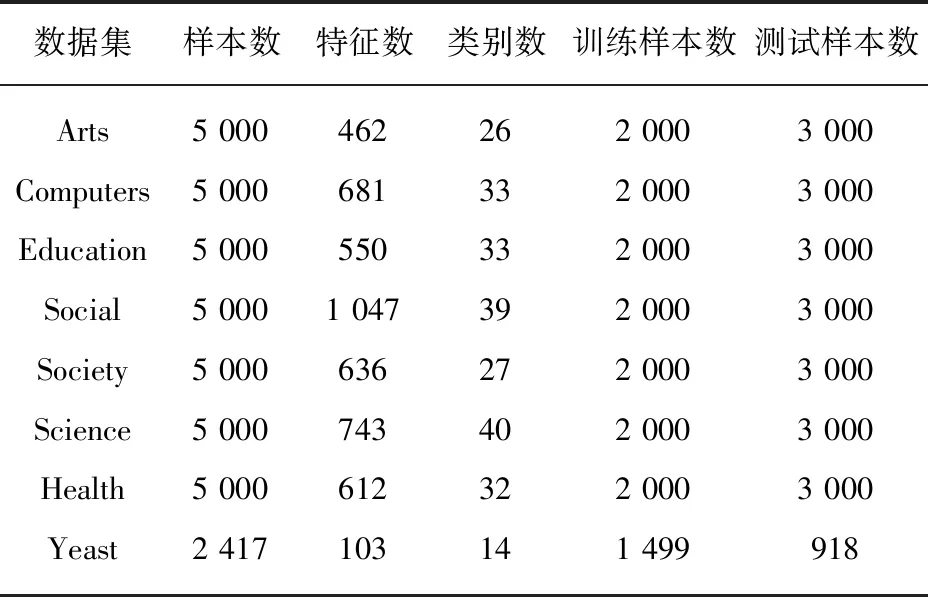
4.2 实验环境与方法
4.3 评价指标
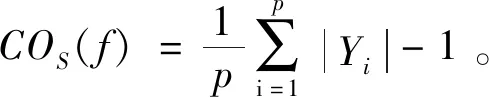
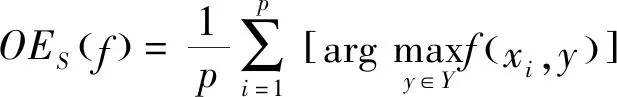
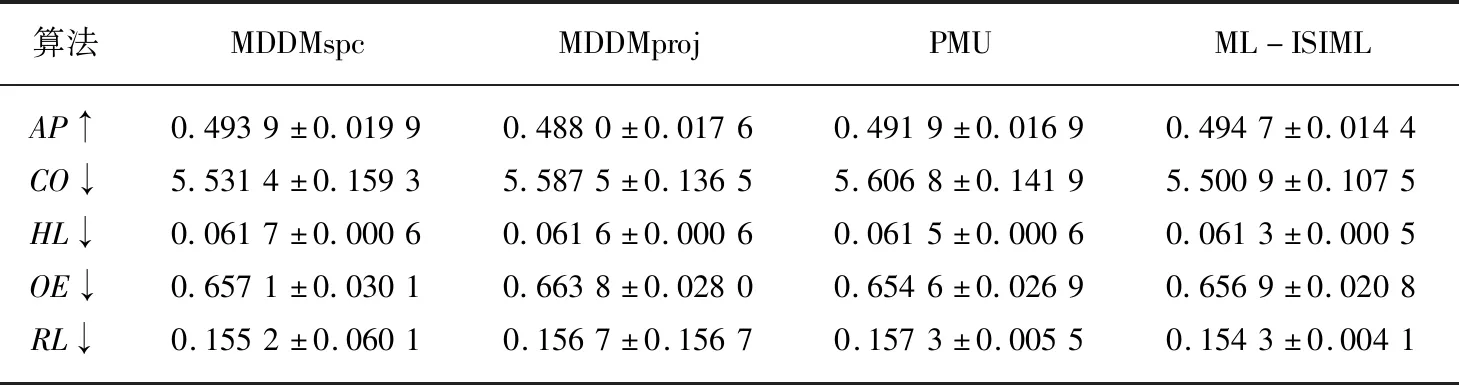
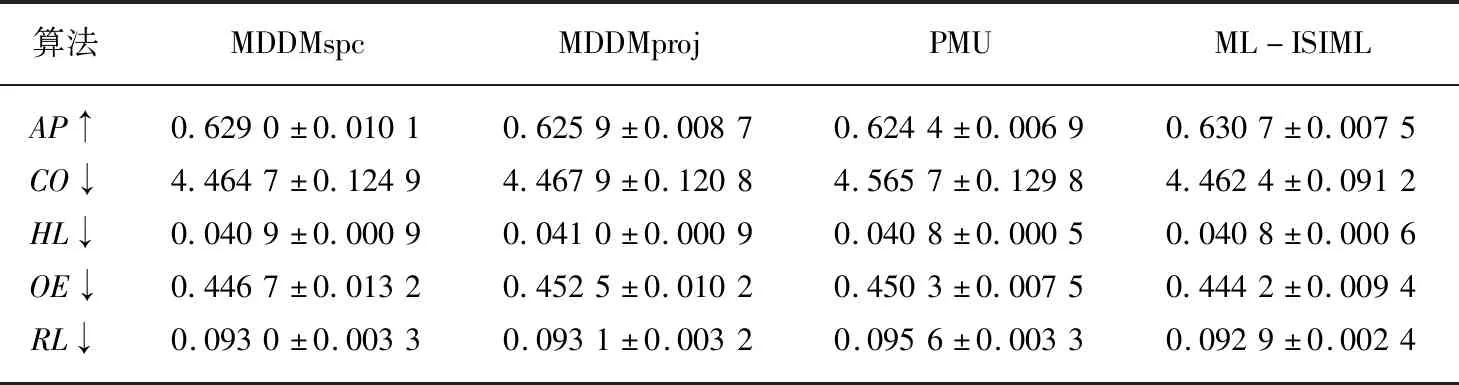
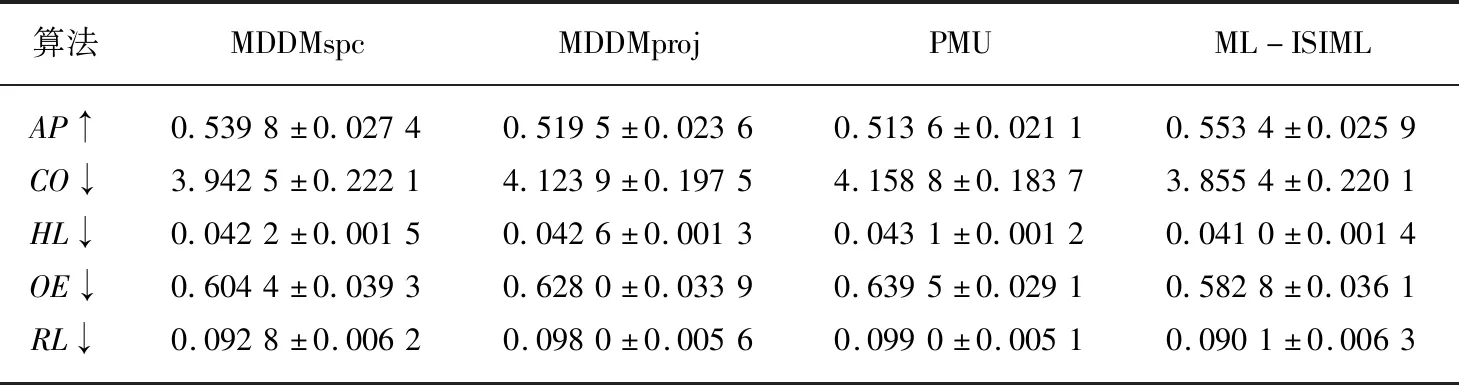
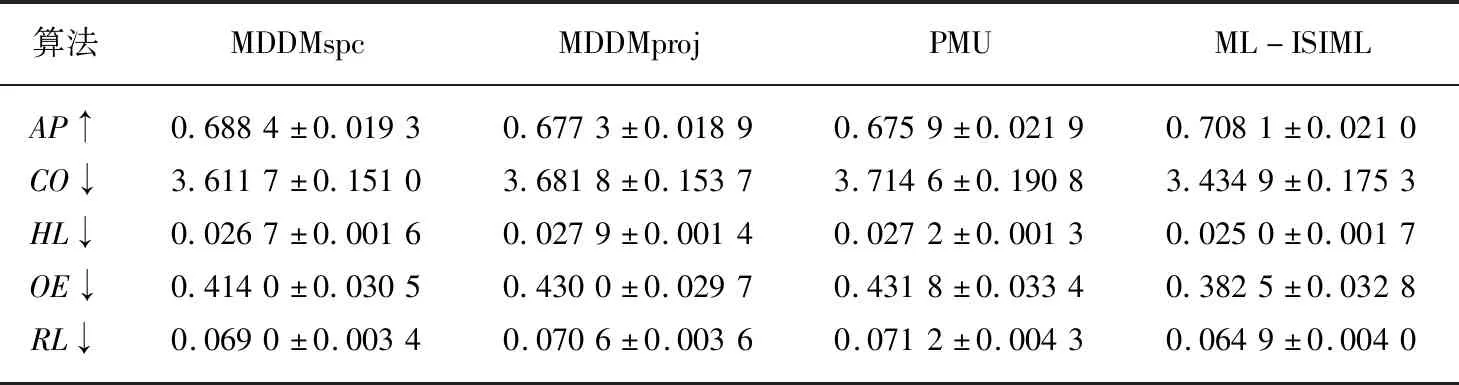
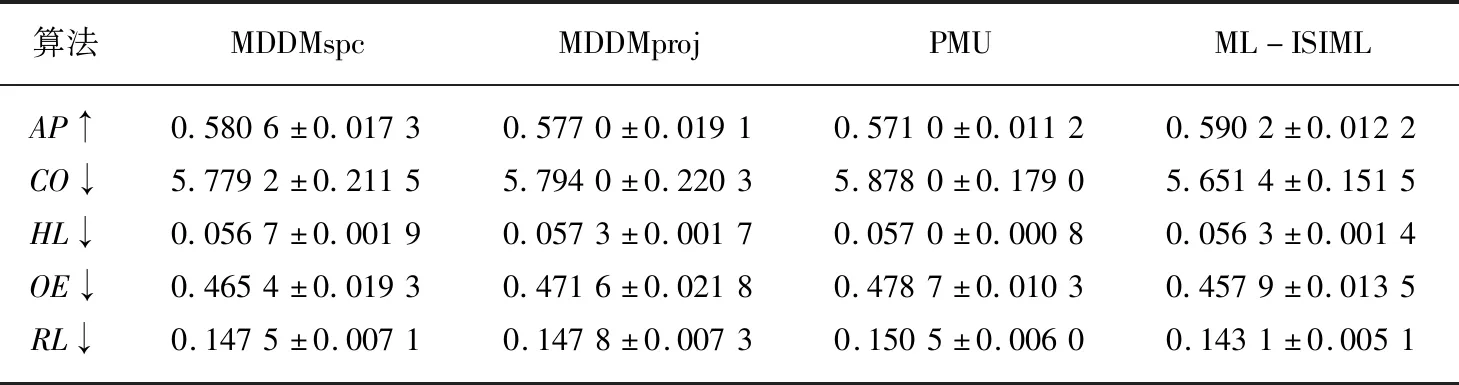
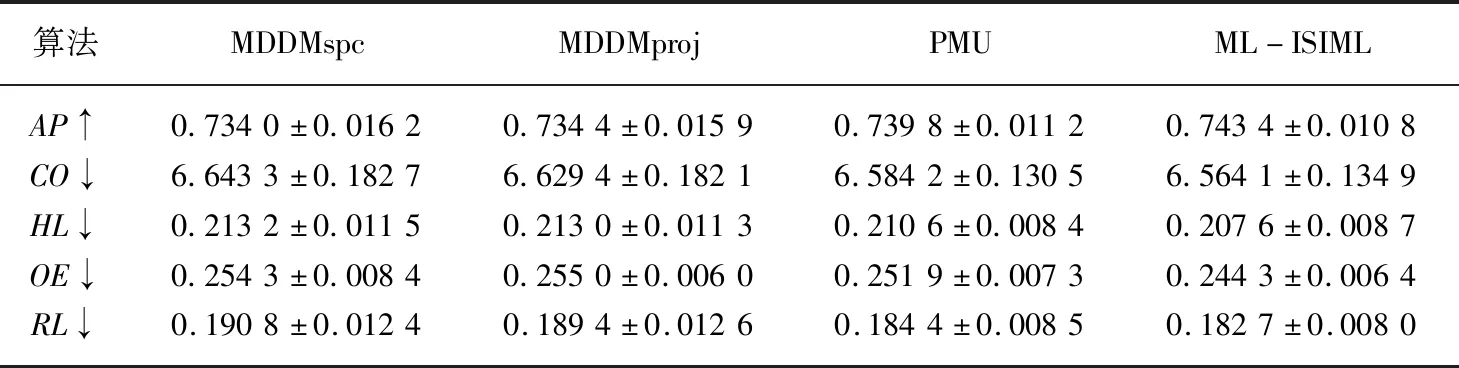
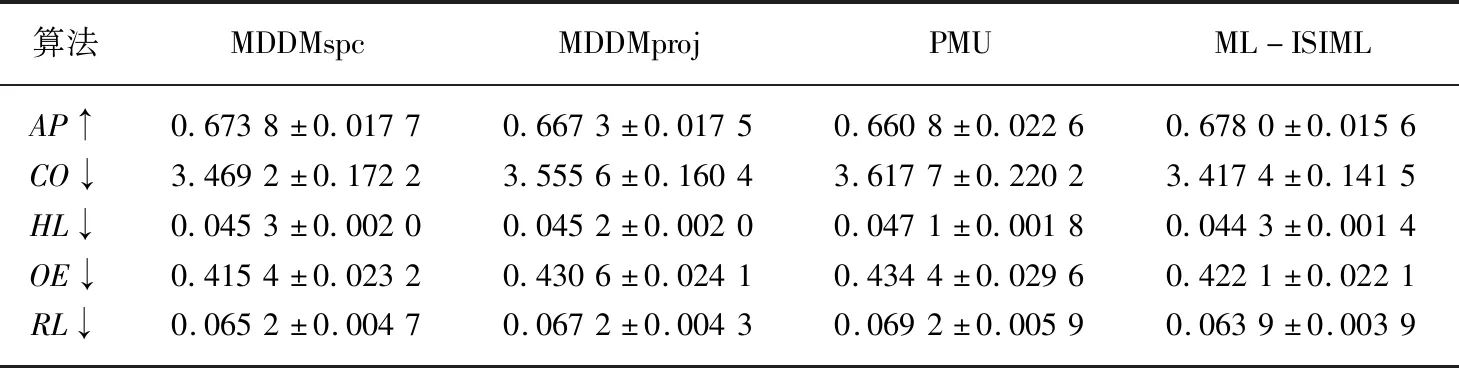
4.4 实验结果与分析


5 结 语

