用于车辆-轨道系统参数优化的分层设计与权重组合方法
徐 磊,陈宪麦
(1. 西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2. 中南大学 土木工程学院,湖南 长沙 410075)
如何实现机车车辆与线路结构之间的低动力相互作用是铁路系统动力学永恒不变的议题,而能否建立轮轨低动力作用的车辆-轨道耦合系统关系到线路安全、持续运营的时效性以及行车安全性和乘坐舒适性。铁路技术工作者针对这一问题,一方面针对机车车辆及线路结构运营过程中出现的问题进行实时改造;另一方面则是在设计阶段,便对车辆与线路的参数进行匹配设计,达到较好地轮轨低动力作用,以延长机车车辆及线路结构的使用寿命。
轮轨低动力相互作用问题早在20世纪90年代初便被科研工作者所关注[1-2]。此外,翟婉明[3]提出了采用系统设计思想实现机车车辆与线路最佳匹配设计的原理与方法;封全保等[4]利用车辆-轨道耦合动力学模型研究机车车辆和轨道结构参数对轮轨横向相互作用的影响,并提出了相关的技术措施;李小伟等[5]采用车辆-轨道耦合动力学及优化理论对轨道行驶系统的悬架参数进行优化;蔡成标等[6]对弹性支承块式无砟轨道结构的动力参数进行了优化设计;向俊等[7]对客运专线板式无砟轨道动力参数进行了优化;张剑[8]基于代理模型技术开展高速列车性能参数设计及优化工作;陆正刚等[9]建立柔性耦合单轮对走形系统的曲线通过模型,进行了曲线性能分析和参数设计原则;刘哲等[10]建立了道岔动力参数的设计方法;石怀龙等[11]基于动力吸振原理进行多个车下设备的最优悬挂频率设计,建立弹性车体和车下设备的垂向振动数学模型。
现阶段轮轨系统参数匹配设计的研究工作,主要依据车辆-轨道耦合动力学方法,单变量考察系统参数与动力学指标的关系[1-2,4,6-7],文献[3]指明了列车、线路匹配设计的基本原理,作者以之为基础,进一步融合系统动力学的基本思想:系统的行为模式与特性主要取决于其内部的结构,而且内部结构之间亦互为反馈[12],提出了一种用于车辆-轨道耦合系统参数优化的分层设计与权重组合方法,本文将具体阐述其原理、方法及应用算例。
1 车辆-轨道耦合系统参数匹配设计
从车辆-轨道耦合动力学的基本原理出发,机车车辆与线路是相互作用、相互影响的,车辆-轨道耦合系统(以下简称“此系统”)参数与动力响应通过激振源构成互为因果的动力互馈关系。换言之,在不同的激扰下,系统属性决定系统行为。对于复杂的动力系统,系统属性即为众多系统部件参数匹配后的统一表征。
此系统之动力学参数,实际上已通过车辆-轨道动力学模型相互联系与耦合。动力激扰下,参数与参数匹配后引起的系统物理力学行为可通过此模型合理考虑。所以,进行此系统低动力设计的关键,在于通过系统参数与动力响应的变化规律,寻找合理的参数匹配值(或范围)。
1.1 分层设计与权重组合原理
为了实现车辆-轨道系统低动力的最优参数匹配设计,必须从参数匹配的角度出发,参数匹配的优化程度决定了机车车辆与线路的动力匹配性能。一般而言,此系统的动力响应来源于轮轨界面的能量输入,此能量从轮轨界面出发,分别向上、下分层传递,从而引起车辆系统和轨道系统的动力响应,所以实现此系统低动力设计的基础,是降低轮轨动态相互作用。同时,如上所述,此系统的动力学行为是系统参数耦合时对系统激扰做出的反应,系统的参数与参数之间并不独立,而是相互影响、相互耦合,所以对于此系统的参数设计,必须同时考虑多参数变化下系统动态响应规律。
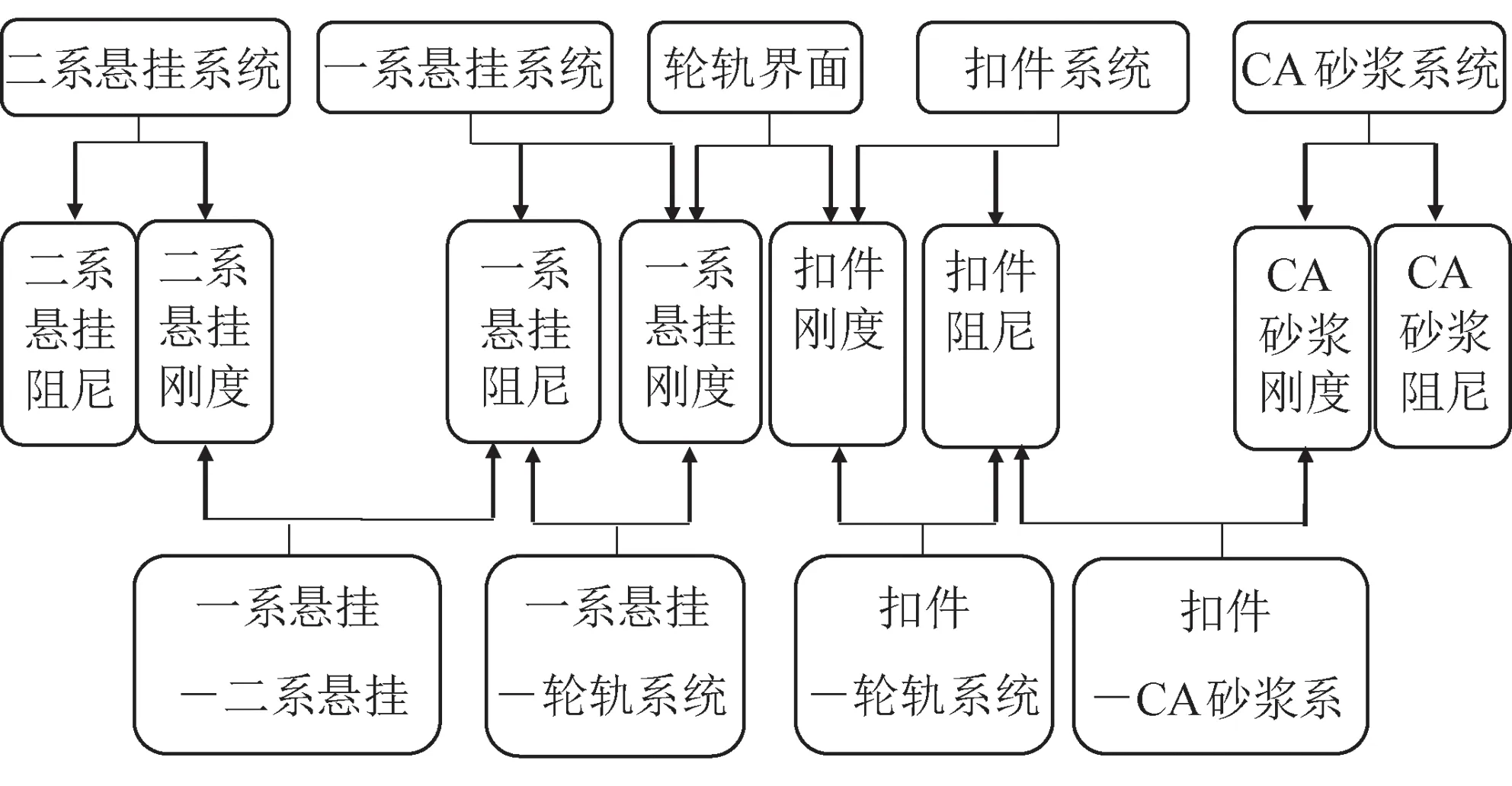
图1 车辆-轨道系统分层图
本文以车辆-轨道耦合动力学为基础,建立此系统的动力分析模型。采用分层设计的基本方法,对于高速铁路板式轨道系统而言,以轮轨界面为第一设计层,分别向上、下逐次将车辆-轨道系统离散成第二层(包括一系悬挂系统-轮轨界面、扣件系统-轮轨界面)、第三层(包括一系悬挂系统-二系悬挂系统、扣件系统-CA砂浆系统)和第四层(包括二系悬挂系统和CA砂浆系统),见图1。由图1可知,不同的参数设计层并非独立的,层与层之间均有相应的动力学参数将其耦合,如第一、二设计层通过一系悬挂和扣件刚度实现动力学参数的匹配。如此划分,是源于系统动力学的认识,即:系统内部组成要素具有互为因果的反馈特点。
与此同时,不同的系统参数在不同的设计层中,其对优化目标的动力影响程度并不一致,故而必须考虑系统参数的优化值在不同设计层中的权重问题。
1.2 分层设计与权重组合方法
在上述系统分层设计的基础上,可采用如下步骤进行系统参数的匹配设计:
(1) 运用车辆-轨道耦合动力学模型,针对不同的系统设计层,变化设计层中所属参数的幅值范围,假定其他设计层的参数不变,输入一条确定性的随机不平顺样本,进行不同参数组合下的动力响应计算。其中,常见动力响应指标见表1。

表1 车辆-轨道系统动力响应指标
(2) 采用参数两两匹配设计的方法,针对不同的动力响应指标,采用一阶前向差分法进行系统参数的敏感性曲线计算,表示为
(1)
式中:D为动力响应指标值;xτj为待优化的动力参数值;Δx为参数的分割步幅;τi、τj分别为不同的动力学参数;n为动力参数的幅值分割步数。
由式(1)可知,任意参数的敏感性曲线S(x)是考虑了同一设计层对应的匹配参数不同幅值下的动力响应平均变化结果,故而所设计出的参数对于其匹配参数而言,具有相当的稳健性。同时,由于Δx取为正值,故而S(x)为正时,表示动力响应随参数值越来越大,幅值递增时,变化率越来越大,幅值递减时,变化率越来越小;S(x)为负时,表示动力响应随参数值越来越小,幅值递增时,变化率越来越小,幅值递减时,变化率越来越大。通过S(x)便可大致描述动力响应指标随参数变化的幅值分布情况。
(3) 对于不同的动力响应指标ζi,其响应值可表示为ρζi。根据线路等级及设计目标,确定不同指标的权重系数φi。动力学分析表明,若考察某个部件的动力响应,则与其直接相关的动力参数往往影响最大,用λζi,τkj表示动力学参数τk对动力指标ζi的影响系数,j表示τk所属的设计层,λζi,τkj具体可采用下式计算
|S(xτj,m′)-S(xτj,n′)|
(2)
式中:ρζi,τkj(xτj,m)为优化值对应的动力指标响应均值;ρζi,τkj(xτj,n)为初始设计参数下动力指标响应均值;S(xτj,m′)为优化值对应的敏感性指标;S(xτj,n′)为最大的敏感性指标。
例如扣件刚度Kf在第一、二设计层中均参与了计算,若需确定影响轮轨系统指标(如轮轨力—隶属第一设计层)的最优扣件动力参数,而每一层均可定出最优设计参数Kf,j,则具体的最优扣件刚度值(或范围)采用下式计算
(3)
式中:λζ为轮轴力指标。
(4) 如此,根据参数敏感性曲线及参数组合下的动力响应指标三维分布,按照动力响应指标权重系数由大到小的顺序,优先确定权系数较大动力指标对应的较优动力参数值。对于某动力参数对此动力指标不敏感的情况,则依照权重顺序继续考察其对下一动力指标的敏感性曲线,直至获得较优动力参数。
(5) 由于不同的动力响应指标均对应一组较优的动力参数样本Ωζi,而这些样本值一般都会存在一定的差别,这便需要根据不同动力响应指标的权重φi确定最终的参数组合,可表达为
(4)
经过上述步骤,便基本可以实现车辆-轨道系统参数的最优匹配计算。
2 车辆-轨道耦合动力学模型
采用车辆-轨道耦合动力学理论,将车辆结构视为多刚体系统,轨道结构视为弹性基础。本文主要针对高速铁路进行分析,故需建立车辆-板式轨道耦合动力学模型,见图2。
车辆子系统包括车体、构架及轮对的横移、沉浮、侧滚、摇头、点头自由度,共35个自由度。
轨道子系统则采用板式轨道结构模型,取相邻扣件间距为一轨段单元,钢轨为连续点支承Euler梁,钢轨垫层为线性刚弹簧及阻尼器单元,轨道板通过CA砂浆与路基连接,CA砂浆模拟为线性均布面弹簧和粘滞阻尼器,每个轨段单元40个自由度,可表示为
(5)
式中:
δ1=[U1lR,V1lR,W1lR,θX1lR,θY1lR,θZ1lR,U1rR,V1rR,W1rR,θX1rR,θY1rR,θZ1rR,V1S,W1lS,θX1lS,θY1lS,θZ1S,W1rS,θX1rS,θY1rS]T
(6)
δ2=[U2lR,V2lR,W2lR,θX2lR,θY2lR,θZ2lR,U2rR,V2rR,W2rR,θX2rR,θY2rR,θZ2rR,V2S,W2lS,θX2lS,θY2lS,θZ2S,W2rS,θX2rS,θY2rS]T
(7)
其中,U、V、W分别为沿纵向、横向、垂向的位移;下标1、2分别为沿Y轴方向的右侧自由度和左侧自由度;下标l、r分别为沿Z轴方向的左侧自由度和右侧自由度;θ为转角位移;下标最后的R、S分别为钢轨单元和轨道板单元。
车辆子模型和轨道子模型通过动态轮轨关系进行耦合[1],即:空间接触几何关系通过迹线法求解,轮轨法向力由赫兹非线性弹性接触理论确定,切向蠕滑力则通过Kalker线性蠕滑理论求解,并经非线性修正。
本文所建立的车辆-板式轨道有限元模型,其轮轨接触几何关系及轮轨力的计算均采用文献[1]的方法,而对于车辆子系统和轨道子系统,则依据能量变分法进行建模。
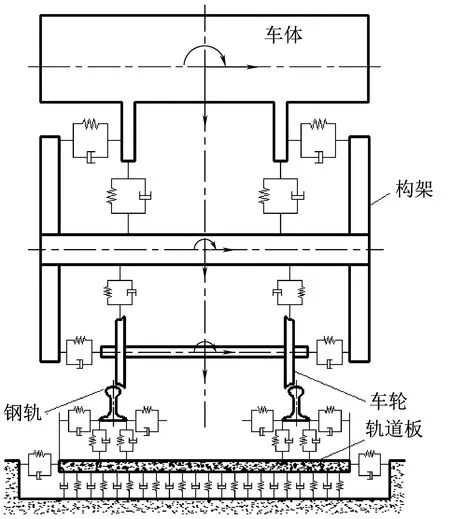
图2 车辆-板式轨道耦合动力学模型
3 算例分析
本文主要运用上述分层设计与权重组合方法实现车辆-轨道系统的横向低动力作用的参数匹配。拟优化的系统参数为车辆系统的一、二系悬挂横向刚度(Kp,y,Ks,y)、阻尼系统Cs,y,轨道系统的扣件、CA砂浆横向刚度、阻尼系数(Kph、KCAh、Cph、CCAh)。
优化参数的分层设计为
(1) 第一层:一系悬挂横向刚度、扣件横向刚度。
(2) 第二层:扣件横向刚度、阻尼。
(3) 第三层:一系悬挂横向刚度、二系悬挂横向刚度,扣件横向阻尼、CA砂浆横向刚度。
(4) 第四层:二系悬挂横向刚度、阻尼,CA砂浆横向刚度、阻尼。
动力学指标及其权重系数等级:
(1) 隶属于轮轨系统的动力响应指标,如轮轨横向力、脱轨系数、轮重减载率等,处于权系数第一等级。
(2) 隶属于车辆系统的动力响应指标,如Sperling指标等,处于权系数第二等级。
(3) 隶属于轨道系统的动力响应指标,如钢轨加速度、位移等,处于权系数第三等级。
篇幅所限,这里仅给出了以轮轨横向力和车体横向平稳性指标为优化目标时的分析过程。
3.1 以轮轨横向力为优化目标
不同设计层的参数组合下轮轨平均最大横向力分布,见图3~图6。
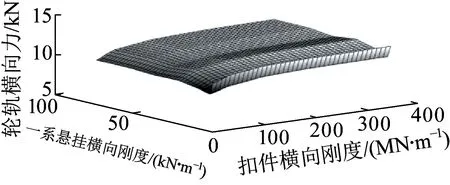
图3 不同设计层的参数组合下轮轨横向力分布曲线

图4 一、二系悬挂横向刚度扣件横向刚度及阴尼在不同设计层的敏感系数曲线

图5 第三层设计(扣件横向阻尼-CA砂浆横向刚度)
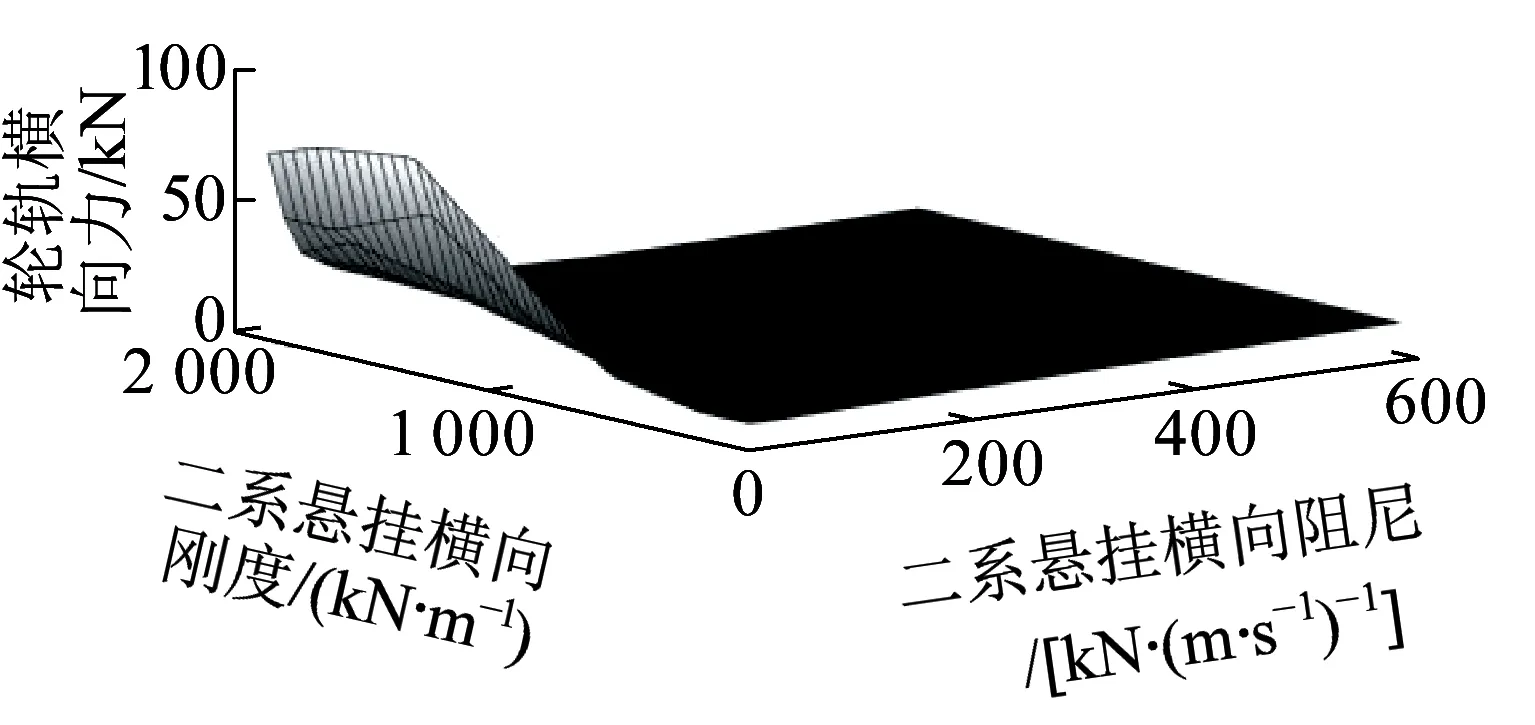
图6 第四层设计(二系横向刚度-二系横向阻尼)
由图3~图6可知,对于不同的设计层,可以提取最小轮轨横向力对应的参数组合。但对于参数组合中的层间连接参数(如扣件横向刚度为第一、二设计层的连接参数),其优化值在不同的设计层中会有所变化,故此设计值一般为局部最优值。根据上文,除第四设计层的CA砂浆横向阻尼及二系悬挂横向阻尼外,所有的待优化参数均在不同设计层参与动力计算,起着层与层之间动力属性的纽带作用,故而参数的设计必须考虑此参数在不同设计层的动力敏感性,见式(2)。
图7~图10给出了一、二系悬挂横向刚度、扣件横向刚度及阻尼在不同设计层的敏感系数曲线。

图7 一系悬挂横向刚度敏感曲线

图8 扣件横向刚度敏感曲线
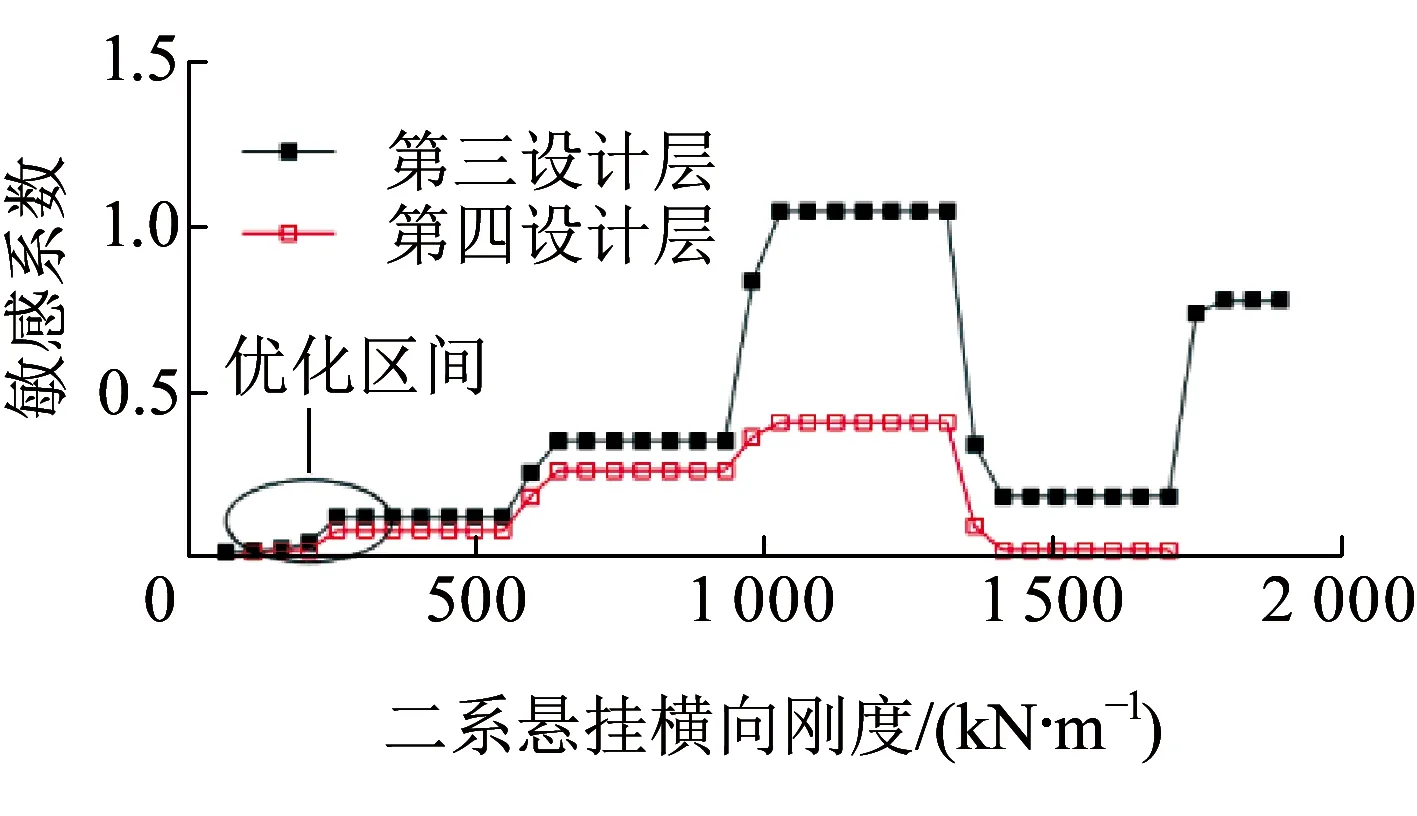
图9 二系悬挂横向刚度敏感曲线
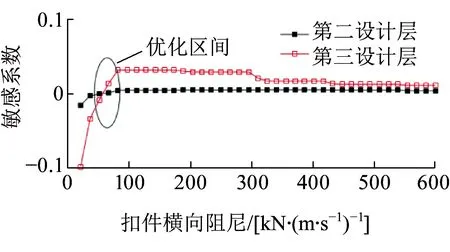
图10 扣件横向阻尼敏感曲线
由图7~图10可知,作为轮轨系统的核心动力指标,轮轨横向力对第一设计层的一系悬挂横向刚度和扣件横向刚度均具有较强的敏感性。在参数的两两联合分析中,一系悬挂横向刚度存在一个最优的区间范围为2.64~10.24 MN/m,超过此范围,将不利于降低轮轨横向相互作用力;扣件横向刚度越小,越有利于降低轮轨横向相互作用力,可取范围为12.38~30.15 MN/m;二系悬挂横向刚度对轮轨横向相互作用影响很小,较优取值范围为162.80~546.60 kN/m;扣件横向阻尼亦存在一个较优取值区间36.46~66.92 kN/(m·s-1)。上述研究结果与文献[4]基本一致,但又有所不同。如图9所示,在第四层设计中,二系悬挂横向刚度对轮轨横向相互作用几乎无影响;而在第三层设计中,通过与一系悬挂横向刚度进行匹配计算,可知其刚度过大时,亦对轮轨横向相互作用亦甚是不利,这也是需要进行参数匹配的分层设计原因之一。
根据计算结果获得的其他参数的优化区间,见表2。

表2 其他横向动力参数的优化幅值区间
需要指出的是,上述最优取值范围是以轮轨横向力最优化目标而获得的计算结果。若以其他动力指标为优化目标,其最优范围又将有所不同,此时需要采用式(3)进行参数的权重组合计算。以脱轨系数为优化目标,扣件横向阻尼优化区间的示意见图11。
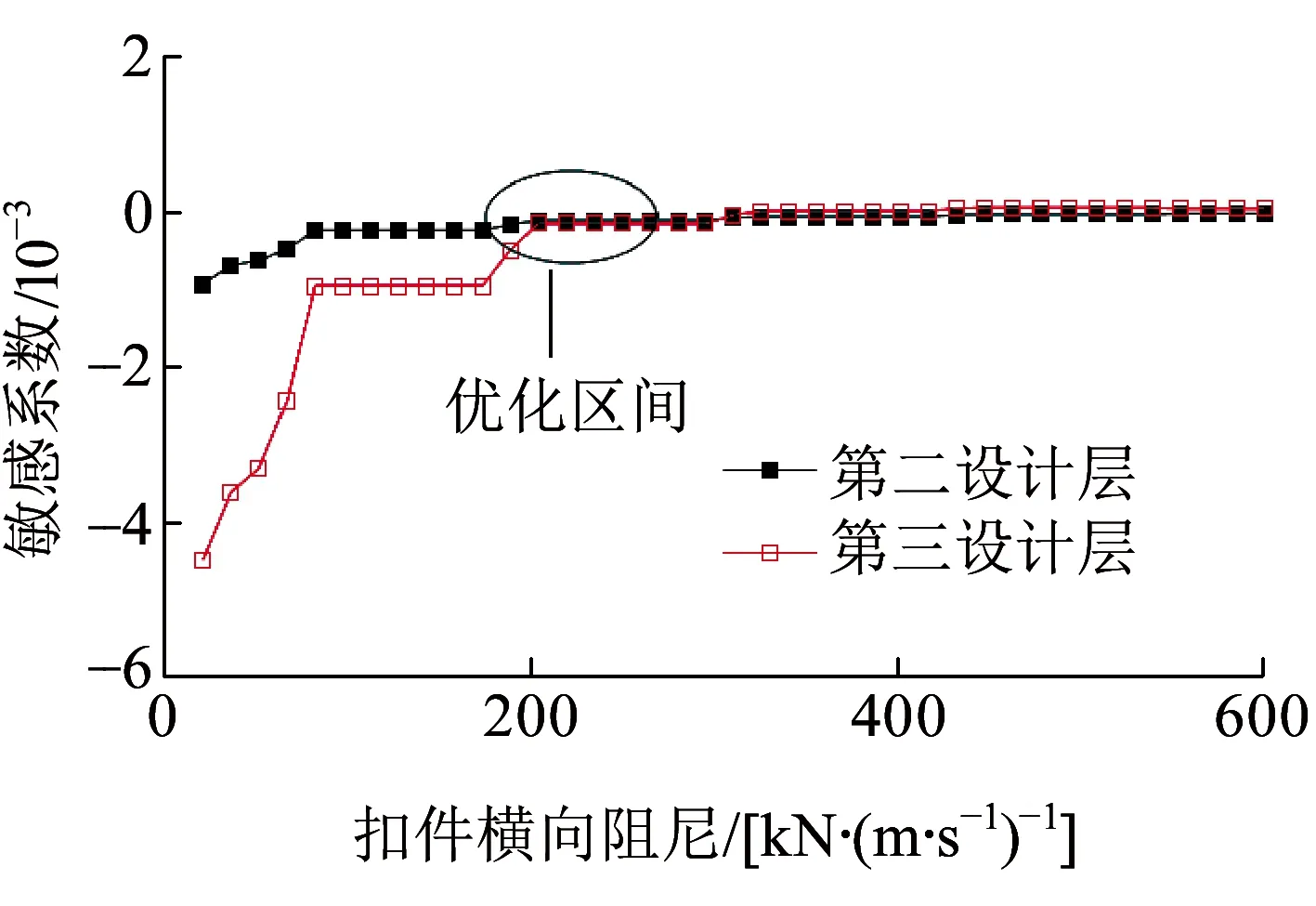
图11 扣件横向阻尼敏感曲线
将图11与图10进行比较分析,可知其优化区间有所变化,向相对高阻尼范围偏移。但考察其敏感系数,可知此动力参数对脱轨系统并不敏感,故其权重可取相对的小值。
3.2 以车体横向平稳性指标为优化目标
图12~图15给出了以横向平稳性指标为优化目标,一、二系悬挂横向刚度、扣件横向刚度及横向阻尼的敏感曲线。

图12 一系悬挂横向刚度敏感曲线
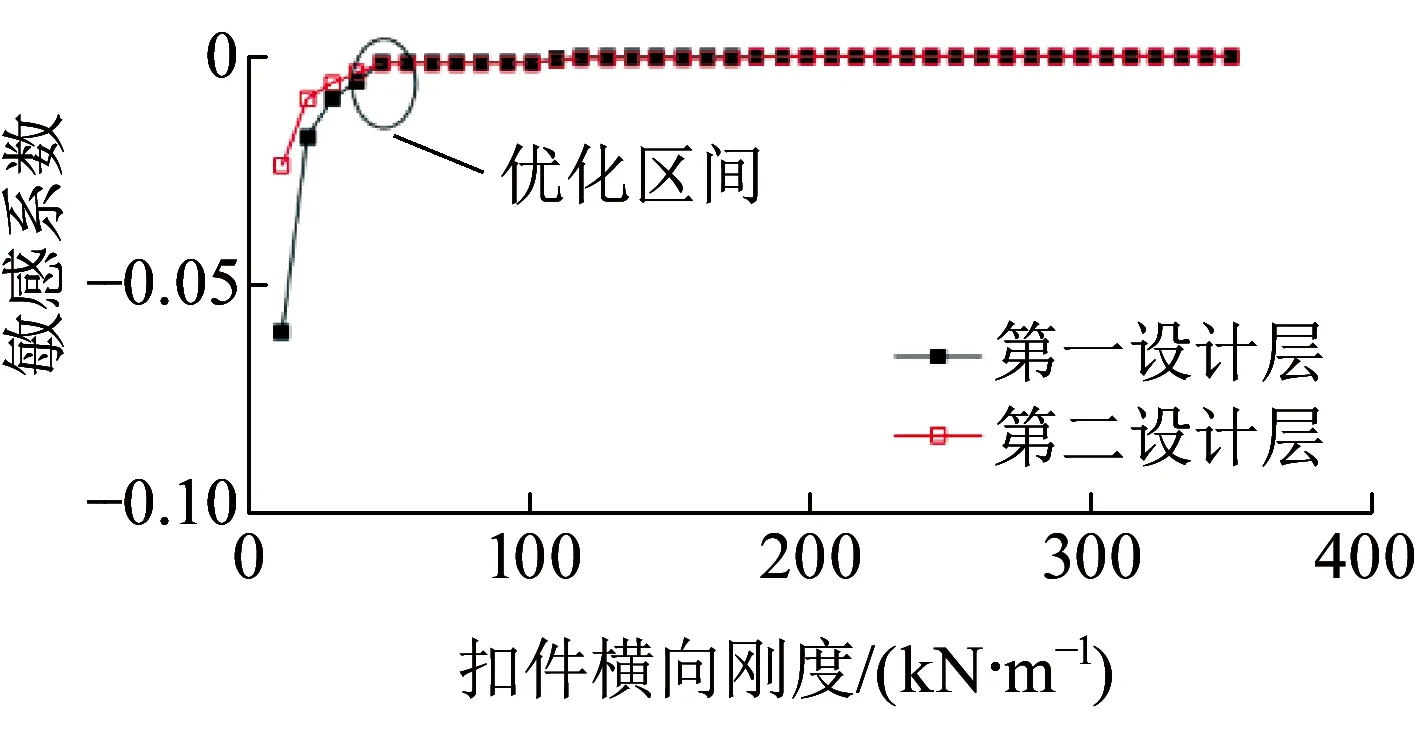
图13 扣件横向刚度敏感曲线

图14 二系悬挂横向刚度敏感曲线
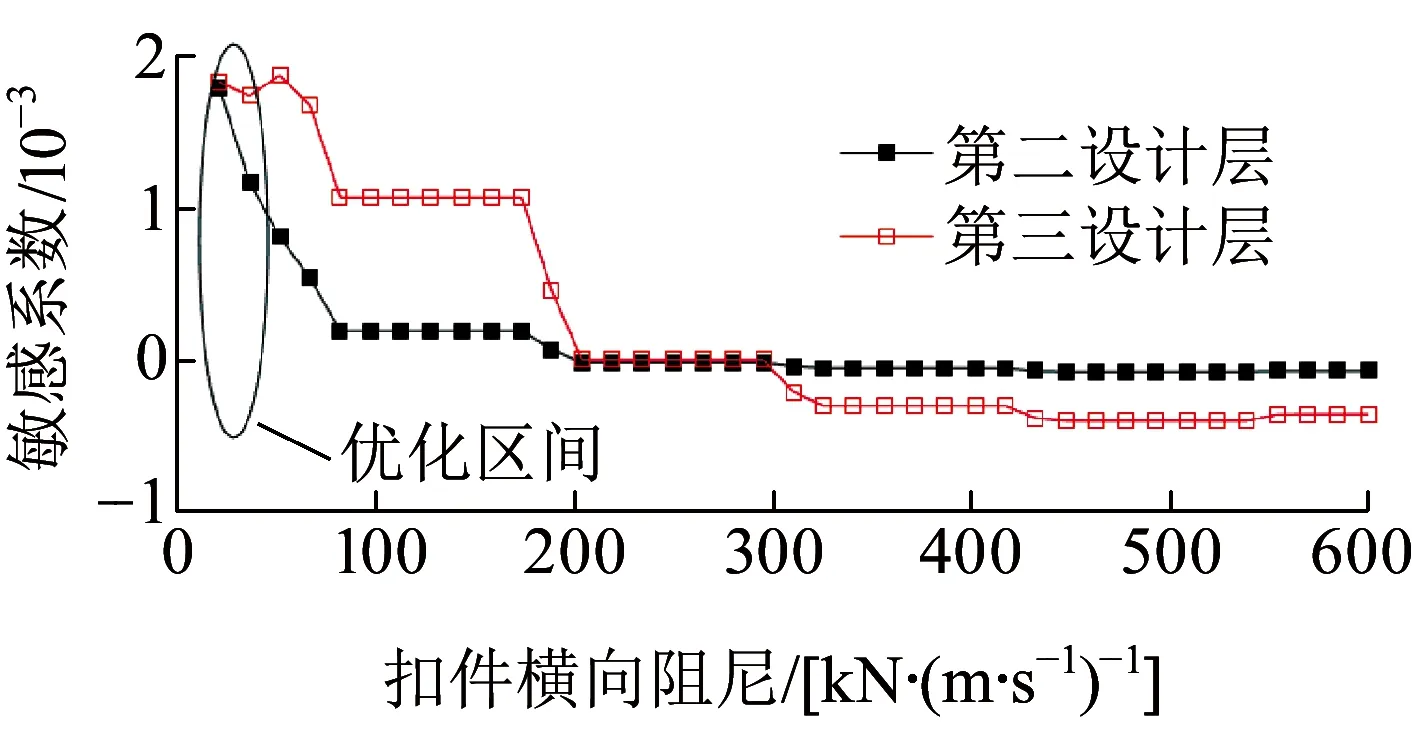
图15 扣件横向阻尼敏感曲线
由图12、图13可知,当以车体横向平稳性指标为优化目标,不同动力参数的最优区间又将有所不同,一系悬挂横向及扣件横向刚度随参数值的增大,对应的车体横向平稳性指标减小,当到达一定参数值后,基本对车体横向平稳性无影响,这些变化趋势与图7、图8明显不同,故而需要根据不同动力响应指标的权重进一步优化指标范围;可确定最优区间分别为10.24~21.63 MN/m、30.15~47.92 MN/m。由图14可知,较小的二系悬挂横向刚度有利于提高车体横向平稳性,另外,稍微提高二系悬挂的横向阻尼亦有利于提高车体横向平稳性(见图16),这些结果与文献[5]的优化结果相一致,二系悬挂横向刚度及阻尼的优化区间可分别取为114.9~162.8 kN/m、170.1~199.9 kN/(m·s-1)。由图15可知,扣件横向阻尼对车体横向平稳性敏感系数很小,说明其影响很小,其阻尼减小可提高车体横向平稳性。
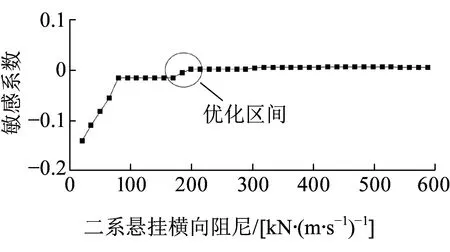
图16 二系悬挂横向阻尼敏感曲线
3.3 优化结果
依据上述步骤可逐步获得不同动力指标对应的最优横向动力参数值,限于篇幅,这里直接给出本文的优化参数,见表3、表4。

表3 车辆参数优化结果

表4 轨道参数优化结果
依次采用上述优化前、后的动力学计算参数进行车辆-轨道耦合的动力学计算,不同动力指标的对比分析见表5;典型优化结果见图17。
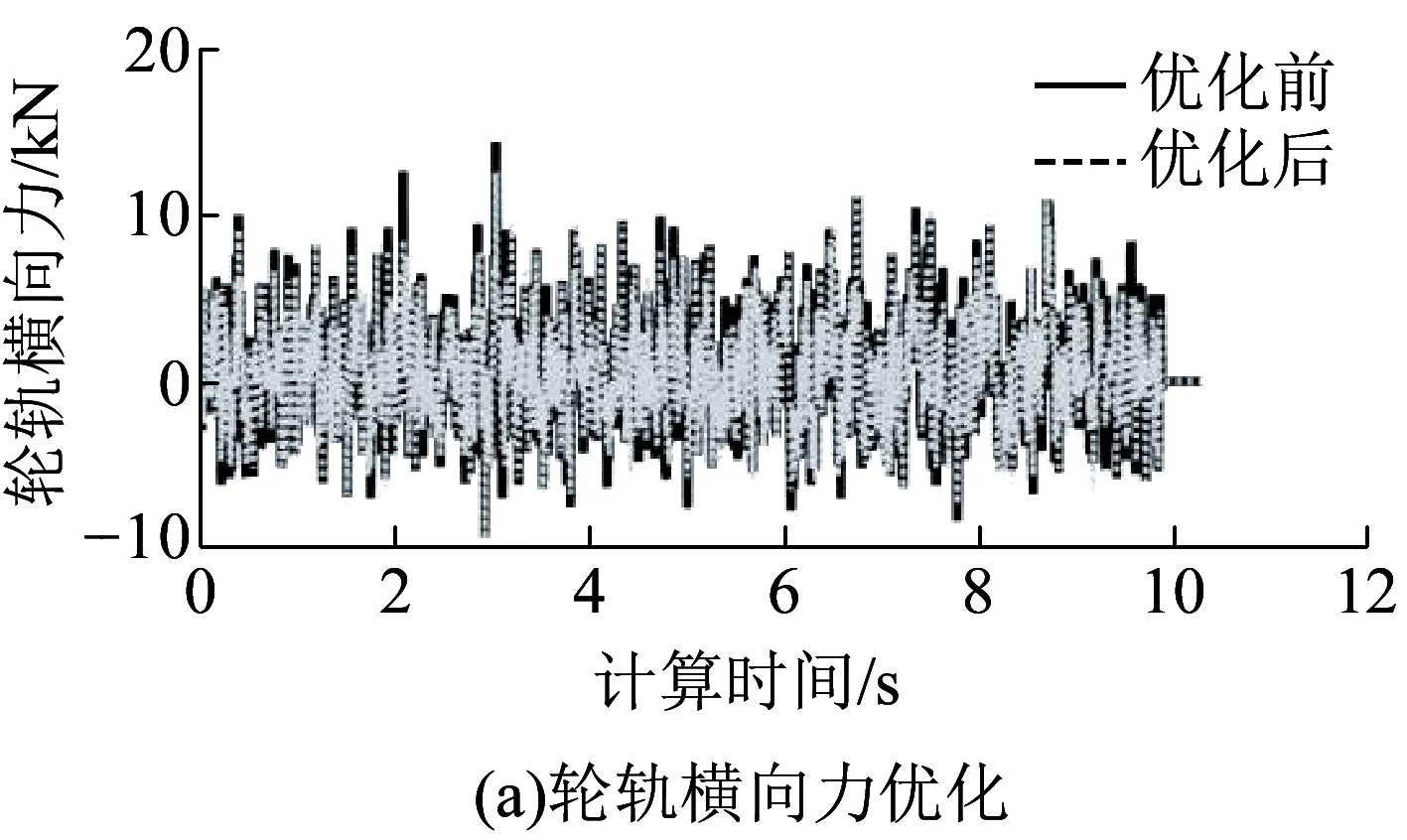

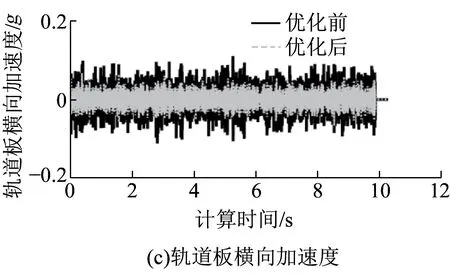
图17 典型动力指标的计算时程优化
由表5及图17可知,采用分层设计与权重组合方法对车辆-轨道耦合系统的横向振动参数进行优化的效果是较好的,各项横向动力学指标均显著减小,且并未对其垂向振动性能产生较大影响(除车体垂向振动加速度略有增加外)。
4 结论
(1) 基于机车车辆与线路的最佳匹配设计原理,进一步引入系统动力学的基本思想,突破了以往参数设计过程中孤立考察单一系统参数与动力响应关联规律的思路,采用一种新的分层设计与权重组合方法进行车辆-轨道耦合系统的低动力参数优化,算例证明了方法的有效性。
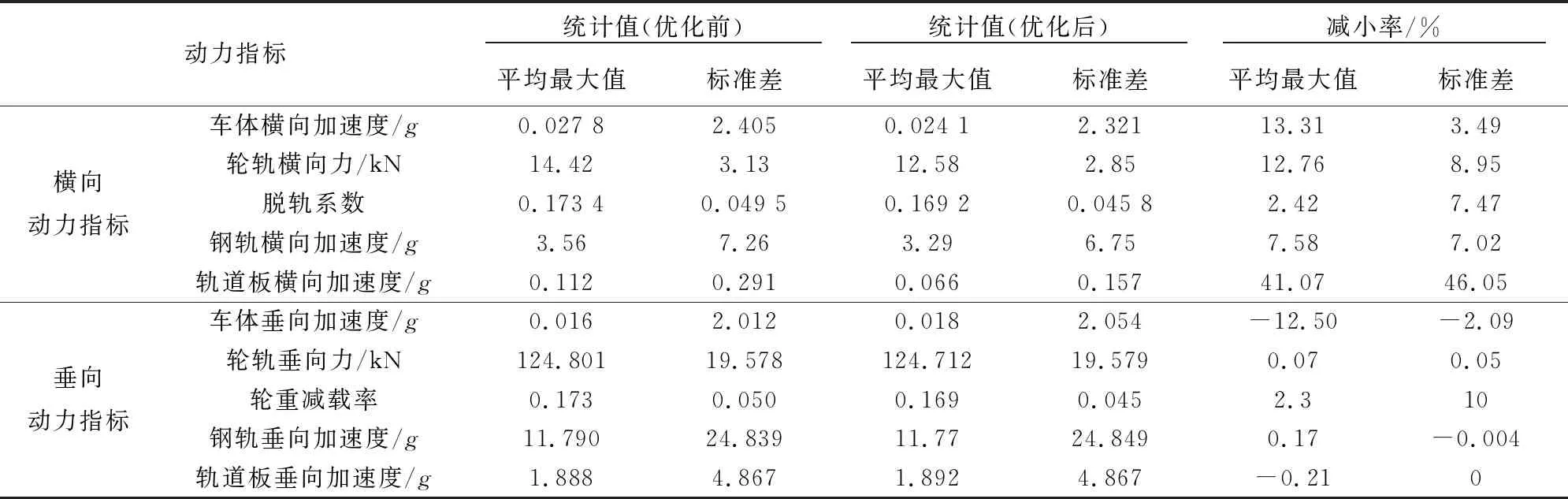
表5 参数优化前后的动力指标比较
(2) 对于车辆-轨道耦合系统的参数匹配设计,不仅限于分析系统参数与其动力响应的关联规律,还应考察系统参数与参数之间的相互耦合性,这在以往的系统设计中尚未充分考虑。
(3) 本文提出的分层设计与权重组合方法是十分简单易行的,给出了较为明确的设计思路与流程,可供铁路科技工作者参考。

