基坑开挖引起临近盾构隧道剪切错台变形计算研究

魏 纲，俞国骅，张 佳，张治国，王立忠

(1. 浙江大学城市学院 土木工程系，浙江 杭州 310015；2. 安徽理工大学 土木建筑学院，安徽 淮南 232001；3. 上海理工大学 环境与建筑学院，上海 200093；4. 浙江大学 建筑工程学院，浙江 杭州 310058)

随着城市轨道交通越来越普及，在既有地铁隧道旁进行基坑开挖的工况也越来越多。当基坑开挖时，其周围土体会产生附加应力，使得基坑旁边的既有盾构隧道产生附加的应力和变形，导致隧道衬砌环之间发生开裂和错动，影响地铁的正常运营。相关管理条例[1]对地铁结构的变形与位移有着严格的限制规定。所以，需要针对基坑卸荷开挖对临近隧道的影响进行专项研究，以探明其作用机理。

目前对于上述问题，国内外学者的研究方法主要可归纳为：现场实测[2-3]、数值模拟[4-5]、理论计算[6-10]和离心模型试验[11]。在理论计算方面，文献[6-10]将盾构隧道简化为一根材质均匀、轴线方向连续的地基梁的做法与实际情况有所出入。实际盾构隧道管片接头处的力学特性突变，直接影响到盾构隧道的变形性能，不可忽略。而在文献[12]中用剪切弹簧来模拟盾构隧道管片之间的螺栓连接的方式就更为合理。但在文献[12]中基坑坑底应力完全释放且不考虑侧壁应力释放的建模假设存在不足之处，卸荷基坑在其四周与底部都设有围护与支撑结构，会阻挡坑底与基坑侧边部分的应力传递，所以在这一方面需要进行优化。

文献[13]中建立了一个基坑开挖力学模型，计算了基坑开挖引起的临近盾构隧道附加荷载，并验证其合理性，但没有计算隧道的水平位移。所以本文基于文献[13]建立的基坑开挖力学模型，对文献[12]的计算方法进行了修正，考虑了基坑侧壁的卸荷效应和坑底围护结构的“遮拦效应”，求解地铁盾构隧道的水平位移、错台量及环间剪切力值，对盾构隧道的安全进行评估，并与实测结果进行对比分析，验证了本文的计算方法在目标工况下的合理性。

1 基坑卸荷产生的附加应力计算

依据文献[14]可知，基坑开挖卸荷主要引起临近盾构隧道的水平向位移，所以本文的研究重点就放在计算盾构隧道的水平向位移。而竖向位移较小，可不作考虑。本文采用两阶段的研究方法，先计算基坑开挖时在盾构隧道轴线上产生的应力，再计算盾构隧道的位移值。

建立一个临近盾构隧道的基坑开挖模型，基坑长度为L、基坑宽度为B，基坑开挖深度为d，坐标轴建立方式见图1。分别给出坑底和基坑侧壁卸载在隧道轴线处产生的土体附加应力计算公式。

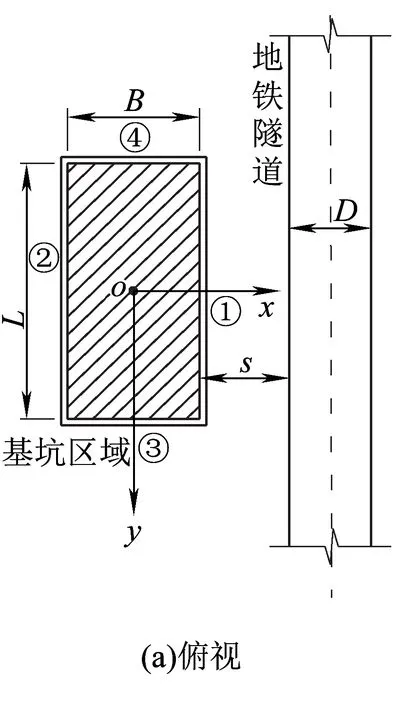
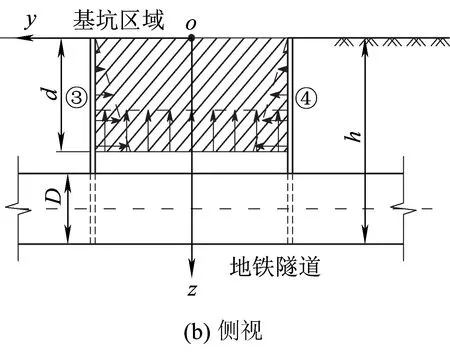
图1 基坑开挖对旁边隧道影响的计算模型

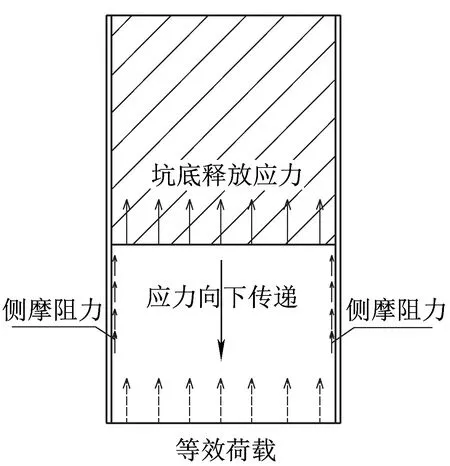
图2 围护结构底面处的等效荷载

1.1 坑底卸荷应力计算

基坑底部释放的应力在向下传递时，会受到基坑侧向围护的影响，传力路径见图2，其等效荷载为

(1)

式中：qs1为平均侧摩阻力，qs1=c+(γd+γH)/2·K0tanφ；γ为重度；d0为基抗开挖面底部至基坑围护结构底面的距离；φ为土体内摩擦角；c为土的黏聚力；α为残余应力系数[14]

(2)

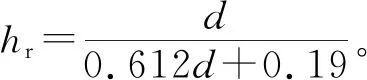
(3)

1.2 基坑侧壁卸荷应力计算

(4)

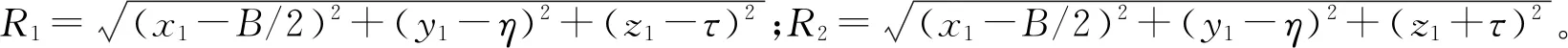
(5)

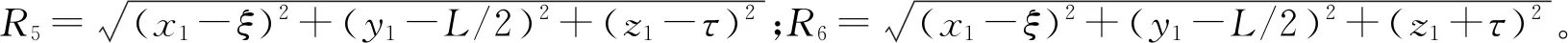
(6)

1.3 土体总的附加应力

将基坑卸荷在盾构隧道轴线处产生的水平附加应力进行相互叠加，可以得到盾构隧道轴线上一点(x1，y1，z1)土体的水平总附加应力σx为

(7)

2 盾构隧道纵向水平变形计算

2.1 盾构隧道剪切错台模型

为了更加真实地模拟盾构隧道在受外力作用时的变形情况，将盾构隧道管片之间的连接用剪切弹簧来进行简化，使得盾构隧道的变形按照剪切错台的方式进行(见图3)，与实际相吻合。经多位学者[15-16]验证，该简化模型能较好反映盾构隧道变形特征。

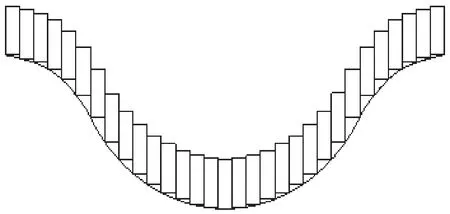
图3 隧道环间错台变形示意

2.2 运用能量变分法计算隧道水平位移量

2.2.1 盾构隧道的总势能

最小势能原理最早应用于盾构隧道施工对地下管线的影响，这种计算方式不需要经过复杂的迭代运算，即可达到要求精度，所以本文引入这种计算方法，计算盾构隧道在基坑开挖工况下的水平位移。取一环盾构环片，将其编号为m，环宽δ，该环受到的荷载为

F=P(y)-kDS(y)-kt(ΔWm+1+ΔWm)

(8)

式中：kDS(y)为地基抗力计算公式，k为地基基床系数，采用Vesic[17]公式计算；P(y)为盾构隧道受到的附加荷载，P(y)=Dσx；地基弹簧的位移S(y)与隧道的水平位移W(y)相一致；kt(ΔWm+1+ΔWm)为环间剪切力值，kt为隧道的环间剪切刚度。

盾构隧道每环管片受到多个力的作用，经分析计算得到盾构隧道的总体势能，各部分势能分析如下：

(1) 基坑开挖时产生的附加荷载对盾构隧道做功为

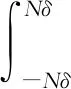
(9)

式中：2N为受影响的盾构隧道衬砌环数。

(2) 假定地基基床系数为恒定数值，则盾构隧道克服地层抗力做功为

(10)

(3) 假定剪切弹簧的刚度为恒定系数，盾构隧道克服环间剪力做功为

(11)

由式(9)～式(11)可得到盾构地铁隧道的总势能为

(12)

2.2.2 假设隧道衬砌环的位移试函数

能量变分法的关键在于寻找合适的位移函数来表示盾构隧道的变形曲线。文献[12]的位移试函数包含正弦和余弦两个部分，本文经研究后发现该函数拟合效果不是很理想。研究发现文献[18]提出的位移试函数拟合效果较好。因此，本文假设隧道位移试函数[18]如下，并按傅里叶级数展开

(13)

式中：

A={a0al…an}T

B={b0bl…bn}T

其中，A、B均为假设的位移函数中的待定矩阵；n为级数展开阶数，展开阶数越高，最终求得的位移量就越精确。

2.2.3 变分控制方程

将总势能Ep对各待定系数作偏微分方程求解，即

(14)

式中：ξi为待定矩阵A、B中的各个元素。

对上式求解可得到方程

[Tn(m+1)δ-Tn(mδ)]+

(15)

将式(15)表达为矩阵形式为

(16)

式中：Kt为盾构隧道管片环之间的刚度矩阵

[Tn((m+1)δ)-Tn(mδ)]

Ks为盾构隧道所在地层的土体刚度矩阵

其中，Pn为由于基坑开挖产生的附加荷载对盾构隧道管片的作用效应

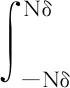
(17)

由式(13)计算可得到系数矩阵A、B中的各个元素，代回盾构隧道位移试函数W(y)，就可以得到盾构隧道的受到基坑开挖影响而产生的水平位移值。

错台量ΔW为

ΔW=W[(m+1)δ]-W(mδ)

(18)

环间剪切力Q为

Q={W[(m+1)δ]-W(mδ)}×kt

(19)

傅里叶展开阶数取10阶，即可满足计算精度，以上公式通过Matlab进行编程计算。

3 工程实例分析

采用本文方法对2个临近隧道的基坑工程进行分析计算，得到盾构隧道受到基坑开挖的影响而产生的水平位移值，并与实测曲线进行了对比，具有较好地工程适用性。

3.1 基坑工程案例1

杭州某基坑工程，基坑平面开挖尺寸L为68 m，开挖宽度B为72 m，基坑开挖深度d为16.4 m，基坑的长边与地铁盾构隧道平行，水平相距13 m，盾构隧道直径为6.2 m，盾构环间的剪切刚度kt=4×105kN/m，盾构隧道的等效抗弯刚度EtIt=1.087×108kN·m2，隧道底部埋深为17.05 m，隧道位于③层粉质砂土中，根据地勘报告，该层土的弹性模量Es取25 MPa，土的重度γ取18.5 kN/m3，泊松比μ为0.35，静止土压力系数K0取0.53；盾构管片每环宽δ取1.2 m，N取200。在该工况下，基坑侧壁应力损失率β取12%。

研究表明：当基坑开挖深度比较小时，基坑坑底以下围护结构深度也较小，此时坑底卸荷对旁边隧道产生较大影响；当基坑开挖深度较大时，基坑坑底以下围护结构深度也较大，此时“遮拦效应”明显，坑底卸荷对旁边隧道几乎不产生影响。本案例的开挖深度为16.4 m，相对较深，影响几乎为零，故不考虑坑底卸荷效应，仅计算侧壁卸荷效应。案例2情况相同。

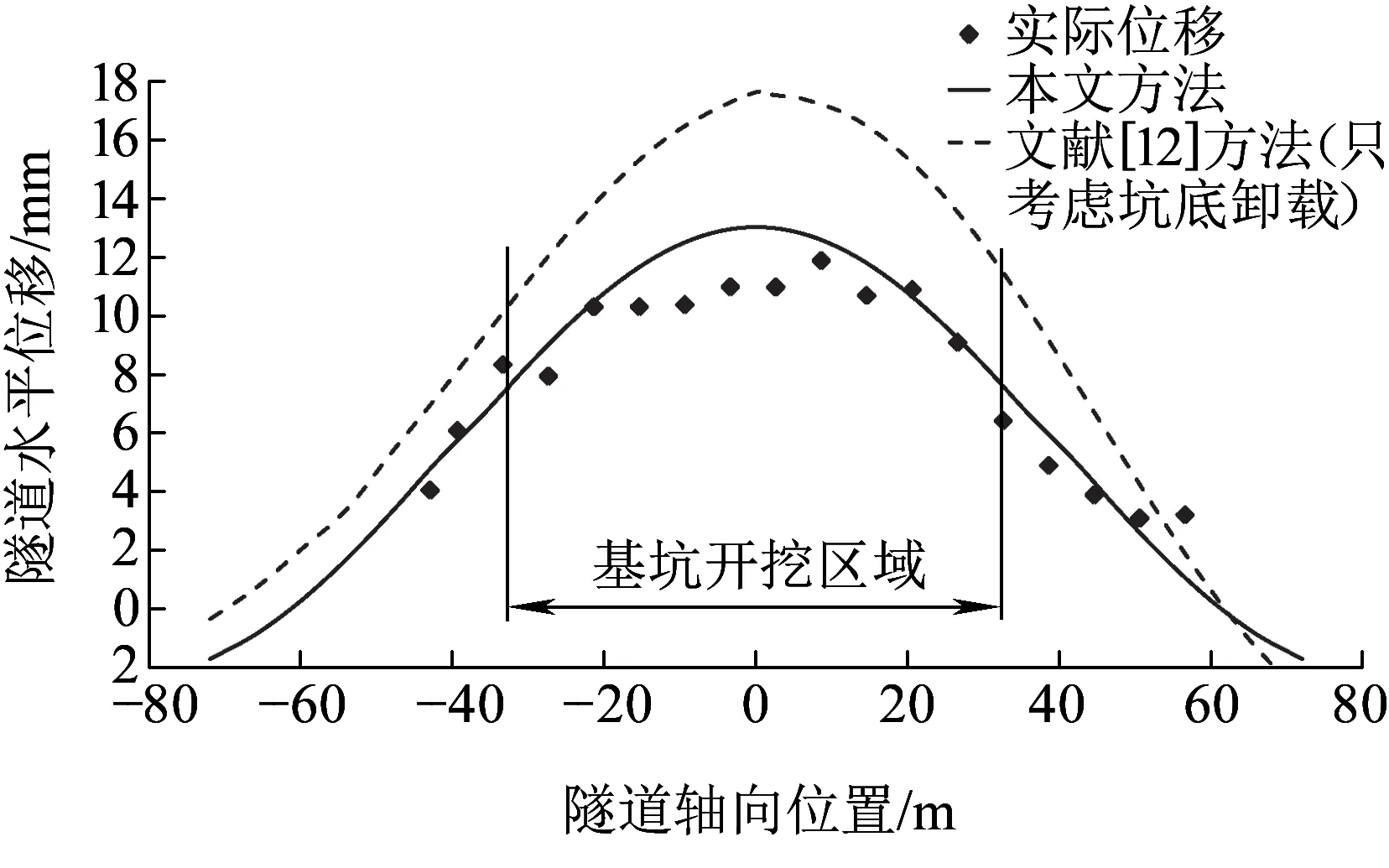
图4 工程实例1隧道水平向位移对比

图4为两种计算方法对同一工程案例进行分析计算，最后与实测值相对比的结果。

从图4中可以看出：(1)本文计算得到的盾构隧道水平位移值与实测值较为接近，盾构隧道的水平向的变形曲线总体呈现正态分布状。(2)最大水平位移实测值为11.9 mm，本文计算得到的最大水平位移值为13.0 mm，相差1.1 mm。而另一种方法计算得到的位移曲线，虽然在整体变化趋势上与实际情况保持一致，但在位移最大值方面要远远超过实测值，原因在于文献[12]的理论假设中没有合理考虑基坑围护体系对卸荷应力传递的影响，导致计算得到的盾构隧道轴线处的附加应力偏大，进而影响到最终水平位移值的计算。文献[12]这类计算假设更适合于沉井类基坑工程。

采用本文方法计算得到的基坑各个侧壁卸荷所产生的盾构隧道水平位移曲线见图5。由图5可知：(1)由于侧壁①卸荷产生的盾构隧道水平位移占到隧道总水平位移的97%，占比最大。(2)由侧壁③、④卸荷产生的盾构隧道水平位移都较小，在位移图上表现为关于纵轴对称。(3)在这个工况下，坑底卸荷对盾构隧道的影响几乎为零，由于坑底和侧面围护结构的影响，没有在盾构隧道轴线处产生附加应力，也没有使得盾构隧道发生位移形变。

从本文的计算结果恰好与文献[12]中假设相反，即基坑侧壁卸荷对临近盾构隧道产生较大影响。

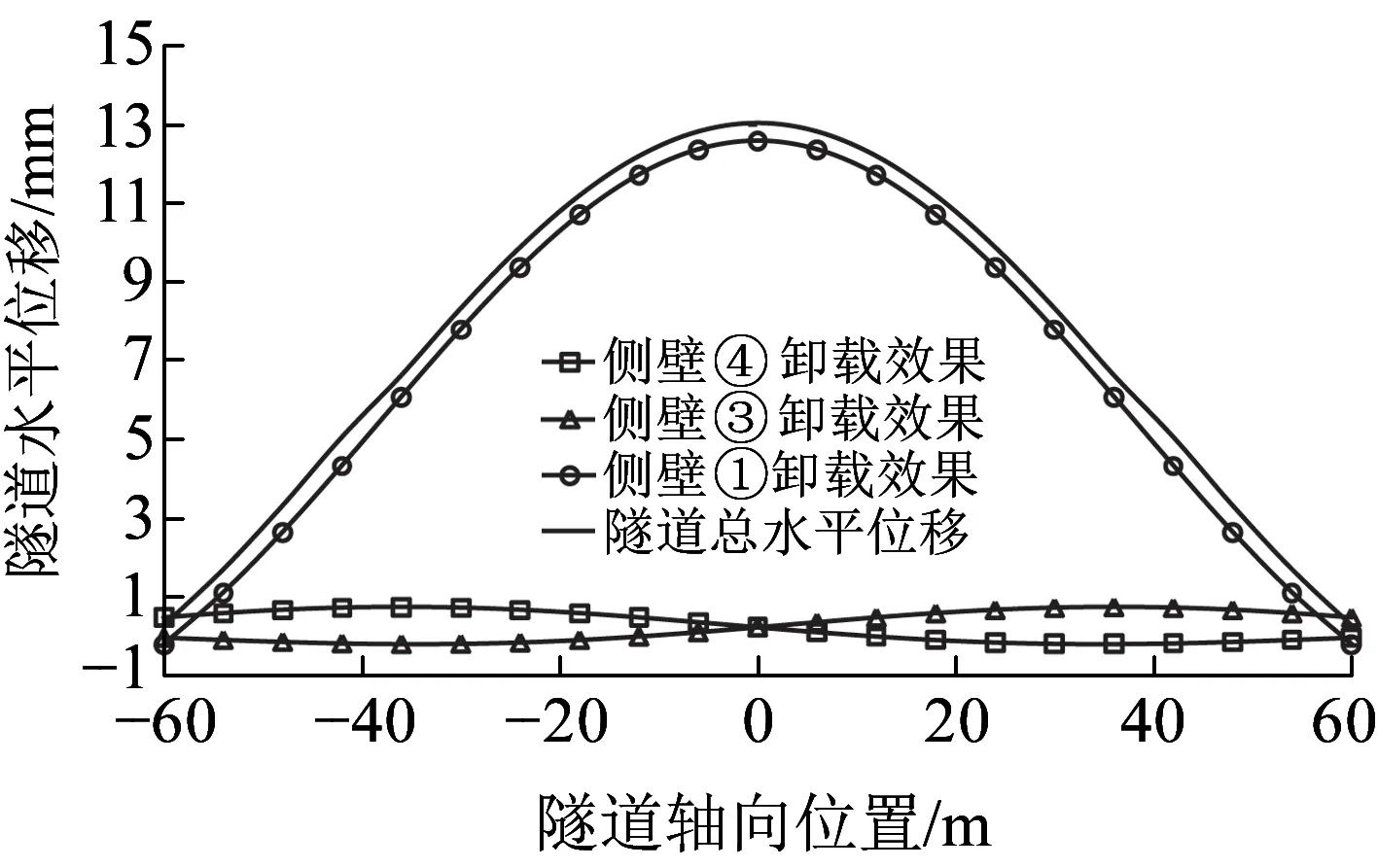
图5 基坑侧壁卸荷引起隧道水平位移曲线

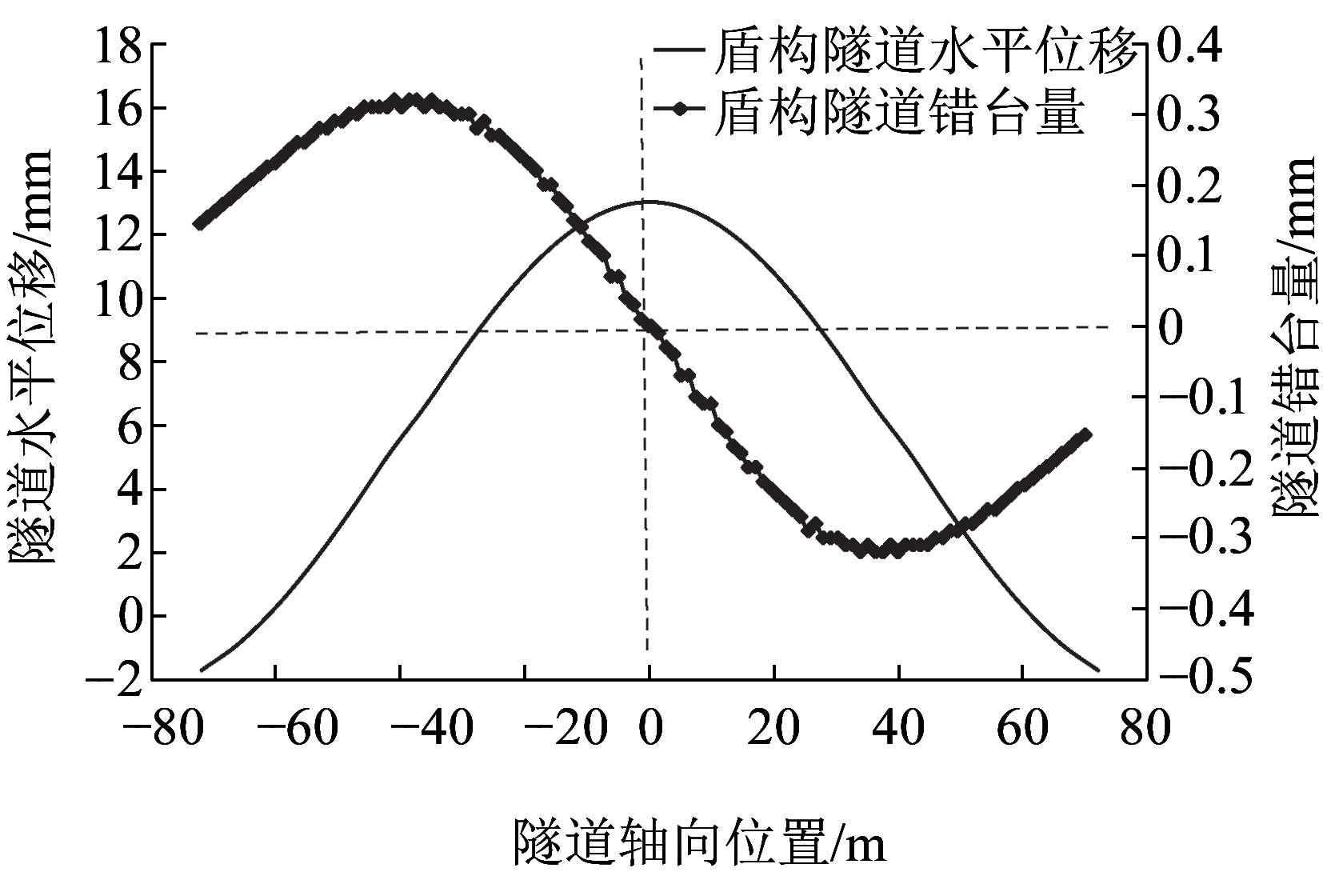
图6 工程实例1中盾构隧道环间错台量

盾构隧道的环间错台量作为地铁隧道日常的检修维护中一个重要的检查项目，是关系到盾构隧道防水体系及结构的安全，为了有效预测隧道能否正常运营，对于盾构隧道环间错台量进行计算。本文方法计算得到的环间错台量见图6，由图6可知：(1)盾构隧道水平位移最大值处的隧道管片没有发生相对错动，只发生了整体平移。(2)在水平位移曲线曲率最大处即曲线反弯点处，盾构隧道的错台量为0.32 mm。

按照本文的计算方法，还可以计算盾构隧道各环环间剪力值及其分布情况，计算结果见图7，由图可知：盾构隧道环间剪力值与盾构错台量成正比，剪力最大值为128 kN，位于环间错台量最大处。本工程中，盾构隧道环间极限剪切强度为665.36 kN，所以该位置仍处于安全范围内。

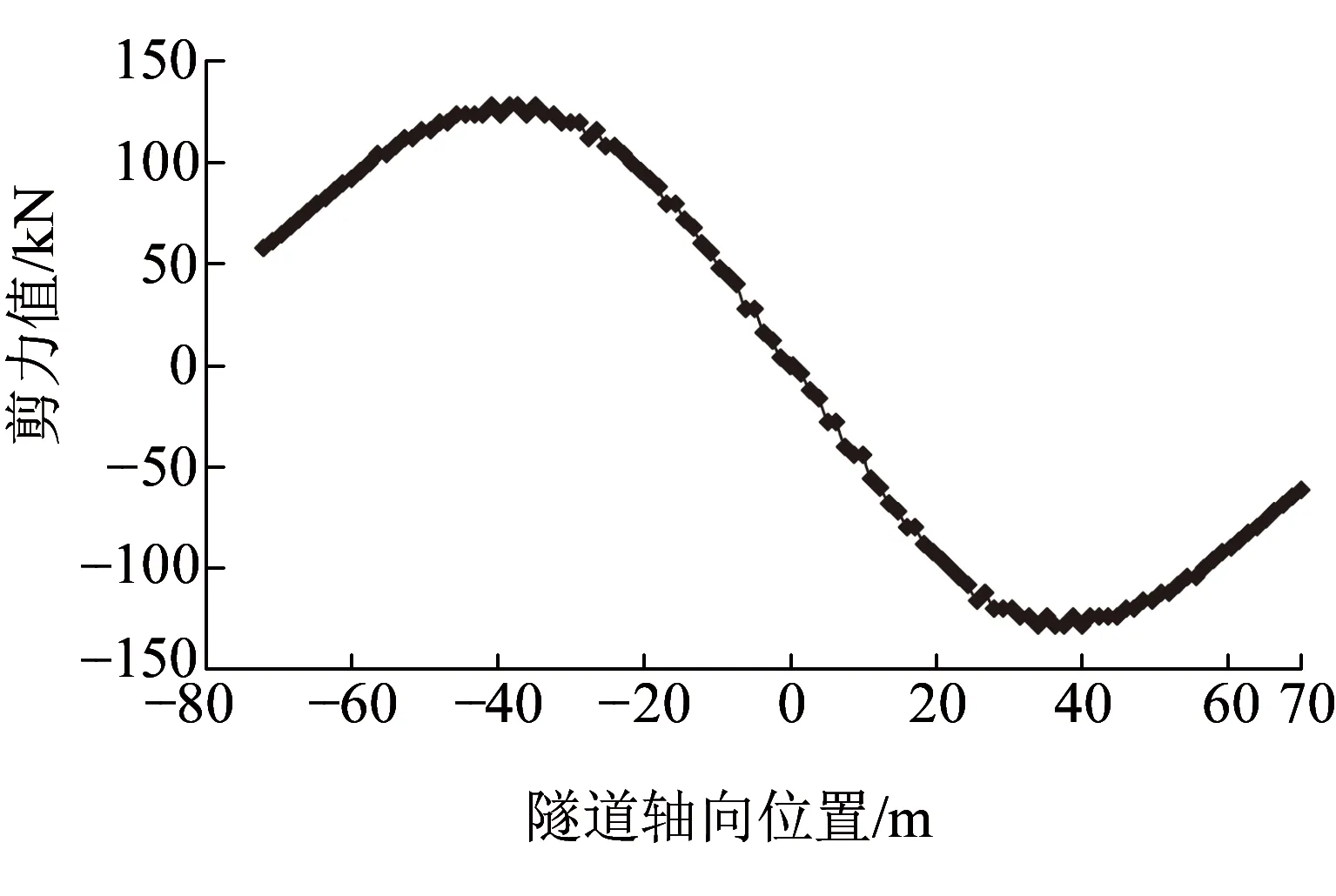
图7 工程实例1的隧道环间剪切力值

3.2 基坑工程案例2

某基坑工程临近上海地铁1号线的平面开挖尺寸如下[19]：基坑开挖宽度B为42 m，基坑开挖长度L为70 m，基坑开挖深度d为10 m。盾构隧道平行于基坑长边，隧道与基坑相距10.3 m，盾构隧道直径D取6.2 m，盾构环之间的剪切刚度kt=4×105kN/m，盾构隧道的等效抗弯刚度EtIt=1.087×108kN·m2，盾构管片每环宽δ取1.2 m，隧道底部埋深为13.2 m，盾构隧道位于②-3砂质黏土和④层淤泥质黏土中，按照实际地勘报告，盾构隧道所处土层弹性模量Es=25 MPa，静止土压力系数K0=0.53，土的重度γ取18 kN/m3，泊松比μ取0.35；N取150，在该工况下，基坑侧壁应力损失率β=10%。

盾构隧道水平位移曲线对比见图8，由图8可见，本文计算得到隧道水平位移曲线与实测值变化规律以及峰值情况都非常接近。而周顺华等[12]得到的水平位移曲线虽然在变化规律上与实测值一致，但在具体位移数值上就有所出入。

图8 工程实例2隧道水平向位移对比

图9 工程实例2的隧道错台量

本文方法计算得到盾构管片错台量见图9，在水平位移最大值处几乎不发生盾构环之间的相互错动。由于实测数据有限，不能在该曲线上看出错台量的峰值情况。

盾构隧道的环间错台量通过积累产生了隧道纵向的水平位移，所以在实际工程中要对盾构隧道的位移值和环间错台值进行及时测量与监控。本工程的隧道环间剪切力变化规律和工程1有类似，这里不再赘述。

4 结论

(1) 本文考虑了基坑围护对卸荷应力传递影响，修正了文献[12]中由于基坑开挖而产生的附加应力计算方法，指出其论文中有关坑底与侧壁应力释放假设的缺陷之处。本文方法计算得到的盾构隧道位移与实测值在变化规律和峰值情况上都比较吻合，可用于实际工程中盾构隧道水平位移、错台量和环间剪切力值的预测，以此来保障隧道运营安全。

(2) 通过计算发现由于基坑围护对应力传递路径的影响，基坑底部卸荷对隧道水平位移的影响非常小；靠近盾构隧道的基坑侧壁卸荷造成的隧道水平位移在总水平位移中占比最大；盾构隧道水平位移最大值处的管片的错台量几乎为0；隧道最大环间错台量和剪切力值都出现在水平位移曲线斜率最大处即反弯点附近。

本文并没有研究隧道最有可能渗漏的位置和隧道结构最薄弱位置在何处；同时计算参数β和N的取值也需要作进一步研究，需要通过更多的实际案例进行验证；文中在计算坑底卸荷与侧壁卸荷对盾构隧道产生的影响时，对采用的侧摩阻力以及应力分布作了简化，建议可作进一步研究。