基于粒子滤波联合算法的地磁室内定位

黄 鹤 ，仇凯悦 ，李 维 ，罗德安

（1.北京建筑大学测绘与城市空间信息学院，北京 102616；2.北京建筑大学北京未来城市设计高精尖创新中心，北京 100044）

在诸多建筑物的室内环境中，获得高精度的位置信息是一项具有挑战性的任务.由于卫星信号的衰减，传统方法（如GPS）在建筑物内部无法正常工作，这促进了室内定位系统的快速发展，例如基于WiFi[1]，ZigBee[2]和RFID[3]的室内定位系统.然而，当使用无线电技术来解决室内定位问题时，物理障碍物产生的影响无法避免，会对定位系统接收信号产生干扰.此外，上述提出的室内定位解决方案的另一个需要解决的问题是都需要部署特定设备或在定位过程中使用额外的硬件，并且基础设备需要定期维护，这些都需要高昂费用.

因此，无需额外设备投入的地磁定位技术备受关注.地磁场通常用于确定设备的航向[4].然而，室内环境中的重大磁扰动往往会对定向估计的准确性造成不利影响.通常需要校准，但这不是一件容易的事情.另一方面，建筑物中的混凝土与钢结构以及磁性铁质设备对室内地磁场造成的形变，可以被视为信息源.因此可以利用室内磁场的局部异常来获取室内各个位置的独特标记，采用类似“指纹”的方式构建参考图，而且室内地磁场在几周甚至几个月的时间尺度上具有稳定性[5-6].

早在2000年，Suksakulchai 等[7]认识到磁场干扰可以用于室内定位.在进行室内地磁定位时，需要已知的地磁参考图.虽然同时定位和建图（SLAM）技术克服了这个问题[8]，但大多数相关工作主要集中在解决匹配定位上，匹配算法通常是采用粒子滤波算法（particle filter，PF）.文献[8]结合智能手机中的惯性传感器，以航迹推算算法作为粒子滤波器的运动模型，利用测量磁场的总强度更新粒子权重，两条走廊之间的角落则被用作位置矫正的地标，同时对匹配区域的范围进行约束，在实验中实现了小于1 m 的定位精度.文献[9]中，利用现有的地磁参考图和地磁传感器的测量信息用粒子滤波器进行定位.实验表明，相比于只用磁场总强度，若同时考虑磁场的3 个分量会使得定位精度更高，在小区域的室内定位中可以达到厘米级.文献[10]提出了一种在粒子滤波器的实现中使用惯性传感器并应用磁场图和室内地图的方法，以提高定位和跟踪的准确性；使用梯度下降法来纠正由于磁扰动引起的用户航向估计问题；使用磁场三分量加室内地图的实验实现了0.75 m的平均定位精度，标准偏差为0.52 m.

现有基于粒子滤波算法的室内地磁定位中大多是以点为匹配单元，基于点的匹配模式一共有3 种组合（磁场强度；水平分量和垂直分量；x、y、z轴分量），一个点的地磁匹配特征最多只有3 个.如果只依靠磁场测量值，在地磁匹配中会导致定位结果模棱两可[11].增加匹配特征的数量是一个解决方法，因此本文提出基于路径的匹配模式，由多点构成的路径具有足够的匹配特征数量，文献[12]已经提出在一维路线中采用DTW （dynamic time warp）进行路径匹配，精度接近1 m.本文提出的匹配算法结合了DTW 与PF，构造基于路径的二维匹配模式，与一般的基于点匹配的模式相比，在匹配特征数量方面，具有更大的优势.同时通过计算地磁序列之间的相似度作为辅助定位手段.最后通过实验对本文提出的匹配方法进行评估.

1 地磁室内定位

地磁室内定位系统可分为离线构图与在线匹配两个阶段.离线构图是利用磁传感器遍历匹配区域，利用收集的地磁数据采用类似“指纹”的方法建立参考图；在线匹配是在目标运动阶段实时收集所在位置的地磁数据，并利用匹配算法将其与参考图进行最优匹配，得出目标的最佳估计位置，整个过程如图1.

1.1 粒子滤波（PF）算法

PF 算法是基于蒙特卡罗思想的一种最优贝叶斯估计，在分析非线性、非高斯的动态时变系统问题上具有突出优势.一般而言，后验概率分布p(xt|zt)十分复杂不容易获得，当系统的先验概率分布和似然函数已知时，粒子滤波器使用蒙特卡洛定位方法对其近似，原理就是利用粒子的状态作为先验概率，目标观测值作为参数与粒子所在位置对应的参考值做匹配，最后推导目标的最大似然估计.整个粒子滤波算法包括三个步骤：预测，更新和重采样.预测与更新方法如式（1）.

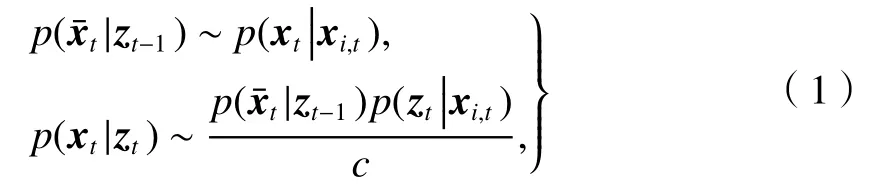
式中：xt为目标状态；为目标预测状态；xi,t为第i个粒子的粒子状态；zt为观测值；t为时间；c为归一化常数.

为了解决迭代过程中粒子衰减问题，粒子滤波器加入重采样（sampling importance resampling）算法.重采样的基本思想是去除权重小的粒子，并对权重大的粒子进行复制.在二维定位中，以行人运动轨迹为粒子滤波算法的运动模型，如式（2）.

式中：l～U(0,L)；L为目标移动步幅长度；

式中：设定行人当前所在位置的方向为初始值0，θ为行进过程中与初始方向之间的偏移量.

似然函数是基于单变量高斯概率密度函数，如式（4）.

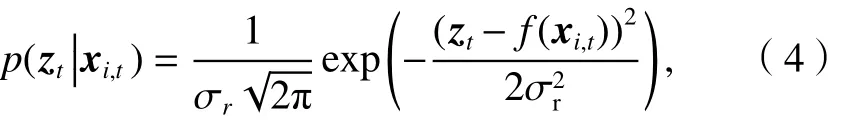
式中：σr为 观测值zt的协方差；函数f(·)返回粒子xi,t在参考图中对应的参考值.

式中：N为采样粒子个数；wi,t为时刻t第i个粒子的权重.

并且，定位误差定义为

1.2 动态时间规整算法（DTW）

在进行地磁路径匹配（地磁序列匹配）时，收集地磁数据的行走速度不同，可能会使得由于速度不同产生的两个序列的单个样本不准确.用DTW 进行比较的好处是能够允许两个序列在时间尺度上变化.DTW 算法通过实现两个序列之间的度量距离最小值，将一个序列的样本映射到另一个序列.算法定义的距离度量具有时间尺度上的不变性.地磁路径匹配是对室内两条不同路径上每个点的地磁强度进行对准，确定两条路径是否存在偏差，以及偏差的大小，这是室内地磁DTW 算法的概念.假设目标走过的路径为Q，长度为K=q，某个粒子走过的路径为P，长度为K=p.DTW 算法的度量距离定义为

式中：D(q,p)为长度分别为q、p的路径Q、P之间的度量距离；d(q,p)为路径中对应点的欧几里得距离，d(·)=‖·‖.

同时地磁序列之间的相似度可以作为辅助匹配手段，通过计算Spearman 相关系数确定相似度，该系数定义为

式中：xm、ym分别为两条序列中第m个数据；M为序列中数据总数；、分别为两条序列数据的平均值.

系数越高地磁序列相似度越高，并且该系数要求两条序列的长度要一致.

联合算法整体上还是遵循粒子滤波器的框架，整个联合算法的流程如图2.它与一般的粒子滤波器相比，优势在于：

图2 联合算法流程Fig.2 Process flow of the joint algorithm

（1）在目标运动一定时间段后进行匹配，进而增加了匹配元素的数量，提高了匹配精度.

（2）利用DTW 算法，通过计算粒子与目标的距离度量值代替粒子权重，无需重采样.

（3）减少了对粒子群数量的需求.

（4）利用地磁序列相似度来辅助定位.

2 实验数据采集及参考图构建

实验地点是北京建筑大学测绘学院二楼走廊，长68.0 m，宽1.8 m，平面图如图3（a）.本文采用“指纹”模式的方法，采集二楼走廊的地磁数据用于构建参考图（图3（b））.

图3 走廊平面图以及地磁参考图Fig.3 Corridor plan and geomagnetic reference map

为了能快速收集室内地磁数据，团队（城市测绘研究所）开发了一款测量机器人，上面搭载的地磁传感器HMC5983 装载位置距离地面1.3 m，能够避免机器人自身的影响，如图4[13].HMC5983 体积小，具有自动偏置补偿以及温度补偿功能，携带I2C 或者SPI 的数字接口，最大输出功率为220 Hz，航向角的精确度为1°～2°.

实验中，控制装有地磁传感器的测量机器人沿着走廊收集了4 行间隔0.6 cm 的地磁数据.机器人步长为0.2 m，每25 Hz 测量一次磁感应强度，产生三维矢量B=(Bx,By,Bz)，单位为μT，每个点采集时间10 s.为了进行定位，本文使用磁感应强度‖B‖作为匹配特征，计算方法如式（9）所示.因为磁感应强度是一个旋转不变量，避免了设备在运动过程中轻微抖动对实验的影响.

采集的参考地磁数据，利用克里金插值法进行处理，并且赋予网格坐标，构造的参考图如图3（b）.从图3中可知，受建筑物钢筋混凝土结构的影响，走廊地磁扰动随空间位置的改变而发生明显变化，因此能够用于室内定位.而图中红色圆圈则表示存在地磁强度相似现象，这导致了室内地磁特异性的减弱，同时给定位结果带来误差.

图4 测量机器人结构Fig.4 Structure of a measurement robot

3 实验结果与分析

本文首先通过实验分析在采样粒子分布相同的情况下N与K对定位精度的影响.使用测量机器人随机从某点（如点（1.2，15.4）m）开始沿着Y轴直线运动15 次，L设为0.6 m.在线采集地磁数据，获取15 个位置点，路径长度分为 1、2、···、14，如图5，图中所示相邻两个点位之间的路径长度为1.另外基于路径匹配只能从点2 开始，而且在每个位置进行匹配，所能使用的特征数量与点号的值相等.

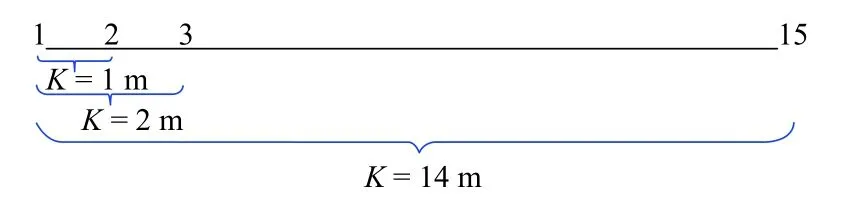
图5 点位与路径长度关系Fig.5 Relationship between points and path length

地磁数据采集完后，利用联合算法将它与地磁参考图进行匹配，其中粒子滤波算法中粒子分布的方式采用随机分布，匹配次数设定为300 次，联合算法通过MATLAB 计算机语言编写实现，平均定位误差与误差占比（误差e小于1 m）分别如图6、7 所示.

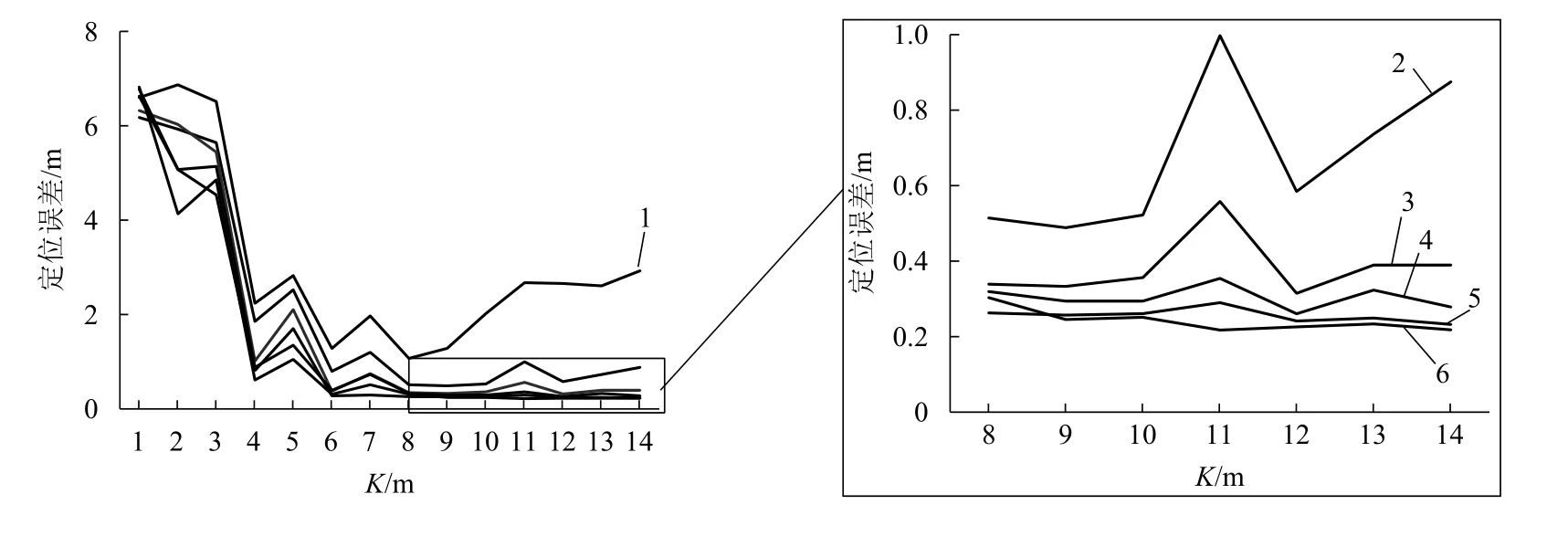
图6 不同粒子数随着路径增加的定位结果Fig.6 Positioning results of different particle numbers increasing with path

图7 误差占比（e ＜ 1 m）Fig.7 Proportion of error（e ＜ 1 m）

从图6可知，当粒子稀疏时会出现定位不稳定的情况，如N= 100 和N= 200，这与粒子的分布有关系.当N＜ 500 时，K= 5 m 和K= 7 m 出现波动情况，这与路径的选择有关，但不会影响实验的整体定位结果，后续实验会进一步说明.

充足的粒子数可以保证粒子分布密集，因此粒子随机分布在目标周围的概率增大，使误差小于1 m的定位结果出现的概率也增大，如图7.而且当粒子数一定，误差小于1 m 的百分比随着K的增加而提高；当N＞ 300 后，误差区百分比的变化趋势（随着K值推移）基本保持一致.

总而言之，当N＞ 100，整体的定位精度随着K增大而增加，尤其是当N＞ 300、K＞ 7 m 时，定位精度优于1 m.同时表1显示了不同粒子数对联合算法的影响，表示粒子数与匹配时间近似成正比.并且确定后期实验粒子数N= 400.

表1 不同粒子数匹配时间Tab.1 Time required to match different particle counts

传统粒子滤波定位结果如图8.从图8中能看出，采用粒子滤波对同一条路径进行单点定位的结果大致在点5 处开始收敛，但是收敛结果时好时坏，随机匹配20 次中，最大收敛误差能接近20 m，同样最小收敛误差也能小于1 m.在重复匹配300 次后，得出在第15 号点的各定位误差范围所占百分比情况，同时与本文提出的方法进行比较，如图9（a）.图中能充分说明在基于单点匹配的模式下，会导致粒子滤波器的稳定性下降，很显然这样的稳定性不足以用于室内定位，相比之下本文提出的方法具有良好的稳定性，1 m 以内的定位精度接近100%，但是匹配时间方面，如图9（b）所示，单点匹配所耗时间基本不变，且低于路径匹配.

图8 同一路径基于粒子滤波器单点定位结果（N = 400）Fig.8 Positioning results of single point for the same path based on particle filter （N = 400）

图9 粒子滤波器基于单点匹配和联合算法基于路径匹配的误差占比以及匹配时间Fig.9 Error ratio and matching time of the particle filter based on single point matching and joint algorithm based on path matching

本文提出的方法中还加入了序列相似度作为辅助手段，实验在计算DTW 算法后不能直接确定最优位置估计，只能通过平均计算位置估计较好的前几组来得出最终位置.因为DTW 算法定义的度量距离是指计算两条序列的地磁强度差异，使得D(q,p) 值小的粒子不一定靠近目标.而加入Spearman相关系数做为相似度辅助是为了让 ρ 与D(q,p) 进行互补.ρ 为序列间的梯度变化，当它取最大以及D(q,p) 取最小时就可以得出最优估计位置.为了验证辅助手段的有效性，取N= 400 分别进行匹配，结果如图10.从图10中可知，从K= 1 m 到K= 14 m，采用地磁序列相似度作为辅助手段都能够提高路径匹配过程的定位精度，路径长度小于4 m 效果最好，路径长度在4～8 m 之间其次.为了验证方法的鲁棒性，又随机从不同任意点开始收集4 条路径的地磁序列（一共5 条），移动步长不变.粒子数N设定为400，其中包括2 条直角转弯路径，结果如图11.图11中1、2、3 表示直线路径，4、5 表示包含直角转弯的路径，很明显当K＞ 9 m后，最优定位精度在1 m 以内，而且不存在定位误差突然剧增现象，说明本文所提出的算法性能可靠，具有良好的鲁棒性.另外本文实验是验证基于路径模式的室内地磁定位的可能性，同时得出该系统的定位精度，所以测量机器人的移动步长和航向角都属于人工控制.

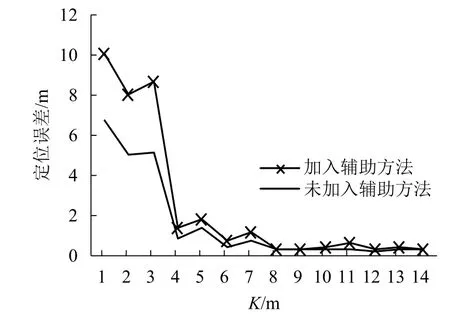
图10 定位结果对比（N = 400）Fig.10 Comparison of positioning results （N = 400）

图11 不同路径定位误差比较Fig.11 Comparison of positioning errors for different paths

4 结 论

在基于位置服务的发展中，室内定位是前提.各种定位方法中，基于地磁定位的方法因不需其他基础设施投入而受到广泛关注.然而在大型建筑中，地磁场的特异性会减弱，一般的基于粒子滤波器的定位方法会导致定位结果出现模糊现象.在本文中，提出了一种新的基于地磁的室内定位技术.该技术中有3 个创新点：（1）提出一种基于粒子滤波器与DTW的联合算法；（2）一种新的基于路径匹配的地磁定位模式；（3）使用地磁序列相似度进行辅助，后期实验也证明了辅助手段的有效性.最后实验证明，与传统的基于粒子滤波算法的室内地磁定位方法相比，该算法有效地解决了定位模糊问题，当路径长度和粒子数足够时（K≥ 9 m，N≥ 400），总体定位精度优于1 m，而且定位精度小于1 m 出现的概率接近100%，体现了该算法具有良好的稳定性与可靠性.