牵引式滑坡后缘破裂面计算方法
孙立娟 ,崔 凯 ,杨 涛 ,成启航
(1.西南交通大学土木工程学院,四川 成都 610031;2.西南交通大学高速铁路线路工程教育部重点实验室,四川成都 610031;3.西南交通大学交通隧道工程教育部重点实验室,四川 成都 610031)
自然斜坡在工程开挖或者河谷下切作用下,常会引发牵引式滑动破坏.首先发生局部滑动,在后缘产生拉裂缝,其上方坡体失去支撑,导致后缘后侧斜坡体变形失稳,并逐级向坡顶延伸,形成牵引式滑坡[1-3].如渝怀铁路DK615 + 602~ + 830 工程滑坡,即为施工开挖切坡形成的大型中层牵引式工程滑坡.滑坡内共发育3 级滑体,各级滑体后缘裂缝分别距线路中心为97、140 m 和220 m,同时,伴随有滑体下错和裂缝扩张等现象[4].
现场调查表明,在牵引式滑坡逐级失稳过程中,滑坡体各级滑体均有后缘拉裂缝,通常依据该裂缝判断滑坡周界和分布范围,但裂缝在滑坡体内部的空间形态以及如何延伸发展至潜在滑带难以探知.事实上,后缘破裂面的空间分布很大程度上决定了滑坡体的规模,对滑坡稳定性分析、滑坡推力计算以及牵引式滑坡的加固设计等方面均产生重要影响.目前,后缘破裂面在滑坡体内的空间位置尚无较好的确定方法,即后缘面的具体倾角难以精确量化.因此,开展牵引式滑坡后缘破裂面形成机制的理论研究具有重要意义.谭福林等[5]针对牵引式滑坡滑体间相互作用力学特征建立合理的物理和数学力学计算模型,初步推导牵引式滑坡推力计算公式.张俊瑞[6]采用传递系数法即有限元数值模拟对滑坡体在天然工况和暴雨工况下进行了稳定分析.宋东日等[7]提出了牵引式滑坡进行评价应坚持安全系数分区原则,滑坡总体加固应按安全系数控制,同时对后缘加固按位移控制.曹弼等[8]提出采用局部安全系数法,对不平衡推力法在牵引式滑坡的计算中进行优化.袁从华等[9]着重说明牵引式滑坡自下而上规模不断扩大的特性,提出了最初滑体采用有效加固、后牵引滑体采用加固补偿的原则等.
目前关于牵引式滑坡稳定性方面的研究,较少考虑后缘破裂面空间形态对坡体稳定性分析和滑坡推力计算等方面的影响.因此,本文基于工程实践中存在的问题,提出牵引式滑坡后缘破裂面的计算方法,确定出各级滑块的最危险破裂倾角,获得相邻滑块之间的条间力,并分段评价牵引式滑坡各级滑块的稳定性.同时,为验证理论方法的可行性,开展了室内模型试验,对后缘破裂面的形成机制进行深入研究和探讨.
1 后缘破裂面的理论计算方法
目前边坡稳定性分析常采用极限平衡条分法[10-18],这类方法难以准确考虑条块侧面的受力特性,熊将等[19]提出对滑体进行斜条分的极限平衡条分法.认为边坡滑动体必须碎裂成可以相对滑动的块体才能发生整体移动,同时条块底部和条块界面具有相同的安全系数,即滑体滑动时不但要克服主滑面的抗剪强度,还要克服滑体自身强度,该计算方法主要适用于岩质边坡.现场调查发现,发生牵引式破坏的土质边坡滑块间同样发生相对滑动,其破坏模式与岩质边坡节理构造特点相似.不同的是,岩质边坡的岩层产状以及节理倾向、倾角均为已知,可以直接用于稳定性分析.而牵引式滑坡的后缘拉裂面形态难以确定.因此,对Sarma 法进行改进,认为滑块界面和滑动面上的剪切强度具有不同折减系数,根据各级滑体的最危险破裂面来划分条块,初步推导牵引式滑坡后缘破裂面倾角的计算公式,并分块评价各级滑体稳定性.
1.1 牵引式滑坡计算模型
牵引式滑坡在逐级失稳过程中产生多级后缘拉裂缝,相邻滑块沿破裂面发生滑动,通常表现为下错滑移.根据牵引式滑坡演化机制建立合理的概化模型及划分简图,将牵引式滑坡共分为n级滑块,如图1和图2所示.

图1 牵引式滑坡概化模型Fig.1 Retrogressive landslide generalisation model

图2 滑块划分及编号简图Fig.2 Sketch of slice and block number
1.2 后缘破裂面倾角的计算原理
牵引式滑坡具有逐级向后发展的特性,滑坡体内通常发育多级滑块.初始时,第1 级滑块处于稳定状态,由于地表水渗入或地下水上升等原因,导致滑面抗剪强度降低,逐渐进入极限平衡状态,此时滑块土体抗剪强度发挥作用,承担了一部分剪切力,破坏继续发展,直至后缘面逐渐贯通至滑面,滑块抗剪强度完全发挥出来,滑块失稳.因此,假定滑带土抗剪强度降低到一定值后,既有滑面出现失稳滑动,继而在滑块中形成拉剪破坏面.此时,仅计算既有滑面的安全系数,破裂面在原抗剪强度参数下处于临界状态.由于土体抗拉强度极低,故计算时不计黏聚力的影响,求得各级滑块安全系数最小时对应的后缘面倾角,即为滑体破裂面倾角.
图3为牵引式滑坡体计算模型.图3中:Wi为第i级滑块单元的重力,i=2,3,···,n;Ni为 作用在第i级滑块单元滑动面的正压力;Ti为 作用在第i级滑块单元滑动面的剪切力;Ei-1、Ei分别为作用在第i级滑块单元左、右侧面上的正压力;Xi-1、Xi分别为作用在第i级滑块单元左、右侧面上的剪切力;li为第i级滑块单元的滑动面长度;Li为 第i级滑块单元的后缘破裂面长度;αi为 第i级滑块单元的底滑面倾角;θi-1、 θi为第i-1、i级滑块单元的后缘破裂面倾角.在该计算模型中,根据滑块极限平衡条件和破裂面的莫尔-库伦强度破坏准则,建立任意第i级滑块单元的平衡方程.

图3 牵引式滑坡体计算模型Fig.3 Sliding-block computation model of retrogressive landslide
设滑块i具有稳定性系数Fi,则底滑面BiB1满足极限平衡条件:

底滑面失稳滑动后,后缘破裂面B1C1形成,B1C1为拉剪破坏面(因拉破坏产生的裂缝深度较小,此处忽略不计),则有

式(1)~(2)中:czi为 第i级滑块单元底滑面的粘聚力;φzi为 第i级 滑块单元底滑面的内摩擦角;cmi为第i级滑块单元后缘破裂面的粘聚力;φmi为 第i级滑块单元后缘破裂面的内摩擦角.
极限状态下,滑块BB1C1满足静力平衡,水平方向的平衡方程为
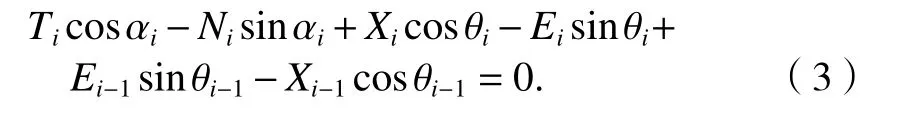
竖直方向的平衡方程为

将式(1)和式(2)代入式(3),消去剪力Ti和Xi,可得

将式(1)和式(2)代入式(4),消去剪力Ti和Xi,可得

由于滑块BB1C1处于极限平衡,则其同时满足力矩平衡,对B1点取矩,有
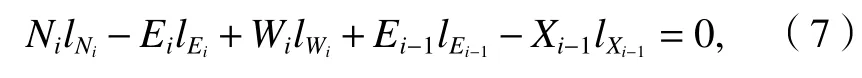
式 中:lEi、lNi和lWi分别为Ei、Ni、Wi对B1点的力臂;lEi-1和lXi-1分别为Ei-1和Xi-1对B1点的力臂,根据图3中几何关系确定.
联立式(5)、(6)、(7),求解安全系数Fi.安全系数Fi最小时,对应的后缘面破裂倾角θi即为所求.
为简化计算结果,令a=cosαi,b=cosθi,c=sinαi,d=sinθi,e=tanφzi,f=tanφmi,m=lAB1(模型中点A到点B1的距离),n=lB1C1(模型中点B1到点C1的距离).
采用Maple 软件解得第1 级滑块的安全系数

式(8)是假定后缘面破裂倾角θi条件下导出的.对于具体的滑坡体,应是使滑坡失稳段AB安全系数Fi最小时的θi.此时可将式(8)对θi求导,求得导数为0 时的θi,即为所求.但这会导致导数过于复杂,难以计算.为简单,本文假定若干θi(0~90°),根据滑坡模型获得相应的破裂面长度lBC、滑块面积Area及力臂lE1、lN1、lW1,代入式(8)求得安全系数F1,则最小安全系数对应的 θ1即为所求,同时,可求得剪切力T1和 法向力N1.在已知滑块1 和滑块2 条间力的条件下,按照上述方法,将各参数代入式(1)~(7),采用Maple 软件,计算第2 级滑块(条块2)的后缘面破裂倾角 θ2,牵引式滑坡其他滑块的计算方法与第2 级滑块相同.
1.3 实例验证
以文中牵引式滑坡室内试验模型为例详细说明上述方法的具体应用.模型几何尺寸如图4所示,其中滑带共分为4 段,分别为AB1段、B1B2段、B2B3段和B3B4段.

图4 试验模型计算简图(单位:m)Fig.4 Calculation sketch of the test model (unit:m)
第1 级滑块几何模型如图5所示,AB1为底滑面,长度lAB1= 0.384 8 m,倾角 α1= 6°,滑体土抗剪强度参数等效内摩擦角 φm1= 28.09°,滑带土抗剪强度参数等效内摩擦角 φz1= 18.56°,B1C1为后缘破裂面,长度为lB1C1,后缘面倾角为θ1.滑块AB1C1面积为Area,滑体土容重为13.74 kN/m3.为验证本文计算方法是否存在安全系数最小值,第1 级滑块后缘面破裂倾角θ1的搜索范围尽可能扩大.取滑带端点B1与B4的连线与水平面夹角作为搜索破裂倾角的最小值,取B1与坡面垂点的连线作为搜索范围的最大值,由此确定θ的搜索范围为30°~110°.
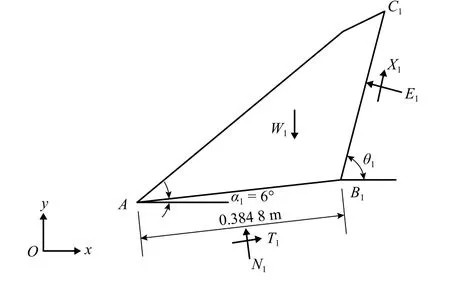
图5 滑块1 计算简图Fig.5 Calculation sketch of Block 1
将破裂面长度lB1C1、 滑块面积Area及力臂lE1、lN1、lW1,代入式(1)~(7),计算结果如表1所示,为形象表示安全系数与后缘面倾角的相关关系曲线,仅选取极值所在较小角度范围(50°~90°)进行表示.结果表明,滑块1 存在唯一最小安全系数0.877 9 (图6),与此对应的后缘面破裂倾角为71°,即第1 级滑块破裂倾角为71°.

表1 滑块1:后缘面破裂倾角计算结果Tab.1 Block 1: results of the fracture angle of the trailing edge
求得滑块1 法向力E1=0.288 9 kN,作用剪力X1=0.154 2 kN.
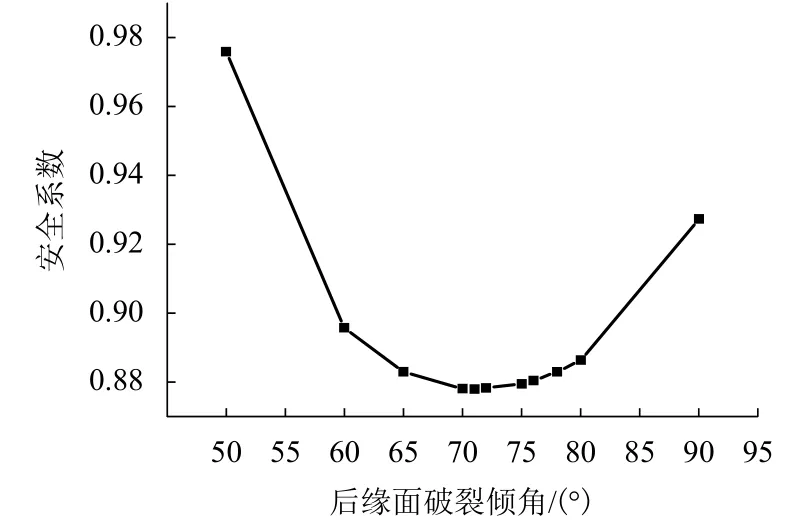
图6 滑块1 的安全系数曲线Fig.6 Safety factor curve of Blcok 1
第2 级滑块几何模型如图7所示,滑体和滑带计算参数与滑块1相同,仅滑带长度lB1B2、 α2和Area不同,将各参数代入式(1)~(7),计算结果如表2所示.后缘面破裂倾角θ2的搜索范围是滑带B1B2段末端与两滑块坡面分界点及坡面终端之间的角度范围,故θ的搜索范围为36°~122° 之间.为形象表示安全系数与后缘面倾角的相关关系曲线,仅选取极值所在角度范围(50°~90°)进行表示,如图8所示.结果显示,滑块2 的最小安全系数为1.050 4,与此对应的后缘面破裂倾角为71°,即第2 级滑块的最危险破裂倾角为71°.

图7 滑块2 计算简图Fig.7 Calculation sketch of block 2
求得滑块2 法向力E2=0.413 3 kN,作用剪力X2=0.220 6 kN.
第3 级滑块几何模型如图9所示,滑体和滑带计算参数与滑块1相同,仅滑带长度lB1B2、 α3和Area不同,将各参数代入式(1)~(7),计算结果如表3所示.取滑带端点B3与B4的连线与水平面夹角作为搜索破裂倾角的最小值,取B3与已确定的第2 级滑块后缘面坡顶点的连线作为搜索范围的最大值,搜索范围为39°~105° 之间,计算结果如表3所示,安全系数与后缘面倾角的相关关系曲线如图10所示.结果表明,滑块3 的最小安全系数为1.256 6,与此对应的后缘面破裂倾角为67°,即第3 级滑块的最危险破裂倾角为67°.

表2 滑块2:后缘面破裂倾角计算结果Tab.2 Block 2: results of the fracture angle of the trailing edge
采用上述计算方法,分别求得各滑块最危险破裂倾角θi,从前至后依次为71°、71° 和67°,对应的最小安全系数依次为0.878 0、1.050 4 和1.256 6.计算结果表明:各滑块均存在唯一最小安全系数,即各滑体存在唯一的最危险后缘面破裂倾角,且为小于90° 的陡倾角;滑块1 的安全系数最小,稳定性最差.本文的计算方法适用于具有既有滑面的老滑坡,且滑带为折线型或者直线型.为确定计算方法是否合理,开展了室内模型试验,验证计算方法的正确性和可行性.
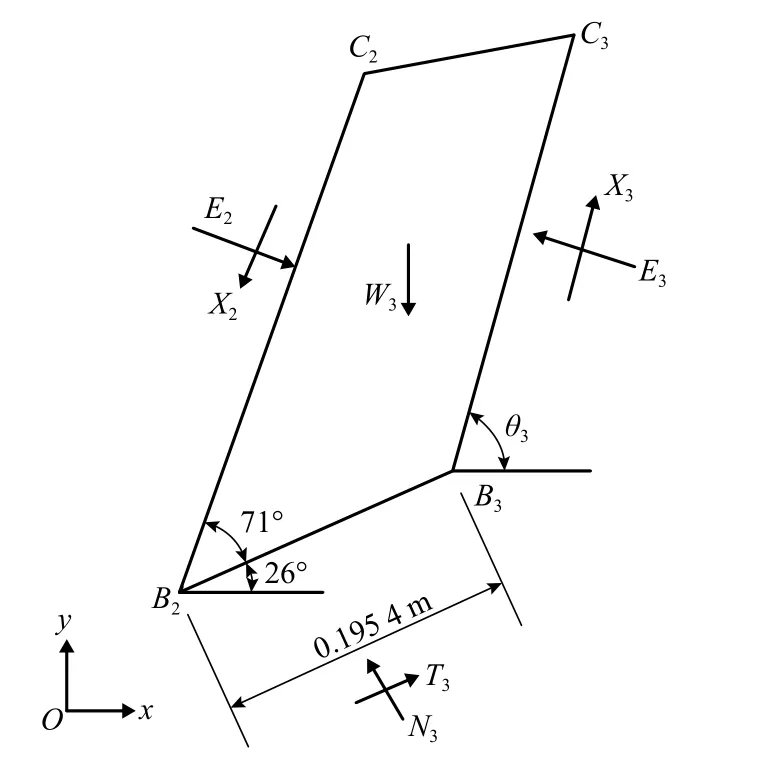
图9 滑块3 计算简图Fig.9 Calculation sketch of Block 3

表3 滑块3:后缘面破裂倾角计算结果Tab.3 Block 3: results of the fracture angle of the trailing edge

图10 滑块3 的安全系数曲线Fig.10 Safety factor curve of Blcok 3
2 模型试验
牵引式滑坡的致滑机理较为复杂,滑坡变形实质上是主滑带的生成、发育和变动的全过程.其中,地下水入侵或地表水渗入导致的岩土体逐渐弱化,抗剪强度降低是诱发滑坡的最主要原因.本文致力于研究牵引式滑坡变形失稳过程中的破裂面形态和破裂倾角特征研究,通过向渗透盒底面渗水,导致滑带土抗剪强度降低,来实现滑坡体的渐进破坏过程.
因此,提出了能够模拟地下水软化滑带的“分段式滑面底渗法”的模型试验方法,并研发了新型试验装置.通过分段注水软化滑带,实现牵引式滑坡逐级失稳,从而观测各级滑块后缘面破裂倾角的变化规律,并与理论计算结果进行对比,探讨牵引式滑坡后缘破裂面形成机制,为稳定性分析方法提供思路.
2.1 “分段式滑面底渗法”试验装置
目前,现有模型通常采用坡面降雨[20-23]的方式模拟牵引式滑坡的破坏过程”本文研发了“分段式滑面底渗法”模型试验装置,装置主体是由11 个渗透盒构成的分段式滑面,能够组成各种几何形状的滑动面.通过向不同分段滑带的渗透盒注水,使滑带局部软化失稳,模拟各种滑坡破坏模式.
渗透盒平面尺寸为30 cm × 12 cm,厚度为2 cm,制作材料是钢板,壁厚1 mm.渗透盒顶部盖板均布孔径为1 mm 的细孔,孔距1.5 mm.渗透盒内除下部安放支架外,保持空置,中部填充泡沫板和毛巾,从渗透盒底部引出注水管.从注水管外端注入设计水量,经泡沫板和毛巾的分解作用,从顶部细孔均匀渗出.从渗透盒底部引出注水管,将各组注水管设置为同一水头,与注水容器相连.同时,在注水管上部安装控水球阀,用于控制水的开启、闭合以及调节流速等.由于模型较小,为避免水分对滑体土的潜蚀作用,将注水速率控制在5 mL/min 左右.坡体材料渗透系数为3×10-5~5 × 10-5m/s,可以吸收全部渗入水量.同时,在渗透盒组成的分段式滑面上部依次填筑滑带土和滑体土.随着渗透盒内水分不断渗出,滑带土含水量不断提高,抗剪强度持续降低,最终导致滑坡失稳下滑.
2.2 试验方案设计
模型箱几何尺寸为120 cm × 30 cm × 80 cm.滑体土和滑带土均采用60 目石英砂和山东潍坊膨润土为原材料进行配置.滑体土和滑带土的砂土比均为2∶1.滑体土含水量按10%配置,滑带土含水量按20%配置.渗透盒编号从剪出口开始,向坡顶逐渐增大,编号依次为1、2、 3 、···、11.试验时,自渗透盒2 号开始,分段设置渗透盒的注水范围,模拟牵引式滑坡的逐级失稳过程.因考虑到坡体前端注水,易导致滑带底面冲刷产生流通孔洞,影响试验效果,因此渗透盒1 号并未注水.
分3 阶段设计工况,工况1 为渗透盒2 号、3 号和4 号组成的第1 级滑带,工况2 为渗透盒5 号、6 号和7 号组成的第2 级滑带,工况3 为渗透盒8 号和9 号组成的第3 级滑带.试验时,按序逐级软化滑带,观测各级滑块的后缘破裂面倾角.
2.3 试验过程与结果分析
试验主要目的是通过模拟牵引式滑坡渐进破坏过程,研究各级滑块后缘面倾角变化规律.试验原理是通过向底滑带注水,水分逐渐渗透至滑带土中,导致滑带土含水率逐渐增加,抗剪强度逐渐降低,继而引发滑块失稳.因此,首先需要确定出各级滑带所需的注入水量,即通过对滑带土进行抗剪强度测试,得出能够使滑带土强度衰减至零时的注入水量,以达到使滑块失稳的目的.因此需要绘制滑带土抗剪强度随含水率的变化趋势曲线,据此确定各级滑带的注入水量.图11为滑带土的粘聚力和内摩擦角随含水率的变化曲线.
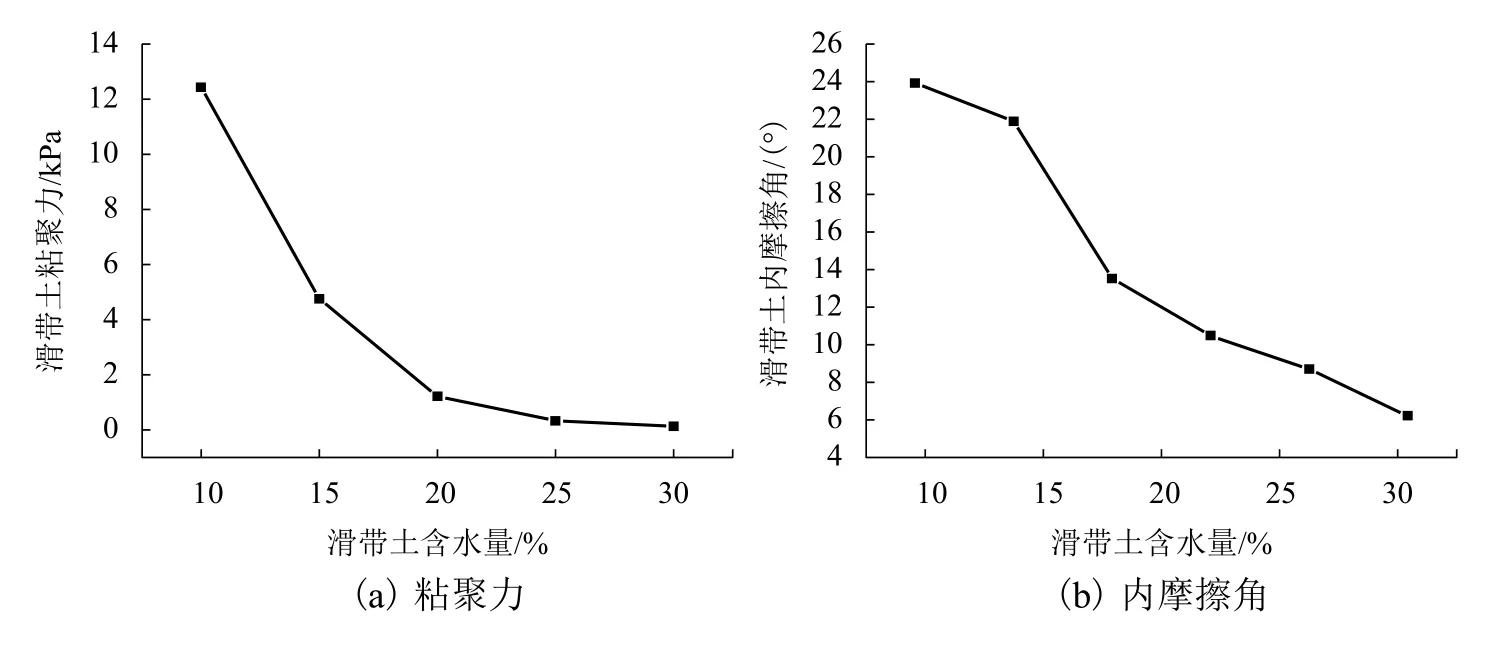
图11 后缘拉裂缝形态Fig.11 Morphology of tension crack of trailing edge
滑带土测试结果表明,滑带土的粘聚力和内摩擦角随含水量的增加而显著降低.含水率由10%增加至25%时,粘聚力基本衰减至0,内摩擦角降低至原来的60%.据此,向滑带土匀速注入设计水量,实现牵引式滑坡的逐级衰减过程.
首先向第1 级滑带(渗透盒编号2 + 3 + 4)缓慢注水,如图12,各渗透盒分别注水至200 mL 时,坡体开始有裂缝产生.考虑到水管较长,损耗较大,故首次注水量增加200 mL.持续注水,坡体变形继续发展,裂缝张开,坡体缓慢前移,累计注水至400 mL时,土体变形稳定,裂缝C1 位于滑带6 上方坡面处.静置待坡体稳定后,继续向第2 级滑带(5 + 6 + 7)持续注水至400 mL,裂缝C2 逐渐贯通,位于滑带8 坡面位置处,此时裂缝C1 逐渐变窄至消失,表示坡体发生向前滑移.最后向第3 级滑带(8 + 9)注水,与前面两级滑块相似,裂缝C3 位于滑带11 上方坡面处,此时C1 闭合,C2 逐渐变窄.本试验通过分级软化滑带,导致滑带土抗剪强度降低,后缘面逐渐贯通至滑带,引发滑坡体分级失稳.
上述试验过程详细表述了牵引式滑坡逐级失稳的渐进破坏过程.随着各级滑带强度弱化,分级滑块逐渐形成,失稳滑带与坡面裂缝表现出良好的相关关系.试验前坡体模型如图12(a)所示.为进一步明确后缘破裂面的空间形态特征,用后缘面破裂倾角θ来表示,定义为坡体后缘破裂面与已失稳滑带末端连线后与水平面的夹角,如图12(b)所示;第1 级滑带失稳,对应的后缘拉裂缝C1 如图12(c)所示;第2 级滑带失稳,对应的后缘拉裂缝C2 如图12(d)所示;第3 级滑带失稳,对应的后缘拉裂缝C3 如图12(e)所示;试验结束后,滑坡体变形形态如图12(f)所示.因第1 级滑带失稳引发的的坡体破坏范围称为第1 级滑块,其他类似.

图12 后缘面破裂倾角结果对比Fig.12 Comparison results of the inclination of the trailing edge
通过试验观测,得出各级滑块的后缘面破裂倾角如表4所示.

表4 后缘面破裂倾角统计表Tab.4 Inclinations of the trailing edge
根据试验现象和观测结果,可以发现滑坡体有如下变化规律:
(1)不同失稳滑带段仅观测到一条变形较大的裂缝,形同于滑坡体主裂缝,并向被软化滑带末端延伸,坡面裂缝沿边坡走向近似平行方向分布.受模型尺寸影响,次级裂缝发育不明显.
(2)后缘面破裂倾角均小于90°,即裂缝倾向均指向临空面.
(3)第1 级滑块稳定程度较低,变形最为显著.在滑坡体逐级失稳过程中,出现裂缝张开和滑体下错等现象.
2.4 理论计算与模型试验结果对比
将理论计算和模型试验结果进行对比,结果如图13所示.

图13 后缘面破裂倾角结果对比Fig.13 Comparison results of the inclination of the trailing edge
对比可知,后缘破裂面倾角计算值与试验值具有较高的一致性,主要出现在70° 左右,相对误差介于2%~4%之间.由于试验模型尺寸较小,受到尺寸效应和边界效应影响,导致一定程度的误差.
通过理论计算和试验结果可知,各级滑块均存在唯一的后缘破裂面倾角,该倾角所在面为滑坡体变形失稳时的最可能通过面.第1 级滑块的稳定程度最差,越向后侧滑块稳定性越好,原因是前侧滑块起到阻滑的作用.
由于土体中随机存在多种滑裂面形态,难以统一为某种固定形式.为了便于计算分析,文中将拉裂面简化成直线,而实际滑坡中观测到多为折线型或者弧线型.本文均简化为直线型,作为最不利情况考虑,后缘面的形成机理还需要做进一步的理论分析.
3 结 论
本文通过理论计算和模型试验相结合的手段,研究牵引式滑坡渐进破坏过程中后缘面破裂倾角的形成机理,得出以下结论:
(1)提出将后缘破裂面作为极限平衡条分法的条分型式,推导出后缘破裂面倾角的计算公式,获得相邻滑体之间的条间力,据此分段评价各级滑块的稳定性.
(2)理论计算原理是假设滑带土抗剪强度降低到一定值后,既有滑面出现失稳滑动,继而在滑体中形成剪切破坏面.此时,仅计算既有滑面的安全系数,破裂面在原抗剪强度参数下处于临界状态.
(3)研发了能够模拟牵引式滑坡渐进破坏过程的“分段式滑面底渗法”试验装置,由若干渗透盒构成分段式滑面,能够组成各种几何形态的滑动面,模拟各种滑坡破坏模式.分三阶段设计滑坡工况,通过向不同分段的渗透盒注水,可使滑带分段软化,土体抗剪强度不断降低,模拟牵引式滑坡的失稳过程,观测各级滑块的后缘面破裂倾角.
(4)后缘面倾角计算值与试验值具有较高的一致性,主要集中在70°左右,相对误差介于2%~4%之间.滑坡体失稳形成的各级滑块稳定性不同,第1 级滑块的稳定程度最差,越向坡体后侧稳定性越好.

