基于EEMD-Hilbert和FWA-SVM的滚动轴承故障诊断方法

张 敏 ，蔡振宇 ，包珊珊

（1.西南交通大学机械工程学院，四川 成都 610031；2.西南交通大学轨道交通运维技术与装备四川省重点实验室，四川 成都 610031）

滚动轴承广泛存在于机械结构中，作为重要的旋转结构，是最容易出现故障的部件之一.滚动轴承振动信号具有非线性与非稳定的特性，单从时域或频域进行故障诊断较困难[1].于德介等[2]首次引入固有模态函数（intrinsic mode function，IMF）分量应用于机械故障诊断，本文简称模态函数，将M 距离函数和支持向量机（support vector machine，SVM）进行结合实现故障模式识别，但经验模态分解（empirical mode decomposition，EMD）[3]分解出具有原始信号特征的IMFS 容易出现模态混叠，掩盖原始信号的真实特征[4-5].Wu 和Huang 等[6]在EMD 的基础上改进提出集合经验模态分解（ensemble empirical mode decomposition，EEMD），引入高斯白噪声能够有效地避免模态混叠[7]，分解出的IMFS 具有完整信息，但IMF 所含信息有限，还需进一步处理.Hilbert 包络解调是一种运用广泛的信息解调技术，但在确定带通滤波参数时需要丰富的经验，限制了该技术的发展[8]，若直接在模态函数上进行Hilbert 变换则可避免带通滤波参数的确定.

多分类SVM 通过核参数将特征向量映射到高维空间实现分类，参数的确定影响整个分类效果.何青等[9]用果蝇优化算法优化SVM 参数，但测试集量少，大数据下还有待验证.烟花算法（firework algorithm，FWA）[10]是Tan 和Zhu 在2010年提出的一种新型进化算法，具有很强的优化求解能力，应用在优化SVM参数时比粒子群算法（particle swarm optimization，PSO）迭代时间快且更准确[11]，近年来逐渐受到研究者的关注.

本文提出利用EEMD 将原始数据分解成IMFS，再对IMF 进行Hilbert 变换，避免带通滤波参数的确定，同时可对模态函数进行信息解调分析；将模态函数及其变换后的解调信息进行统计特征提取并降维处理；最后采用新型烟花算法优化SVM 分类参数，代入数据实现快速、准确的故障诊断.

1 数据特征提取

1.1 集合经验模态分解

EEMD 是通过给目标信号加入一定幅值的高斯白噪声，利用白噪声频谱均衡分布的特点来均衡噪声，有效地解决了EMD 出现模态混叠的现象.适用于各种非线性和非稳定的信号处理，步骤如下：

步骤1随机生成均值 μ为0，标准差 σ为en的高斯白噪声nm(t)，t为时间，设定原始参数，m表示第m次分解，1 ≤m≤M，M表示EMD 分解次数.

步骤2将高斯白噪声nm(t)加入待处理的信号y(t)中 ，得到信号为ym(t)，t为时间，即

步骤3对处理后的信号ym(t)进行EMD 分解，得到S个IMF 分量cs,m(t)，

式中：rm(t)为 第m次分解得到的余项；cs,m(t)为进行第m次EMD 分解后的第s个IMF 分量，由频率从高到低排列.

步骤4若m＜M，则返回执行步骤（2），M=m+1，到M次终止；

步骤5计算进行M次EMD 分解后得到每个IMF 分量的均值，根据不相关随机序列统计均值为0，消除加入高斯白噪声对真实IMF 分量的影响，即：

步骤6将(t)作为EEMD 最终得到的第s个IMF 分量.

1.2 Hilbert 包络解调原理

信号进行EEMD 分解得到排序降次的IMF，本文选取前几个作为研究对象，后面残存的以低频噪声为主，不予考虑.对选取的(t)进行Hilbert 变换，解调原理如下：

滤波器公式h(t)为

式中：δ(t)为脉冲函数.

解析信号公式q(t)为

1.3 统计特征提取与降维

将主要的IMF 及其对应的解调信息作为提取特征对象，为有效提取特征值，挑选最合适的统计特征值来对处理的信息进行特征提取，本文选取的统计特征值依次是均值、峰值、极差、标准差、偏度、峰度、变异系数和平方和.综合上述的所有统计特征量，特征维度较高，本文采用核主元分析（kernel principal component analysis，KPCA）对特征维度进行压缩提取，实现特征降维，便于后面快速故障诊断.由于篇幅问题，本文不对KPCA 降维具体内容进行论述，详细参考文献[12].

2 模式识别

2.1 支持向量机

支持向量机通过核函数来实现线性不可分向线性可分的转化，研究表明径向基核函数K(xi,yi)在SVM 中表现出良好的泛化能力[13]，将输入向量从原来的空间映射到高维特征空间P，并在该特征空间P内建立优化超平面.分类线方程为[14-15]

式中：(xi,yi)为 训练样本；ω为权值；x为输入向量值；b为阈值；l为向量的个数.

根据Karush-Kuhn-Tucker，优化各个系数得到最优决策函数为

式中：ai为Lagrange 系数.

最后得到适应度函数为

式中：C为惩罚参数；σ为核参数.

由式（10）可知进行SVM 分类模型构建时，性能的关键因素在于参数C和 σ的选取.

2.2 FWA-SVM 模型

FWA 是将每个烟花都当作一个解空间中的可行解，通过爆炸产生烟花点作为全局搜索的可行解.通过每个烟花的适应度值来变化爆炸半径和爆炸数，适应度值越小的点爆炸范围越小，爆炸数越多，适应度值大的则相反.烟花算法核心包括爆炸算子、变异操作、映射规则、选择策略4 个部分[16].

假定待求解的优化问题形式为minf(u)∈R,u∈Ω，Ω为可行解.烟花算法对SVM 参数优化步骤如下：

步骤1在解空间内随机生成N个初始un，有N个烟花；

步骤2计算每个烟花的适应度值与它们的爆炸半径Bn和爆炸花火个数Qn；

式中：ymin=min{f(un)},为这次迭代中的最优值，也为最小值，n=1,2,...,N；ymax=max{f(un)}为当前迭代中的最劣值，也为最大值；H为爆炸火花数的大小；ε为机器最小量，避免出现零操作.

为了避免适应度值优的或者劣的产生过多或者过少的爆炸火花，文献[10]对火花个数做出如下的限制：

式中：Sn为火花个数；a、b为常数.

步骤3产生爆炸火花，集合DC具有z个维度，z=round(D×rand(0,1))，D为烟花un的维数.在DC中的每个维度k下进行爆炸操作，再经过越界处理将Tnk保存到火花种群中.

式中：h为偏移量；unk为第n个烟花在第k维上的位置；Tnk为unk爆炸操作后的火花位置.

步骤4进行高斯变异操作，每个维度通过式（16）进行高斯变异，再经过越界处理保存到高斯种群当中.

式中：e～N(1,1)表示均值为1，方差为1 的高斯分布.

步骤5选择操作，在所有得到的种群中挑选最好的一个，另外N-1 个则通过轮盘赌法进行选择如式（17）、（18）.

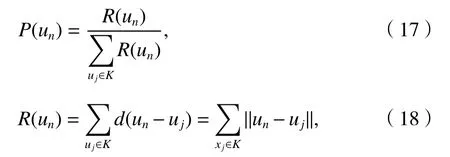
式中：P(un)为R(un)的 概率；R(un)为个体un与其它个体的距离之和；d(un-uj)是 指任意两个个体un和uj之间的欧式距离.

步骤6判断是否满足终止迭代条件，满足则结束输出最优SVM 参数，不满足就继续迭代.

2.3 基于EEMD-Hilbert 和FWA-SVM 的滚动轴承故障诊断

基于EEMD-Hilbert 特征提取和FWA-SVM 故障诊断具体步骤如下：

步骤1原始信号样本提取.获得设备运行所采集到的数据样本，对样本进行分组.

步骤2EEMD 分解处理.将样本数据进行EEMD 分解得到若干个IMF 函数.

步骤3Hilbert 变换处理.对选取的IMF 进行Hilbert 变换，获得瞬时频率.

步骤4统计特征提取.对IMF 分量和解调信息分别计算其对应的统计特征值.

步骤5KPCA 特征降维.提取出有用的信息特征实现特征降维.

步骤6FWA 寻SVM 最佳参数.将训练样本带入FWA-SVM 进行训练，得到最佳的SVM 分类参数.

步骤7模式识别.将训练好的FWA-SVM 模型进行测试集故障分类，输出结果.

基于EEMD-Hilbert 特征提取和FWA-SVM 故障诊断流程如图1所示.

图1 故障诊断流程Fig.1 Flowchart for troubleshooting

3 案例分析

为验证算法模型的可行性和有效性，本文采用美国Case Western Reserve University 电气工程实验室的滚动轴承实验平台数据[17]，实验中测试的轴承是由SFK 公司生产的6205-2RS 深沟球轴承.

3.1 数据特征样本

选取滚动轴承在转速为1797 r/min，采样频率为12 kHz 情况下的正常工作状态，内圈故障、滚动体故障和外圈故障3 种故障状态，其中外圈故障选择发生在6 点钟方向上.同时考虑3 种故障状态下的3 种损伤尺寸，分别为0.178、0.356、0.533 mm，具体数据如表1.

表1 轴承故障样本Tab.1 Bearing failure samples

将信号进行EEMD 分解，得到正常、内圈故障、滚动体故障和外圈故障，故障点直径为0.178 mm的4 个IMF 分量与其对应的原始信号如图2所示.

3.2 各种方法结果对比

3.2.1 不同信号处理方法的比较研究

方法a 将信号进行EEMD 和Hilbert 变换，通过统计特征量提取，再进行KPCA 降维，将特征数据代入PSO 优化SVM 参数模型内进行分类，记为EEMD_H模型.方法b 与方法a 类似，但不进行Hilbert 变换，记为EEMD 模型.方法c 对原始信号进行EMD 分解[18]，后面和方法a 一样，记为EMD_H 模型.PSO 初始参数为20 种群数，400 的最大迭代数.结果如表2（数据结果为5 次平均值）所示，图3是同一信号分别进行EEMD 和EMD 分解之后选择首个IMF 进行图像化的波形图.

进行EEMD 分解的迭代时间比进行EMD 分解时间更短，且正确率要低4%左右.图3说明EEMD可以较好避免EMD 的模态混叠现象.不加Hilbert变换处理的数据比加Hilbert 变换数据要差5%，说明加Hilbert 变换特征更全面，达到更好的数据特征提取.以上证明了EEMD_H 方法能够更精确地提取原始信号的特征信号，达到高效、准确的特征提取，证明了该特征提取方法的有效性与可行性.

3.2.2 算法参数寻优收敛性对比研究

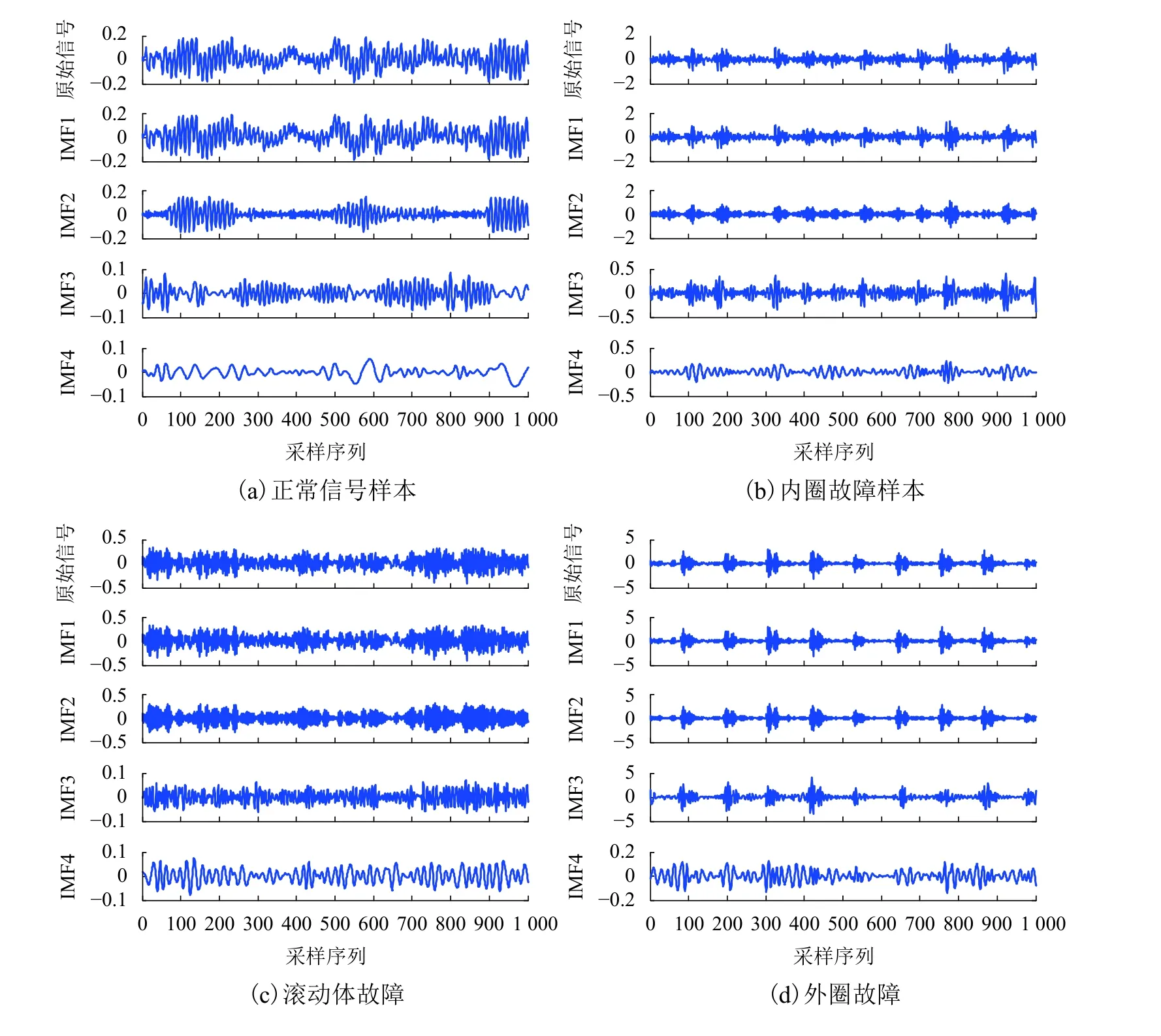
图2 原始信号和 IMF1～IMF4 分量波形图Fig.2 Original signal and IMF1- IMF4 component waveforms

表2 3 种分类结果Tab.2 Classification results for the three methods

利用目前成熟的粒子群算法和遗传算法（genetic algorithm，GA）优化SVM 参数构造的模型与烟花算法优化参数进行对比，所选的粒子群算法和遗传初始参数种群数为20，最大迭代数为200；烟花算法初始参数烟花种群数量为20，最大迭代数为200.结果如表3和图4所示，其中适应度值是原始算法中适应度实值的绝对值.

由表3与图4可知，FWA 优化SVM 参数比PSO更早达到最大值，且FWA 比PSO、GA 得到的训练集正确率更高，说明烟花算法比PSO、GA 在搜索域内能快速、准确得到最优的核函数参数.GA 算法源于搜索域较广，容易陷入局部最优，间接说明FWA的迭代收敛能力更强.另外FWA 与PSO 出现此类差别原因需从算法构造思路不同处进行分析：（1）烟花算法通过分布式信息共享，根据分布在不同区域烟花的适应度值决定爆炸强度大小和辐射范围，但PSO 是单项流动，搜索迭代过程是跟随当代最优解；（2）烟花算法中的高斯变异在变异中选出的不同维，而维度上的位移是相同的，保证了某些维度之间一些联系，而PSO 中各维变异是不相同的；（3）烟花算法中的高斯变异每代都要进行，而粒子群中每隔一定的迭代次数才运行1 次.

3.2.3 不同模型的故障诊断效果对比研究

利用遗传算法GA 和粒子群算法PSO 分别优化SVM 参数构造的模型与烟花算法FWA 优化SVM 参数进行对比，分别记为GA 模型、PSO 模型和FWA 模型.各算法初始种群数都为20，最大迭代数为400，其他都选各自最合适的参数.将上述处理好的训练集和测试集代入构造好的模型，进行结果分析.结果如表4（数据结果为5 次平均值）和图5所示.

从表4和图5可以看出，在时间上FWA 优化SVM 参数的平均时间只要14 s，相对较好迭代时间效果GA 缩短了100 s 多，而PSO 迭代时间较长，效果较差；FWA 优化的模型也在正确率上体现出优势，比GA 高0.4%，比PSO 高0.2%.以上说明FWA能够实现快速、准确地对SVM 参数优化，因此验证了烟花算法能够很好地优化SVM 参数，构建的模式识别模型能准确地进行故障诊断.

图3 两种方法首个IMFFig.3 Two methods for the first IMF chart

表3 FWA、PSO、GA 对SVM 参数寻优Tab.3 FWA，PSO，and GA for SVM parameter optimisation

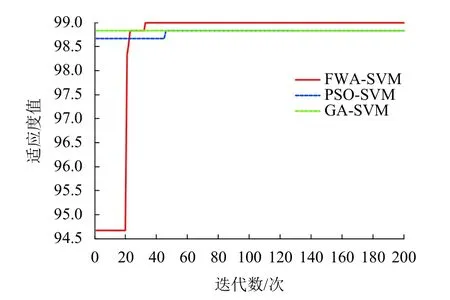
图4 3 种算法SVM 参数迭代对比Fig.4 Comparison of SVM parameters for the three algorithms

表4 3 种分类结果Tab.4 Classification results for the three algorithms

图5 3 种分类结果对比Fig.5 Comparison of the three classification results

4 结束语

提出一种采用集合经验模态分解、Hilbert 变换的特征提取方法，并利用烟花算法优化支持向量机分类参数的滚动轴承故障诊断方法.将振动信号进行EEMD 分解，避免了EMD 分解的模态混叠现象，准确提取信号特征；通过对IMF 分量进行Hilbert 变换获得频域统计特征，综合了Hilbert 处理数据的优点，避免带通滤波参数的选取，实现原始信号特征更准确提取；最后利用烟花算法优化SVM 参数，比传统的遗传算法、粒子群算法识别率更高，迭代时间更少，实现了快速、准确的故障诊断.案例分析的结果证明，运用该算法模型在故障诊断方面是一条可行的途径.