电动汽车充电接入点不同对电能计量影响

王兴贵，李 项，高敬更，郭 群

（兰州理工大学 电气工程与信息工程学院，兰州730050）

随着新能源汽车数量的快速增长，其充电设施的推广使用显得尤为重要。我国的电动汽车充电网络大多是通过10 kV/0．4 kV 变压器以三相四线制向用户供电。电动汽车作为单相负载接入充电网络时，因其充电行为的随机性和灵活性，不可避免地引起充电网络三相电流不平衡、有功功率线损高、电能计量异常等一系列问题，传统的电能计量方式无法精确计量。

为了保障电动汽车与其充电设施的推广使用，必须保证充电过程电量结算的准确、公平。当其接入充电网络进行充电时，由于充电接入点选择不同，因此带来的充电网络线路损耗与三相负荷不平衡度也不同。在三相负荷不对称时，由于实际的充电网络采用三相四线制供电，中线上存在阻抗且不为零。此时电动汽车充电站使用三相单表计量每相用户负荷，并依据每相单表计量值来对每相用户进行收费是不合理的，存在计量误差。计量误差的大小与充电网络的中线阻抗和电流有关，其值越大误差越大[1-2]。

目前，关于电动汽车作为单相负荷随机接入充电网络，引起的三相电流不平衡造成计量失准、不同接入点网损不同等问题研究较少。在电力市场条件下，为保证公平、公正、公开地给使用者和电能生产者提供优质服务，建立现代化的电动汽车电能计量、管理和交易系统至关重要[3]。使其在保证电能计量准确、公平的前提下最大限度地降低充电网络运行线损，提高充电网络运行经济性。

本文采用多目标粒子群算法[4]对电动汽车随机接入充电网络所引起的三相不平衡和线路损耗问题进行优化。并根据所求得的最优解集，利用充电管理平台引导其有序充电。最终达到电能准确计量的同时降低充电网络的线路损耗，实现供电企业和电动汽车用户之间的双赢。

1 电动汽车充电介绍

1.1 电动汽车充电模式

我国电动汽车的主要类型为公交车、出租车、公务车、私家车等。充电模式分为慢速充电、常规充电、快速充电，其中慢速充电和常规充电为交流充电，快速充电为直流充电。在常规充电中又分为单相220 V 交流充电和三相380 V 交流充电，其适用的场所为商场、停车场等[5]。电动汽车充电方式又分为恒流充电和恒压充电2 种。本文主要研究常规充电中单相220 V 交流恒流充电的情况。

1.2 电动汽车充电站典型布局

根据目前电动汽车常规充电站规模的数据资料，一般以20～40 个充电桩来配置一个充电站，这种配置是考虑充分利用晚间谷电进行充电。若在负荷高峰时也考虑充电，则一般以60～80 个充电桩来配置一个充电站，此时充电成本上升，增加高峰负荷[6]。电动汽车接入充电站示意图如图1所示。

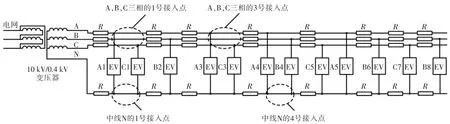
图1 电动汽车充电站示意图Fig.1 Schematic diagram of electric vehicle charging station

2 电动汽车充电接入点数学模型建立

电动汽车充电接入点优化问题包括多个目标，属于在一个探索空间上同时对多个目标进行探索的多目标优化问题。本文通过预测计算的方式确定电动汽车的最优接入点，使充电网络三相电流不平衡度最小的同时，最大限度地减小线路损耗。

由于电动汽车充电情况较为复杂，以图1 为例进行说明，电动汽车充电站经过10 kV/0．4 kV 变压器对三相四线制充电网络供电。现假设A，B，C 三相均设计有M 台均匀分布的单相220 V 交流恒流充电的常规充电桩（充电接入点）。为了方便建模，对充电桩进行编号。以A 相为例，对A 相的M 台充电桩进行编号并用矩阵表示为A=［1，2，3，…，M-1，M］，其中A 矩阵中的1 代表1 号充电桩，2 代表2 号充电桩，依次类推M 代表M 号充电桩。同理对B，C 两相充电桩进行编号可得：B=［1，2，3，…，M-1，M］，C=［1，2，3，…，M-1，M］，由图1 可知中线N 的编号矩阵为

式中：N 矩阵的第一、二、三行分别为A，B，C 三相的编号矩阵。有电动汽车接入的充电桩其编号矩阵对应位置数值变为1，未接入位置变为0。例如A，B，C三相的接入点分别为1，3，4，7；2，4，6，8；3，5，7，10。那么N 矩阵为

2.1 目标函数1：电动汽车充电网络三相电流不平衡度最小

电动汽车作为单相负荷随机接入充电网络，使得充电网络三相负荷不平衡，进而导致三相电流不平衡造成电能计量失准。值得指出的是在三相总负荷平衡，但三相负荷分布不平衡时，中线N 上存在电流，此时充电网络的三相电流仍是不平衡的。

根据GB/T 15543-2008 《电能质量三相电压不平衡》标准定义：三相电流不平衡度表达式为

式中：ξ1为三相电流不平衡度；IN为三相电流负序分量的均方根值；IP为三相电流正序分量的均方根值。但是此方法是建立在三相电流的相位和幅值均已知的情况下，而充电站三相电流的幅值和相位均在不断变化。鉴于此，本文采用一种较简便的方法求三相不平衡度[7]。

目标函数1 表达式如下：

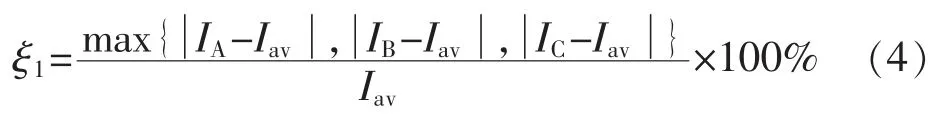
式（4）借鉴了电压不平衡度的计算方法，式中ξ1为三相电流不平衡度，IA，IB，IC为三相电流的有效值，Iav为三相电流有效值的平均值，单位为A，Iav=。

目前三相电流有效值的计算多采用均方根电流法和平均电流法，结合电动汽车充电站三相电流的实际情况，采用带权重的均方根电流法计算IA，IB，IC，其计算公式为

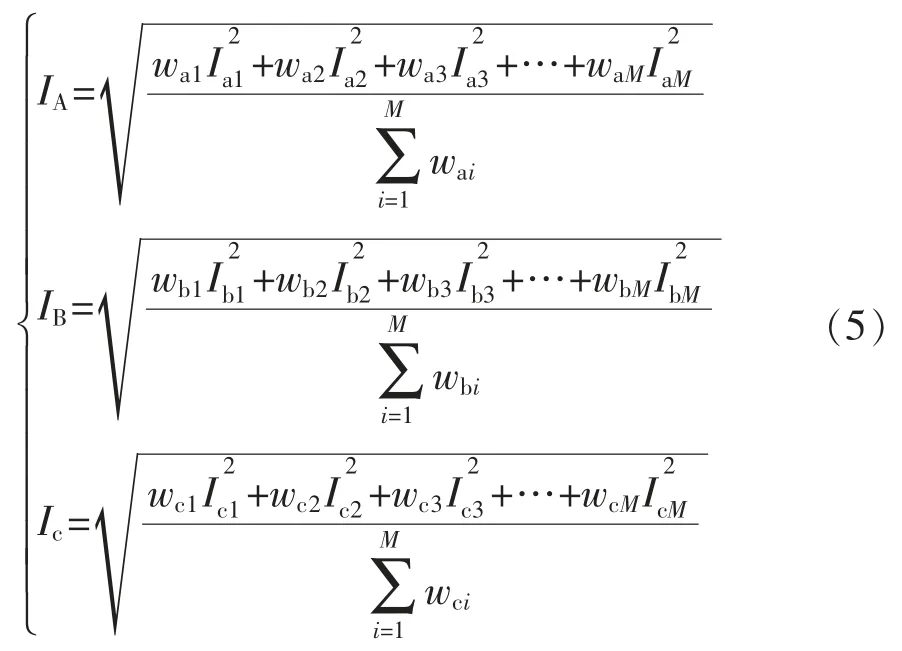
式中：wai，wbi，wci分别为A，B，C 三相中第i 号接入点电流的权重；Iai，Ibi，Ici分别为A，B，C 三相第i 号接入点的电流值，i=1，2，…，M。以A 相为例，假设A相某时刻只有第1，2，5，7 号充电桩有电动汽车接入进行充电，那么A 相电流的有效值IA表示为

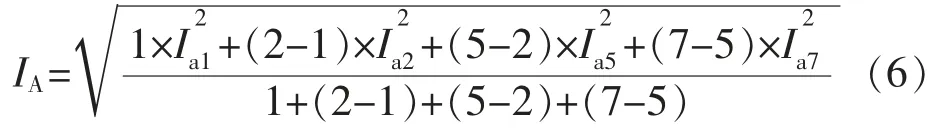
由式（6）可以看出wa1=1，wa2=1，wa5=3，wa7=2，其余没有电动汽车接入的充电点电流的权重均为0，有电动汽车接入的充电点电流权重wai与自身接入点该相前一辆电动汽车接入点位置有关。由图1 可知，A 相i 号接入点电流Iai为该接入点充电电流加上该相后面所有接入点充电电流之和，其他接入点依次类推。B，C 两相电流的有效值IB，IC的计算方法与A 相相同。

目标函数1 的约束条件：①充电网络任意接入点的电流值均不能超过电流允许的最大值；②电动汽车接入点只能是A，B，C 三相中某个充电桩。

约束条件如式（7）、式（8）所示：

式中：Iallow表示最大允许电流；INi表示第i 号接入点的中线电流值。

式中：EV 表示电动汽车的接入点位置矩阵。

2.2 目标函数2：电动汽车充电网络线路损耗最小

线损率是供电企业的一项重要经济技术指标，也是衡量其综合管理水平的重要标志。由于电动汽车充电行为的随机性和灵活性，当充电接入点选择不同时，充电网络线路损耗也随之发生改变。电动汽车充电网络为低压配电网，电压低，电晕损失和介质损耗均很小，一般可以忽略，因此线损主要为线路电阻的发热损耗。电阻热效应仅仅与电流和电阻的大小有关，而与电流的相位无关。对于三相四线制低压配电网线损计算问题，长期以来没有得到很好的解决[8]。本文针对电动汽车充电网络建立一种基于3/2 变换的线损精确计算模型。其线损包括A，B，C 三相和中线N 的线损。

目标函数2 的表达式如下：

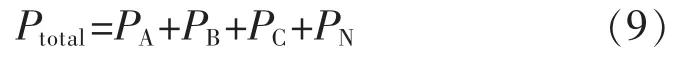
式中：Ptotal表示充电网络总的线路损耗；PA，PB，PC，PN分别表示A，B，C 三相和中线N 的线损。其中PA，PB，PC的计算如式（10）所示：

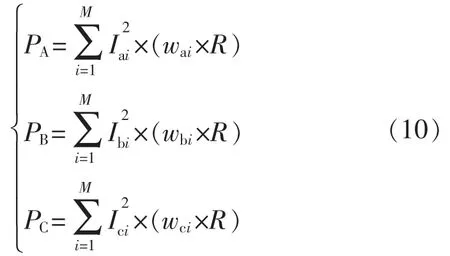
式中：R 表示同一相中两相邻充电桩之间的电阻；M为每相接入点的总个数。

对于PN的计算，与A，B，C 三相有所不同，中线电流INi不是第i 号接入点A，B，C 三相电流的算术相加，而是其相量和，其中i=1，2，…，M。鉴于此，将A，B，C 三相电流采用3/2 变换，变换到两相静止αβ坐标系下[9]。坐标变换为

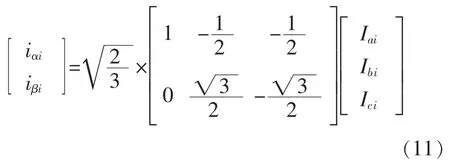
式中：iαi，iβi表示第i 号电动汽车接入点的三相电流在αβ 坐标系下的电流分量。将iαi，iβi合成即可得到中线电流INi，如式（12）所示：

此时PN计算方法与式（10）类似，如下式所示：

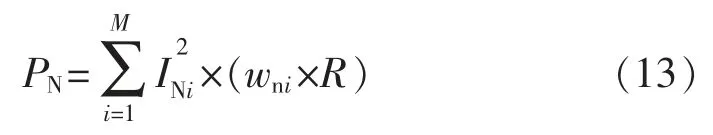
式中：wni的确定方式与wai，wbi，wci相同，R 表示中线两相邻充电桩之间的电阻。

根据电动汽车充电站典型布局，配4×70 mm2电缆、50 m 长，每5 m 设置一个充电桩，两相邻充电桩之间的电阻R 可由式（14）求得：

式中：ρ＝1．75×10-8Ω·m 为铜的电阻率；L=5 m 为相邻两充电桩之间的距离；S 为导体的横截面积70 mm2。经过计算求得R=1．25×10-3Ω。

目标函数2 的约束条件为

3 模型求解方法

电动汽车充电接入点的选择是一个非线性离散多目标优化问题，本文采用多目标粒子群算法（MOPSO）对模型进行求解。粒子群优化算法具有较好的鲁棒性和多样性且收敛速度快等特点[10]。此外，该算法还具有局部信息交互和全局信息交互的能力，在许多领域的单目标优化问题中表现优异。在单目标粒子群优化算法基础上Coello CAC 于2004年提出了多目标粒子群算法，进一步推动了粒子群算法的发展。将MOPSO 算法与电动汽车实际充电情况相结合后的流程如下：

第一步初始化种群POP，即确定电动汽车充电站的初始接入位置与接入数量；

第二步初始化每个粒子的速度，根据充电桩的实际情况，粒子速度只能以步长为1 进行寻优；

第三步评估种群POP 中每个粒子的适应度，即计算初始的三相电流不平衡度和线路损耗；

第四步在外部存储空间中存储代表非支配解粒子的位置信息，并初始化每个粒子的存储空间。即存储初始时刻充电网络的三相不平衡度和线路损耗；

第五步进行循环迭代寻找非支配解，即当有电动汽车请求接入时，将整个充电站中所有未接入的充电接入点作为搜索空间，评估其各个目标函数的适应度，并以初始的三相电流不平衡度和线路损耗作为标准进行筛选，将筛选所得解中的支配解剔除，剩余的非支配解存储到外部存储空间；

第六步当再次有电动汽车请求接入充电网络时，重复前面5 个步骤，循环往复最终实现电能准确计量的同时，使其充电网络线路损耗最小。

MOPSO 算法的流程如图2所示。

图2 MOPSO 算法流程Fig.2 Flow chart of MOPSO algorithm

4 算例分析

假设电动汽车充电网络中A，B，C 三相均设计有10 台均匀分布的单相220 V 交流恒流充电的常规充电桩，恒流充电桩的充电电流额定值为30 A，且每台充电桩同一时刻只允许一辆电动汽车接入进行充电。对于进行单相220 V 常规充电的电动汽车用户而言，可以选择接入A，B，C 三相中任意一台未被占用的常规充电桩进行充电。

在MOPSO 算法中用randperm 指令产生12 个1～30 以内不重复的整数并对其排序，将10 以内的数赋值给A 矩阵，代表A 相相应充电桩有电动汽车接入；将产生的11～20 的数均减去10 后赋值给B矩阵，代表B 相相应充电桩有电动汽车接入；将21～30 的数均减去20 后赋值给C 矩阵，代表C 相相应充电桩有电动汽车接入，以此来表示12 辆电动汽车的随机接入点。此时当有电动汽车请求接入充电网络进行充电时，该电动汽车将只能在余下的18个未被接入充电点中进行选择。采用MOPSO 算法对包含目标函数1和目标函数2 的充电接入点选择问题进行优化，根据优化结果确定其最佳接入点。

当已有12 辆电动汽车随机接入进行充电，第13 辆电动汽车请求接入进行充电时。若其随机接入余下18 个充电接入点中的任意一个，那么它分别接入这18 个充电接入点后充电网络的三相电流不平衡度和线路损耗分布如图3所示。

图3 优化前三相不平衡度与线损分布Fig.3 Three-phase unbalance and line loss distribution before optimize

优化前三相不平衡度及线损结果如表1所示。

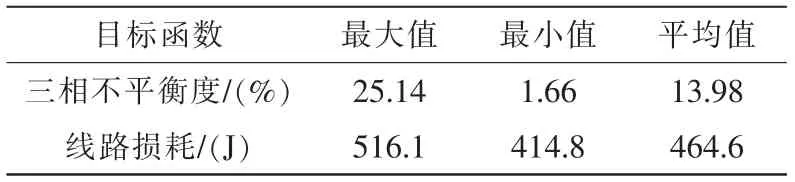
表1 优化前三相不平衡度与线损结果Tab.1 Results of three-phase unbalance and line loss distribution before optimize

采用MOPSO 算法对其进行优化后的三相电流不平衡度和线路损耗分布如图4所示。优化后三相不平衡度与线损结果如表2所示。

图4 优化后三相不平衡度与线损分布Fig.4 Three-phase unbalance and line loss distribution after optimize

表2 优化后三相不平衡度与线损结果Tab.2 Results of three-phase unbalance and line loss distribution after optimize

由表1和表2 可以看出优化前的平均三相不平衡度为13．98%，优化后为5．133%，降低了8．847%，有效地提高了电能计量的准确性。需要指出的是这仅仅是一次优化的结果，当不断有电动汽车请求接入充电网络时，采用本文所设计的优化算法对其持续优化，那么充电网络的三相不平度也将逐渐降低。最终维持在三相不平衡度允许的范围以内，实现电能的准确计量。

经济性分析：优化前平均线路损耗为464．6 J，优化后为429．2 J。优化前、后平均线路损耗的差为35．4 J，占优化前平均线损的百分比为7．62%，即可减少7．62%的线路损耗，降低了充电网络的经济运行成本。

由图4 可知经过MOPSO 算法优化后的非支配解不止一个且不存在绝对最优的充电接入点，为了使得优化结果更加直观明了，本算例选择三相不平衡度最小的点作为电动汽车充电接入点。并将该充电接入点用图形用户界面（GUI）进行显示，将所设计的优化程序植入电动汽车充电管理平台中，当电动汽车需要接入充电网络时，用户只需点击V2G1界面窗口中的“请求充电”按钮，在GUI 界面中将自动提示经过MOPSO 算法优化后的充电接入位置，用户将电动汽车接入该充电位置即可。充电接入点图形用户界面如图5所示。

5 结语

本文引入多目标粒子群优化算法，对电动汽车常规充电中因充电接入点不同而导致的三相电流不平衡度与线路损耗不同问题进行优化。对比充电网络优化前后的平均三相不平衡度和平均线路损耗可以看出，优化后平均三相不平衡度和平均线路损耗都得到了极大程度的降低。在提高电能计量准确性的同时，降低了充电网络的经济运行成本。通过算例验证了MOPSO 算法对电动汽车充电接入点选择问题优化的有效性。优化所求得的最优解集，可为供电企业制定电动汽车有序充电方案提供数据参考。

图5 充电接入点图形用户界面Fig.5 Graphical user interface of charging access point