改进的多模型粒子滤波弱小目标检测前跟踪方法

赵多禄，胡绩强

（兰州理工大学 电气工程与信息工程学院，兰州730050）

检测前跟踪方法主要应用于弱小目标的（信噪比低于10 dB）检测与跟踪[1]。检测前跟踪基本思路是通过雷达观测站收集的原始量测信息对目标的状态以及个数进行跟踪滤波。目前其主要的研究方法有2种：一种是分批处理方法，例如动态规划法[2]，Hough变换法[3]，这种方法的主要思路体现在每时刻累积多帧原始量测信息，其目的在于提高目标的信噪比，当目标的信噪比提高到一定的范围内，就可以将该目标当做点目标进行处理，这样可以选择很多方法进行实时跟踪处理；另一种是贝叶斯递推滤波方法[4-5]，例如粒子滤波（PF-TBD）实现弱小目标检测前跟踪的方法[6]，基于多模型粒子滤波实现弱小目标检测前跟踪方法（MMPF-TBD）[7]，然而当前MMPF-TBD 方法已经成为众多学者研究机动弱小目标的热点。MMPFTBD 充分地利用了粒子滤波能够实时在线的处理非线性、非高斯系统。但是当目标出现较强机动时，由于目标真实的加速度是恒定的，在递推滤波过程中致使前一时刻的模型与当前时刻的模型很难进行匹配，因此，使得粒子的传播偏离了真实目标的航迹，导致目标检测性能下降，严重时可能出现漏检情况。

针对上述问题，本文提出了一种改进的多模型粒子滤波弱小目标检测前跟踪方法。此方法的本质在于当目标出现较强的机动时，选取一个收敛的加速度运动模型来匹配目标的机动运动。这不但能够有效地避免目标的运动状态完全由模型状态转移矩阵与模型更新概率来控制，而且能够有效地提高目标模型的使用效率以及目标的检测概率。最终通过各模型滤波估计和输出目标状态[8]。

1 系统建模

1.1 运动过程建模

本文以2 种运动模型来描述目标的运动过程，并通过模型概率来控制2 种模型相互交替出现。其中一种是匀速直线运动模型；另一种是顺时针坐标转弯运动模型；假定两种运动模型的集合为s，其中s=｛1，2｝。则单个目标的运动方程为

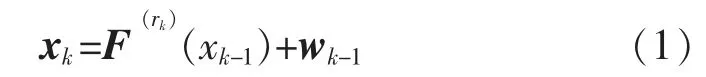
式中：T 为雷达传感器的扫描周期，且有

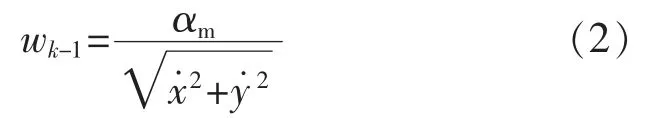
式中：αm＞0 是机动加速度。

当目标进行机动运动时，模型1和模型2 之间的交替运动服从马尔可夫转移矩阵Πm。

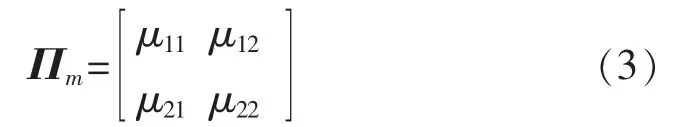
定义：φ1=P｛r1=1｝，φ2=P｛r2=1｝（满足φ1+φ2=1）为目标刚出现时分别按照两种模型初始运动的概率。用Ek∈｛0，1｝表示目标是否处于观测区域内，目标新生和死亡概率转移矩阵也为马尔科夫矩阵Πe[9]：

式中：Pb代表目标新生概率，Pd代表死亡概率。

1.2 量测建模

本文以目标的点扩展方式建立传感器的原始观测模型[10]。观测区的回波信号表示为距离-方位的观测数据，距离上有Nr个单元，方位上有Nb个单元，则每一帧观测数据由Nr×Nb个单元组成，对其中每一个分辨单元（i，j）对应Δx×Δy（i=1，…，Nr，j=1，…，Nb），这里我们假设各个分辨单元以及各个噪声之间相互独立。功率观测值可由下式建模：

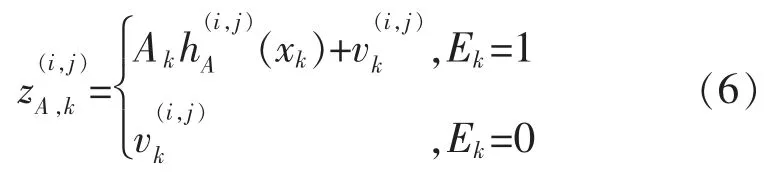
图1 为目标采用点扩展方式[11]建立的量测模型。幅值比较大的区域可能是目标的量测，而其他幅值相对较小的区域可能是噪声的量测。本文对于采用传感器点扩散函数形式，则在（xk，yk，zk）幅值强度参数Ak的目标对于分辨单元的强度贡献为

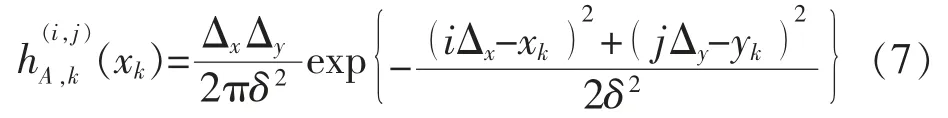
功率的观测值服从指数分布，μ0为指数分布的均值。

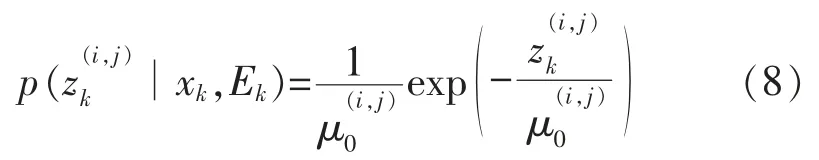
则可以推导出整个观测区域的联合似然函数为

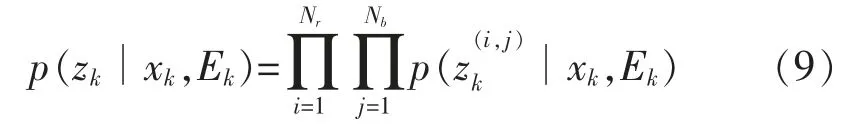
图1 采用点扩展方式采集的原始量测Fig.1 Original measurements using point expansion

2 IMMPF-TBD 实现过程

在MMPF-TBD 方法实现过程中，当目标出现较强的机动时，由于目标机动加速度αm为固定值，在滤波更新过程中目标前一时刻的模型与当前时刻的模型不能很好的匹配。IMMPF-TBD 利用一个固定的收敛函数来描述目标出现机动情况时目标的运动情况，目标机动过程分为若干区间段加以实现，也就是说当目标刚出现机动时目标的机动加速度比较小，逐渐的机动加速度变大直至达到最大。其它时刻目标做匀速直线运动时将机动加速度设置为0。通过这样的方法目标的运动模型能够实现更加精确的匹配。与此同时目标的检测性能会进一步的提高。

在原有的状态基础上进行扩维，将目标存在与否以及目标的模型信息以及加速度引入到新的混合状态，在此假设k-1 时刻目标状态的后验概率密度p（zk-1∣xk-1）可以用来表述，N 为整个过程采样粒子数。以下是IMMPFTBD 一次滤波递推过程：

第1步根据目标的运动模型以及目标的初始时刻的先验信息来确定目标加速度的分布f（αm），当目标在做匀速运动时，设定目标的加速度f（αm）=0，当目标出现机动时，目标按着f（αm）的分布情况，进行自适应的匹配目标的运动过程。

第2步根据前一时刻粒子的存在变量以及转换概率矩阵Πe来预测当前时刻粒子的存在变量，n=1，2，…，N。

第3步预测粒子状态，只对的粒子进行预测。这里分2 种情况对其进行处理：①对新生（即）粒子的预测。如果位置变量（xk，yk）处的能量幅值强度超过预设门限的分辨单元集，那么让这些粒子在此单元内服从均匀分布；②对存活的（即）粒子的预测。首先通过Πm和前一时刻该粒子的模型变量rk-1可以求取当前时刻的模型变量rk，然后根据rk对应的目标运动方程进行粒子状态预测。

第4步粒子权重计算，本文通过构造二元假设，即粒子似然比[12]的方法来实现整个粒子及权值的传递过程。

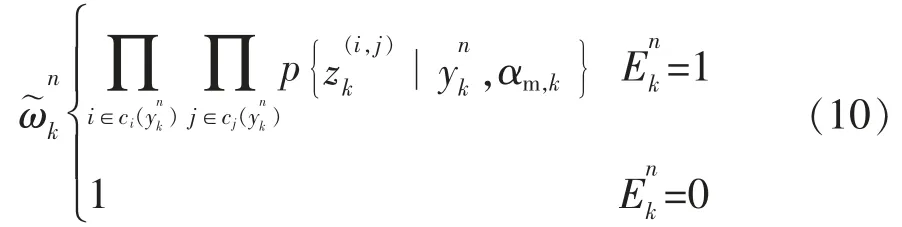
第5步粒子重采样→重采样样。

第6步目标状态估计，首先估计目标存在概率，即目标在该时刻采样得到的粒子数与采样粒子总数之比。

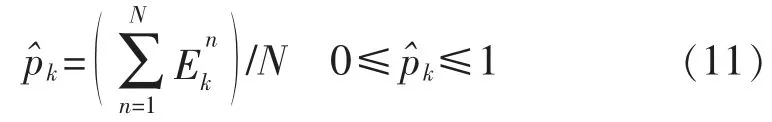
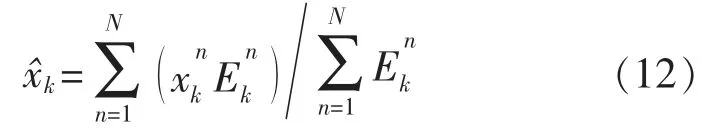
式中：R1，R2分别表示的数量。

3 实验仿真及分析

本次仿真传感器观测40 帧数据，其中目标在第7 帧出现，并且在7 帧～15 帧之间做匀速直线运动，15 帧～23 帧之间做协同转弯运动，24 帧～31 帧之间目标又做匀速直线运动。最后在第32 帧目标消失。

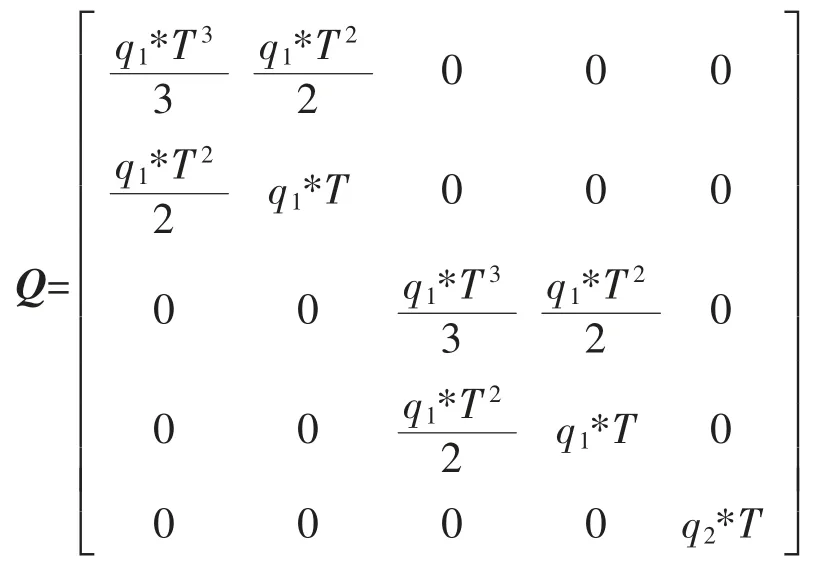
图2 是目标在SNR=3 dB 情况下一次Monte Carlo 仿真中对目标的跟踪过程，从仿真结果可以看出目标在强机动过程时刻，两种方法都能够实时的跟踪目标，这两种方法具有相似的跟踪效果。

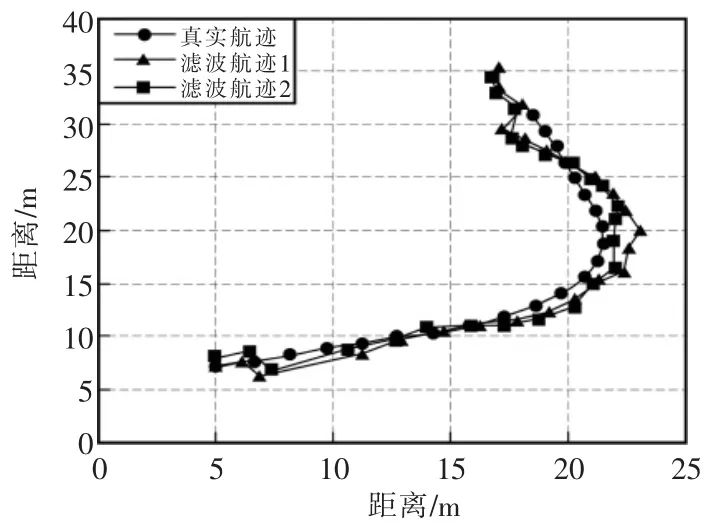
图2 两种方法的跟踪效果图Fig.2 Tracking effect diagram of two methods

图3 是验证IMMPF-TBD 方法在跟踪过程中的检测性能，从仿真结果可以清晰的看到当目标在进行匀速运动时，两种方法对目标都有较好的检测性能，都能够实时在线的检测到目标。但是，当目标发生机动时，MMPF-TBD 方法的检测性能严重下降，以至于出现漏检。相反IMMPF-TBD 方法能够较好的实时的检测目标。综合分析得出如下结论：当目标发生机动时刻，IMMPF-TBD 方法的检测性能优于MMPF-TBD 方法。

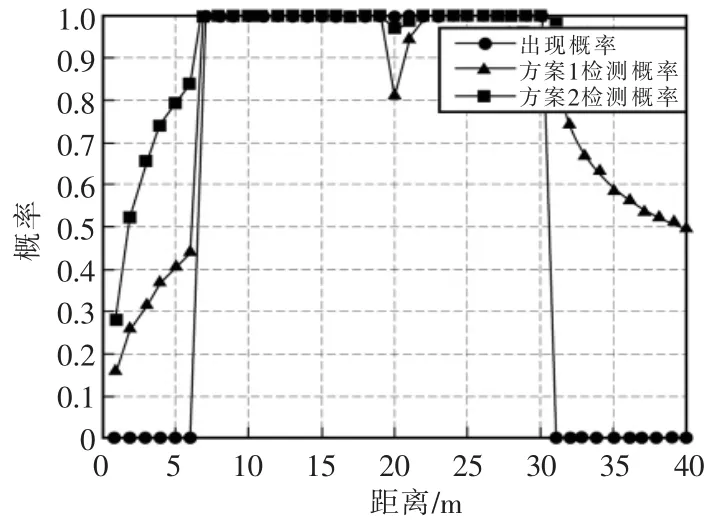
图3 目标检测概率的估计结果Fig.3 Estimation of target detection probability

图4 是目标跟踪与检测过程中目标的2 种模型交替出现的分布情况。可以看出在每一时刻目标的两种模型概率之和为1。图5 是整个跟踪过程中采样粒子的分布情况。可以看出当目标处于机动状态时，为了能够实时在线跟踪目标的航迹，需要采样更多的粒子去近似目标的真实轨迹。

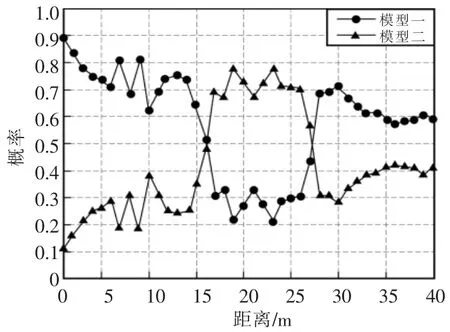
图4 两种模型概率变化过程Fig.4 Change of two models probability

图5 跟踪过程中粒子分布情况Fig.5 Particle distribution during tracking

4 结语

本文针对MMPF-TBD 方法在目标出现较强的机动时，目标的检测性能严重下降甚至出现漏检的问题提出了一种改进的多模型粒子滤波弱小目标检测前跟踪方法。该方法在目标出现机动情况时，通过设置一个加速度变量来实现对机动目标运动情况的匹配。此方法能够有效的避免两种模型之间的转换，提高了模型使用效率。仿真结果表明，当目标发生机动时该方法的检测性能明显优于MMPFTBD，能够提高机动目标的检测性能。