分块低秩图的遥感影像半监督分类应用*

祖宝开，夏克文+，牛文佳，姜晓庆

1.河北工业大学 电子信息工程学院，天津 300401

2.河北工业大学 河北省大数据计算重点实验室，天津 300401

3.济南大学 信息科学与工程学院，济南 250022

1 引言

近年来，随着科学技术的飞速发展，高光谱、高分辨率等遥感影像也逐步发展。它已经广泛应用于矿产资源勘探[1-2]、军事[3-4]、城市土地利用[5-6]、作物生长监测和生态环境检测[7-8]等方面。高分辨率图像具有较高的空间分辨率和丰富的空间信息。然而，数据量大、纹理特征复杂等问题很难解决。高分辨率图像数据的处理和信息提取一直是困扰研究者的难题[9]。

随着社会的发展，城市土地利用研究显得尤为重要[9]。城市土地利用变化对人类社会活动、城市经济发展和城市生态环境都是有影响的。机器学习方法是遥感图像分类中最有效的方法之一。主要分为无监督和监督分类方法[10]。监督分类利用先验知识来训练分类模型。与此相反，无监督分类不利用先验信息，通常也被称为聚类[10]。常用的无监督分类有k-均值和迭代自组织数据分析算法（iterative selforganizing data analysis techniques algorithm，ISODATA）[11]。监督分类方法有统计模型的分类方法、基于神经网络的分类方法[12]、支持向量机（support vector machine，SVM）[13]和相关向量机（relevancevectormachine，RVM）[14]分类方法。决策树方法包括基于信息熵增益的ID3算法[15]和利用信息熵增益比的C4.5算法[16]。

然而，大规模遥感数据难以获取大量标记数据。因为标记样本需要大量的人力和物力，且时间长，效率低。如果只利用少量的标记样本，训练出的学习系统很难有好的泛化能力[17]。而且，如果只使用标记样本来训练分类模型，则浪费了未标记样本所提供的有用信息。为了解决上述问题，半监督学习应运而生。半监督学习利用少量的标记样本和大量的未标记样本来学习分类模型。与监督方法相比，半监督学习可以有效地缓解“小样本”存在的问题[18-20]。Cai等人在线性判别分析的基础上提出了同时使用标记和未标记样本的方法，称为半监督判别分析（semisupervised discriminant analysis，SDA）[21]。但是基于图的半监督学习算法的性能在很大程度上依赖于图的构建过程。传统的图构造方法K近邻（K-nearest neighbor，KNN）和局部线性嵌入（locally linear embedding，LLE）等方法在很大程度上依赖参数的选择，同时利用欧几里德距离作为测度，容易受到噪声的影响。

Candès等人为了克服维数灾难，提出了稀疏表示与低秩理论[22-23]。稀疏表示和低秩理论的提出是为了解决信号重构的问题。低秩表示（low rank representation，LRR）法构造了一个无向图（这里称为低秩（low rank，LR）图），它根据低秩约束条件联合获取整个数据表示[24-25]，对噪声来说是鲁棒的。

低秩表示在遥感图像分类上的应用还很少，技术还不是很成熟，尤其是针对大规模遥感图像的分类。随着数据点（像素）的增加，LRR的计算复杂度呈指数增长。为了解决上述问题，将处理后的图像按像素划分为块（子集），并在每个块上进行低秩表示。然后，将特征表示子集组合成一个完整的特征图。应用K近邻来处理整个低秩图使之转换为对称矩阵，同时，K近邻最大程度地保留了图像的局部信息[26]。最后，应用半监督判别分析进行特征提取，可以充分利用标记样本的标签信息以及标记和未标记的数据点数据固有的几何结构信息。

对武汉市区WorldView-2遥感影像进行仿真分析。结果表明，基于块低秩图的特征提取方法是一种有效的方法。可以大大提高遥感图像分类的性能。在简单的最近邻分类器以及少量标签样本的情况下，也可以获得显著的分类性能。

2 基本理论和相关概念

2.1 低秩表示模型

LRR是将数据矩阵X=[x1,x2,…,xn]∈Rm×n表示成字典矩阵A=[a1,a2,…,am]（也称为基矩阵）下的线性组合，即：

其中，Z=[z1,z2,…,zn]∈Rl×n为低秩表示矩阵，zi为xi的低秩表示系数。为此，求解下列优化问题：

直接求解式（2）较困难。通过矩阵分解方法，式（2）转化为核范数问题：

其中，‖⋅‖*表示矩阵的核范数。

当用样本X本身作为字典，式（3）可转换为：

考虑到实际应用中数据的损坏或丢失和噪声等，目标函数转化为：

其中，噪声项选取l2,1范数。λ(λ＞0)平衡目标函数的两部分。

将式（5）转化为：

式（6）可以通过求解非精确增广拉格朗日乘子问题计算，即：

式中，Y1、Y2为拉格朗日乘子，μ＞0为惩罚参数。取得最优解（Z*,E*）后，利用Z*构造一个无向图的相似度矩阵，其中样本xi和xj为图的顶点，max([z*]ij,[z*]ji)为两个样本之间的权值。

2.2 半监督判别分析

线性判别分析算法（linear discriminant analysis,LDA）目标是找到一个投影子空间，使得在该子空间中，属于不同类别的点离得越远越好，而相同类别的点离得越近越好，即使类间离散度和类内离散度的比值达到最大[21]。

假设给定样本{x1,x2,…,xl}∈Rn，属于c个类别。LDA的目的是找到一个投影向量a，使aTSba和aTSta之间的比例最大化。

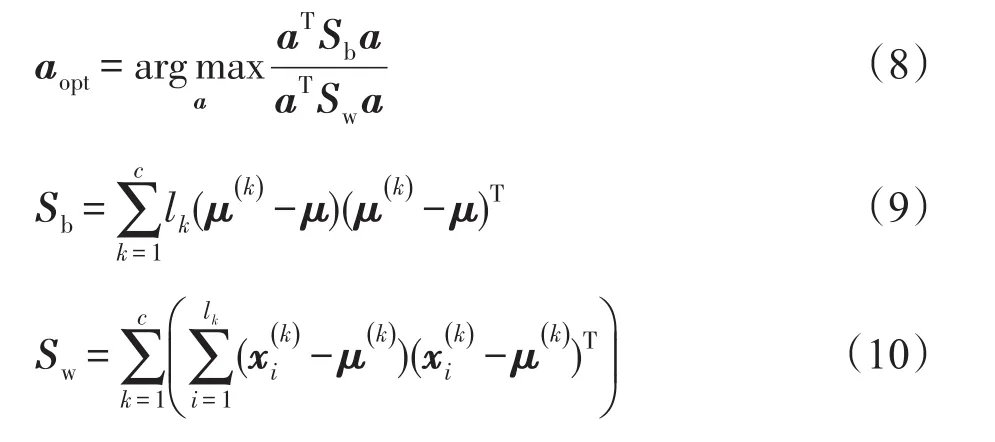
其中，μ是总样本的均值向量，是第k类样本的平均向量，lk是k类样本个数，是在第k类中的第i个样本，Sw和Sb分别为类内和类间散度矩阵。总散度矩阵,有St=Sw+Sb，那么式（8）中的目标函数为：

最优解a是与本征值问题的非零特征值对应的特征向量：

当训练样本不足时，过拟合将发生。防止过拟合的典型方法是加入正则化约束。Cai提出了半监督判别分析模型[21]。SDA的目的是找到一个投影来代表从标记的数据点中推断出判别信息，以及从标记和未标记的数据点中推断出的数据固有几何结构。具体而言，结合标记样本和无标记样本建立一个包含数据集邻域信息的图。利用拉普拉斯图的概念，该图提供了一个相对于数据流形局部几何结构的离散的近似值。因此，SDA优化算法可以保留流形结构[21]。SDA优化问题为：

其中，正则化项J(a)控制模型的学习复杂度，而系数α控制模型复杂度与正则化项间的平衡[21]。

J(a)是样本的邻接图矩阵，充分利用了先验知识。半监督学习算法的关键是一致性的先验假设[21]。传统的SDA用一个K近邻的图G模拟附近的数据点之间的关系。对于样本点xi和xj，在节点i和j之间设置一个边。相应的权重矩阵S定义为：

其中，Nk(xi)表示K近邻的集合。一般而言，映射函数在图上应该是尽可能光滑的。因此，那些稠密相连的子图可能拥有相同的标签。正则化矩阵可以定义如下：

其中，D是一个对角矩阵，它是S的列（或行，因为S是对称的）的总和。Dii=∑jSij，L=D-S是拉普拉斯矩阵。得到SDA的目标函数：

最优投影向量a由广义特征值问题求得：

其中Sb=XWl×lXT。

3 分块低秩图的遥感影像半监督分类

3.1 分块低秩图的半监督判别分析

在上面的章节中，研究了经典半监督判别分析和可以有效捕捉数据全局结构的低秩表示算法。基于上述启发，提出基于块低秩表示的正则化图。

对于特征向量X=[x1,x2,…,xM]∈RN×M,N是波段数（数据维数），M是像素数（样本数）。随着样本数量的增加，低秩表示计算时间呈指数增长。因此，通过分块理论来研究低秩表示问题。

让{g1,g2,…,gm}表示m个块图像的集合索引，其中每个gi存在S个像素。将同一块的向量放在一起，即X={Xg1,Xg2,…,Xgm},A={Ag1,Ag2,…,Agm}和E={Eg1,Eg2,…,Egm}。然后每个块的LRR优化问题转换为以下形式：

选择l2,1-norm作为误差项范数‖·‖l，它是

通过不精确增广拉格朗日乘子（augmented Lagrange multiplier，ALM）法[25]将增广拉格朗日函子最小化得到块低秩（block low rank，BLR）图然后将这些特征子集合并得到特征图矩阵Z={Zg1,Zg2,…,Zgm}=[z1,z2,…,zM]∈RS×M。

由于图邻接矩阵Z是不对称的，需要对称化处理才能满足SDA正则图的对称性要求。经典的对称化过程是矩阵转置和其本身的均值。然而，邻接图矩阵Z不是一个方阵。之前的研究表明，低秩K近邻（low rankK-nearest neighbor，LRKNN）图可以显著提高SDA[26]的性能。因此，K近邻算法的处理不仅解决了邻接矩阵对称化的要求，而且最大限度地保留了图像局部信息。因此，引入基于块低秩K近邻正则图对遥感影像进行半监督特征提取。

如果zi属于zj的k个最邻近点，或者zj是zi的k邻近点，那么zi和zj互为近邻点。这里使用热核方法为S分配权重，如下所示：

其中，Nk(zi)表示zi中的k近邻。

3.2 基于块低秩图的遥感影像半监督分类

给定一个属于c类的标记数据集和一个未标记数据集其中，第k类有lk个样本，假设{xi,…,xl}中的数据点根据自身的标签来排序。

基于块低秩图的半监督判别分析的步骤如下：

步骤1构造邻接图：构建X的低秩近邻图矩阵S，计算该图的拉普拉斯矩阵L=D-S。

步骤2构建标记图：为标记图构建权重矩阵Wl×l∈Rm×m，如下：

步骤3特征值问题：计算广义特征向量问题及其对应的非零特征值。

其中，X=[x1,x2,…,xl,xl+1,…,xm]，W的秩为d，得到d个特征向量a1,a2,…,ad。

步骤4SDA特征映射：让A=[a1,a2,…,ad]，A是一个n×c的变换矩阵。通过X→Z=ATX，数据可以映射到d维子空间。

由式（18）可以得到投影矩阵A：

其中，S是KNN变换之后的图。L=D-S是拉普拉斯矩阵。Sij是代表附近数据点关系模型的图形。Dii=∑jSij是对角矩阵D。

将W通过映射矩阵Φ映射到d维子空间中。

步骤5最后，执行K近邻分类器进行分类。

4 实验仿真与分析

实验的硬件平台是处理器为Intel Core CPU 2.60 GHz和8 GB RAM的机器，在Matlab 2016b上进行实验分析。

4.1 研究区概况

实验区为湖北武汉市辖区，地理位置在30°52′N～30°48′N与114°27′E～114°32′E之间（图1）。实验数据为WorldView-2影像数据，图像大小为2 500×2 500个像素的tif格式文件，影像质量良好，分辨率为2 m。WorldView-2影像是由美国Digital Globe公司发射的卫星获取的，该数据具有很高的分辨率。该卫星系统能够采集海量的影像数据，存储速度极快，而且定位精度极高，存储量极大。数据实验区内地物类型丰富，主要有河流、湖泊、建筑物、草地、农业用地、林地等。在武汉市中心城区附近，景观分布较为破碎，裸地和建筑用地、草地和林地等在空间上分布混乱。

Fig.1 Study area图1 研究区域

4.2 精度评价指标

分类精度评价非常重要，通过精度评价，能够直观、有效地获取分类结果中的信息。下面给出几种常用的遥感影像分类精度评价指标。

在遥感分类领域，经常使用混淆矩阵（confusion matrix）表示分类精度。对角线为正确分类的样本数，而非对角线表示错误分类的样本数。对角线的值越高表示结果越好。

分类精度（classification accuracy，CA）是指每个类别中正确分类的像素的百分比。总体准确率（overall accuracy，OA）指正确分类像素的百分比。平均准确率（average accuracy，AA）是计算所有类平均正确分类像素的百分比。为了使测量更加客观，使用Kappa系数来估计正确分类的像素的百分比。

制图精度（producer’s accuracy）是指分类器将整个影像的像元正确分为某类的像元数（混淆矩阵中对角线值）与该类真实参考总数（混淆矩阵中该类列的总和）的比率。

用户精度（user’s accuracy）是指正确分到某类的像元总数（对角线值）与分类器将整个影像的像元分为该类像元总数（混淆矩阵中该类行的总和）比率。

4.3 对比方法

为了验证本文方法的有效性，给出以下几个对比方法。为了公平，对比方法均包含KNN正则化处理过程。

块k近邻（blockKNN，BKNN）图：K近邻图（KNN图）每个顶点只与自己的k个近邻连接[26]。这里近邻数k设置为4。采用高斯核计算权重。

块局部线性嵌入（block locally linear embedding，BLLE）图：从局部线性嵌入方法通过最小化l2重构样本。将下式求得的局部线性重构系数作为样本连接权值[27]。

4.4 分类结果

由于分类结果对训练样本的选取有很大的依赖性，因此选取的训练样本要具有典型性和代表性。本实验借助ENVI处理软件选取各个地物特征明显的区域作为训练样本。从数值结果和视觉效果上进行了比较。一般来说，地物像元的一致性只能通过采样来检查，因为检查所有的像元是不现实的。验证样本可以通过野外实地调查或在高分辨率图像上通过目释解译的方法获取各个分类的地表真实感兴趣区[28-29]。由于实验影像分辨率为2 m，结合武汉市区的文字图片资料，在影像上选取6 270个验证样本和4 762个训练样本，如表1所示。表1给出每类分类精度、总体分类精度等评价指标。

Table 1 Classification results for different feature graphs表1 不同特征图的分类结果

表2～表5给出了混淆矩阵、制图精度和用户精度等。从表1～表5可以看出，BLR分类方法无论是在总体分类精度上还是Kappa系数上都比BSR、BKNN、BLLE方法有优势。Kappa系数比其他方法提高了约6个百分点。对比表1中的三种方法分类结果，可以看出基于BLR的影像分类结果比基于BSR的总体准确率提高了4.83%，Kappa系数提高了5.79%，说明基于BLR的分类能够较好提高高分辨率遥感影像的分类精度。虽然基于BSR方法的总体精度和Kappa系数较高，但从表3可以看出其对耕地、裸地和草地混分较为严重，耕地的制图精度只有70.35%。这是由于耕地和草地光谱较为相似，二者光谱特征在各个波段波动范围较大，在同一波段上反射率具有一定的重叠。稀疏表示图缺乏对数据的全局约束，每个样本求解过程相互独立。基于分块低秩图方法分类结果的总体精度比BKNN和BLLE方法的总体精度分别提高了5.57%和4.94%，Kappa系数分别提高了6.67%和5.92%。这是因为K近邻和LLE使用固定的全局参数，利用欧几里德距离来确定图的权重，其图矩阵结构对噪声敏感。

Table 2 Classification results of BLR graph method表2 BLR正则图方法分类结果

Table 3 Classification results of BSR graph method表3 BSR正则图方法分类结果

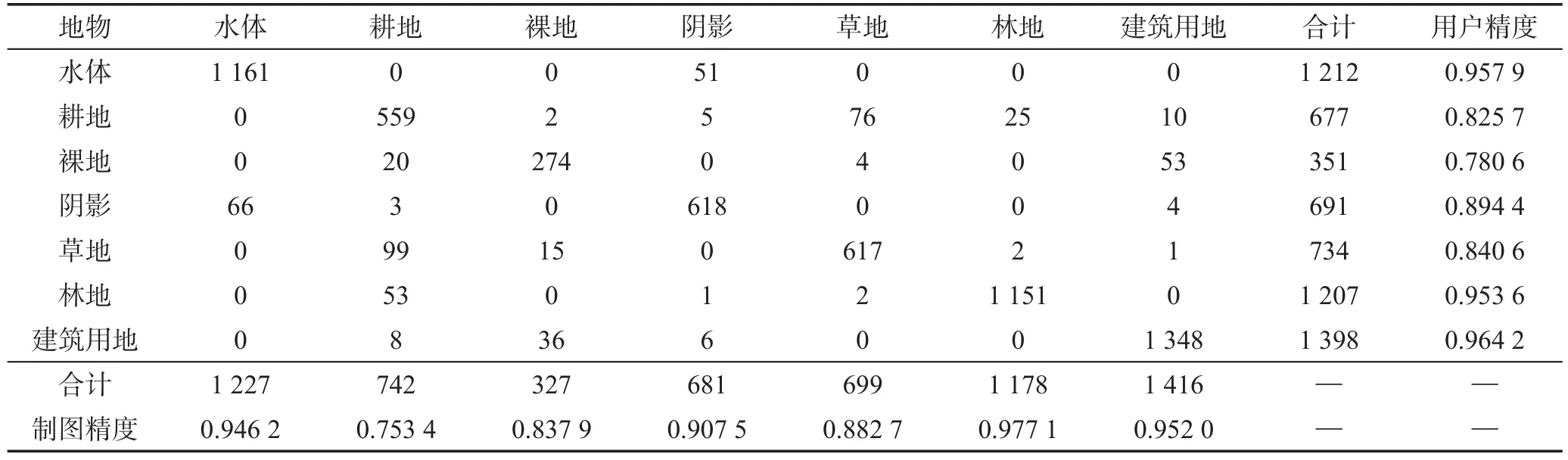
Table 4 Classification results of BKNN graph method表4 BKNN正则图方法分类结果

基于块低秩图的分类方法中耕地的制图精度达到90.43%，比稀疏表示方法提高了20.08%。这是因为LR图解决了对比方法的缺点，它根据低秩约束获得数据的全局信息，并且对噪声表现出鲁棒性。同时使用K近邻来处理整个低秩图，保留了数据的局部信息。因此，块低秩图方法显著提高了分类性能，对于大规模遥感影像是非常好的特征提取方法，能够在一定程度上改善耕地和草地的分类精度。然而，对于耕地、裸地和草地，由于在城市中样本数比较少，容易受到其他相对较大规模地物的混淆，导致基于块稀疏表示方法的分类精度没有较大的提高。由表2看出，基于BLR方法的各类制图精度都在90%以上，能够满足一般遥感影像制图精度的需求。因此，基于分块低秩的方法用于大规模遥感影像分类有一定的优势。

Table 5 Classification results of BLLE graph method表5 BLLE正则图方法分类结果

从视觉效果上对实验结果进行比较，如图2所示，基于分块低秩的分类方法和其他对比方法相比，有效地提高了影像的分类精度。例如，图中左上角水体区域以及右下角的裸地等误分为其他地物的问题得到了有效的改善，在一定程度上提高了影像分类精度，在影像分类上具有一定的可行性。遥感影像的分类受到众多因素制约，许多问题还有待进一步研究。实验中缺乏足够的实地调查信息和受目视判读的影响，样本地物类别判断上可能存在一定的偏差。实验只选择了光谱信息作为特征数据，在未来可以考虑将图像的纹理等信息引入到图像分类中。

5 结论

Fig.2 Land cover classification of Wuhan municipal district图2 武汉市辖区土地利用覆盖分类结果

本文把块低秩表示方法应用到高分遥感影像半监督分类上。为了降低计算复杂度，整个图像被分块并分别实现每个块上的低秩表示。因此，通过低秩表示保留了影像的全局结构。另外，K近邻算法保留了影像的局部几何结构。因此，基于块低秩正则图的半监督判别分析特征提取方法可以有效提高图像分类的性能。对武汉市WorldView-2影像进行实验表明，本文方法是有效和鲁棒的，可以实现大规模遥感影像的精确分类。