基于加速退化原理的光纤陀螺性能保持期评估方法研究

袁慧铮，李瑞珍，李星善，陆俊清，马 腾

(1.湖北航天技术研究院总体设计所，武汉 430040； 2.许昌高级中学，许昌 461000)

0 引言

光纤陀螺(Fiber Optic Gyroscope，FOG)具有全固态、体积小、质量小、启动快、可靠性高等优点，已经逐步取代三浮陀螺、挠性陀螺，在各型武器装备上得到了广泛的应用。大多数应用环境对光纤陀螺的要求为长期贮存、一次使用，需要保证其在长期贮存后依然保持良好的战技性能。作为具有精度要求的产品，其性能保持期既关系武器装备能否达到随时可用和能用的要求，又关系到不合理的标定、返修周期所造成的经济损失。

近年来，国内多家单位对光纤陀螺的关键参数、性能退化特性、冲击振动特性和热结构设计开展了研究工作[1-10]。国内在抗冲击振动结构设计和热结构设计方面，多采用理论分析加商用软件数值模拟的方式进行辅助设计。基于工程需求，国内的统计学者和工程技术人员对于参数长期变化问题，即退化问题进行了研究并应用于光纤陀螺中，但是对加速退化试验寿命长度验证的方案设计和加速寿命试验数据的分析处理方法较少涉及。

国外对加速退化试验的研究始于20世纪80年代，近30年来，Nelson、Meeker、Escobar等对加速退化试验技术的理论和方法进行了深入的研究。20世纪90年代初，加速退化试验逐渐引起国内统计学界和可靠性工程学界的广泛关注[11]。加速退化试验是在失效机理不变的基础上，通过提高应力水平来加速产品性能退化，利用高应力水平下的性能退化数据来估计产品在正常使用应力下的可靠性特征。

因此，本文选择光纤陀螺整机为研究对象，通过加速退化的手段得到其零偏和标度因数等数据，并利用小子样统计分析的方法得到其性能保持期。

1 光纤陀螺退化特性分析

在光纤陀螺的长期贮存过程中，随着时间的推移，光纤陀螺中光学器件、电子器件性能的退化最终都会影响到光纤陀螺的性能，具体表现在光纤陀螺相关性能指标的下降，直至不能满足要求；相关指标超差，可以认为发生了失效。在实际应用中，对导航和控制影响最大的是陀螺的零偏和标度因数，因此，本文的关注点集中于陀螺的零偏和标度因数。

1.1 零偏退化特性分析

通常情况下，光纤陀螺零偏相关的误差可以分为零偏常值性误差、零偏随机性误差、零偏环境敏感性误差和量化噪声等。本文重点关注的是光纤陀螺的常值误差，即陀螺在输入为0时的输出均值。通过在近似相同的条件和测试方法下，多次重复测量得到零偏之间的标准差或极差，具体的数值因测试条件和重复周期的不同而有所差异。在理想条件下，闭环干涉式光纤陀螺的常值误差应该为0，但由于白噪声、散粒噪声、光源相对强度噪声、电噪声、热相位噪声、量化噪声、偏振误差、非线性克尔效应误差、背向反射引起的误差、电路解调漂移等各种因素的影响，其实际测量值并不为0。随着贮存时间的增长、光源及光传输通道性能的劣化、电子元器件性能的退化，均会造成零偏呈现一定程度的退化。

1.2 标度因数退化特性分析

相比较而言，光纤陀螺的标度因数与光电器件参数的关系较为简单，具体为

(1)

式中，λ为光信号波长，L为光纤敏感环长度，D为光纤环有效直径，Vpp为阶梯波的峰峰值电压，Kfp为Y波导的电压调制系数。其中，VppKfp=2π，光纤陀螺中通过第二闭环控制来保证2π电压的准确性。因此，光纤陀螺标度因数的变化主要取决于光信号平均波长、光纤敏感环长度和光纤环有效直径的变化。

2 光纤陀螺退化的可加速性分析

光纤陀螺是光电一体的精密仪器，其整机失效机理比较复杂，目前从机理上对其整机可加速性进行分析论证比较困难。通过调研相关文献[12-13]，有相关学者采用可靠性摸底试验的方法对光纤陀螺性能退化可加速性进行一定的探索研究。由于光纤陀螺的敏感应力是温度，且具有可加速性。因此，采用温度作为主要加速应力对光纤陀螺性能退化的可加速性进行摸底，得到如下结论：

1)在同一温度应力的长期作用时间内，光纤陀螺的零偏值也存在着缓慢的退化趋势。这种变化是由陀螺内部自身原因造成，反映了一种长期环境应力作用下的累积性损伤，是不可逆现象。因此，陀螺零偏值的变化体现了陀螺性能的退化。

2)同一温度下各试验样本之间变化率有所不同，这是由于生产工艺等原因造成的个体一致性差别。但是对于同一试验样本而言，随着温度应力的提高，其零偏变化率也相应变大，且3只样本规律基本一致，显示出光纤陀螺性能下降速率与温度应力具有单调相关的变化趋势。

通过以上分析，得出以下推论：

1)随着贮存时间的增长，应力逐渐累积，光纤陀螺的零偏和标度因数存在退化趋势。

2)光纤陀螺性能参数退化的主要原因是光学器件和电子器件老化。

3)在高温条件下光纤陀螺的退化具有可加速性。

4)光纤陀螺通过改进工艺，可以延长其性能保持期，但其服从的退化统计规律是相同的。

3 试验方法及流程

3.1 试验应力确定

光纤陀螺的贮存主要是库房贮存，选择标准库房贮存条件作为加速效应评估基准，平均环境温度为25℃，温度波动范围为15℃～30℃。由于采用高温作为加速退化试验的加速应力，因此，选择25℃作为加速效应评估的基准。

光纤陀螺仪采用加速退化试验方法，需要利用试验测试数据解算性能参数退化模型和加速模型参数。获取加速退化函数后才能预测实际贮存条件下的性能参数超差时间，确定对象贮存性能保持期。由于选择高温作为加速退化试验的应力，而单温度恒定应力模型中包含2个参数，为了采用最小二乘法或极大似然估计方法求解模型参数，至少需要3个应力水平的测试数据，至少选取3个温度应力水平。因此，选取3个温度应力水平进行试验。

3.2 最大试验应力的确定

试验应力量值的选取不宜过低或过高，试验应力量值过低将导致试验样品的性能退化趋势不明显；反之，则会使试验样品失效机理发生变化，甚至损坏试验样品，这两种情况都达不到加速退化试验的目的。

确定最大应力量值时，应充分进行调研以获得产品的完整的组成和耐受环境条件的信息，尽可能避免调研不足和考虑不充分造成的疏漏；同时，在确定最高应力时应留有更多的余量，避免疏漏可能造成的不良影响。根据某型光纤陀螺组成部分在非工作状态下极限应力范围的调查可知，光纤陀螺仪中的全部组件(包括敏感组件)能够耐受的温度范围是-40℃～+85℃，为保有余量，防止光纤陀螺仪在温度临界值发生破坏，选取最高温度应力为+80℃。

3.3 应力量值的选取

在确定了最大应力量值后，其他各组温度应力的确定，主要考虑3个因素：

1)确定最低应力水平组的温度应力，最低应力不应过低，否则将导致该组加速效应过小，所需试验时间可能会加长；

2)根据应力水平组数，依据等分布原则，选取温度应力量值；

3)检查各组温度梯度，相邻组间的温度梯度应不低于10℃，当温度梯队过小时，可适当调整最低温度和最高温度，重新计算其他各组温度应力。

通过上述步骤，应能确保最高温度安全和最低温度加速效应可取，且温度梯度大小合适。

根据加速试验温度梯度的设计经验，为提高加速模型参数解算的准确性，采用式(2)计算得到应力量值

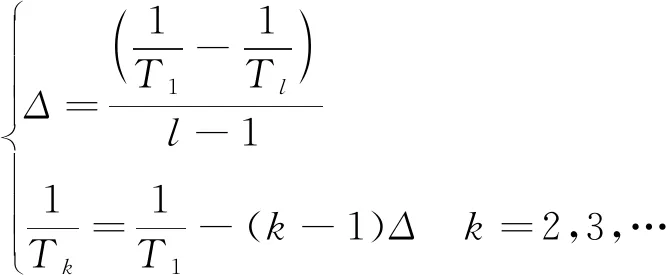
(2)

经计算，选取最高温度应力为80℃，最低温度应力为60℃，则对应的其他各组温度应力如表 1所示。

表1 温度应力量值的选取

根据计算结果可知，应在60℃、69.7℃、80℃这3个应力水平下开展加速试验，但为了试验便于操作，选取60℃、70℃、80℃作为加速应力条件。

3.4 试验样品分配

从模型参数解算的需要和评估准确程度的角度考虑，采取温度应力进行加速试验，所以，每型样品需要分成3组开展加速试验。为保证试验结果的预测精度，每组应保证2个试验样品，相互之间可以比对分析，则共需要6个试验样品。试验样品的分配如表 2所示。

表2 加速退化试验样品分配情况

3.5 试验流程

试验前应对待试陀螺进行充分的老炼和测试，确认陀螺已达到性能稳定期，具备参试条件。试验中应对发现的故障及时进行处理和甄别，确认产品是否具备继续试验条件，详细流程见图 1。

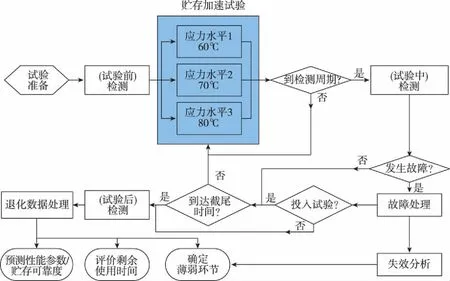
图1 光纤陀螺加速退化试验流程Fig.1 Accelerated degradation test process of FOG

4 试验数据及分析

4.1 试验数据获得

基于ASE光源设计选定用于试验的光纤陀螺，产品编号分别为X001、X002、X003、X005、X006、X007，设计指标为零偏稳定性优于0.01(°)/h，标度因数稳定性优于3×10-5，产品的试验分组信息和试验前测试数据如表3所示，表明参试产品是满足设计指标要求的。

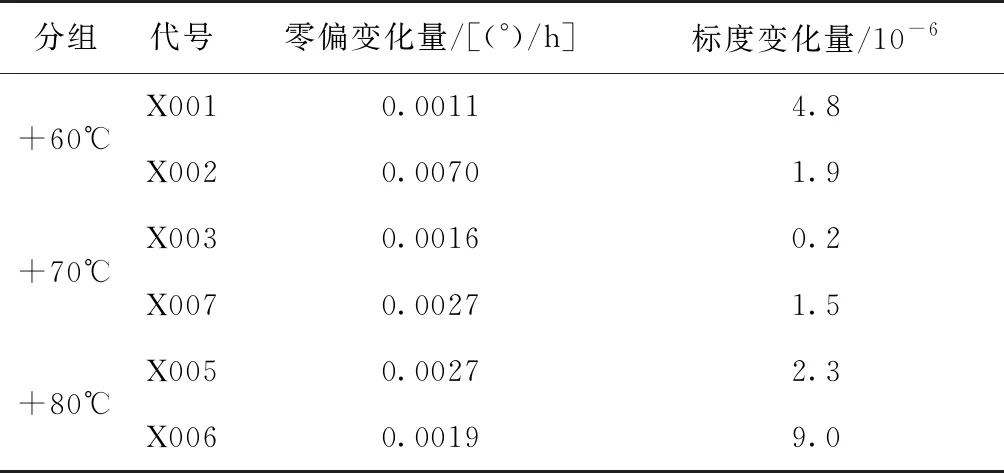
表3 光纤陀螺测试前参数测试及分组信息

样品于2016年5月1日起在温箱中进行各温度不通电状态的贮存，并进行周期性的零偏和标度因数测试，持续时间约3个月，于2016年9月12日结束。其中X006陀螺在首次测试时，产品无输出，经判断和检查，该问题是由于电子元器件偶发性故障引起的，无法进行后续测试。因此，本试验仅采信其余5只产品的试验数据，不影响加速退化试验结果的正常评估。

4.2 试验数据整理

对样品的试验数据整理步骤如下。

1)选定0时刻，将试验记录表中的日期转换成时间(单位d)。各组试验中样品选定的0时刻基准如表4所示。

表4 样品测试的0时刻基准

2)将试验原始记录中的零偏(B)和标度因数(K)转换为零偏变化量(ΔB)和标度因数相对变化量(ΔK)。其中

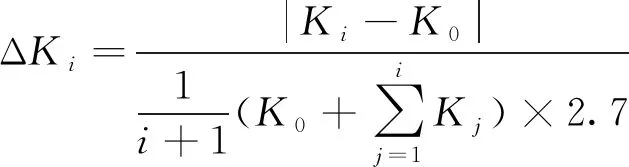
(3)

式(3)取了统计方法中的一个近似，认为统计数据的极差近似于3σ值，而3σ值与1σ值之间存在2.7倍的近似关系。

零偏(B)的变化量(ΔB)不能超过(0.01(°)/h，1σ)，即零偏变化量的超差判据为

(4)

标度因数(K)的相对变化量(ΔK)不能超过(3×10-5(^/(″))，1σ)，即标度因数相对变化量的超差判据为

(5)

4.3 试验数据处理

4.3.1 变化趋势分析

根据整理后的试验数据绘制散点图，分析零偏变化量(ΔB)和标度因数相对变化量(ΔK)的变化趋势，结果如图2所示。可以看出，样品的标度因数相对变化量(ΔK)存在较为一致的退化趋势，其中60℃和70℃下的样品向下退化，80℃的样品向上退化，在做数据处理时统一对其取绝对值。

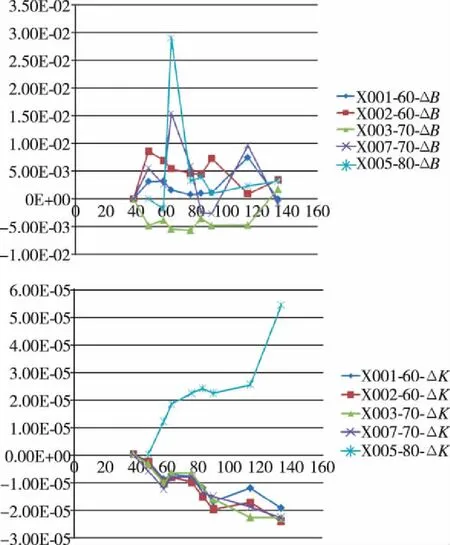
图2 样品的ΔB和ΔK分布图Fig.2 ΔB and ΔK distribution of the sample

4.3.2 数学模型求解

根据相关的研究结论[14]，在开展加速试验进行数据处理时，对于零偏变化量(ΔB)选用灰色系统模型进行性能保持期的预测。这是由于灰色系统理论的优势在于将随机量看作是在一定范围内变化的灰色量，按适当的方法将原始数据进行处理，将灰色数变换为生成数，进而从生成数得到规律性较强的生成函数，从而突破了概率统计的局限性，常用的灰色系统模型包括GM(1,1)模型。对于标度因数(ΔK)相对变化量，其规律性较强，可以采用线性退化模型进行性能保持期的预测。

性能保持期与应力的关系采用Arrhenius方程进行描述

(6)

对样品的零偏变化量(ΔB)和标度因数相对变化量(ΔK)分别求解退化模型和加速模型。

4.3.2.1 样品零偏变化量(ΔB)

(1)退化模型求解

灰色系统模型[14]用于处理间隔时间相等的数值序列预测问题，但由于开展加速退化试验实际的测试时间是不等的，因此在采用灰色系统模型建模时应对其进行近似处理。经计算，60℃下产品的平均寿命为339d，70℃下产品的平均寿命为339d，80℃下产品的平均寿命为135d，则根据Arrhenius模型,可以根据3组数据拟合求得A和Ea的值，A=0.0005，Ea=0.456eV。加速模型求解结果如图3所示。

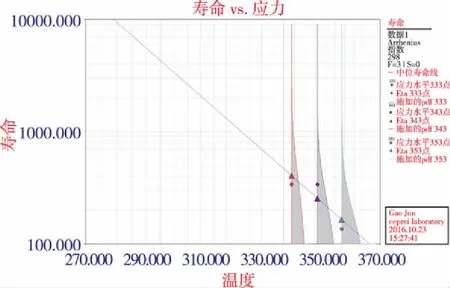
图3 样品ΔB加速方程拟合结果Fig.3 Fitting result of ΔB based on acceleration equation

根据激活能可以计算各个加速应力条件下相对于常规贮存条件的加速因子，将外推失效时间折算到标准贮存环境下，失效时间折算如表5所示。

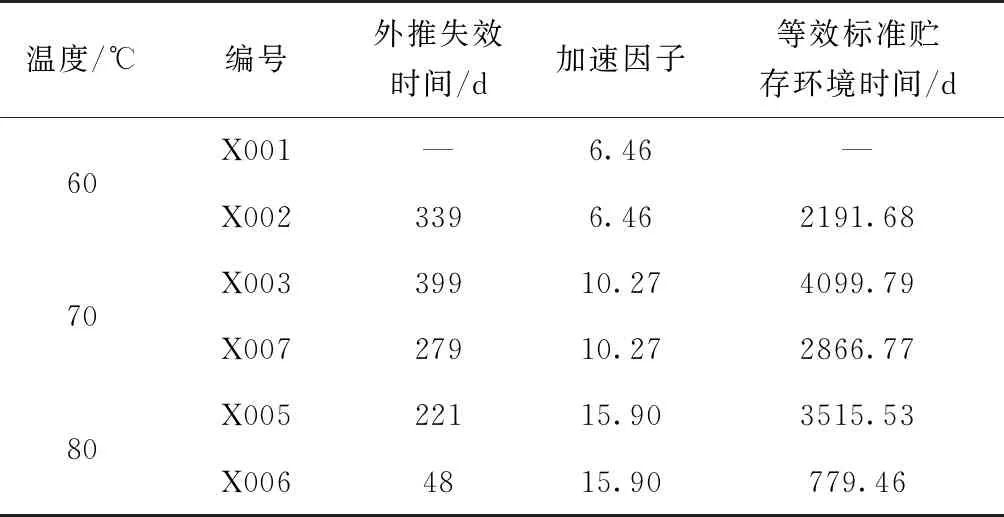
表5 样品ΔB失效时间折算

根据Weibull分布的表达式，可以求出分布参数m=2.58,η=3025.34,并计算得到样品零偏的平均性能保持期为

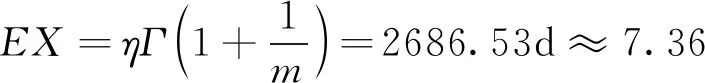
(7)

样品ΔB分布模型的对数概率密度曲线如图4所示。

4.3.2.2 样品标度因数相对变化量(ΔK)

(1)退化模型求解

样品标度因数相对变化量(ΔK)的变化趋势用线性退化模型求解，样品X006在80℃下试验至第48d时失效。经外推，60℃下产品的平均寿命为171.49d，70℃下产品的平均寿命为160.64d，80℃下产品的平均寿命为73.08d。则根据Arrhenius模型,可以根据:3组数据拟合求得A和Ea的值，A=0.000075，Ea=0.424eV。加速模型求解结果如图5所示。

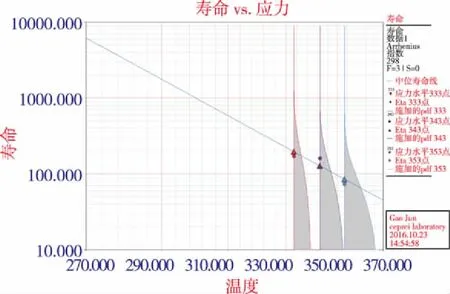
图5 样品ΔK加速方程拟合结果Fig.5 Fitting result of ΔK based on acceleration equation

根据激活能可以计算各个加速应力条件下相对于常规贮存条件的加速因子，将外推失效时间折算到标准贮存环境下，失效时间折算如表6所示。根据Weibull分布的表达式[15]，可以求出分布参数m=4.82,η=1220.60，平均失效时间为

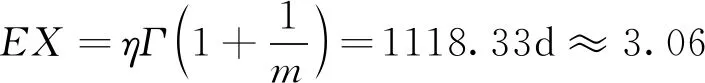
年 (8)

样品ΔK分布模型的对数概率密度曲线如图6所示。

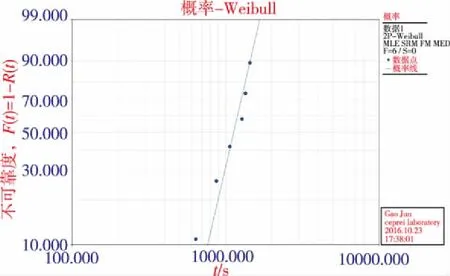
图6 样品ΔK分布模型的对数概率密度曲线Fig.6 Log-probability density curve of ΔK

5 结论

对光纤陀螺开展加速退化试验，根据对小样本条件下加速退化试验数据的处理，得出以下试验结论，基于ASE光源的光纤陀螺，可以在0.01(°)/h的精度指标上，实现长达3年的性能保持期。

从更严谨的角度来说，进行加速退化试验，还需要进行以下工作：

1)对数据进行一致性检验，确定试验的截尾时间等工作；

2)本文中只有6只产品进行试验，样本量偏少，偶发性因素容易影响整体评价效果；

3)随着光纤陀螺工程化应用越来越广泛，对陀螺性能保持期的评估更应该采用大样本、自然贮存与加速退化相对照的方式进行交叉验证，以便得到更为准确的描述模型。