一种卫星导航模拟器置信度评估方案及应用

王 勋，洪诗聘，左启耀，杨晓昆

(1.北京自动化控制设备研究所，北京 100074； 2.中国航天科工信息技术研究院，北京 100070)

0 引言

卫星导航模拟器用来模拟不同条件下卫星导航系统播发的导航卫星信号，能够模拟复杂的载体运动场景，可以为卫星导航接收机的研制开发、测试提供仿真环境[1]。卫星导航模拟器产生导航信号的正确性和可信度，是评估卫星导航模拟器优劣的关键。

卫星导航模拟器是导航卫星应用的综合仿真系统，涉及物理建模、数仿、时频以及射频等诸多方面。目前，针对卫星导航模拟器的置信度评估方法鲜有研究。通常，对仿真系统置信度的评估方法[2]主要包括三类：模糊综合评价法、层次分析法以及模糊层次分析法。其中，模糊层次分析法所得到的置信度评估结果相对于其他两类更具客观性和科学性。因此，可采用模糊层次分析法对卫星导航模拟器系统进行置信度评估。然而，卫星导航模拟器系统复杂，按照模糊层次分析法，执行系统置信度评估前，需要对整个模拟器系统进行分解，分解为若干子系统和模型，分层次、分阶段进行置信度评估，然后再考察整个系统的置信度。因此，整个系统置信度评估的基础是对子系统或模型的置信度进行评估。现有仿真模型评估方法中，最常用[3-8]的是置信区间法、谱估计法以及相似度法。相似度法是依据实际系统与仿真系统的诸多相似元来计算整个仿真系统的置信度，该方法对动态和静态模型均适用。卫星导航模拟器仿真模型多样，动态模型和静态模型均涉及。因此，相对于置信区间法和谱估计法，宜选用相似度法计算其各个模型的置信度。

基于此，本文提出了一种基于对数最小二乘的模糊层次分析法和相似度法相结合的置信度评估方案。即首先利用模糊层次分析法将卫星导航模拟器仿真系统分解为诸多子系统或模型后，采用相似度法计算各个子系统或模型的置信度，而后再结合模糊层次分析法逐级计算出整个模拟器系统的总置信度。

1 卫星导航模拟器原理与构成

卫星导航模拟器由控制主机与模拟器主机组成。控制主机运行显控软件，显控软件主要包括数仿、控制与显示3个部分。其主要功能是仿真任务设计与各类仿真数据生成；建立和维护卫星导航系统所需要的数学模型；自主生成或接收外部用户轨迹数据；进行仿真数据和仿真过程状态的图表、曲线等可视化显示。卫星导航模拟器结构如图1所示。

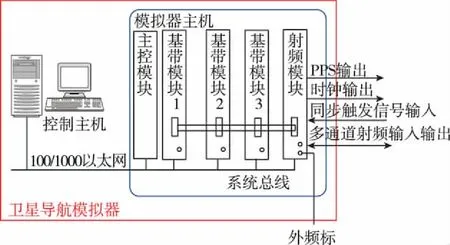
图1 卫星导航模拟器系统结构图Fig.1 Structure chart of GNSS signal simulator system

模拟器主机接收显控软件仿真生成的观测数据和导航电文，负责生成射频导航信号。整个模拟器系统中的核心功能是仿真功能，其基本功能是实时生成各类仿真数据，主要包括仿真任务设计；建立和维护卫星导航系统所需要的空间坐标系统及其转换的数学模型；通过自己生成或外部用户轨迹数据导入，进行仿真数据和仿真过程状态的曲线、图表等可视化显示。

图2是卫星导航模拟器的工作架构。根据功能特性与可评估性，卫星导航模拟器可划分为数仿、时频和射频模块3个主要部分。时频模块可选择使用内外时钟作参考，经过频率分配器和综合器后，供数字处理和射频模块使用。数仿模块实时计算用户轨迹参数，然后根据空间传播参数配置(电离层、对流层、卫星星座等)完成卫星星座和轨道仿真、空间环境仿真，生成导航电文和观测数据，发送给射频模块，经上变频、功率增衰、合成与功分后输出。同时，存储卫星星座监控、载体运行监控以及卫星导航信息监控等数据文件至共享数据区。

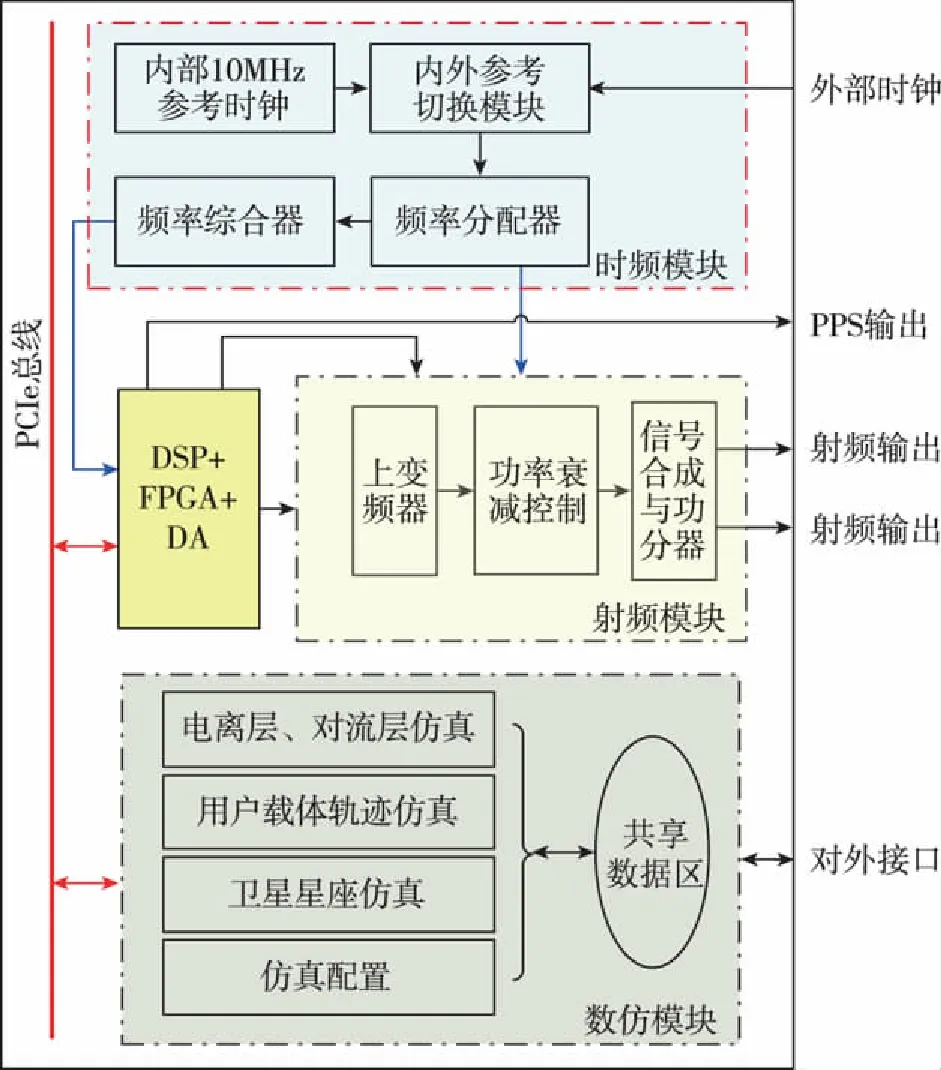
图2 卫星导航模拟器工作架构Fig.2 Architecture scheme of GNSS signal simulator system

2 卫星导航模拟器置信度评估方案设计

2.1 基于对数最小二乘的模糊层次分析法

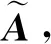
i,j=1,2,…,n;i≠j,k=1,2,…,dij

(1)

(2)

经去模糊化[9]后的归一化权重向量为

(3)

得到归一化后的权重后，需要进一步进行综合评估。构建模糊评判模型，其有3个基本要素：论域集U={u1,u2,…,un}，评价集V={v1,v2,…,vm}和模糊变换。其中，模糊变换即模糊映射

f:U→F(V)ui|→f(ui)=(ri1,ri2,…,rim)∈F(V)

(4)

由映射f可诱导出一个模糊评判矩阵

(5)

若确定了归一化权重向量W，可再由R诱导一个模糊变换

TR:F(U)→F(V)W|→TR(W)=W°R

(6)

进一步，为兼顾各元素的权重，使评价结果充分体现被评价对象的整体特征，引入M(⊕,•)模糊算子，构成综合评价集B

(7)

式中，Wi构成归一化权重向量W，即有W={W1,W2,…,Wn}。

2.2 相似度方法

设系统M由k个要素组成，系统N由l个要素组成，系统M与N之间有n对相似元，每对相似元的相似程度记为q(μi),i=1,2,…,n，每一相似元对的影响权重为βi，则定义系统相似度为

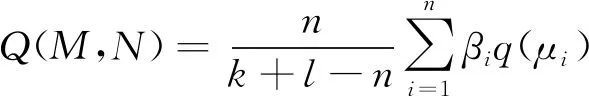
(8)

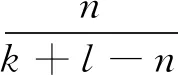
仿真系统置信度是在总体结构和行为水平上能够复现实际系统的可信性程度。相似度越大，仿真系统和实际系统的贴近度越高，反之亦然。因此，在某种意义说，相似度可用来代替相似元对应特性上的仿真系统置信度。

2.3 基于模糊层次分析和相似度的置信度评估方案

根据基于对数最小二乘的模糊层次分析法[9]和相似度方法[10]的特点，设计如下卫星导航模拟器的置信度评估方案。图3是基于对数最小二乘的模糊层次分析法和相似度法结合的置信度评估方案框图。

图3中，评估方案由模糊层次分析方法和相似度方法结合构成。前者将卫星导航模拟器仿真系统分解为若干个评估子目标，每个子目标对应各自的子系统或仿真模型。同时构建递阶层次体系和模糊判断矩阵，经解算、归一化后得到各个仿真模型的权重向量W。而对于模拟器仿真系统的每个仿真模型，依据其属性确定出若干相似元，构成相似元集。同时，使用模糊层次分析方法对每个仿真模型的若干相似元的权重进行计算，通过加权平均后得到仿真模型的置信度。按照此方法，依次计算每个相似元集的权重向量W1,W2,…，Wn。至此，可以得到各个仿真模型的相似度和权重，加权平均后得到整个模拟器系统的总置信度。

根据上述分析，该评估方案的执行步骤可归结如下：

Step1：构造递阶层次结构体系

根据系统所包含的因素及相关关系，分解出关键性评判准则，并构成多层次指标体系结构。设系统评估子目标的论域集为U

U={u1,u2,…,um}

(9)

式中，ui为第一层(最高层)中的第i个子目标，它由第二层中的p个子系统或模型决定，即有

图3 基于对数最小二乘的模糊层次分析和相似度的置信度评估方案Fig.3 Confidence evaluation scheme based on LLS FAHP and similarity method

ui={ui1,ui2,…,uip},i=1,2,…,m。

Step2：确定权重分配集

利用对数最小二乘层次分析法计算权重，经去模糊化处理后，得到非模糊的归一化权重向量。

通过上述步骤，可分别得到子系统或模型的权重分配集为

W={W1,W2,…,Wm}，Wi={wi1,wi2,…,wip}

(10)

式中，Wi和wij满足

(11)

Step3：模型相似度计算

根据模型特性，确定使用静态模型或动态模型计算各个模型的相似度，从而得到各个模型的相似度矩阵Ri为

Ri=[ri1ri2…rip]T,i=1,2,…,m

(12)

由于系统通常存在复杂的不确定因素[11]，必要时需要在一级模糊综合评判的基础上，进一步引入二级模糊综合评判，以得到二级综合评判结果。

Step4：选择加权平均算子进行综合评判

构造一级模糊评估集为

Bi=Wi°Ri=[wi1,wi2,…，wip]°[ri1ri2…rip]T

=bi,i=1,2,…,m

(13)

其中，°为加权平均型算子；Wi为子目标权重集；Ri为子系统或模型层次的相似度。>

为了进一步得到高层次的综合评价，必须进行二级模糊综合计算，建立如下二级模糊综合评估模型

(14)

这样，在一级模糊评判的基础上，逐级得到整个模拟器系统的置信度评估结果。

3 卫星导航模拟器仿真模型及置信度评估结果

3.1 卫星导航模拟器置信度评估体系构建

卫星导航模拟器由时频模块、数仿模块以及射频模块组成。卫星导航模拟器各个模块对时钟的要求不一，首先要求的是时钟同源，特别是基带信号生成模块，为了能生成高精度的卫星信号，时钟的准确度和稳定性直接决定了系统的时序逻辑、中断控制和同步脉冲的正确执行。

数仿模块的基本功能是实时生成各类仿真数据，其涉及的仿真模型包括卫星星历误差模型、电离层延时模型、对流层延迟模型以及用户轨迹模型。

射频模块负责产生系统内需要的各种时钟信号和本振信号。上变频通道能够完成上变频，滤波放大，信号合成模块将各个频点信号合成后输出射频信号。未调制的频谱纯度、相噪以及谐波抑制直接决定了模拟卫星射频的信号质量。

根据以上组成，建立卫星导航模拟器系统置信度体系，在结构上可分为三层：目标层(A)、中间层(B)和底层(C)，如图4所示。其中，目标层即为卫星导航模拟器系统最顶层；中间层模型包括时频模块(B1)、数仿模块(B2)以及射频模块(B3)；底层模型包括时钟稳定性(C1)、时钟准确度(C2)、卫星星历误差模型(C3)、电离层延迟误差模型(C4)、对流层延迟误差模型(C5)、用户轨迹模型(C6)、未调制的频谱纯度(C7)、未调制的频率相噪(C8)和谐波抑制(C9)。

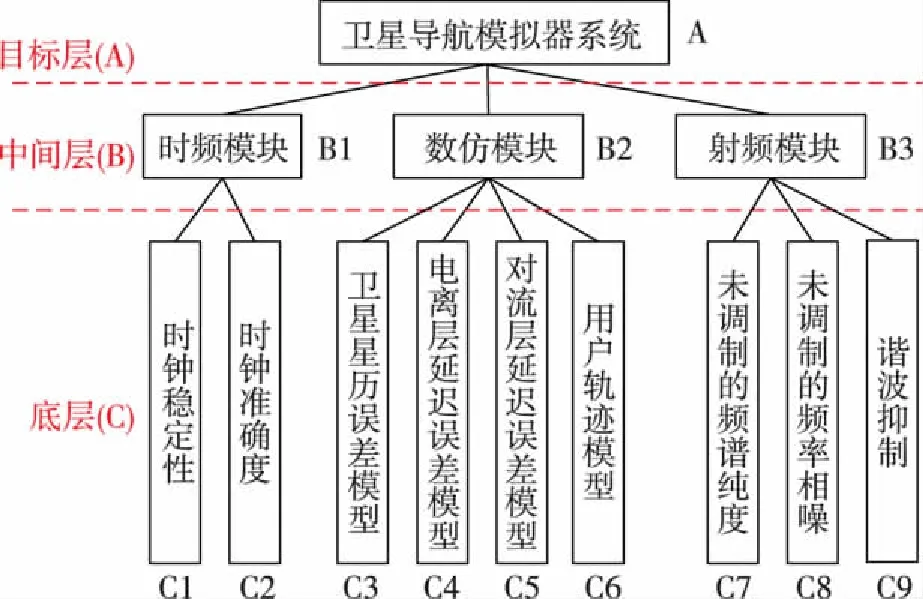
图4 卫星导航模拟器置信度层次结构图Fig.4 Hierarchical structure of GNSS signal simulator for the confidence evaluation

根据卫星导航模拟器置信度的层次结构可知，该系统的总体置信度由3个中间层模型的置信度综合决定，而各个中间层模型的置信度由构成该模型的各底层模型置信度决定。因此，在对卫星导航模拟器进行置信度评估时，首先要对各底层模型进行相似度计算，以此作为模型置信度，然后再得到上一层模型置信度，并综合获得卫星导航模拟器系统的总体置信度。

3.2 子系统或模型权重计算

邀请3位专家利用三角模糊数对各指标之间的相对重要性做出判断，且对于任意2个指标之间的重要性进行对比，至少有1位专家给出判断，得到准则层和指标层的模糊判断矩阵，分别如表1～表4所示。

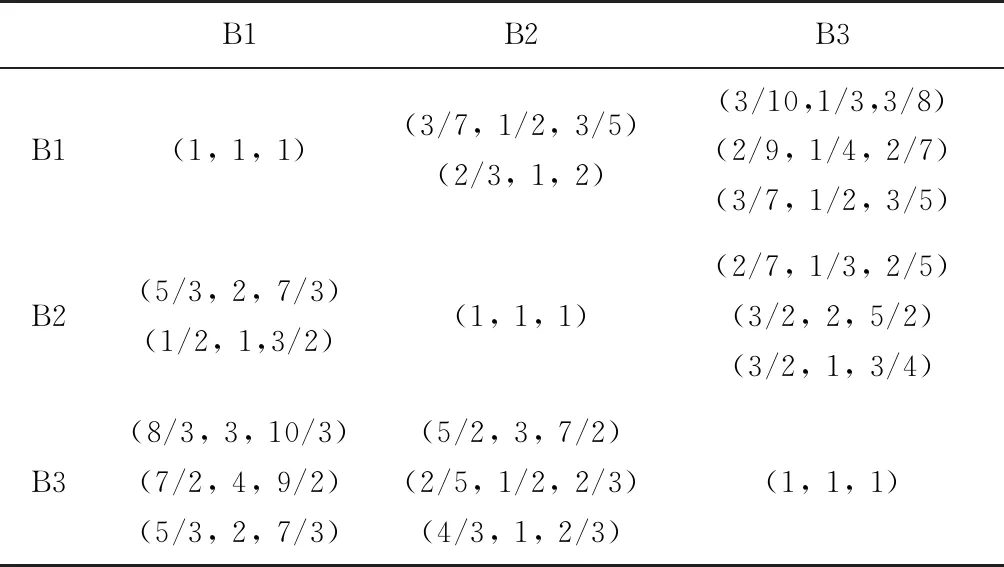
表1 主指标(A)的模糊判断矩阵

表2 时频模块(B1)的模糊判断矩阵

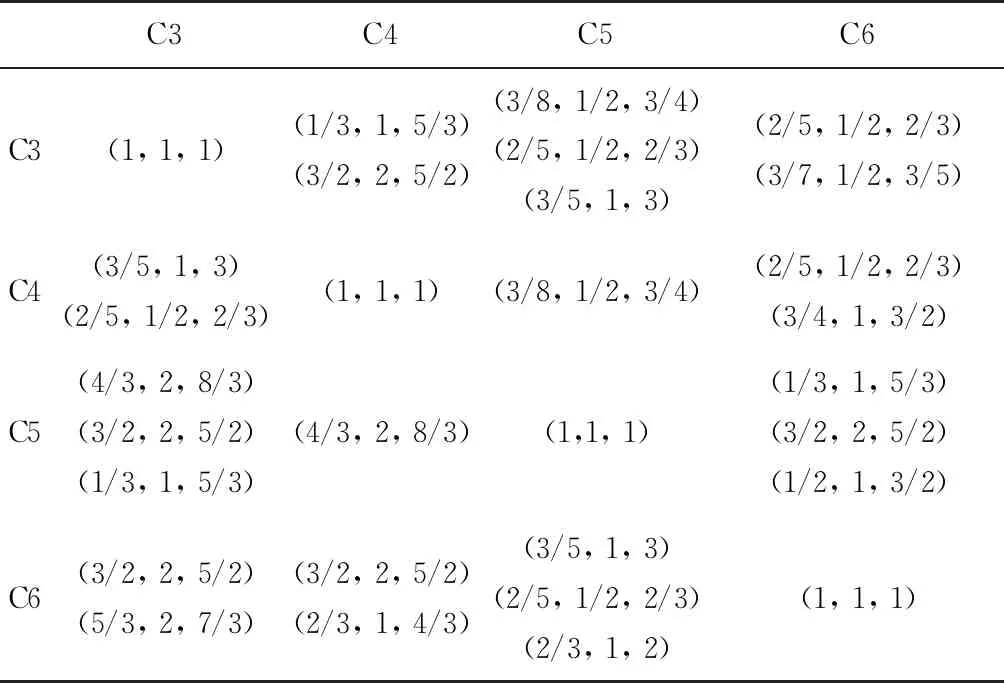
表3 数仿模块(B2)的模糊判断矩阵

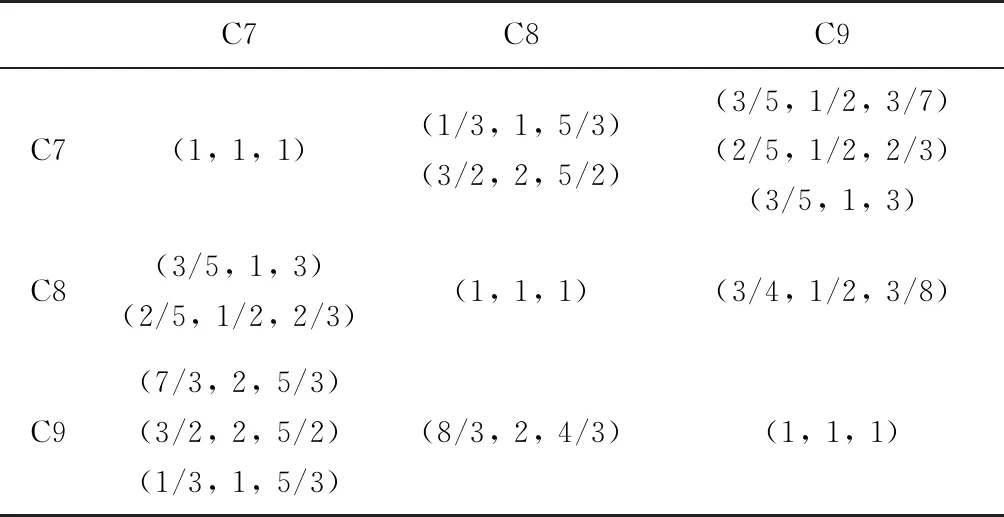
表4 射频模块(B3)的模糊判断矩阵

利用基于对数最小二乘层次分析法计算各模糊判断矩阵的权重向量，权重向量的计算结果如表5～表8所示。

表5 主指标(A)的子指标权重(w1～w3)

表6 时频模块(B1)的子指标权重(w11～w12)

表7 数仿模块(B2)的子指标权重(w21～w24)

表8 射频模块(B3)的子指标权重(w31～w33)

由表 5可以看出，数仿模块的权重相对较高，这是由于时频模块和射频模块很大程度上依赖于设计保证。在评估模拟器置信度时，可以将某些指标特性权重淡化，如时钟准确性和稳定性，与真实卫星比较差异较大，但模拟器运行时间通常相对较短且其仿真精度、置信度不直接依赖于时钟源特性，因而其权重偏小。不同于时频模块和射频模块，数仿模块的权重较大，这是由于数仿模块涉及诸多模块，其模型的准确性直接决定模拟器系统的置信度。可见，基于对数最小二乘层次分析法得到的权重可以代表各子指标之间的相对重要性，权重分配较为合理。

3.3 子系统相似度计算

3.3.1 电离层延迟误差模型相似度计算

1)电离层延迟误差模型

利用电离层误差模型是卫星导航模拟器产生电离层延迟误差的常用方法。最常用的电离层误差模型是Klobuchar电离层模型，该模型分下述两种情况：

① 天顶方向(E=90°)的电离层延迟误差如下所示

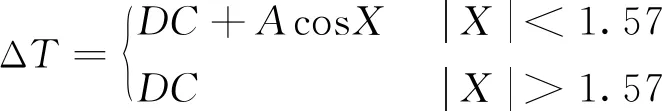
(15)

其中，ΔT为天顶方向电离层延迟误差(s)，DC为夜间天顶方向的时延(5ns)

(16)

(17)

(18)

其中，t′为地方时(卫星时/s)；φm为电离层星下点的地磁维度(°)；αn和βn由导航电文给定。

②任一时刻t，仰角为E的方向电离层延迟误差为

ΔT′=F·ΔT

(19)

其中，F表示倾斜因子

(20)

ΔT的适用公式为

(21)

2)电离层延迟误差模型相似度计算

由于不同仰角的电离层延迟可以通过相应的倾斜因子由天顶方向的延迟获得，所以这里只对天顶方向的电离层延迟误差模型进行相似度计算。基于地壳动力学数据信息系统(Crustal Dynamics Data Information System, CDDIS)所提供的实际数据，利用相似度法对Klobuchar电离层误差模型进行相似度计算。数据包括2018年3月份连续30d的电离层误差参数αn、βn和电离层的TEC map。TEC map所提供的数据范围为：经度(0°,360°)，纬度(-87.5°,87.5°)；分辨率为纬度相隔2.5°，经度相隔5°，以国际时为标准的时间相隔2h。广播模型的电离层延迟由参数αn和βn计算得到；而电离层延迟的实际值则由TEC map得到。

图5为同一时间、不同经纬度点的电离层模型相似度3D曲面。由图5可以看出，同一纬度所对应的不同经度点的模型相似度处于相同水平。

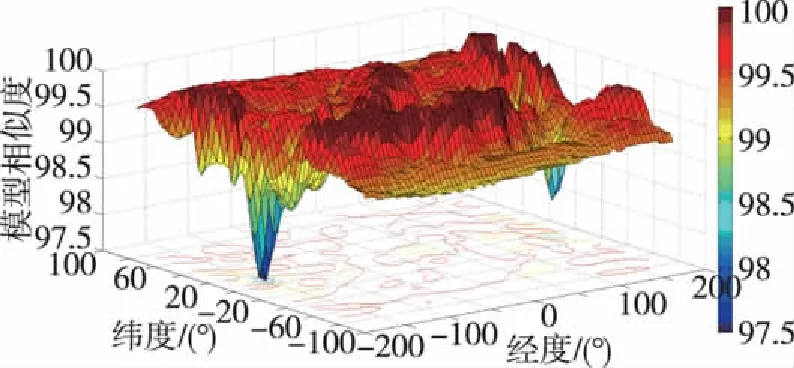
图5 不同经纬度位置点的模型相似度Fig.5 Similarity of model with different longitudes and latitudes

图6为图5中45°经度对应不同纬度的模型相似度。考虑到人类在南北极区域的活动较少，搭载接收机运动载体出现的概率较小，选取纬度±50°的范围进行电离层广播模型的相似度计算。在这一范围内，认为不同纬度对应的相似度权重取值相同，利用上述数据，最终得到电离层延迟的广播模型相似度r22为99.518%。

3.3.2 对流层延迟误差模型相似度计算

1)卫星对流层延迟误差

在卫星导航模拟器仿真系统应用时，对流层延迟对卫星信号产生的影响必须予以考虑。常用的卫星对流层延迟误差模型[10]有以下几种：Black模型、Hopfield模型、Saastamoinen模型及Egnos 模型。模拟器中使用的模型为Hopfield误差模型，该模型延迟是以测站温度、地面气压、观测仰角、水气压为变量的函数，其表达式如下

(22)

式中，E为仰角(°)，p0为地面气压(mbar)，Tk为测试站绝对温度，es为水气压(mbar)。

2)相似度计算

采用相似度法对Hopfield误差模型进行相似度计算。利用CDDIS网站所提供的从2018年3月1日0时0分开始，GPS观测站每隔5min实时采样所得的连续7d，共计2016个采样点的大气压、大气干分量温度、相对湿度数据，计算采样点对应的Hopfield模型的延迟结果。另外，CDDIS还提供了相应于气象元素采样点的标称误差小于4mm的精确对流层天顶方向延迟数据，这里作为实际对流层延迟，用来评估Hopfield对流层延迟模型的置信度。

图7所示为Hopfield模型一周内所有采样点对应的相似度，可以看出Hopfield模型与实际系统的相似度基本相当，该模型的精度较高。假设所有采样点的权重取值相同，最后得到Hopfield模型的相似度r23为99.62%。由此可见，Hopfield对流层误差模型的置信度水平较高。

3.3.3 卫星星历误差模型相似度计算

星历误差是卫星导航定位的重要误差来源之一，其大小取决于卫星跟踪测量站的个数与分布、观测值的精度与数量、卫星轨道模型以及测量定轨软件的优劣等。在卫星导航模拟器系统中，通常将卫星星历误差视为随机常值。即在进行模拟器单次仿真运行时，将卫星星历误差视为常值；而在进行多次仿真时，认为卫星星历误差服从零均值高斯分布

Δorbit～N(0,σorbit)

(23)

式中，Δorbit为卫星星历误差，σorbit为卫星星历误差在长时间范围内变化的标准差，通常取为2m。

国内外相关专家对卫星星历误差进行了深入研究，通过对卫星星历误差的大量研究与数据统计发现，在短时间内(不超过30min)，卫星星历误差是基本保持不变的；在长期范围内，卫星轨道误差的日平均值接近于0，日均方差基本保持不变。在卫星导航模拟器仿真系统中，通常设置模拟器仿真场景的时间不大于1d，在此时间段内将卫星星历误差视为零均值高斯分布，即所建立的卫星星历误差模型与实际模型比较一致，故这里将卫星星历误差模型的相似度r21估计为95.0%。

3.3.4 用户轨迹模型相似度计算

1)用户轨迹模型

以典型导航模拟器中抛物线用户轨迹为例，根据发动机和控制系统的工作状态，分为主动段和被动段，主动段运动相对复杂。根据载体受力分析，导航模拟器系统的运动方程可参考文献[11]。

2)模拟器仿真轨迹数据采集

设置模拟器抛物线的轨迹参数，包括开始位置、轨迹高度、轨迹首末直线距离、水平运动速度以及抛物线方位角。用户轨迹参数设置完成后，启动仿真并存储模拟器仿真输出的轨迹参数，以此作为原型系统。采用高精度卫星导航接收机采集并记录模拟器输出；选取轨迹参数包括直角坐标系3个方向的位置、速度、加速度以及加加速度作为相似元，即x、y、z、vx、vy、vz、ax、ay、az、jx、jy、jz。其中接收机加速度和加加速度为根据接收机采集的速度进行微分得到。

3)仿真轨迹模型相似度计算

以用户轨迹的vx相似元为例，首先，从实际的接收机采集数据中随机抽样一个容量为100的样本，与模拟器存储的同时刻仿真轨迹作差，并计算在置信度水平为0.95时样本均值的置信区间为[-0.2,0.2]，如图8中的红色实线段所示；然后，从用户轨迹模型的输出数据中随机抽样50个样本，并分别计算在置信度水平为0.95时每个样本均值的置信区间，如图8中的蓝色实线段所示。

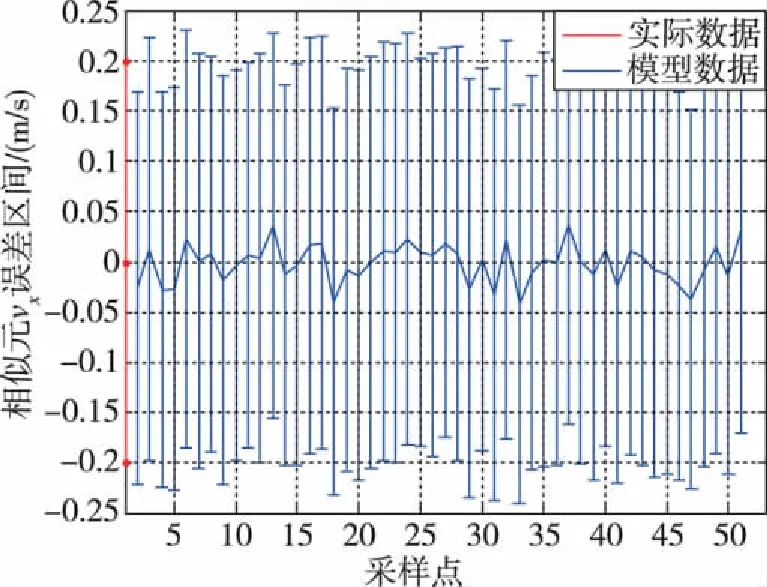
图8 模拟器用户轨迹vx的相似元误差置信区间Fig.8 Error confidence interval of similar elements for the speed vx of a simulated aircraft

同理，可求得其他相似元对应的相似值。故卫星导航模拟器用户轨迹模型各相似元对应的相似值为

SAR=[0.9754,0.9546,0.9432,0.9688,0.9622,

0.9701,0.8944,0.8932,0.8954,0.7933,

0.7933,0.7867]T

(24)

认为各个参数重要性是一致的，即认为各相似元的权重向量WAR为

WAR=[0.0833,0.0833,0.0833,0.0833,0.0833,

0.0833,0.0833,0.0833,0.0833,0.0833,

0.0833,0.0833]T

(25)

故卫星导航模拟器用户轨迹模型的相似度为

QAR=SAR·WAR=0.9022

(26)

即卫星导航模拟器用户轨迹模型的相似度r24为90.22%。可见，其用户轨迹模型的置信度较高。

3.3.5 其他底层子系统相似度计算

除以上4个关键指标外，其他底层指标特性包括时钟稳定性、时钟准确度、未调制的频谱纯度、未调制的频率相噪和谐波抑制。这些特性的共同特点是与时频或射频有关的硬件设计指标，即可以通过仪器直接或间接测量得到这些物理量，这些物理量为设计保证，直接决定了模拟的导航卫星信号质量。因此，针对这些子系统的相似度计算，可采用导航模拟器设计指标与真实卫星设计指标的比值作为该指标的相似度。即指标的相似度S可表示为

(27)

式中，i=1,…,N为该指标项目的N个分指标，Wi为第i个分指标的权重，Imi为模拟器的第i个分指标的指标要求或测量均值，Isi为真实卫星的第i个分指标的指标要求或测量均值，Ib为该指标的基准值，若无则置为0。通常，Imi≤Isi，若Imi>Isi则认为Imi=Isi。若无分指标，则认为Wi=1,N=1。

以未调制载波的频率相噪指标为例，模拟器技术说明中指标要求为：相位噪声(优于)：-70dBc/Hz@100Hz，-80dBc/Hz@1kHz，-85dBc/Hz@10kHz，-90dBc/Hz@100kHz；而卫星接口控制文件中的要求为相位噪声(优于)：-75dBc/Hz@100Hz，-80dBc/Hz@1kHz，-85dBc/Hz@10kHz，-95dBc/Hz@100kHz。认为各个带宽下相位噪声权重一致，则可以计算得到未调制载波的频率相噪的相似度r32为

(28)

同样，可以得到时钟稳定性、时钟准确度、未调制的频谱纯度和谐波抑制的相似度r11、r12、r31、r33分别为5.0%、99.9%、98.8%，97.5%。

3.4 卫星导航模拟器系统置信度综合评估

依据对数最小二乘模糊层次分析法得到的准则层权重向量，可计算得到一级模糊评估集Bi如下：

1) B1的一级模糊评估集为

2)B2的一级模糊评估集为

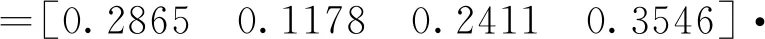
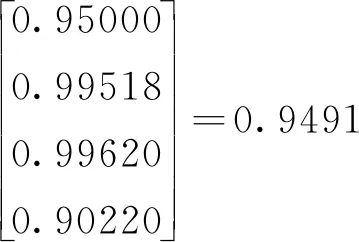
3) B3的一级模糊评估集为

=0.9776

将一级模糊评价结果构成二级单因素评判矩阵，得到综合评价向量为

=0.9235

从综合评价向量可以看出，卫星导航模拟器系统总体的置信度为92.35%，可见，卫星导航模拟器系统置信度较高。

4 结论

本文对卫星导航模拟器系统进行了置信度评估,提出了利用一种基于对数最小二乘的模糊层次分析法和相似度法相结合的置信度评估方案。首先，根据卫星导航模拟器系统的结构特点，建立了其置信度评估体系，将整个模拟器系统分解为若干仿真模型或子系统。方案利用基于对数最小二乘的模糊层次分析方法计算各个模型或子系统的权重向量，同时，使用相似度法给出模拟器系统的底层数学模型或子系统的置信度。然后利用计算得到的权重向量和模型或子系统的置信度逐级综合，得到卫星导航模拟器系统的总体置信度。该方案充分利用了对数最小二乘模糊层次分析法主观依赖性小的优点，并使用相似度法将复杂模型精准量化，科学有效，具有较高的工程使用价值。