考虑重力因素的离心式作动器运动控制仿真

王晓露，郭 鹏，冯立墨，赵鸿宇，聂振金

（北京精密机电控制设备研究所，北京，100076）

0 引 言

直升机在飞行过程中，始终承受着来自于旋翼、尾桨、发动机等机构的周期性振动力。高量级的振动载荷可以引起机体的高量级振动响应，不仅影响驾驶员与乘客的舒适程度和工作效率，而且会降低机体结构的疲劳寿命和可靠性，甚至干扰机载设备的正常工作[1～3]。

离心式作动器是一个可产生单向简谐振动力的装置。作为结构响应主动控制（Active Control Structure Response，ACSR）[4,5]的执行机构，可以通过控制产生与机体振动力相反的力，从而平衡机体振动，具有频带宽、输出力大、可靠性高、结构紧凑和所需功率小的优势。离心式作动器已逐渐成为国外先进直升机ACSR的主流配置[6,7]，中国尚处于理论研究和样机阶段[8,9]。从当前国内外公布的文献来看，文献[7]给出了重力矩计算公式但未进行详细研究，其他文献主要研究了稳态阶段的控制策略，多采用多项式速度规划模式[7～9]，尚未查阅到整个运行阶段详细划分的研究。当功率较大时，重力因素影响较小；但是作动器功率较小时，重力影响效应明显，需进行整个运行过程影响研究。因此，本文着重研究重力因素对作动器的性能影响和应对策略，为相关研究提供参考建议。

文章分析了一种采用两组同速反转质量块的结构布置方案的离心式作动器，考虑质量块重力矩影响，提出并开展了作动器启动、加速和控制3个阶段的控制算法及策略研究，最后基于Matlab/Simulink进行了运动仿真研究，对所提控制算法进行了仿真验证。

1 离心式作动器设计基础

1.1 机构工作原理

离心式作动器主要有四电机和双电机两种模式，采用2台电机驱动4个偏心轮的布置方案实现简谐振动力输出。三维原理模型与工作原理如图1所示，由两组（A和 B）同速反转的偏心轮机构组成，每个伺服电机驱动一组。

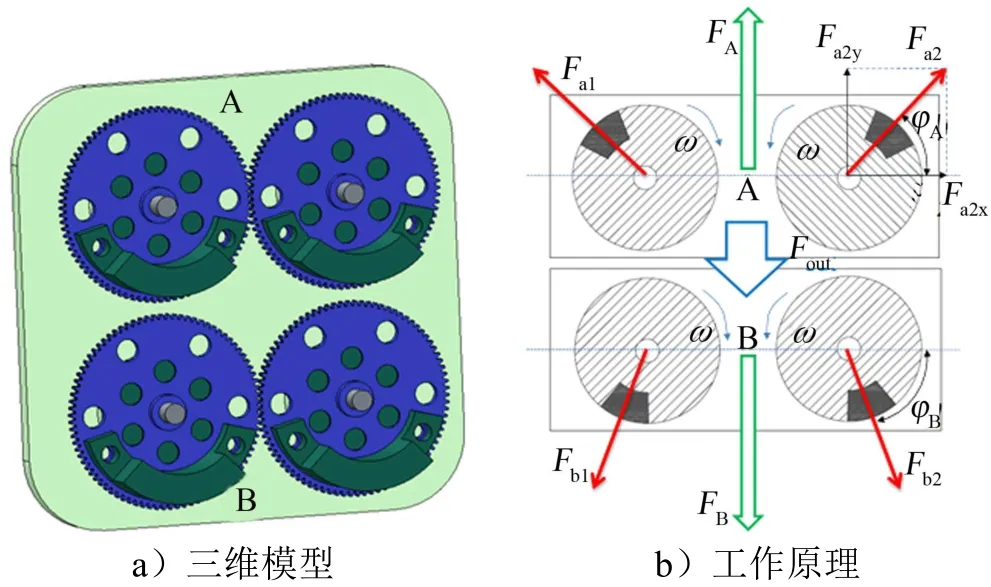
图1 离心式作动器Fig.1 Centrifugal Actuator

偏心轮的质量m、偏心距mr、转速ω决定离心力大小，同组偏心轮水平方向离心力分力相互抵消，仅对外产生垂直方向离心力分力。控制两组偏心轮旋转的相位差便可控制垂直方向离心力的矢量和，即可输出幅值、相位可调的振动力；控制偏心轮的稳态转速即可实现振动力频率调节。

A、B组偏心轮输出力大小为

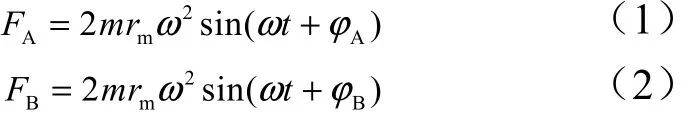
令Aϕθα=+，Bϕθα=−，即：

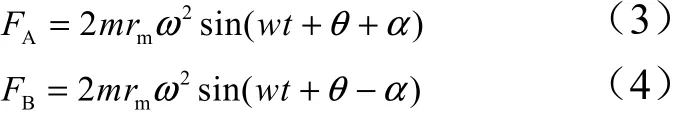
式中 θ为输出力的相位；α为A、B组偏心轮相位与输出力相位的差值。

联合式（3）、（4），求得输出力为

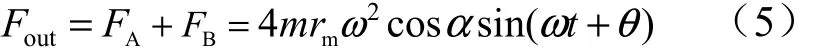
根据以上关系，得出如图2所示的输出力相位合成。

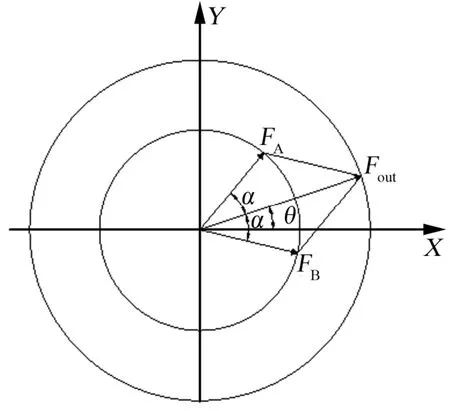
图2 离心式作动器输出力相位合成Fig.2 Phase Relation of Output Force for the Centrifugal Actuator

式（3）～（5）确定了离心式作动器输出力三要素（频率f，幅值Fout，相位θ）到A、B组机构控制参数ϕA/ϕB，ωA/ωB的解析关系。即：

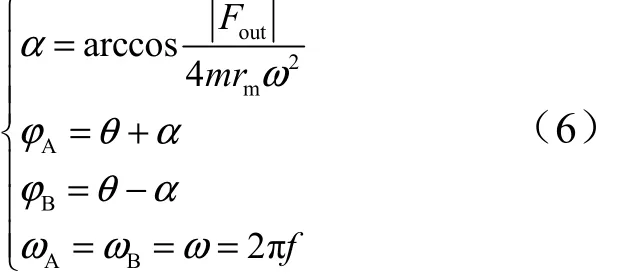
综上可知，作动器对外接受振动力指令信息，经过解算转换成偏心轮组的速度和相位的控制，相位控制采用速度轨迹规划的方式，通过加减速实现相位跟踪，并且保持一个稳态速度运行，具体的控制原理如图3所示。

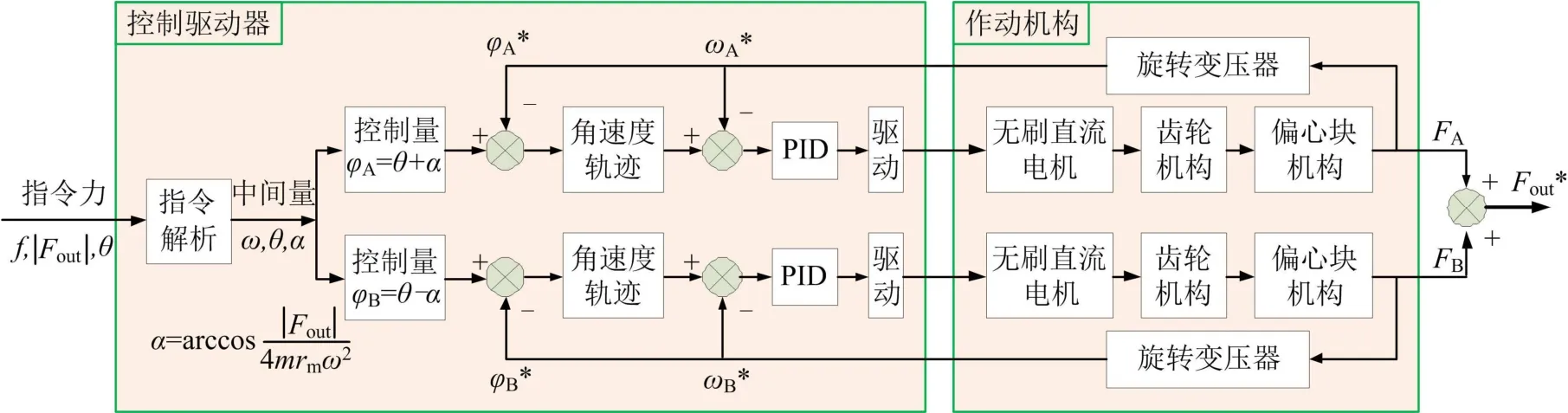
图3 离心式作动器控制框图Fig.3 Control Block Diagram of the Centrifugal Actuator

1.2 重力矩影响

以作动器输出力为重力方向为例，将一组偏心轮机构等效为一个旋转质子，得出考虑重力矩影响的作动器简化受力模型，如图4所示。

图4 重力矩影响下单组偏心轮机构的受力模型Fig.4 Simplified Force Model Considering the Gravity EffectMd—驱动力矩；ω—角速度；mg—重力；J—惯量； rm—偏心距；-Y—重力方向；ϕ-相位

不考虑摩擦力和驱动力矩情况下，计算重力矩造成的速度波动。假设偏心轮相位在0°时的速度为0ω，根据能量守恒定律有：

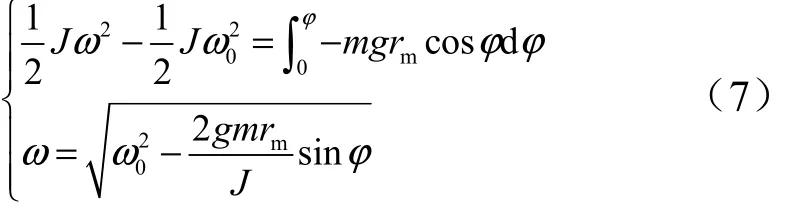
则作动器的系统固有速度波动为

不考虑摩擦力矩和驱动力矩，当偏心轮能量较大时可以进行着带有速度波动的连续旋转，并且随着0ω的增加，速度波动减小。离心式作动器稳态运行时，速度较高，且惯量大，所以速度波动较小，但是对于速度闭环控制而言，必须进行补偿从而避免不必要的能量消耗。

2 控制策略与算法研究

小功率模式下，作动器的输出力为重力方向或者输出力在重力方向分力比重较大时，质量块的重力矩成为一个不可忽略的因素。可能造成启机失败，并且速度波动会导致速度闭环在PID调节消耗能量巨大等问题。另外，离心机构具有较大的惯量，作动器启机到工作点需要时间，按照平滑加速曲线进行规划，可以避免速度超调引起的输出振动力过大。

综上分析，提出离心式作动器摇摆启动、正弦曲线加速、速度轨迹补偿控制3个工作阶段。

2.1 摇摆启动

如图4所示，如果质量块初始位置为-90°时，受电机功率和输出力矩影响，单向定压启动时，小功率模式下可能造成电机启动后在某个角度震荡，不限流的情况下可造成堵转从而烧毁电机。

考虑质量块的大惯量特性，具有飞轮储能效应，因此借鉴“秋千”原理，提出摇摆式启动方案，简易实现过程如下：

a）检测作动器转速和角度，当速度大于0时输入正电压，速度小于等于0时输入负电压，通过反复摆动加速，实现离心块能量累积。

b）当质量块达到一定的负角度时（该阈值与偏心轮质量特性和电机特性有关，且是宽范围），输入正电压，保证离心块转过顶点，从而实现持续旋转。

需要指出的是，功率较小时，可以通过摇摆启动解决；如果电机功率较大，并且力矩足够克服启动时的重力矩影响，则不采用摇摆启动。

2.2 正弦曲线加速

作动器正常启动后，存在从低速到稳态速度加速的过程。为了避免速度超调导致的输出力过大，并且兼顾快速性，采用1/4周期正弦曲线作为速度轨迹进行伺服控制。

正弦加速曲线公式为

式中sω，fω分别为加速段的初始和结束速度；st为加速段起始时间；λ为正弦曲线角频率；aT为加速段时间。正弦加速曲线的确定与电机的输出力矩（限定电流）直接相关。

2.3 指令控制过程

将离心作动器视为一个速度伺服系统，控制过程就是将控制指令转换成速度轨迹，通过速度跟踪完成相位控制，从而实现振动力指令控制。控制过程是指从当前稳定状态转变为指令状态的过程，参照图3流程，得出两组机构的相位和速度控制量，然后采用 5次多项式速度轨迹[9,10]进行控制，即：

由式（10）可知，确定控制周期 T和相应的输出轴相位差ϕ∆即可确定速度轨迹曲线。T和ϕ∆与电机功率的确定直接相关，是作动器设计的核心参数。

由于作动器是一个速度轨迹跟踪的伺服系统，考虑到离心式作动器重力矩引起的固有速度波动，在速度伺服控制闭环的速度输入处进行速度补偿，即：

式中 ϕ为偏心轮相位；c为补偿系数。作动器姿态和直升机姿态的影响计入补偿系数中。

3 仿真验证

3.1 仿真实现与框图

针对作动器运行过程进行全过程运动仿真研究，基于Matlab/Simulink进行了仿真框图构建，如图5所示，主要包含离心机构模型、速度规划模块、采样和指令模块等。

图5 离心作动器Matlab/Simulink仿真框图Fig.5 Simulation Block Diagram of Centrifugal Actuator Using Matlab/Simulink

单组离心机构模型包含电机模型、减速器、负载、与机构转角相关的重力矩、PID速度闭环等，从而构建成一个受重力矩影响的大惯量离心机构模型；速度规划模块主要包含多个速度轨迹生成模块，主要用于加速和控制阶段的速度轨迹生成；采样和指令切换模块主要用于设定采样控制时间和定时控制力指令的切换；其他相关模块有倾角设置模块、数据合成与显示模块等。

3.2 仿真结果

根据系统模型的特性，按照摇摆启动1.5 s、正弦加速2.5 s的仿真设置进行重力矩影响下的运动仿真，得出如图6所示的单组偏心轮的速度曲线。在摇摆启动阶段0～1.5 s内，偏心轮通过摆动积聚能量进行加速，最后越过顶点按照正向速度进行旋转；在1.5～4 s加速阶段内，为了平抑固有的速度波动，偏心轮跟踪速度补偿轨迹进行伺服控制，结果显示机构按照正弦加速曲线实现了稳定加速。A组机构的电流消耗如图7所示。摇摆启动段按照最大限流进行驱动，加速段初始阶段加速度较大，耗能高，随着速度提升，加速度降低，机构平滑加速至工作速度。验证了第 2.1、第2.2节的方法和理论。

图6 重力矩影响下的离心作动器启动/加速过程Fig.6 Starting and Accelerating Process Considering the Gravity Effect for the Centrifugal Actuator

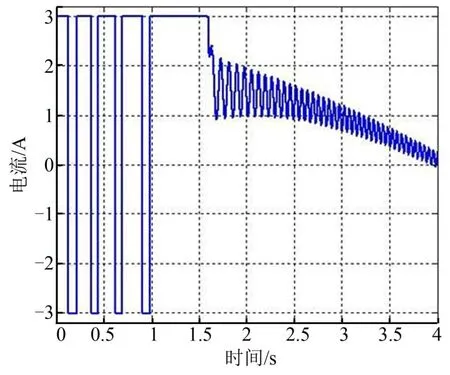
图7 启动/加速过程电流消耗Fig.7 Current Consumption for Starting and Accelerating Process

重力矩造成的速度波动是作动器的固有特性，但是依靠电机的输出力矩保证作动器速度平稳需要较大的功率输出。在不影响抑振效果的基础上，降低作动器功率消耗是优先选项，按照第2.3节的速度轨迹生成和速度补偿方法，以两个实例进行仿真验证：a）35 s处输出力相位跟踪；b）40 s处输出力幅值跟踪。仿真结果如图8所示。

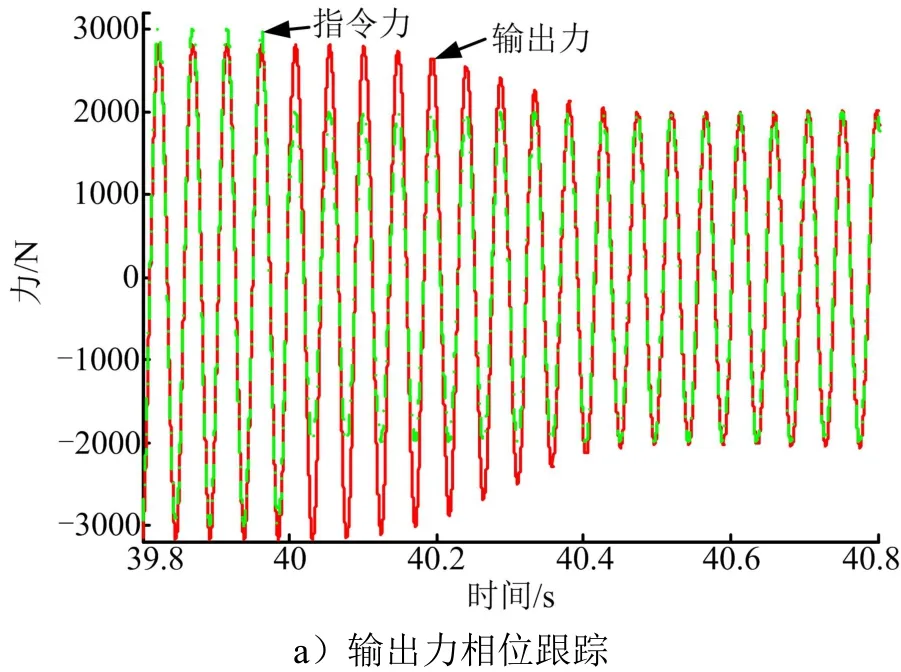
图8 控制过程仿真示例Fig.8 Example of a Control Process

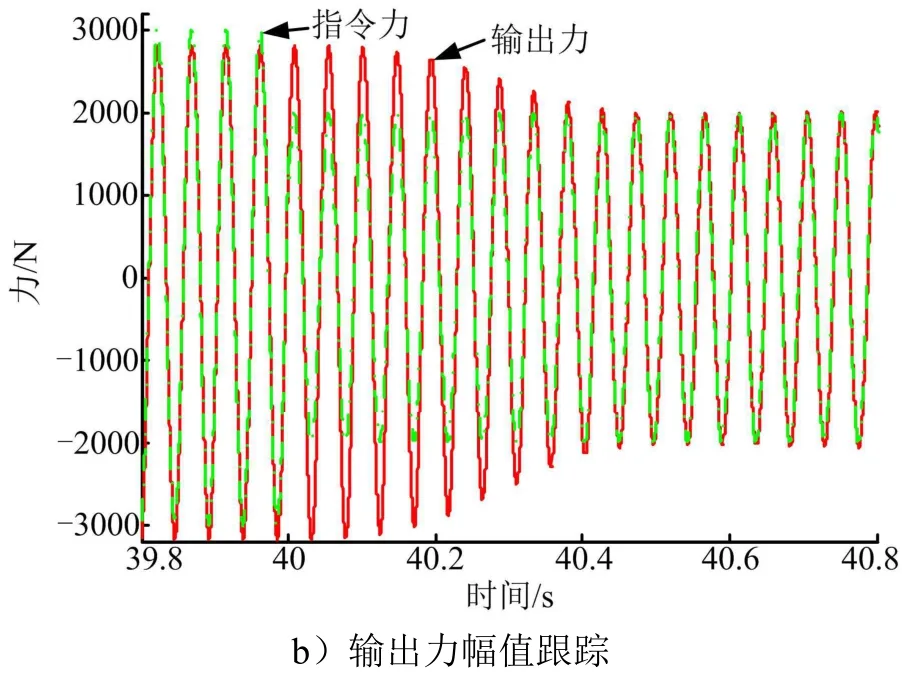
续图8

从图8a可以看出，输出力在0.5 s的时间内完成了相位跟踪；从图8b可以看出，输出力在0.5 s的时间内完成了幅值跟踪，并且相位保持了一致，验证了控制过程算法的正确性。

相比于直接采样速度进行闭环的方式，采用速度补偿的控制方式消耗的电流更小，上面两个仿真示例的电流消耗对比曲线如图9所示。

图9 电流消耗对比Fig.9 Comparison of Current Consumption

由图9可以看出，直接控制方式基本以最大电流去控制电机，而速度补偿控制方式将重力引起的固有速度波动考虑在内，顺势而为，避免了不必要的速度剧烈调节过程，大大降低了系统能耗。

4 结 论

考虑重力矩影响，解决了离心式作动器分阶段运行和控制阶段直接控制的高能耗问题。但是重力因素导致的输出力误差目前仍然存在，表现为顶点速度低和底部速度高，导致正、反向输出力不一致，这是系统的固有特性。

因此，即使采用速度补偿式控制方案，也会不可避免地出现重力方向输出力误差。如何进一步利用系统的固有特性，在离心机构的旋转周期内进行速度和电流综合，以速度平稳性和能耗量为目标进行控制律的优化设计，是后续值得研究的问题。考虑两组电机及其传动机构固有性能的不一致性，如何通过双电机协同控制实现更好性能，需要进一步探索研究。

本次研究中完成了可输出单向简谐振动力的离心式作动器设计；以重力矩影响为切入点，提出并仿真验证了离心作动器启动、加速和控制 3个运行阶段，为中国离心式作动器的研究提供了进一步参考；借鉴“秋千原理”提出了摇摆启动方法，采用正弦曲线实现了平滑加速过程，基于多项式速度轨迹和补偿方法实现了指令控制并解决了高能耗问题，这些方法和理论适用于重力矩影响较大的离心式作动器。