V-型皱褶芯材一体化热防护结构等效热传导系数预测

周 晨，王志瑾，候天骄

（1. 南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京，210016；2. 南京航空航天大学航天学院，南京，210016）

0 引 言

无论是弹道式再入飞行器还是高超声速巡航飞行器，当其在大气中高速飞行时都将面临严峻的气动加热环境。热防护系统最主要的功能是保证飞行器机体结构及内部设备、人员在各种飞行条件下的工作环境温度在许可范围之内[1]。而防热-结构一体化热防护系统将高超声速飞行器的机体结构设计与热防护设计相结合，使得热防护结构既能承受飞行过程中可能遇到的各种机械载荷，同时又具备良好的防热性能[2,3]。

夹层结构比强度、比刚度高，抗冲击性能好，隔热性能优异，利于实现防热-结构一体化设计[4]。皱褶芯材作为一种新型芯材，其成型工艺简单，几何设计性好，且作为夹层结构的芯材与上、下面板构成开环空腔，在隔热、隔音、吸能等诸多方面有着广阔的应用前景[5,6]。王志瑾等[7]采用实验和数值模拟的方法研究了铝合金皱褶芯材夹层板的当量导热系数，并分析了相关几何参数对当量导热系数的影响；周华志等[8]采用数值方法对皱褶芯材几何参数对结构吸能性能的影响进行了分析和优化；欧洲多国联合开展的CELPACT项目[9]将皱褶芯材夹层结构列为重点研究结构型式，对其力学性能和抗冲击性能进行了系统的研究；Fischer[5]和Heimbs[10]等对压缩、剪切和冲击载荷作用下的皱褶芯材夹层板进行了一系列数值模拟和实验研究；Blosser等[11]对不同形式的热防护结构的研究表明，一维传热模型可以有效地预测结构沿厚度方向的温度变化。

因此，在热防护结构设计与优化的初始阶段，有必要建立结构的一维等效传热模型，从而减少计算量。本文对V-型皱褶芯材一体化热防护结构进行了一维传热等效，给出了计算等效热传导系数的修正混合定律；对基于三维稳态传热分析得到的等效热传导系数与修正混合定律的计算结果进了对比；分别对三维模型和一维模型进行了典型再入环境下的瞬态传热分析，并对比了沿结构厚度方向各点的温度-时间响应。

1 皱褶芯材一体化热防护结构

1.1 模型描述

皱褶芯材是将平板基材按照一定规律的线系网格进行局部折叠而得到的一种具有周期性胞元构型的三维立体芯材。而皱褶芯材一体化热防护结构充分利用了皱褶芯材夹层结构中芯材与上、下面板之间的空腔，在其中填充轻质隔热材料，如图1所示。其中，皱褶芯材与隔热材料共同组成了中间层。承力结构由上、下面板及芯材构成，同时上面板充当了热结构的角色，并辐射掉大部分的热量，由于中间隔热层的存在，只有少量热量到达下面板，从而保证机体内部温度在许可范围之内。图2为典型的V-型皱褶芯材胞元构型及其几何尺寸示意，其中图2a所示的胞元构型可由图2b所示的由周期排列的平行四边形平板折叠而成。V-型皱褶芯材胞元可由芯材高度 H、锯齿形线步长 2L、Z型线步长2S以及Z型线的折幅W 4个独立的参数表示[12]，并与平面基板上所对应的线系几何参数有如下关系[13]：

式中0L和0S分别为平面基板上 Z型线的间距和步长；0W为平面基板上Z型线的折幅。

图1 V-型皱褶芯材ITPS结构示意Fig.1 A Typical V-pattern Folded Core ITPS Structure

图2 典型V-型皱褶芯材胞元示意Fig.2 Illustration of a Typical V-pattern Folded Core Unit Cell

1.2 材料属性

参考波纹芯材夹层板式一体化热防护结构各部分的材料选择[4]，上面板采用耐高温的镍基合金 Inconel 718，皱褶芯材采用钛合金 Ti-6Al-4V，下面板则采用铝合金Al 2024-T851，隔热材料选用密度ρ为48 kg/m3的SAFFIL[14]，相关材料属性见表1，其中考虑了材料热传导系数 k与比热 c随温度的变化[15]，具体关系曲线如图3所示。

表1 材料热物理属性Tab.1 Material Thermal Physical Properties

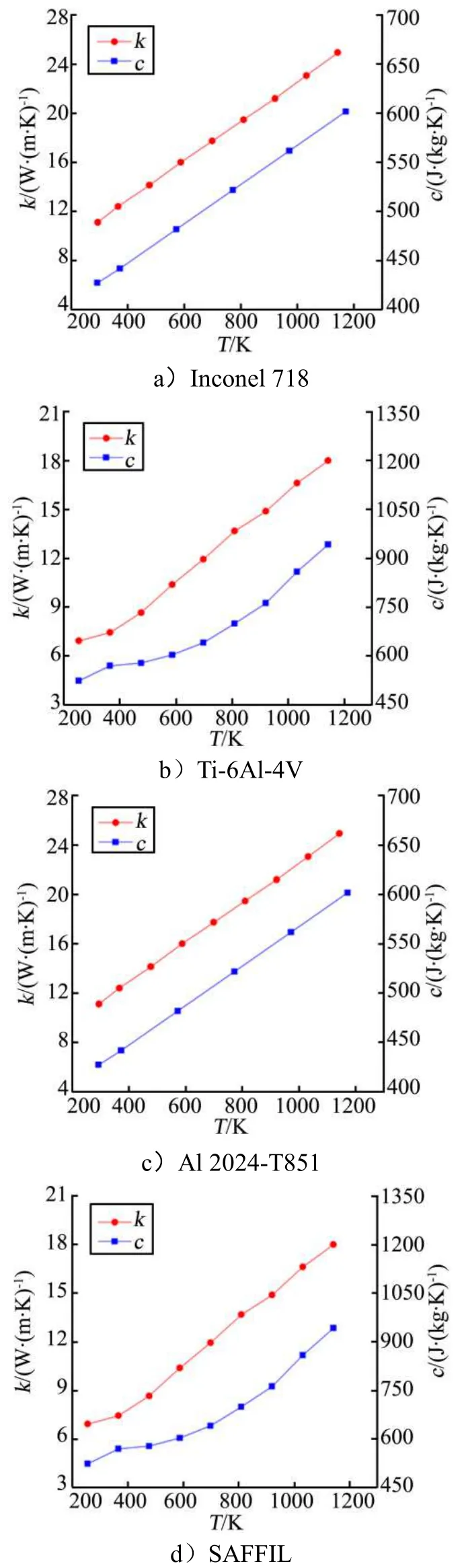
图3 材料热物理属性随温度变化曲线Fig.3 Material Thermal Physical Properties Variation with Temperature

2 V-型皱褶芯材等效热传导系数

根据图2所示V-型皱褶芯材胞元及其线系规律可知，夹角φ的最小值理论上可无限趋近于0°；最大值可达到90°，此时W=0，芯材沿Z向的折线退化为一条直线。夹角φ可由4个独立的几何参数通过下式表达：

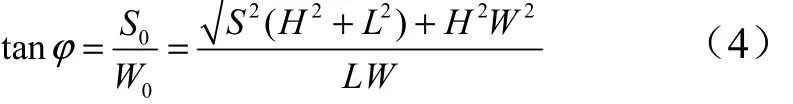
由于下文在推导中间层等效热传导系数时将更多的采用sin φ的形式，因此这里先将其表示为

根据皱褶芯材固有的周期性特点，假设相邻两个胞元之间没有热量传递，因此只需对一个胞元进行分析。由于胞元存在一个对称面，为了减少计算量，这里取半个胞元作为研究对象，沿结构厚度方向（Y向）的传热简化过程如图4所示。

图4 V-型皱褶芯材一维传热模型简化Fig.4 Simplification of the 1-D Heat Transfer Model of the V-pattern Folded Core

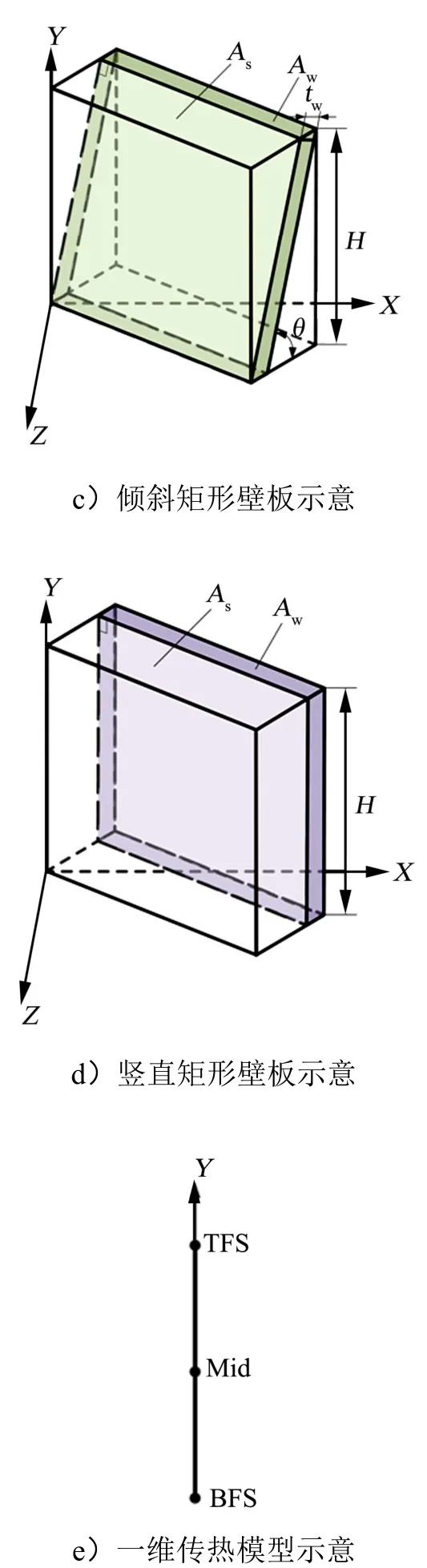
续图4

在材料科学领域，常采用加权平均方法来预测复合材料的各种材料属性，这种方法称为混合定律。针对由V-型皱褶芯材与隔热材料组成的中间层，若采用通常的基于体积平均的混合定律，其等效热传导系数ke可表示为

式中 kw，ks分别为V-型皱褶芯材壁板与隔热材料的热传导系数；分别为两者各自所占胞元的体积分数。

式中 tw为芯材壁板的厚度，如图4b所示。

然而，式（6）忽略了芯材壁板形状以及壁板位置的影响，直接采用该表达式进行等效热传导系数预测将造成较大的误差。因此，需引入芯材壁板的形状参数和位置参数对混合定律进行修正。由于隔热材料的热传导系数很小，故忽略胞元中隔热材料的形状与位置对ke的影响。为了简化分析过程，在从图4b向图4d的简化过程中，暂时只考虑芯材壁板的传热。首先，考虑芯材壁板形状的影响，将平行四边形芯材壁板（图 4b）转化为与之具有相同夹角 θ的矩形壁板（图4c）。为了使两者具有相同的传热效果，两者需满足以下关系：

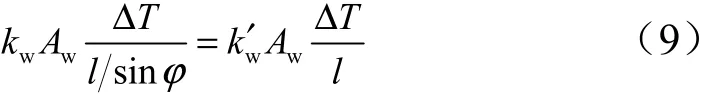
式中wk′为图4c中壁板的热传导系数；Aw为芯材壁板沿Y向的横截面积。

根据式（9）可得：

随后，再考虑芯材壁板位置的影响，将与上、下面板呈夹角θ的矩形壁板（图4c）转化为与面板垂直的矩形壁板（图4d）。同理可得以下关系式：

式中wk′′为图4d中壁板的热传导系数。夹角θ与夹角ϕ之间存在以下关系：

根据式（11）可得：

最后，对图4d所示的中间层模型采用混合定律可得到中间层等效热传导系数：

等效密度 ρe与等效比热ce则可分别采用基于体积加权平均和基于质量加权平均的混合定律直接得到：

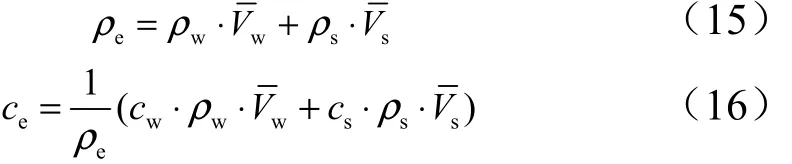
式中 ρw，ρs分别为芯材壁板与隔热材料的密度；cw，cs分别为两者的比热。

综上所述，V-型皱褶芯材一体化热防护结构沿其厚度方向的传热可简化为如图4e所示的一维模型，中间层的等效热物理属性则可由式（14）～（16）得到。

3 验证与分析

3.1 数值模型分析验证

为了评估经上述修正后的混合定律计算所得到的等效热传导系数的精度，采用Abaqus有限元分析软件建立 V-型皱褶芯材一体化热防护结构的详细三维模型，并对其进行稳态传热分析。三维传热模型如图5a所示，其中图5b为隐藏了隔热材料之后的结构面板和芯材。

采用三维实体单元DC3D8进行网格划分，经过网格收敛性分析后，最终选用的网格划分方案单元总数为9800，节点总数为12 105。对上、下面板分别施加400 K和300 K的恒定温度载荷，其余壁面均作绝热处理。为了便于对比，在稳态传热中假设材料属性不随温度变化，这里取温度约为350 K时所对应的值。

图5 三维传热模型示意Fig.5 Illustration of the Detailed 3-D Heat Transfer Model

根据傅里叶定律，整个夹层板的等效热传导系数可表示为

式中 q为沿夹层板厚度方向，即Y方向的平均热流密度，由于皱褶芯材壁板与隔热材料热物理属性的差异，热流密度在 X-Z平面内并不是均匀分布的，平均热流密度可由下式得到：

式中 n为X-Z平面内的单元数；Ai为该平面内第i个单元的面积；qi为第i个单元的平均热流密度。

为了得到平均热流密度q，采用关键字*SECTION PRINT将下面板下表面BFS-Bot的总热流及其面积输出到相应的dat文件中。在Abaqus提交分析任务之前，打开Model ＞ Edit Keywords对话框，在Output区域插入以下关键字：

*SECTION PRINT, name=botface, surface=BFS-Bot,freq=1

SOH, SOAREA

其中，SOH表示返回总热流，SOAREA表示返回总面积，分别与式（18）中的分子和分母相对应，从而可计算得到平均热流密度q。

在得到整个夹层板的等效热传导系数后，再根据多层平壁稳态传热的热阻网络即可得到皱褶芯材与隔热材料组成的中间层的等效热传导系数为

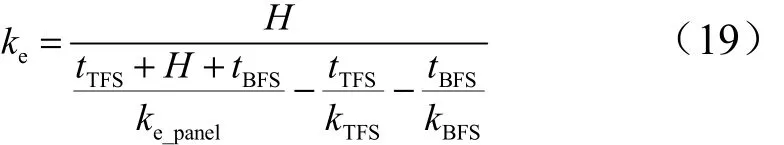
式中 tTFS，tBFS分别表示上、下面板的厚度；H为中间层的厚度。

由于皱褶芯材几何设计参数较多，为了保证修正后的混合定律在整个设计空间中的适用性，采用拉丁超立方抽样方法对如表2所示的设计空间进行抽样，得到30组样本点。上、下面板厚度则取定值2 mm。

表2 设计变量变化范围Tab.2 Ranges of Design Variables

采用修正混合定律对各样本点的等效热传导系数进行预测，并与由上述详细三维模型计算所得结果进行比较。计算结果表明，在整个样本空间中，最大相对误差不超过4%。误差分析如图6所示，横、纵坐标分别为修正混合定律和三维有限元传热模型所对应的等效热传导系数值，对角线表示两者结果完全相同，由圆点代表的样本点越接近黑色对角线表示两者结果接近程度越高。从图6中可以看出两者结果非常接近，表明利用修正混合定律来预测中间层的等效热传导系数具有较高的精度。

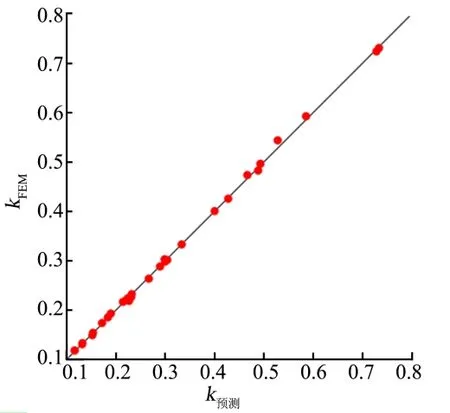
图6 误差分析Fig.6 Error Analyses

3.2 瞬态传热分析

为了进一步检验采用等效热传导系数的一维传热模型在热防护结构设计和优化过程中的适用性，对典型再入环境下V-型皱褶芯材一体化热防护结构的详细三维模型和简化一维模型分别进行瞬态传热分析。其中三维模型与稳态传热中所采用的模型一致。简化一维模型则采用DC1D2二节点杆单元，并进行网格收敛性分析，最终确定模型单元总数为20，节点总数为21。中间层采用根据修正混合定律计算得到的等效热物理属性。由于再入过程中气动加热严重，结构温度变化较大，因此需考虑材料属性随温度的变化（表1和图3）。参考再入过程中可重复使用飞行器机腹位置的热载荷[4]，对上面板外表面施加图7所示的热流密度，下面板采用偏保守的绝热边界条件。同时，考虑上面板与周围环境的辐射换热以及当热流密度减小到零时上面板与周围环境的对流换热。假设结构初始温度与周围环境温度均为295 K，辐射率为0.86，表面对流换热系数为 6.5 W/(m2·K)[4]。

首先，利用简化一维模型对结构进行瞬态传热优化，约束条件为整个时间历程内下面板的最大温度，目标函数为结构面密度。皱褶芯材几何参数变化范围如表2所示。同时，考虑上、下面板厚度的变化，其取值范围与芯材壁板厚度一致。优化问题描述如下：

式中 ρ*和ρ分别为结构面密度和各部分的体积密度；Tbotmax为下面板最大温度值。

表3给出了优化前后皱褶芯材和面板的几何参数取值以及相应的约束和目标函数值。从表3可以看出，在上述载荷及边界条件下，当约束条件仅考虑下面板温度时，优化后的结构退化为波纹板构型（W=0 mm）。

表3 瞬态传热优化结果Tab.3 Transient Heat Transfer Optimization Results

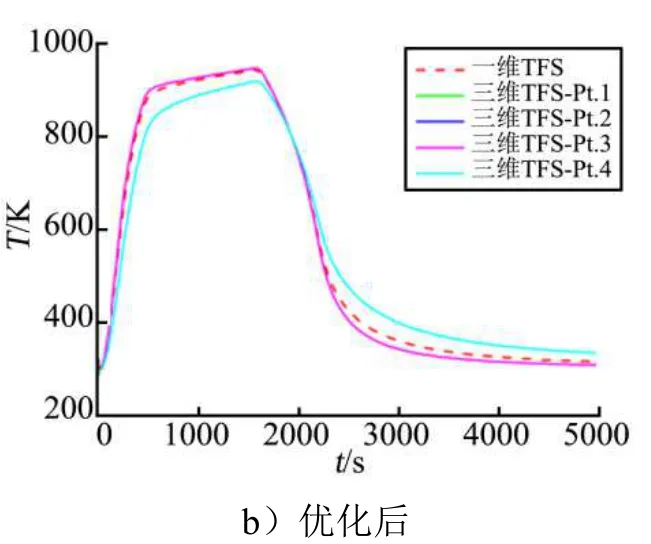
针对表3中的两种参数组合分别进行一维和三维瞬态传热分析，在结构上、下面板和芯材中选取若干监测点（图4e和图5b）并得到各点在整个再入过程中的温度响应。图8至图10分别为两种结构的上面板、芯材中部及下面板所对应的温度随再入时间的变化曲线，其中实线为三维模型的结果，虚线为一维模型的结果。

图8 上面板温度-时间变化曲线Fig.8 Temperature Variation with Re-entry Time at TFS

续图8

图9 芯材中部温度-时间变化曲线Fig.9 Temperature Variation with Re-entry Time at Mid

图10 下面板温度-时间变化曲线Fig.10 Temperature Variation with Re-entry Time at BFS

续图10

从图8可以看出，一维模型能够较精确地预测上面板的温度变化，其温度-时间曲线大致处于三维模型4个监测点所对应的曲线中间。图9为芯材中部的温度响应，从图9a可以看出，当热流密度达到最大时，三维模型中两个监测点之间的温度差异最大，同时2种模型之间的偏差也较大，这主要是由皱褶芯材壁板呈平行四边形的特征所导致的。由于一维模型的预测结果大致位于三维分析结果的中间，且正确地反应了该位置的温度变化趋势，在结构的初始设计阶段仍具有重要的参考价值。同时，随着W值的减小，芯材壁板形状由平行四边形逐渐趋向矩形，各个位置沿 Z向的温度分布趋于均匀，如图9b所示，一维模型能够较精确地预测该位置的温度变化。图10为下面板的温度变化曲线。下面板的温度通常作为热防护结构设计中的一个重要指标，其值的准确性尤为重要。从图10中可以看出，由于中间隔热层的存在，下面板温度分布的不均匀程度大大降低，三维模型中的四个监测点结果几乎重合，而一维预测结果也与三维计算结果非常接近，针对优化前后的两种不同几何参数组合，预测相对误差均在2%以内。

由上述结果可以得出，采用基于修正混合定律的简化一维模型能够正确反映结构沿厚度方向各点的温度变化，与三维传热模型相比，其在有效提高计算速度的同时又不失精度要求，可有效应用于V-型皱褶芯材一体化热防护结构的设计与优化。

4 结 论

a）针对一种基于V-型皱褶芯材的一体化热防护结构进行了沿结构厚度方向的一维传热等效，给出了用于计算等效热传导系数的修正混合定律。

b）建立了结构的详细三维传热模型，采用数值计算方法得到结构的等效热传导系数，与修正混合定律的计算结果进行对比，验证了修正混合定律的精确性和适用性。

c）通过对三维模型和一维模型在典型再入热载荷下的瞬态传热分析与对比，表明一维等效模型可以较准确地预测沿结构厚度方向各点的温度响应。

d）将基于修正混合定律的一维等效传热模型应用于V-型皱褶芯材一体化热防护结构的初步设计与优化中，可有效节约时间成本，提高计算效率。