基于落速预测理论的子母弹抛撒高度优化算法
刘 赛,李长春,朱 敏,李宇鹏,熊学文
(北京航天长征飞行器研究所,北京,100076)
0 引 言
导弹是现代战争中的主要兵器之一,子母战斗部由于其能够有效扩大针对目标的覆盖面积,在导弹武器发展中得到了广泛的应用,如果按照目标特性和毁伤效果对子母弹系统进行优化设计,则能够大幅提高子母战斗部的毁伤效能。
子母战斗部最终的毁伤效能由子弹数量、威力及其落点分布决定。子弹的落点分布主要取决于母弹的弹道参数特性、子弹的气动特性、子母弹抛撒特性和子弹的抛撒高度等因素。文献[1]和文献[2]均对子母弹的抛撒半径优化技术进行了研究,其研究成果均可作为子母弹抛撒半径的优化设计方法;文献[3]和文献[4]对子母弹开舱高度的高低散布因素进行了分析,提出了敏感参数和敏感度的概念。可见对于子母弹,抛撒半径是一个非常重要的战术技术指标,针对抛撒半径开展优化分析工作也是研究的热点。
本文首先对子弹飞行弹道进行建模,然后根据落速预测的理论对母弹飞行至理论抛撒高度时的速度进行预测,并设计了一种重新计算抛撒高度的算法,根据该算法的计算结果在空中重新装订抛撒高度,通过仿真计算结果统计,应用该方法后的子母弹抛撒半径误差将明显减小。
1 动力学建模
导弹抛撒子弹时已经进入导弹的飞行末段,通常此时的飞行高度较低,在研究子母弹抛撒技术时,可以把地球看作其圆球模型与抛撒时母弹海平面高度弹下点相切的平面大地,在大地平面中建立抛撒点当地坐标系,如图1所示。

图1 子弹抛撒坐标系、抛撒半径定义Fig.1 Definition of Dispersion Coordinate System and Dispersion Radiusr—抛撒半径
原点O为上述的切点,Oy轴垂直于大地平面指向母弹的抛撒点,Ox轴在平面内指向母弹速度矢量在平面投影的方向(若速度方向垂直于平面,则可以任意选择x轴方向),Oz轴按右手定则确定。
把母弹和子弹视为稳定的质点,在抛撒点当地坐标系中建立子弹的飞行动力学和运动学方程:

式中 x,y,z为子弹在抛撒点当地坐标系中的坐标;Vx, Vy, Vz为子弹速度矢量在抛撒点当地坐标系中各轴上的投影;V为子弹相对抛撒点当地坐标系的速度;m为子弹的质量; CA为子弹轴向力气动系数即阻力系数;q为动压;ρ为大气密度; g0为重力加速度,考虑导弹抛撒高度高度通常在5 km以下,重力加速度变化较小,为简化公式推导,取为海平面重力加速度,9.806 65 m/s2。
对式(1)进行数值积分,可以计算出子弹的落点。在计算子弹落点的抛撒半径时,可以简化计算前、后、左、右4枚子弹的落点,然后根据落点坐标计算等效圆半径。在计算不同落点子弹的积分初始条件中,子弹的位置坐标相同即母弹的位置:

式中0h为母弹在抛撒点的高度。
各子弹的初始速度不同,前落点子弹初始速度为

式中0V为母弹在抛撒点相对抛撒点当地坐标系的速度;0ϑ为母弹在抛撒点的当地弹道倾角;pV为抛撒子弹的最大速度。
后落点子弹初始速度:
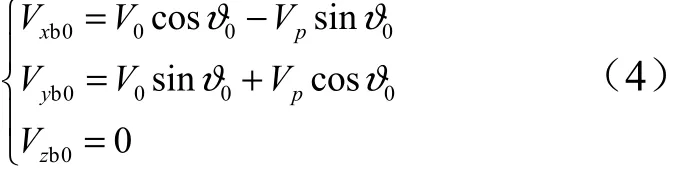
左落点子弹初始速度:

右落点子弹初始速度:

以式(2)~(6)为初始条件,对式(1)进行数值积分,计算得到子弹的前、后、左、右落点,坐标分别为:,其中 hc为落点高程,m。
计算抛撒半径r:
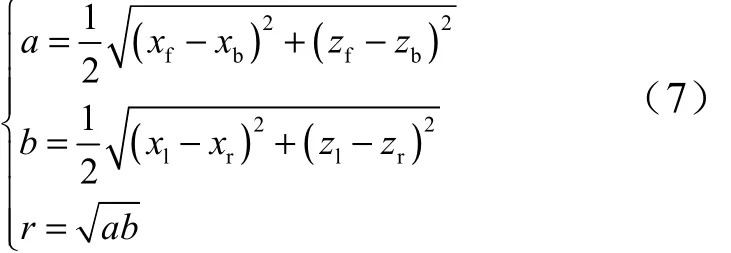
2 落速预测理论
通常情况下,很难得到母弹飞行动力学的解析解,但是当母弹在距离目标较近的情况下,通过以下一系列假设,有利于得到落速解析解:
a)因母弹离目标较近,可以只考虑俯仰平面飞行器的动力学方程;
b)母弹的当地弹道倾角变化范围较小;
c)母弹落速的马赫数在较小的变化区间中,且不涵盖亚跨声速范围,母弹阻力系数 Cx取常值(可以根据经验进行适当修正);
d)母弹抛撒前攻角近似为0;
根据以上假设,得到再入飞行器运动的动力学方程[7]:
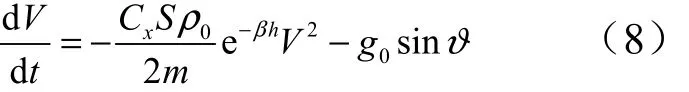
对式(8)进行变量替换,可得:

式中eV为进行预测时母弹的速度;eh为进行预测时母弹的高度。
使用式(9)计算时,可以根据需要保留不同阶数,在本文的计算中,保留二阶。
3 抛撒高度优化算法
综合式(1)~(7)可得:

根据式(10)的全微分可以近似得到[8]:

式中 Re为抛撒半径;∆Re为抛撒半径偏差。
在导弹方案已经确定的情况下,在飞行末段抛撒参数ϑ0和Vp很难通过主动控制改变,因此可以认为在式(11)中,∆ϑ0=0,∆Vpmax= 0 ,式(11)简化为如下形式:
如果导弹仍在原理论高度进行抛撒,即00h∆=,可以得到:

根据式(9),即可求出导弹在原理论高度的速度与理论速度的偏差0V∆,从而根据式(13)求出导弹在原理论高度抛撒时的抛撒半径偏差eR∆。本文设计一种空中装订抛撒高度的算法,计算导弹需要调整的抛撒高度,将该高度装订至导弹的引爆控制系统中,导弹将根据新装订的高度进行抛撒,以抵消式(13)的偏差,从而减小抛撒半径的误差带。
根据式(12)可以近似得到:

其中,可以根据式(9),以0V和0h替换式(9)中的V

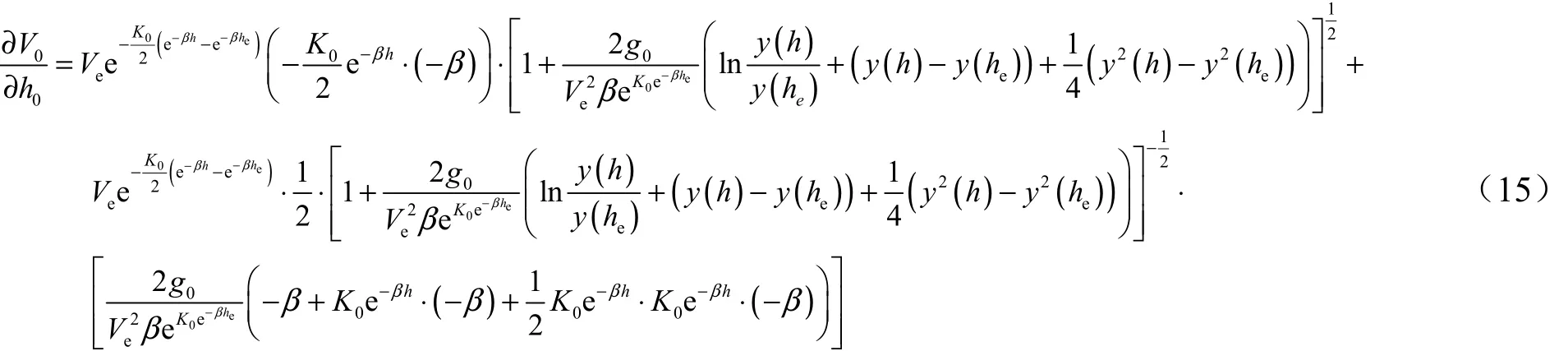
根据式(13)、式(14),为抵消由抛撒点速度偏差0V∆带来的抛撒半径偏差,可以得到:

整理式(16),得到:

式中 ∆h0为在原抛撒高度基础上需要调整的高度;∆ V0为根据式(9)预测的速度与导弹理论速度的差(均在原理论抛撒高度上)。
将式(15)的计算结果代入式(17),即可得到导弹需要调整的抛撒高度。
4 仿真计算
根据上文的算法计算1个算例:
假设导弹最大抛撒速度为40 m/s,设计抛撒高度为2000 m,抛撒时母弹速度为1000 m/s,抛撒时母弹当地弹道倾角为-60°,当母弹飞行至5000 m时进行落速预测并装订优化后的抛撒高度。
初始条件代入式(1)~(6),计算得到抛撒半径为96.9 m。抛撒半径对抛散参数的偏导数如表1所示。

表1 偏导数计算结果Tab.1 Computational Results of Partial Derivatives
考虑母弹质量、母弹速度、母弹当地弹道倾角、母弹气动力系数、子弹质量、子弹气动力系数和大气密度等偏差,应用Monte Carlo法打靶计算1000条弹道,统计按理论高度抛撒的抛撒半径结果和按算法装订抛撒高度的抛撒半径结果。
母弹和子弹抛撒参数和特性参数的误差如表2所示。

表2 抛撒参数和特性参数的误差Tab.2 Errors of Dispersion Parameters and Characteristic Parameters
统计结果如表3所示。

表3 抛撒半径统计结果Tab.3 Statistical Result of Dispersion Radius
5 结 论
本文设计的优化算法简单,利于导弹在空中进行抛撒高度的计算装订,应用本算法后,可明显地减小子母弹抛撒半径的误差带,有益于精确控制子母弹的抛撒半径,从而实现最优的毁伤效果。
同时,子弹出舱后的抛撒姿态、子弹气动稳定性、母弹激波层等会为子弹带来飞行稳定性的影响,从而会影响子弹散布,对此本文未进行分析,这也将是后续研究的方向。但是,可以根据地面试验和飞行试验获取的数据对本文所述的方法进行修正,主要是修正母弹和子弹的阻力系数,修正后的方法仍可以适用于工程应用。

